Iterative technique for circular thin plates on Gibson elastic foundation using modified Vlasov model

Feng Yue, Ziyan Wu, Haifeng Yang, Mengying Li

School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi'an 710072, China

Keywords:Circular thin plate Gibson soil Modified Vlasov model Bendings Iterative technique

A B S T R A C T In this paper, to investigate the influence of soil inhomogeneity on the bending of circular thin plates on elastic foundations, the static problem of circular thin plates on Gibson elastic foundation is solved using an iterative method based on the modified Vlasov model. On the basis of the principle of minimum potential energy, the governing differential equations and boundary conditions for circular thin plates on modified Vlasov foundation considering the characteristics of Gibson soil are derived. The equations for the attenuation parameter in bending problem are also obtained, and the issue of unknown parameters being difficult to determine is solved using the iterative method. Numerical examples are analyzed and the results are in good agreement with those form other literatures. It proves that the method is practical and accurate. The inhomogeneity of modified Vlasov foundations has some influence on the deformation and internal force behavior of circular thin plates. The effects of various parameters on the bending of circular plates and characteristic parameters of the foundation are discussed. The modified model further enriches and develops the elastic foundations. Relevant conclusions that are meaningful to engineering practice are drawn.

Structures such as beams, plates and shells are widely used,with various shapes, materials and models. Many engineering problems can be simplified as beams, plates and shells on elastic foundations, such as highway pavements, steel bearing plates on concrete, ships and bridges, and so on. Therefore, it is necessary to carry out a thorough and comprehensive analysis of the theory of structures on elastic foundations. Although many finite element software productions can solve this kind of problems, analytical solutions have great advantages in terms of understanding the essential aspects of physics and mechanics.

Considerable research has been dedicated to the study of the interaction between structures and complex media, and various theoretical systems for structures on elastic foundations have been developed. Vallabhan et al. [1-3] developed a refined model for beams and rectangular plates on elastic foundations. Dynamic analysis of thick plates including deep beams on elastic foundations was presented using modified Vlasov model [4]. A new two-parameter layer model which consisted of a number of elastic layers was presented and was solved through compiling layer stiff matrixes to form total matrix based on the principle of finite element method (FEM) [5]. A variational approach was used to examine the behavior of plates on elastic foundations including the effects of horizontal friction at the interface [6]. By using Laplace transformation and the reciprocal theorem of work, the solution of a new mechanical model was achieved,which showed the four joints of the edges of the plates as elastic boundary embeddings on the two-parameter viscoelasticity foundation under impact load [7]. In engineering practice, the soil medium is often regarded as Gibson soil, that is, the elasticity modulus of soil changes linearly with the depth [8]. A method for solving the problems of vibrations and bucking of a beam on a variable Winkler elastic foundation and a method for solving the problems of static analysis, vibrations and stability of beams on variable two-parameter elastic foundations were presented and compared [9,10]. A modified Vlasov soil model for Gibson soil was developed, and by using variational principle,the governing equation of beams on elastic layered Gibson foundations was derived [11,12]. In a word, the advantages of Vlasov two-parameter model have been proved in previous research.

However, these previous studies have some limitations. Most of the work on this subject is for the problem of a rectangular thin plate resting on a traditional Vlasov foundation. For example, the classical two-parameter foundation model is based on the assumption that the elastic layer is a homogeneous and isotropic elastic body. In fact, the elasticity modulus of the soil varies linearly with the depth of the foundation, that is, the assumption of a Gibson foundation is more consistent with the actual situation. On the other hand, the two-parameter foundation model combines the advantages of the Winkler foundation model and the elastic half-space foundation model and two independent elastic constants are used to represent the characteristics of the foundation soil. Nonetheless, the determination of the attenuation parameters γ is a difficult problem, which has hindered the further application of the Vlasov model. To overcome this problem, several methods have been suggested. A numerical iterative procedure in the light of FEM has been introduced to analyze plates resting on a two-parameter foundation[13]. An alternative variational formulation of Vlasov foundation model and an experimental investigation of Vlasov model have been presented [14,15].

Soil is a relatively complex and multi-phase discrete system.It is very difficult to determine the attenuation parameter for a Vlasov model. Researchers have mostly set attenuation parameters directly based on their engineering experience or specific experiments. In the present paper, the static bending of a circular thin plate on the modified Vlasov foundation has been analyzed based on the concept of Gibson soil. At the same time, the interaction between foundation soil and circular thin plates is systematically analyzed and the influence of soil inhomogeneity on the bending of circular thin plates resting on elastic foundations is discussed. Firstly, according to the principle of minimum potential energy, the governing equations and boundary conditions for a plate on the modified Vlasov foundation are established. Similarly, using the variational principle, the equations and boundary conditions for the attenuation parameter are also derived. Then, the attenuation parameter and two parameters are calculated using an iterative method. The deflections and internal force of circular plates are obtained relatively accurately.Finally, through parameter analysis, the effects of soil inhomogeneity on the bending of plates and the attenuation parameter and two parameters of modified Vlasov foundations are discussed. And some valuable conclusions for engineering practice are drawn.

In engineering practice, the modulus of elasticity Esof foundation soil varies with the depth H due to soil deposition. Considering the inhomogeneity of foundation soil, this paper assumes that the foundation is Gibson soil whose elasticity modulus varies linearly with the depth. Let the elasticity modulus of the top and bottom of a Gibson foundation be Es1and Es2, respectively.And the dimensionless parameter N is introduced

As shown in Figs. 1 and 2, the radius of the circular plate is a and the thickness is h. The radius of the lateral load q is b and the depth of the foundation is H . The elastic modulus Esat depth z is

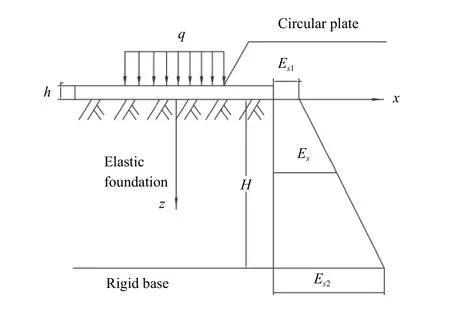
Fig. 1. Circular thin plate on an elastic Gibson foundation

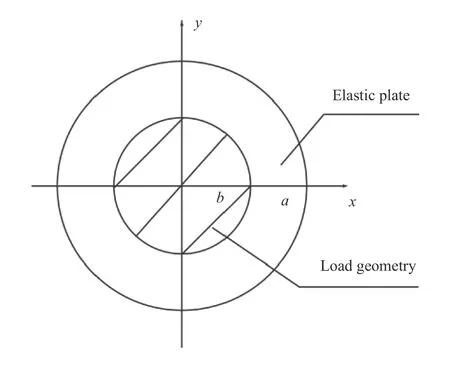
Fig. 2. Circular thin plate and load geometry

The total potential energy function for the plate and the soil continuum is given as where the physical quantities are the total potential energy function, the deformation potential energy of the circular plate,the deformation potential energy of the foundation, and the external force potential energy, respectively. The details are as follows

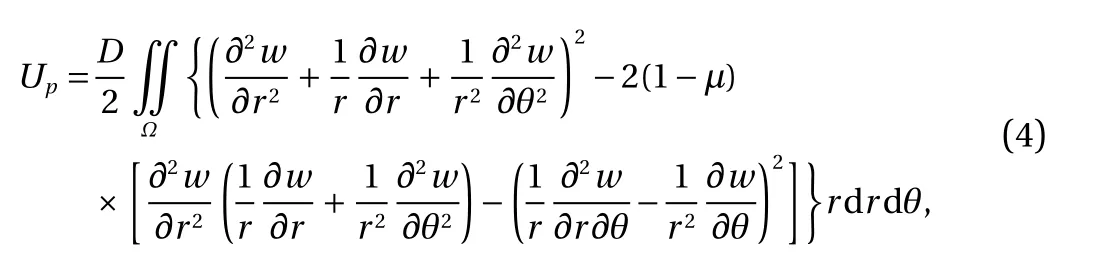
where D is the bending stiffness of the plate, E and μ represent the modulus of elasticity and the Poisson's ratio, respectively, w is the deflection of the circular thin plate, and Ω represents the region of the circular plate

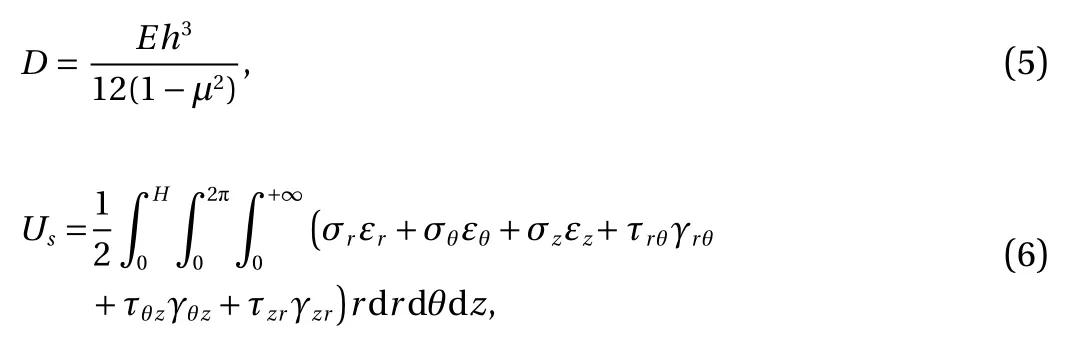
where σr,σθ,σz,τrθ,τθz,and τzrare the stress components of the foundation soil; correspondingly,εr,εθ,εz,γrθ,γθz,and γzrare the strain components of the foundation soil. The terms(ws,us,vs)represent the displacements of the foundation in the x,y and z directions, respectively. However, the horizontal displacements of the foundation are negligible compared with the vertical displacement in the z direction. For simplicity, it is assumed that us(r,θ,z)=0,vs(r,θ,z)=0 and the vertical deformation is ws(r,θ,z)=w(r,θ)φ(z), where φ(z) is a mode shape function defining the variation of ws(r,θ,z) in the z direction.

Substituting the constitutive relation and geometric relation into Eq. (6), the expression for potential energy of the foundation soil can be obtained as follows

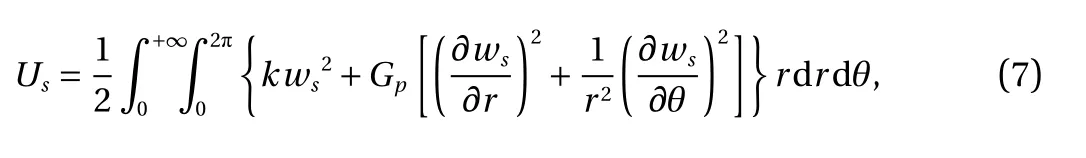
where wsrepresents the deflection of the foundation soil; the two parameters k and Gpare as follows

where μsis the Poisson's ratio of the foundation; and ΩSrepresents the surface area of the foundation, including the areaunder the circular plate and the areaoutside the circular plate. Mathematically all the two-parameter models are equivalent and differ only in terms of the definition of the foundation parameters.

External potential energy is

where Ωorepresents the area under lateral loads.

According to the the principle of minimum potential energy,the governing differential equations for the plate and that for the foundation soil surface outside the plate domain can be derived by complex variational deduction

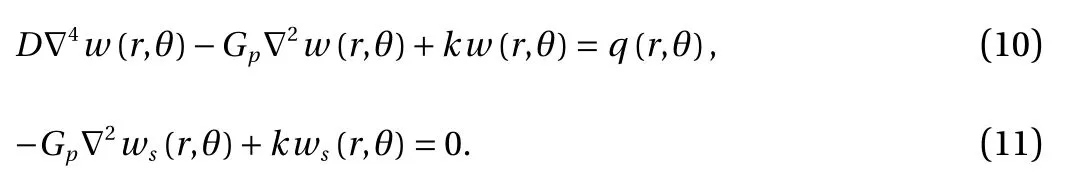
Similarly, collecting the coefficients of δ φ, the equation for the attenuation function φ is obtained as follows:

And the boundary conditions should be satisfied. The values of φ (0) and φ (H) are set equal to 1 and 0 respectively so that w(r,θ)represents the deflection of the foundation at the surface

where

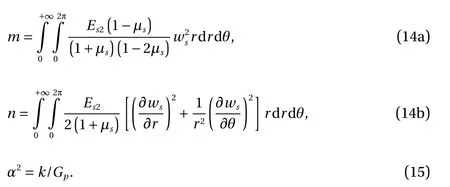
According to the differential equation and boundary conditions, the attenuation function and attenuation parameter are derived, which are the equations to be used in the iterative process

Determination of the γ parameter

Substituting Eq. (14) into Eq. (17), we get

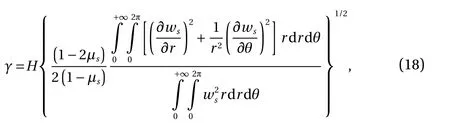
where γ herein is a dimensionless parameter, as opposed to the γused by Vlasov, which has a dimension of 1/length.

An effective iterative technique to solve the problem of a circular plate on a Gibson foundation using modified Vlasov model is shown below.

Step 1. Assuming an approximate value of the third parameter γ1, initially, the values of the two parameters k and Gpare evaluated using Eq. 8(a) and (b).

Step 2. By solving the governing Eqs. (10) and (11) and the corresponding boundary conditions, the deflection values of the circular thin plate and the foundation can be obtained.

Step 3. By using the solutions for the deflections of the circular thin plate and the foundation, a new value of γ2is computed using Eq. (18).

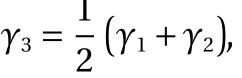
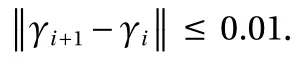
To illustrate the problem, only the case where the various parameters are axisymmetric is considered. That is, a circular thin plate resting on a modified Vlasov foundation is subjected to uniform circular loads and the range of load radius isThe loaded region 0 ≤r ≤b and unloaded region b ≤r ≤a of the circular thin plate and unloaded region r ≥a of the foundation soil are considered, respectively. w1(r) and w2(r)represent the deflections of the circular plate in the loaded and unloaded areas, respectively; and w3(r) is the surface deflections of soil medium outside the circular plate [16,17].

According to methods of mathematical physics, the total solution of the differential equation is the sum of the special solution and the homogeneous solution. Then, to make the deflection of the circular plate real, the full solutions are expressed as real functions as follows

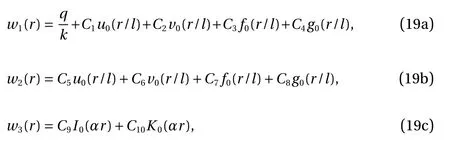
where C1,C2,···,C10are arbitrary constants; I0and K0are modified zero-order Bessel functions of the first and second types, respectively; l4=D/k; u0(r/l) and f0(r/l) represent the real parts of the zero-order Bessel and Hankel functions, and v0(r/l)and g0(r/l) represent the imaginary parts. The value of the constants can be determined by using the boundary conditions for the circular thin plate and the continuous conditions between the plate and foundation soil. Then, the complete solutions for the deflection and internal force of circular thin plates resting on elastic Gibson foundations can be obtained.The rotation angle, bending moment, and shear force of the circular plate can also be obtained.

For the free boundary r =a of the axisymmetric problem, the boundary conditions are as follows

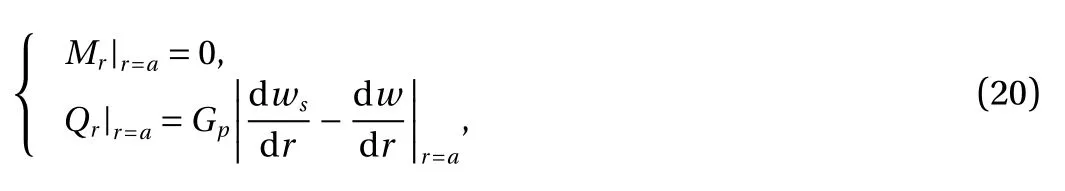
where Mrand Qrare the bending moment and shear force,respectively. The governing equations and boundary conditions are consistent with those of thin plates on traditional twoparameter foundations after degradation. However, the expressions for two parameters in the modified Vlasov foundation model are changed, which are related to the elasticity modulus of the soil.

The radius of the applied load is classified into two extreme cases and one general case.

Firstly, the radius of the uniform circular load is b =a. We consider a circular thin plate resting on an elastic Gibson foundation which is subjected to uniform external loads over its entire area with a stress q. With the assumption that rotation angle and shear force are zero at the center of the circular thin plate, it can be concluded that C3=C4=0. To satisfy the condition that the surface deflection at infinity is zero, then C9=0 is obtained. The remaining arbitrary constants can be determined from the following boundary conditions

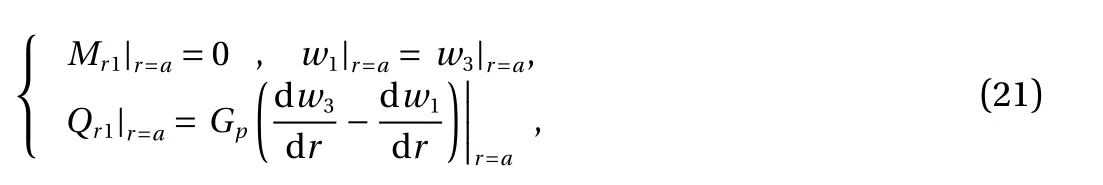
where Mr1and Qr1are expressions for bending moment and shear force obtained from w1(r).

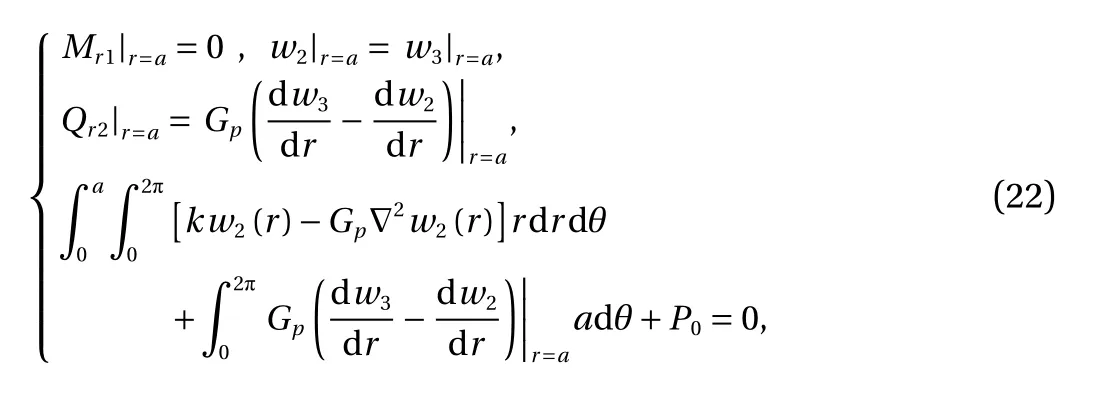
where Mr2and Qr2are expressions for bending moment and shear force obtained from w2(r), respectively. When the circular thin plate is subjected a concentrated force P0at the center, the method for solving uniformly loaded circular plates is still applicable, assuming that the central concentrated force is distributed over a circular area with a very small radius.

Finally, the radius of the uniform circular load is b ∈(0,a).Some equations can be derived by using the boundary conditions and displacement continuous conditions of circular plates on elastic foundations, and the number of these equations is equal to the number of undetermined coefficients.

The primary goal of this paper is to use the modified Vlasov model to simulate a Gibson elastic foundation and use the iterative method to solve the attenuation parameter γ for the modified Vlasov foundation model.

Example 1: The case of a circular thin plate subjected to uniformly distributed loads over its entire area is studied. The parameters of the circular plate on the Gibson elastic foundation that are to be calculated are: the radius of the circular plate r =0.4 m,thickness of the plate h =0.05 m, elasticity modulus of the plate E = 2.8 ×1010N/m2, the Poisson's ratio of the plate μ =0.15,elasticity modulus at the bottom of the Gibson soil Es2= 6.9 × 107N/m2, the Poisson's ratio of the foundation μs=0.3, depth of the foundation soil H =1.0 m and the uniform distributed load applied to the whole circular plate, q = 1 × 106N/m2.

When the characteristic parameters of the Gibson foundation are chosen as N =1/3,N=1,N=3, respectively, the calculation results of various parameters and the deflections of the circular plate are shown in Table 1. The w in the table refers to the deflection of the center of the circular plate. The deflections of the circular plate and Gibson foundation when N =1 are shown in Fig. 3. And Fig. 4 presents the bending moment diagram for the plate. The trends of the diagrams are in line with the reality.

It can be seen from Table 1 that the deflection of the circular plate at the center is 5.083 mm, which is compared with that from Ref. [18]. This proves the correctness of the calculation and programs in this paper. It can be seen from the Fig. 3 that the foundation soil outside the range of the circular thin plate is also deformed, but the deformation attenuation rate is very fast.

Example 2: The case of a circular thin plate subjected to local uniform lateral loads at the center is studied. The parameters of the circular plate on the Gibson elastic foundation that are to be calculated are: radius of the circular plate a =1.35 m, thickness of the plate h=0.25 m, elasticity modulus of the plate E=2.45×1010N/m2, the Poisson's ratio of the plate μ=1/6,elasticity modulus at the bottom of the Gibson soil Es2=6.25×107N/m2, the Poisson's ratio of the foundation μs=0.25, depth of the foundation soil H =2 m and local uniform distributed load with radius b =0.18 m applied at the center of circular thin plate. q =1×106N/m2.

When the characteristic parameters of the Gibson foundation are chosen as N =1/3,N=1,N=3, respectively, the calculation results of various parameters and the deflections of the cir-cular thin plate are shown in Table 2. The deflections of the circular plate and Gibson foundation when N =1 are shown in Fig.5.

23 Who knows what may not happen before that? thought the miller s daughter; and besides, she saw no other way out of it,24 so she promised the manikin what he demanded,25 and he set to work once more and spun the straw into gold

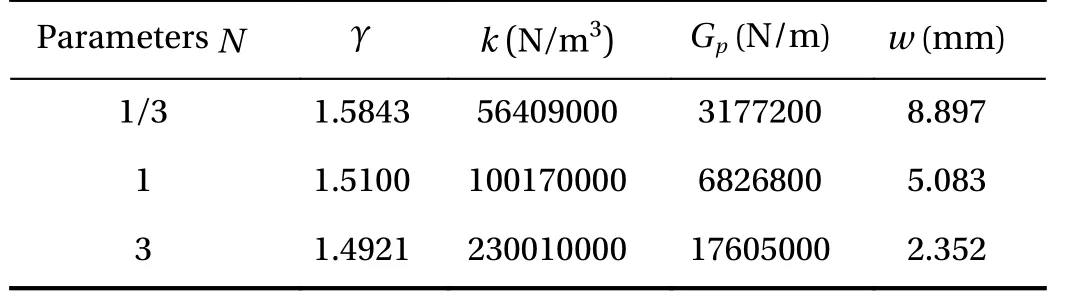
Table 1 Model parameters obtained from the three different foundations in Example 1.

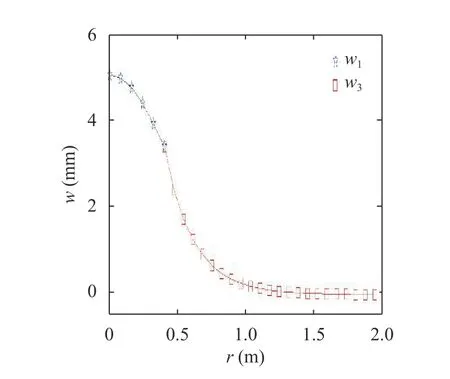
Fig. 3. Deflection of the circular plate and foundation soil

It can be seen from Table 2 that the deflection of the circular plate at the center is 0.345 mm, which is close to that obtained by previous studies [19]. The reason for the error is that the model used in the literature is a circular plate on a Winkler foundation,and the relevant parameters are not exactly the same. It can be seen from the Fig. 5 that the soil outside the range of the circular thin plate is also deformed. However, when it is 3 m away from the center of circular thin plates, the deformation of the foundation approaches zero.

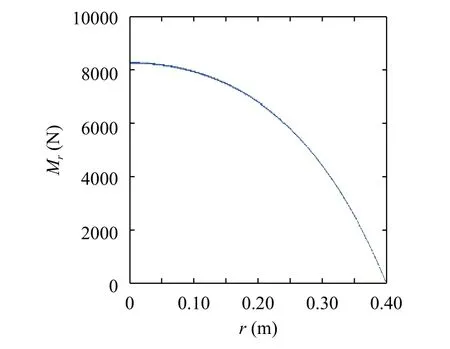
Fig. 4. Bending moment of the circular plate in Example 1

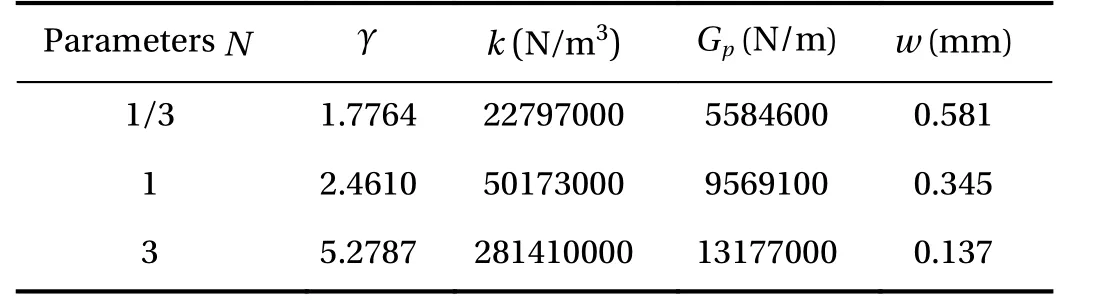
Table 2 Model parameters obtained from the three different foundations in Example 2.

Fig. 5. Deflection of the plate and foundation in Example 2

Example 3: The case of a circular thin plate subjected to a concentrated lateral load at the center is studied. The parameters of the circular thin plate on the Gibson elastic foundation that are to be calculated are: radius of the circular plate a =5 m,thickness of the plate h =0.5 m, elasticity modulus of the plate E=1.7658×1010N/m2, the Poisson's ratio of the plate μ =0.17,elastic modulus at the bottom of the Gibson soil Es2=8.6×106N/m2, the Poisson's ratio of the foundation μs=0.2,depth of the foundation H=1 m and the concentrated load P=9.81×104N . The radius of the load is b=0.01 m, small enough to simulate the concentrated load, and facilitates the calculation.

When the characteristic parameters of the Gibson foundation are chosen as N =1/3,N=1,N=3, respectively, the calculation results of various parameters and the deflections of the circular plate are shown in Table 3. The deflections of the plate and Gibson foundation when N =1 are shown in Fig. 6.

It can be seen from Table 3 that the deflection of the circular plate at the center is 0.320 mm, which is consistent with the calculation results of various methods in Ref. [20]. It proves the reliability of the analysis and calculation methods used in this paper. It can be seen from the Fig. 6 that the deformation w3of the foundation soil outside the range of the circular thin plate is very small.

(1) The effects of the inhomogeneity of foundation soil on the two parameters and the attenuation parameter are studied. All conditions, except the physical parameters of the Gibson foundation, are kept the same, and three kinds of foundation soil with different characteristics are selected for comparative analysis.The details and the numerical results are shown in Examples 1,2, and 3.

It can be seen from Tables 1, 2, and 3 that the inhomogeneity of foundation soil has a certain impact on various parameters.Further research also shows that the harder the surface foundation soil is, the greater the vertical elastic coefficient k is. The vertical elastic coefficient k of a Gibson foundation is mainly determined by the stiffness of the soil in the surface layer of foundations, which should be taken into account in engineering practice.

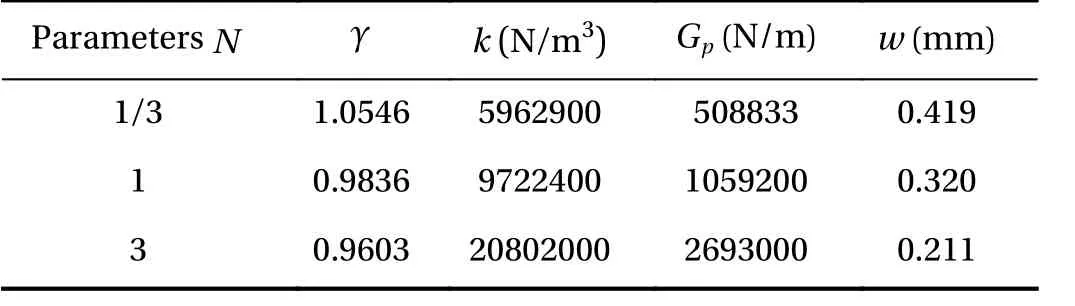
Table 3 Model parameters obtained from the three different foundations in Example 3.

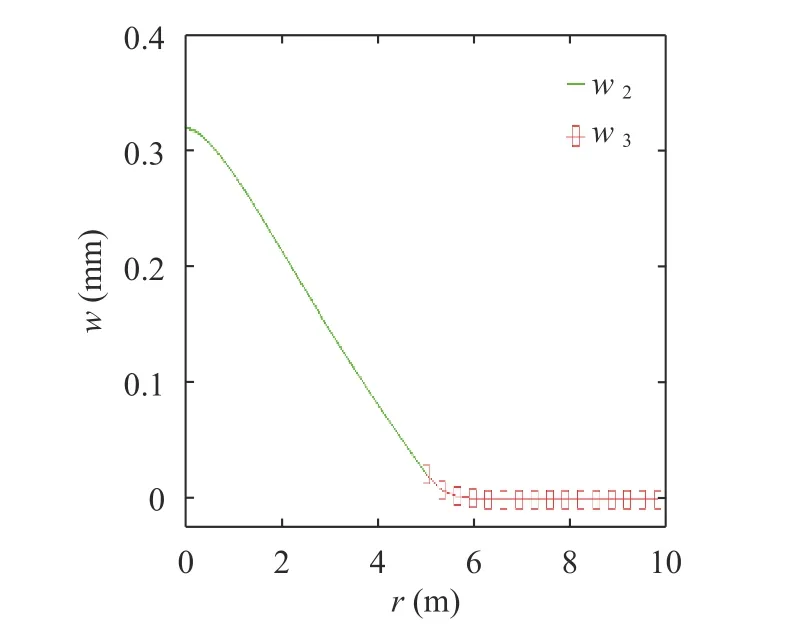
Fig. 6. Deflection of the plate and foundation in Example 3

(2) The effects of the inhomogeneity of soil on the bending of circular plates on elastic Gibson foundation are studied. It can be seen from Tables 1, 2, and 3 that the inhomogeneity of the soil has a great influence on the bending displacements of circular plates on the Gibson elastic foundations around the loads.However, little effect on the deflection of foundations is seen far away from the loads. In the two extreme cases and the the general case, the deflections of plates on Gibson elastic foundations decrease with the increase in N . Further research also shows that the bending deflections of a circular thin plate on Gibson elastic foundations are mainly affected by the stiffness of the surface of the foundation soil, and are less affected by the deep part of the soil. Therefore, in order to reduce the deflections of foundations in engineering, it is effective to improve the physical properties of the foundation soil at a certain depth, such as increasing its strength. Nonetheless, the effect of strengthening the deep foundations will be limited.

(3) The effects of load geometry on the two parameters and the attenuation parameter are studied. Under the same other conditions, only the radius of uniform loads at the center changes, which is 1/8-7/8 of the radius of circular plates respectively. Figure 7 shows the trends of the attenuation parameters γ,and Fig. 8 shows the trends of the vertical elastic coefficient k.

It can be seen from Figs. 7 and 8 that load geometry has certain influence on the parameter k and the attenuation parameter γ. When the radius of uniform loads increases gradually, the parameter γ and coefficient k decrease gradually until they stabilize. Further research also shows that the two parameters and the attenuation parameter are different when the radius of the loads are different, including concentrated loads and uniform loads.

(4) The effects of other parameters of the system on the two parameters, the attenuation parameter, and the bending of circular plate are studied. Under the same other conditions, only a certain parameter changes, such as the depth of foundations,elasticity modulus of plates and the value of loads. For example,it can be seen from Figs. 9 and 10 that as the depth of the soil layer increases, the attenuation parameter γ also increases, and the vertical elastic coefficient k decreases.

Further research also shows that when the elasticity modulus of the circular plates increases, the deflections of the circular plates on elasticity foundation decrease. However, the attenuation parameter and the two parameters remain almost the same. When the uniformly distributed loads increase, the deflections of the circular plates on an elastic foundation increase in multiply; however, the attenuation parameter and two parameters remain almost the same.

Fig. 7. Attenuation parameter for different load geometries

The attenuation parameter represents the change of the deflection of foundation soil along the z-axis. The iterative process is repetitive and the conditions for the end of the cycle must be set. The number of runs, the time required, and the accuracy of the results are affected by computer performance, the initial values of the parameters, and the programming language, and so on. In addition, convergence is faster if the first estimation of γ is close to the exact value. In Table 4, M represents the number of iterations of the program. Then γ1, γ2, and γ3are the attenuation parameters of circular thin plates resting on modified Vlasov foundations subjected to lateral loads as shown in Example 1, respectively, corresponding to N =1/3,N=1,N=3.

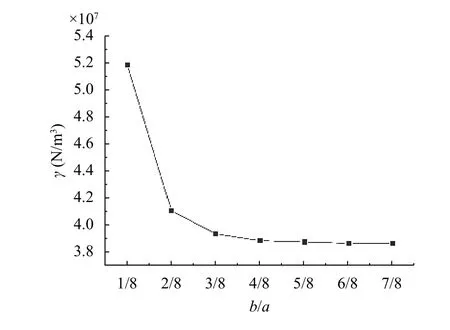
Fig. 8. for different load geometries

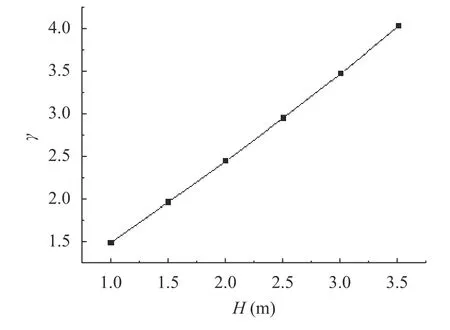
Fig. 9. Attenuation parameter for different foundation depths

Based on the modified Vlasov elastic foundation model, we have analyzed and calculated the bending problem of circular thin plates on elastic foundations, considering that the foundation is Gibson soil with finite depth. At the same time, the effects of the inhomogeneity of the foundation soil on the bending of thin plates and the characteristic parameters of the foundation model are also studied in this paper. Through theoretical derivation and numerical calculation, the conclusions are as follows.

(1) The work begins with total deformation potential energy of the foundation-plate system. Based on the principle of minimum potential energy, the governing differential equations and boundary conditions for the circular thin plate on elastic foundations can be derived through reasonably assuming the law of deflection attenuation and performing mathematical variational operations. There is no difference in form between the equations and boundary conditions for circular plates on modified Gibson foundation and those for circular plates on traditional Vlasov foundation; however, the related parameters are different.

(2) The traditional Vlasov foundation model assumes that the elastic layer is homogeneous and isotropic; however, the elasticity modulus of the foundation soil is non-uniform with the depth due to sedimentation. For the foundation soil, the assumption of Gibson soil is more in line with engineering practice than the traditional assumption considering foundation soil as homogeneous. The results show that the inhomogeneity of soil has a certain impact on the deflection and internal force of circular plates and on various characteristic parameters of the modified Vlasov model, which should be taken into account in practice. The mechanical behaviors of the plate and foundations are mainly determined by the characteristics of the shallow foundation soil under structures, not the deep part of foundations. In engineering practice, it can be considered to enhance the performance of the shallow part of the foundation, in order to improve the performance of the structure and foundation.

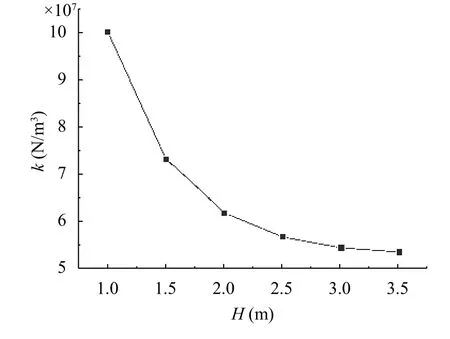
Fig. 10. for different foundation depths

Table 4 Attenuation parameters of the three different elastic Gibson foundations

(3) Considering the characteristics of Gibson soil, the modified Vlasov model still uses two independent parameters to represent the compressive and shear properties. For the key attenuation parameter γ, better results can be obtained by using the iterative method. The attenuation parameters are related to the depth of foundations, the elasticity modulus distribution of the foundation soil and the load geometry, but not related to the values of lateral loads, the elasticity modulus and thickness of circular thin plates. This shows that attenuation parameters determined by engineering experience or specific experiments are not accurate and reliable. This paper has enriched and extended the content of the elastic foundation model and promoted its wider application.

Acknowledgments

The study described in this paper was financially supported by the National Natural Science Foundation of China (Grant 51278420) and the Natural Science Foundation of Shaanxi Province (Grant 2017JM5021).