Thermoelastic waves in helical strands with Maxwell-Cattaneo heat conduction

Dnsong Zhng, Mrtin Ostoj-Strzewski

a Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA

b Department of Mechanical Science and Engineering, Institute for Condensed Matter Theory and Beckman Institute, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA

Keywords:Helical strands Maxwell-Cattaneo heat conduction Thermal relaxation Dispersion relation

A B S T R A C T Harmonic thermoelastic waves in helical strands with Maxwell-Cattaneo heat conduction are investigated analytically and numerically. The corresponding dispersion relation is a sixth-order algebraic equation, governed by six non-dimensional parameters: two thermoelastic coupling constants, one chirality parameter, the ratio between extensional and torsional moduli, the Fourier number, and the dimensionless thermal relaxation. The behavior of the solutions is discussed from two perspectives with an asymptotic-numerical approach: (1) the effect of thermal relaxation on the elastic wave celerities, and (2) the effect of thermoelastic coupling on the thermal wave celerities. With small wavenumbers, the adiabatic solution for Fourier helical strands is recovered.However, with large wavenumbers, the solutions behave differently depending on the thermal relaxation and chirality. Due to thermoelastic coupling, the thermal wave celerity deviates from the classical result of the speed of second sound.

Helical strands, or helically wound cables, are made of layers of individual helical wires wrapped around a common central axis. They are seen in ropes and power transmission cables. Similar structures are also present in biological tissues in the form of helical-fiber-reinforced composites. Regardless of the distinct applications, the helical wrapping in such structures introduces mirror asymmetry, i.e. chirality, resulting in effective properties not present in the base material. We have previously developed a thermomechanical Timoshenko rod model for helical strands and solved the dispersion relation of thermoelastic waves with Fourier's heat conduction law [1]. The model incorporates the coupling between thermal expansion and torsion.

Motivated by the well-known limitations of the Fourier law[2], the present study focuses on thermoelastic waves in helical strands with the Maxwell-Cattaneo heat conduction law. This law also has the advantage of being more accurate for phenomena with very short time intervals [3] or very high heat fluxes [4],as well as materials with significant thermal relaxation [5]. According to Ref. [1], the elastic waves transition from an adiabatic regime to an isothermal regime as the wavenumber increases,the transition regime being determined by the Fourier number.As demonstrated in Ref. [6], there is a critical wavenumber below which the temporally attenuated harmonic wave solution for a one-dimensional (1D) Maxwell-Cattaneo heat equation is diffusive and above which the solution is wave-like; and as the wavenumber approaches infinity, the heat wave celerity approaches the speed of second sound.

In this paper, the thermo-elastodynamics of helical strands is discussed from two angles: (1) the effect on the elastic waves of the heat conduction changing from Fourier-type to Maxwell-Cattaneo-type; (2) the change of the thermal wave as the 1D Maxwell-Catteneo heat equation becomes coupled with the elastic field in helical strands due to thermoelasticity and chirality.

We consider a helix wound at a constant lay angle β around the axis x3. Figure 1 shows six such helices (or helical strands)with the analysis in this paper applicable to a single strand or a bundle of parallel strands [7]. The helix is unstressed in this reference configuration and at rest. The objective is to describe the thermoelastic response of a helix with reference to x3, as if it were a straight rod.

Fig. 1. Helically wound cable showing a bundle of six helical strands with lay angle wound around a central straight core that is aligned with

Just as in Refs. [1, 7], the elastic response is linear, so that with all the displacements and strain assumed small, the overall elastic response is also linear. The thermal conductivity response is assumed to follow the Maxwell-Cattaneo law

where Q is the heat flux in the helix' cross section, τ is the thermal relaxation time, A =πR2is the cross-sectional area of the projection of the helix on a plane orthogonal to x3, K is the thermal conductivity, and Θ is the absolute temperature. Also,an overdot denotes the time derivative ∂/∂t, and a prime denotes the spatial derivative ∂ /∂x3.

The thermo-elastodynamic equations of a linear elastic helix,albeit with the heat conduction governed by the Fourier law,have been derived and presented in Ref. [1]. Proceeding in an analogous way and focusing on axial, torsional, and thermal responses respectively, it is straightforward to find this set of three governing equations for Maxwell-Cattaneo heat conduction

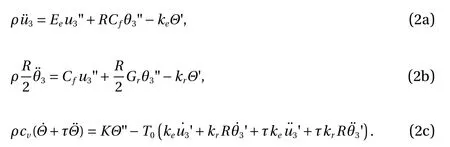
Here u3is the axial displacement and θ3is the angle of twist. The material and geometric parameters are: the helix' radius R, mass density ρ, reference temperature T0, elastic extensional modulus Ee, elastic torsional modulus Gr, tension-torsion coupling Cf,tension-temperature coupling ke, torsion-temperature coupling kr, and specific heat cv.

Overall, the model Eq. (2) is entirely hyperbolic, whereas the model of Ref. [1] was parabolic in heat conduction (due toτ=0 in Ref. [1]) and hyperbolic in elastic response. Strictly speaking,the investigation reported in Ref. [1], and based on Ref. [8] dealt with the three-dimensional (3D) mechanics of a helically wound cable, effectively modeled as a Timoshenko rod with all six degrees of freedom in any cross-section: the axial displacement(u3) , two transverse displacements (u1and u2), the angle of twist( θ3) and two bending angles ( θ1and θ2). That study examined all the thermo-mechanical interactions and possible wave motions,thereby establishing that the torsional response is coupled to the thermal expansion due to the chirality of the helix, an aspect which, of course, carries over to the case of a helix with hyperbolic-type heat conduction. The challenge ahead of us is to examine the wave propagations - axial, torsional, and thermal - admitted by the model Eqs. (2a) and (2c).

Assuming harmonic solutions in the form exp[ ik (x-ct)],k ∈R+, we readily arrive at the dispersion relation

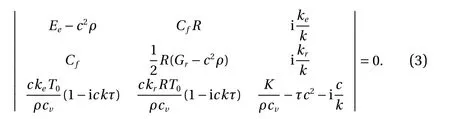
This is a sixth-order algebraic equation in c, and thus no explicit forms of solutions exist in general. We therefore take a combined asymptotic-numerical approach to determine the properties of solutions. To make the discussion more general,the equation is first fully non-dimensionalized to

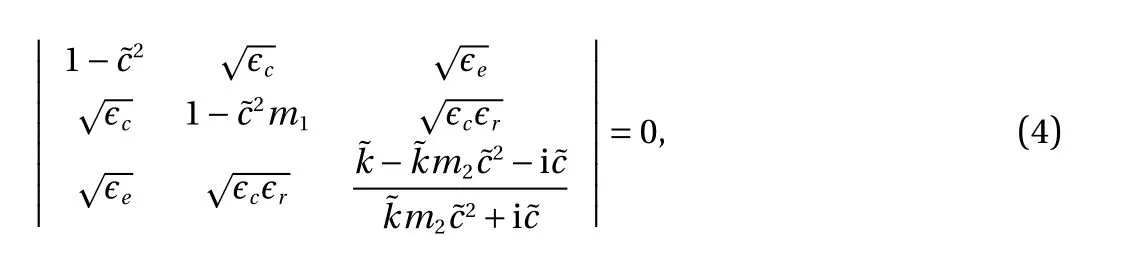
where the chirality and thermoelastic coupling parameters for the longitudinal and torsional modes are, respectively

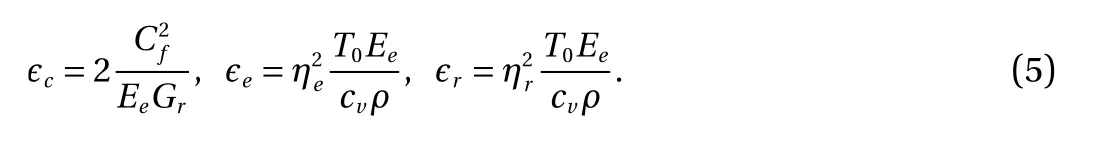
The wavenumber k and the celerity c are also non-dimensionalized

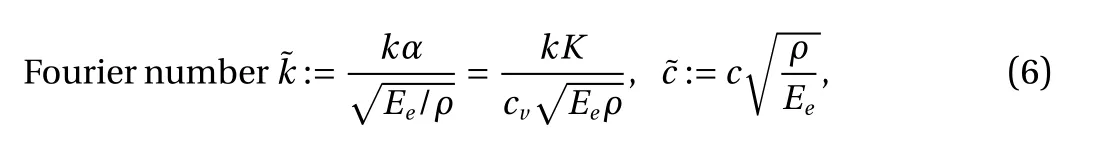
with α =K/(ρcv) being the thermal diffusivity [8]. The Fourier numbercharacterizes the rate of thermal diffusion relative to the rate of propagation of axial elastic perturbation. We also have

In a fully uncoupled system, the longitudinal, torsional, and heat wave celerities are, respectively,

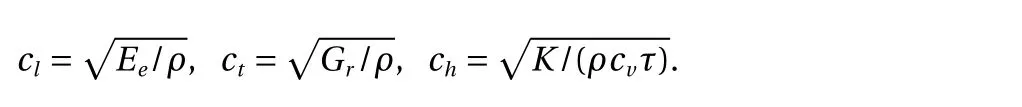
Thus, it is straightforward to see the physical meanings:m1=(cl/ct)2, and m2=(cl/ch)2. Typically, the extensional modulus is greater than the torsional modulus, i.e., m1＞1. The value of m2can vary significantly depending on the thermal relaxation time τ of the material. Values on the order of picoseconds or less for homogeneous liquids and solids have been reported [9-11],whereas in materials with non-homogeneous inner structures,τ can be tens of seconds [12, 13]. Of course, as τ (i.e., m2) approaches 0, the heat conduction reduces to a Fourier type.

In terms of the introduced non-dimensionalization, in a fully uncoupled system, the longitudinal, torsional, and heat wave celerities areandrespectively. We assume m1＞1 in the following analysis.

As k approaches 0, the adiabatic solution for Fourier heat conduction derived in Ref. [1] is recovered, independent of the non-dimensional thermal relaxation m2

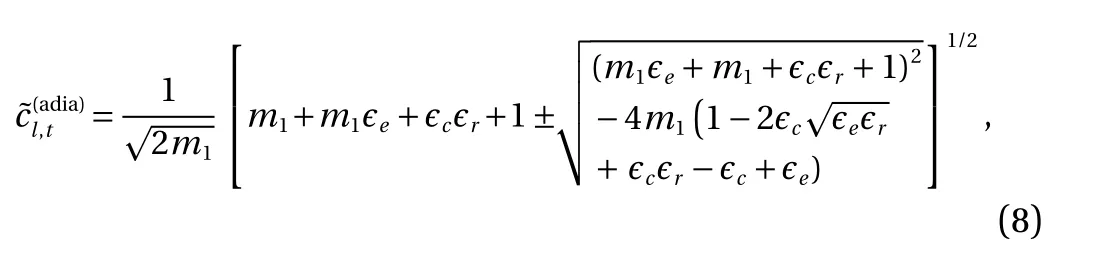
where "+" ("-") stands for the quasi-longitudinal (quasitorsional) wave. Here "quasi" means that the longitudinal mode is always coupled with a small torsional motion and vice versa,due to chirality. Similarly, the thermal wave is also "quasithermal", as a temperature perturbation is always coupled with elastic waves. For brevity, we omit "quasi" in the following writing.

However, with large wavenumbers, the solution is affected by the thermal relaxation. With Fourier heat conduction, the elastic waves approach the isothermal limit as the wavenumber approaches infinity, where the celerities are the same as in the case of no thermoelastic coupling

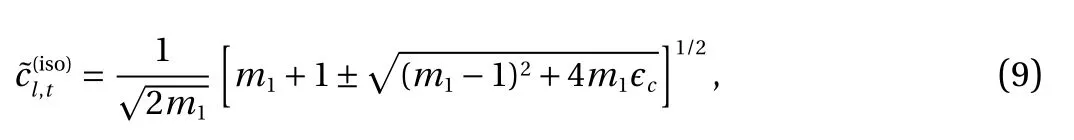
with "+" for the longitudinal wave, and "-" for torsional. With Maxwell-Cattaneo heat conduction, taking the limit, the dispersion relation becomes While this equation can be solved explicitly, the solutions are too involved to offer a clear insight into the physics. In general, the

solution depends on m2. Physically, the temperature perturbation travels at a finite speed, and thus the isothermal state is not necessarily achieved even for an infinite wavenumber. When m2is very small, the temperature perturbation travels very fast compared with the elastic waves,and therefore, the behavior of the solution resembles that of the Fourier heat conduction. However, when the temperature perturbation travels slower than the elastic waves, the solution can exhibit qualitatively different behavior. These two cases are discussed below in detail.

When m2≪1, heat propagates much faster than elastic waves. The presence of m2introduces small perturbation to solutions for Fourier heat conduction. The asymptotic expansion of solutions to Eq. (10) is obtained as

The expression for the first-order coefficient is too complicated to be displayed here, but it is linear in єe, єrandthus the notation O (єe,r). In other words, for a Maxwell-Cattaneo heat conduction with small thermal relaxation, the elastic wave celerities are perturbed by a small amount that is proportional to the non-dimensional thermal relaxation m2and the thermoelastic coupling parameters. To see the effect of chirality, an asymptotic expansion of the first-order coefficient in the limit of small lay angle and small thermoelastic coupling (assuming єe=єr) gives

Therefore, with small thermal relaxation, both the longitudinal and the torsional wave celerities are reduced from the isothermal solutions, with the amount of reduction proportional to the thermoelastic coupling and the thermal relaxation. In particular, the reduction of the torsional celerity is a result of chirality,i.e., for a non-chiral rod, the torsional celerity is the same as its isothermal counterpart. As a numerical example, the variation of the longitudinal and torsional celerities with the Fourier numberis shown in Fig. 2, with relatively small m2values. Indeed,the elastic wave celerities in the short-wave limit decrease with increasing thermal relaxation. When m2=0, the isothermal solution is recovered. The reduction of the torsional celerity is actually very small for this particular set of parameters. According to Ref. [1], the critical Fourier number for adiabatic-isothermal transition is

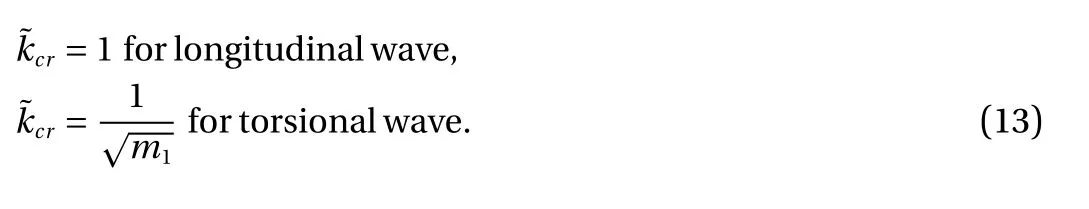
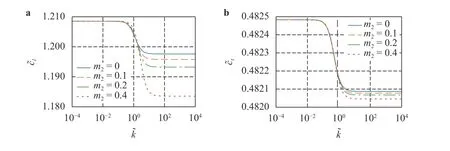
Fig. 2. Celerities of a longitudinal and b torsional waves as the wavenumber varies, with relatively small values of the thermal relaxation.Parameters: thermoelastic coupling , chirality, and modulus ratio. The vertical lines indicate the transition for Fourier heat conduction estimated by Eq. (13).

With Maxwell-Cattaneo heat conduction, there is no isothermal regime. However, Fig. 2 shows that a qualitative transition in the behavior of solutions also occurs at around the same values of

When m2≫1, heat propagation is much slower than elastic waves. Therefore, physically, it is close to the adiabatic case. This is proved with our asymptotic analysis. We have

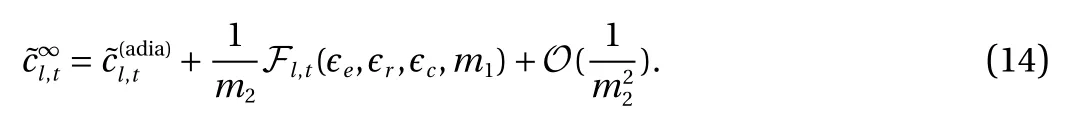
Here, the perturbation term Fl,tis a function of єe, єr, єcand m1. Again, an approximation of Fl,tin the limit of small lay angle and small thermoelastic coupling (assuming єe=єr) gives

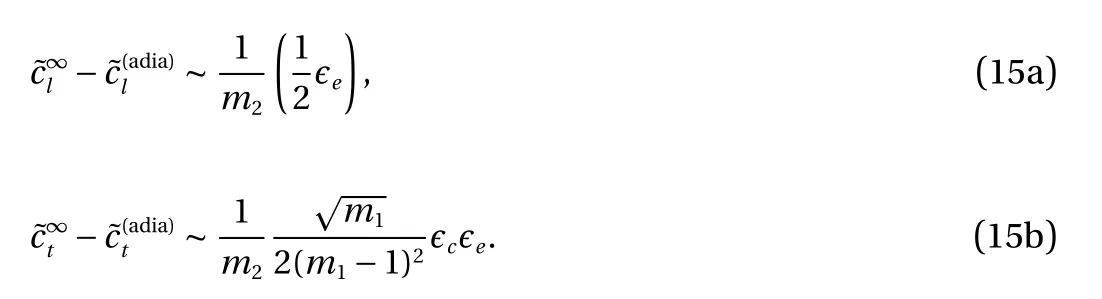
Therefore, with large thermal relaxation, the elastic wave celerities are greater than their adiabatic counterparts. In particular, the perturbation to the torsional celerity is a result of chirality.

The variation of the elastic wave celerities with the wavenumber for a particular set of parameters is shown in Fig. 3,with the thermal relaxation m2taking relatively large values. Indeed, the celerities at the limit of infinite wavenumber exceed the adiabatic solution, and the amount of excess decreases with increasing thermal relaxation. In a hypothetical situation where m2approaches infinity, the heat propagation rate approaches zero, and thus the solution reduces to the adiabatic solution.Note that we also have a transition as the Fourier number increases. This is related to the transition of the thermal solution from a pure diffusive type, to a wave type, in a similar way to the temporally attenuated and spatially periodic (TASP) solution for a 1D telegraph equation [6]. With Maxwell-Cattaneo heat conduction, the Fourier number needs to reach a critical value for wave-like thermal solutions to exist. Whenis below the critical value, the thermal roots are two pure imaginary numbers. Above the critical value, the thermal roots bifurcate into a pair of two complex numbers, with equal-and-opposite real parts and identical imaginary parts. For a single 1D telegraph equation, we found the bifurcation point to be

with α being the thermal diffusivity [6]. In a non-dimensional form

In helical strands, due to the thermoelastic coupling, the exact bifurcation point is different than this, but only very slightly.

An extensive discussion of harmonic wave solutions to a single telegraph equation in 1D has been given in Ref. [6]. In helical strands, the coupling of the thermal field with the elastic field changes the thermal wave solution.

In Eq. (4), if we assume no thermoelastic coupling, the isothermal elastic wave solutions, Eq. (9), are recovered. Indeed,the isothermal condition implies a decoupling of the thermal field from the elastic field. In the meantime, the thermal solutions are

It is quickly verified that this is the same as the TASP solution for a 1D telegraph equation [6]. In the limit of

which is the classical result for the speed of second sound in the Maxwell-Cattaneo heat conduction. With any finite wavenumber, the celerity is lower than this limit.

However, in helical strands, the thermal wave celerity is modified due to thermoelastic coupling. Assuming small thermoelastic coupling, we can do a perturbation analysis. For simplicity, we again assume єe=єr. The thermal solution is then essentially written as

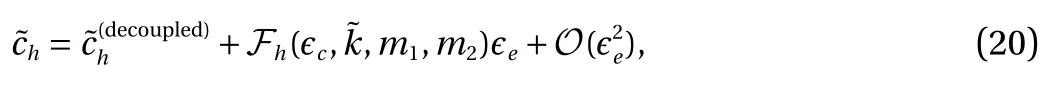
where Fhis a function of єc,m1and m2, and is in general complex (i.e., both the celerity and the damping are perturbed).In the limit ofi.e.,

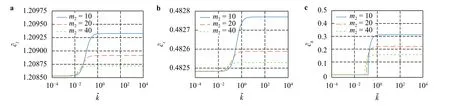
Fig. 3. Celerities of a longitudinal, b torsional and c thermal waves as the non-dimensional wavenumber varies, with relatively large values of the thermal relaxation. Parameters: thermoelastic coupling , chirality, and modulus ratio . Below the bifurcation point, the thermal solutions are two pure imaginary numbers, and hence the real parts (celerities) are zeros.

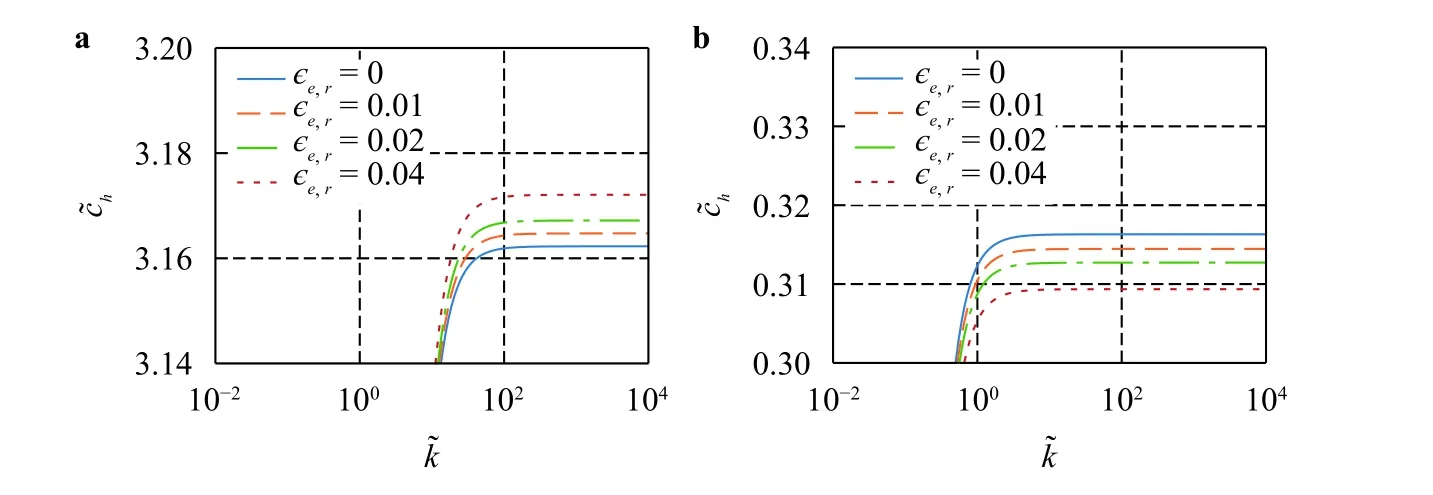
Fig. 4. Celerities of the thermal waves when a and b . represents the thermoelastic coupling parameters and, which are set equal here. Other parameters: modulus ratio and chirality.

Therefore, the speed of heat wave deviates from the classical speed of second sound due to thermoelastic coupling єe. To demonstrate the effect of chirality, we further obtain the approximation of Eq. (21) in the limit of small chirality

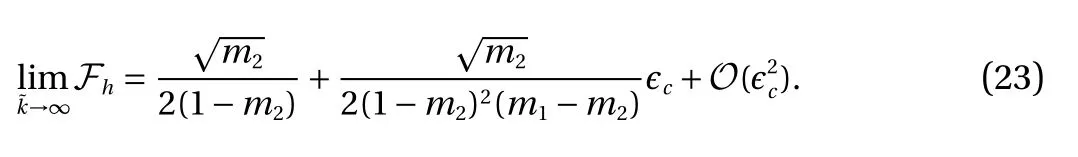
The leading term does not depend on chirality, i.e., for a nonchiral rod, the thermoelastic coupling still leads to a perturbation of the thermal wave celerity, as there is always a coupling between the elastic extensional mode and the thermal mode as a result of thermal expansion, regardless of chirality. Moreover,whether the heat wave celerity is increased or decreased from the speed of second sound depends on the thermal relaxation time m2. If m2＜1 (ignoring the higher-order terms in єcand єe),then the thermal wave celerity is increased, and in the meantime, the elastic wave celerities are decreased. The opposite is true if m2＞1. These asymptotic results are verified with numerical examples in Fig. 4.

In this paper, the dispersion relation for helical strands with Maxwell-Cattaneo heat conduction is derived from fully coupled longitudinal-torsional-thermal equations. Compared with Fourier heat conduction, the heat transport is controlled by not only diffusion, but also thermal relaxation. There is an additional non-dimensional parameter m2that characterizes the heat propagation rate compared with the longitudinal elastic propagation rate, whereas the nondimensional wavenumber (or Fourier number) characterizes the heat diffusion rate compared with the longitudinal elastic propagation rate. With small wavenumbers, the adiabatic solution for Fourier helical strands is recovered, regardless of the thermal relaxation time. However,with large wavenumbers, the solutions are different depending on the thermal relaxation. In the case of a small thermal relaxation, the heat transport is very fast, and the behavior of the elastic waves resembles that for Fourier heat conduction, with the wave celerities decreasing as the thermal relaxation increases. In the case of a relatively large thermal relaxation, the heat transport is slow, and the celerities of the elastic waves are slightly higher than the adiabatic solutions for Fourier helical strands. It is also found that, in both cases, the modification of the torsional wave celerities is a result of chirality. On the other hand, with thermoelastic coupling and chirality, the thermal wave celerity deviates from the classical result of the speed of second sound.While this paper investigated a 1D chiral thermoelastic problem,a reference is made to for 3D chiral continuum thermoelasticity[14, 15].

Acknowledgements

The authors acknowledge the helpful discussions with Dr.John P. D'Angelo. The work was supported by the National Science Foundation of United States (Grants IIP-1362146 and CMMI-1462749).