月面多机器人的分布式协同定位算法研究
2019-10-31魏明珠谢晓梅徐利梅
魏明珠,谢晓梅,严 鹏,徐利梅
(电子科技大学航空航天学院,成都611731)
1 引言
随着我国载人航天工程和月球探测工程的发展,月面探测的技术条件在不断突破,但月面环境苛刻,不适合人类的长期作业[1]。在有人参与的深空探测前期,需要无人深空探测任务突破关键问题[2]。目前机器人技术发展迅猛,很多领域理论渐趋成熟,应用研究也深入到工业、军事等多个层面。因此,利用月面机器人进行探测,可完成更广泛区域的月球科学探测任务,并为载人登月提供科学与工程数据和先期基础设施。携带各种传感器和采样装置的月面移动机器人是月面探测的重要工具[3-5]。单个机器人的负载能力、数据处理能力等有限,利用多个月面移动机器人系统可以获得更大的探测效率,通过分布式的信息处理获得更高效和更广泛的信息量[6]。
多机器人协同进行月表探测的前提是每个机器人能够快速准确地获得自身在环境中的位置信息,因此多机器人系统中的定位是首要问题[7-8]。多机器人系统作为一个整体,机器人之间的协同定位可以利用机器人彼此的信息,获得各自的位置。多机器人协同定位的方法有两类:一类是集中式协同定位,每个机器人的信息都传输到中央处理单元进行处理,然后再发送给各个机器人[9];另一类是分布式处理,即每个机器人利用与邻居机器人交互的信息计算自己的位置[10]。因此分布式定位方法具有实际的价值,也是人们研究的热点。Costa等[11]提出了基于分布式加权多维标度的算法,基于凸包中不含锚点的假设,利用质心计算方法,定位网络中机器人的位置,但成本函数本身建立比较复杂,算法的运算量较大。Cui等[12]采用不依赖锚点的分布式定位方法,本质是通过多边法的原理定位,定位后的节点作为虚拟锚点,该方法在网络拓扑结构上有局限。王玲等[13]提出了基于扩展卡尔曼滤波的相对位姿测量方法,该方法需要机器人交互除位置信息外还有方位信息,同时没有考虑大规模多机器人网络的定位情况。
本文重点考虑基于测距信息的多机器人系统的分布式定位问题,对多机器人协同定位问题建立优化方程模型,并提出基于自适应步长的分布式梯度下降的定位方法,通过仿真试验分析算法的性能。
2 多机器人系统问题建模
假设n个月面机器人构成一个自主移动的网络, p(τ)={pi(τ)},i=1,…,n, 表示 n 个机器人在τ时刻的位置,其中第i个机器人的位置表示为 pi(τ)=[xi(τ),yi(τ)]T。 D={dij},i,j∈ n,表示机器人之间的测距信息的集合。对于机器人i与j,dij表示机器人之间距离的测量值,而|pipj|表示两个机器人之间的真实距离,因此满足如下计算公式,表示两个机器人之间距离真值与测量值之间的误差。
假设机器人之间量测的距离信息组成集合ε,则系统目标是通过最小化均方差的拟合优度准则(式(1)),获得多机器人系统的最佳位置的估计,或者机器人通过移动形成最佳的预定的网络拓扑。
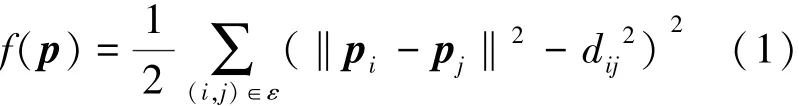
因此,多机器人系统定位问题表示为优化方程,如式(2)所示。
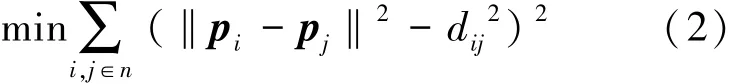
其中,pi和pj是待估计的机器人位置,dij是机器人之间的距离量测值。估计量与测量值之间的差越小,表明机器人估计的位置信息越准确。
3 基于梯度的分布式定位方法
3.1 梯度下降定位法
在优化理论中,采用梯度下降法可以获得目标函数的局部最优值。对于多机器人系统,如果将每个机器人看作一个节点,机器人之间的联系看作线段,则多机器人系统可以假设为一个图,若这个图是广义的全局刚性图,则上述优化问题具有唯一的最优值,即局部最优解就是该问题的全局最优解,因此每个机器人获得唯一的最优位置[14]。
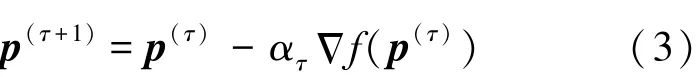
其中 ατ是步长;(p);Δgij(p) = 2[OT,…, (pi-pj)T,OT…OT,(pj-pi)T,…,OT],ij(p) 含有 n 个向量,每个向量的维数是2×1,因此ij(p)是一个包含2n个元素的行向量。
3.2 自适应步长的计算
在梯度下降法中,步长决定算法收敛的速度和稳定性,固定步长通常无法有效平衡收敛的快速性和稳定性,为此寻找合适的步长成为该方法的主要问题。这里采用了一种自适应的步长计算方法,Barzilai-Borwein步长(简称BB步长),可以在每次迭代过程中找到最大或最小的步长,从而提高算法效率。BB步长的计算公式为式(4)。
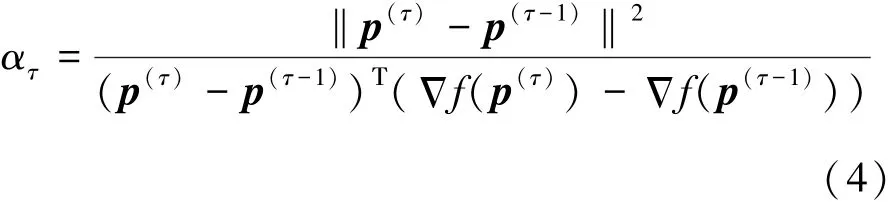
分布式梯度算法采用BB步长,分为2个阶段进行,第1阶段是分布式步长计算,第2阶段是每个机器人利用邻居的测量信息分布式迭代更新定位[15]。
3.3 BB步长的分布式计算
假设每个机器人都可以获得自身与近邻的当前位置信息和上一个时刻的位置估计。上述步长计算公式(4)中的分子和分母分别用标量θ和γ表示,则第 i个机器人在 τ(0)时刻的初值θi(τ(0)) 和γi(τ(0)) 如式(5)所示。

任意时刻τ(t+1)的θi(τ(t+1))和 γi(τ(t+1))迭代如式(6)、式(7)所示。
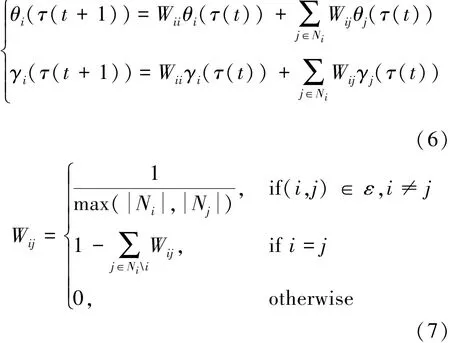
其中Wij满足Metropolis准则;Ni表示机器人i的邻居集合,即 Ni={j:(i,j) ∈ε}; Ni表述集合Ni的基数,即集合中元素个数。
对于多机器人系统构成的通信网络,如果该网络表示的图是连接图,即机器人之间可以彼此交互,则每个机器人在有限的时间内可以计算迭代步长,如式(8)所示。
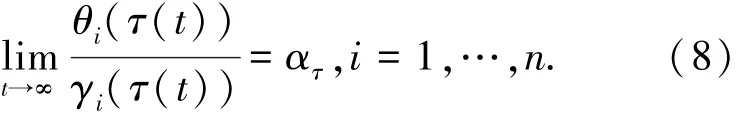
证明:式(8)中的分子写成如下形式:
θ(τ(t+1))=W·θ(τ(t)),θ(τ(t))=Wt·θ(τ(0)),其中,θ(τ)=[θ1(τ),…,θn(τ)]。 由于矩阵 W满足如下条件: Wkz-1ζ≤λ2(W)k·‖z‖, λ2(W)< 1,λ2(W) 是矩阵W的第2个特征值,ζ是向量z中所有元素的均值,则,‖θ(τ(0))‖。 由于 ‖·‖≥ ‖·‖∞( ‖·‖与‖·‖∞分别表示元素·的二范数与无穷范数),式(9)和式(10)成立。
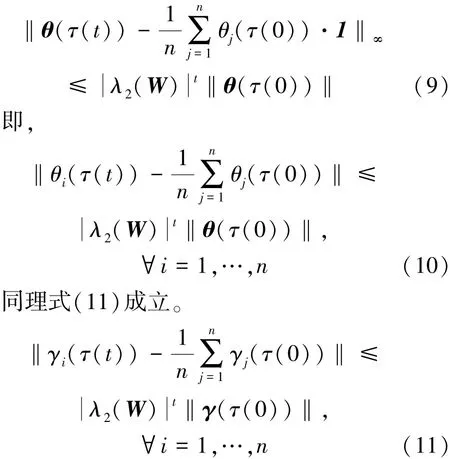
随着 t→∞,θi(τ(t))和γi(τ(t)) 分别收敛到 θ(τ(0))和 γ(τ(0)),因此各个机器人独立计算的迭代步长可以收敛到算法统一的步长值,如式(12)所示。
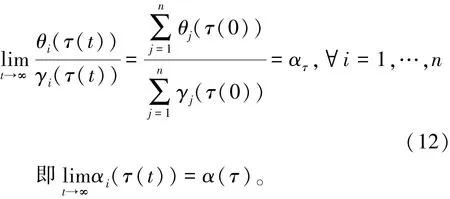
3.4 机器人位置更新过程
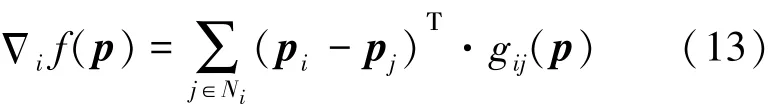
第i个机器人的位置更新过程如式(14)所示。
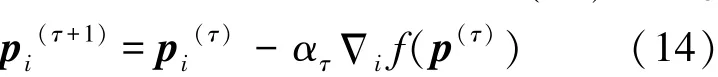
将式(13)代入到式(14),则每个机器人的位置更新的计算方法,如式(15)所示。

注意,式(15)表明每个机器人进行位置更新的时候,分布式步长αi(τ)已经收敛到一致的步长值ατ[16]。算法流程如下:
1)初始化。设定一致步长计算阶段最大的迭代次数tmax,定位容忍误差οtolerance。 假设位置更新迭代次数τ=0,对机器人位置进行初始估计,采用均匀分布或者高斯分布的位置假设。
2)一致步长的计算。假设t=0,根据式(5)计算 θi(τ(t)) 和 γi(τ(t));t=t+1,根据式(6)和式(7)更新θi(τ(t))和γi(τ(t)) ;直到t≤tmax停止迭代。
3)机器人位置更新。根据式(8)计算αi(τ(t));τ=τ+1,根据式(15)计算新的位置;当‖pi(τ+1)-pi(τ)‖≤οtolerance成立,停止位置更新。
4)输出每个机器人的定位终值。p(τ+1)=[p1(τ +1),…pn(τ +1)]。
4 仿真试验
多个机器人在未知环境中执行探测任务时,首先需要到达指定位置,即构成指定的多机器人网络。这里目标网络为平面上10个机器人构成的多机器人系统,如图1所示。图中节点表示机器人,虚线表示机器人之间的信息测量与交互关系;星号表示待定位的机器人位置;3个边界点表示锚点机器人,其位置已知,用于确定整个网络的全局坐标,由圆圈标识。根据图论可知对于二维的网络,如果至少3个非共线节点的绝对位置已知,那么整个网络有唯一拓扑结构,即多机器人网络中每个机器人位置有唯一的解。因此这里选用网络边界不共线的3个点作为锚点机器人。由于该算法是一种迭代方法,需要给每个机器人一个任意初始位置估计,如图2表示,用圆圈标识。为验证方法的收敛性,这里采用2种初值估计方法,第一假设初值在定位区域内符合均匀分布,如图2所示;第二假设初值在真实位置附近符合高斯分布。经过该算法的运算,任意一种分布的位置初值最终都会收敛到真实位置,即如图3中三角表示的位置。
假设机器人初始位置估计满足在给定区域[1 m×1 m]内的均匀分布,分布式步长迭代次数tmax=20,每个机器人独立采用分布式梯度方法,其位置估计误差的收敛过程如图4所示。每个机器人位置估计误差收敛到给定的容忍误差范围之内,即οtolerance=10-12,试验中位置更新迭代次数τ小于80。
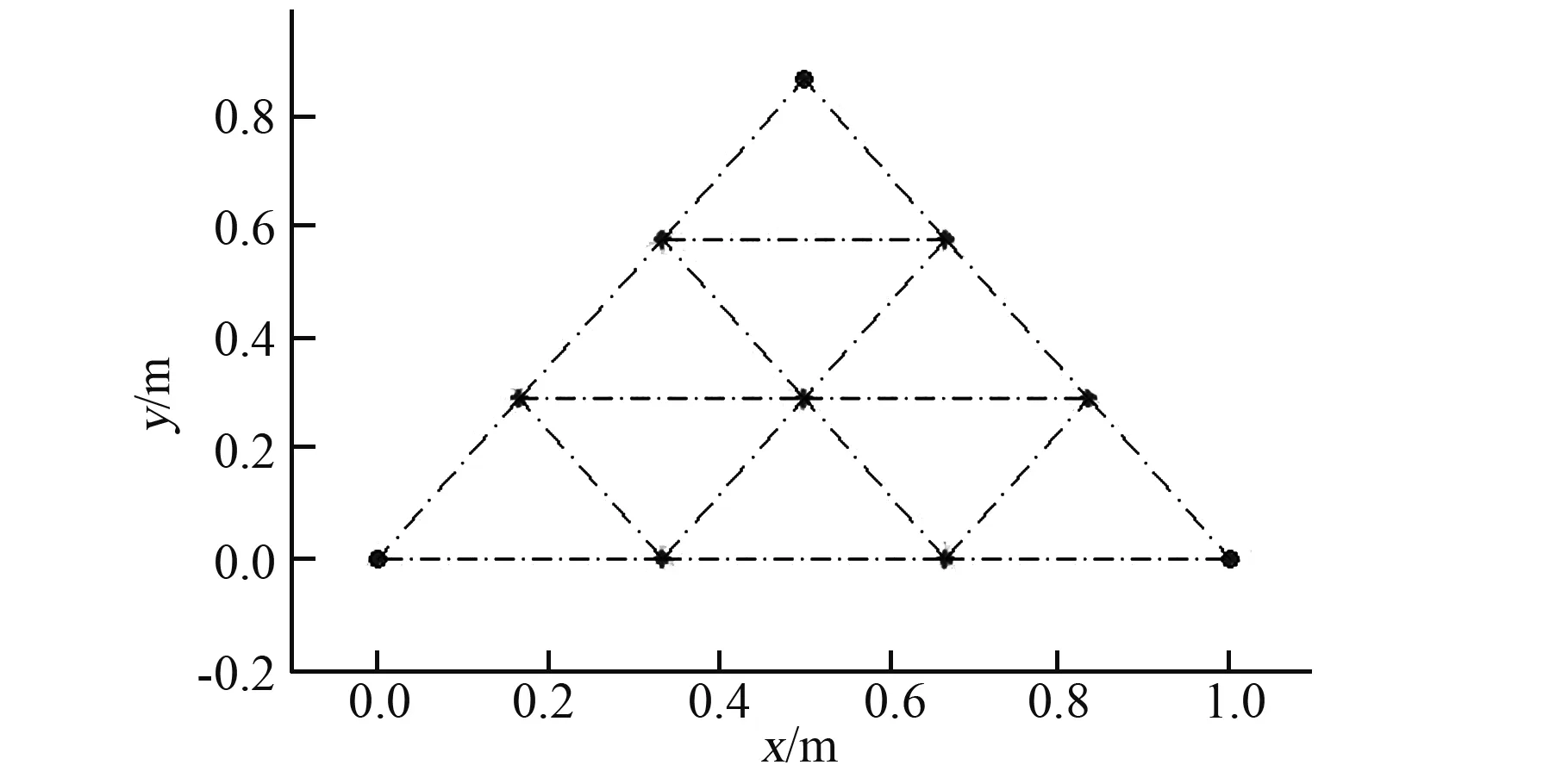
图1 多机器人的目标网形状Fig.1 Target shape of multi-robot network
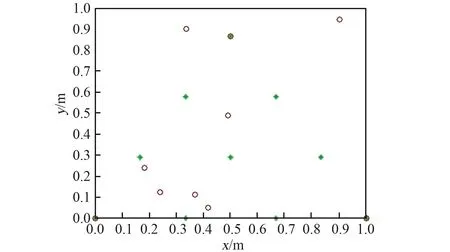
图2 多机器人的初始估计位置Fig.2 Initial position guess of multi-robot network

图3 分布式梯度方法的定位结果Fig.3 Localization result of distributed gradient based method
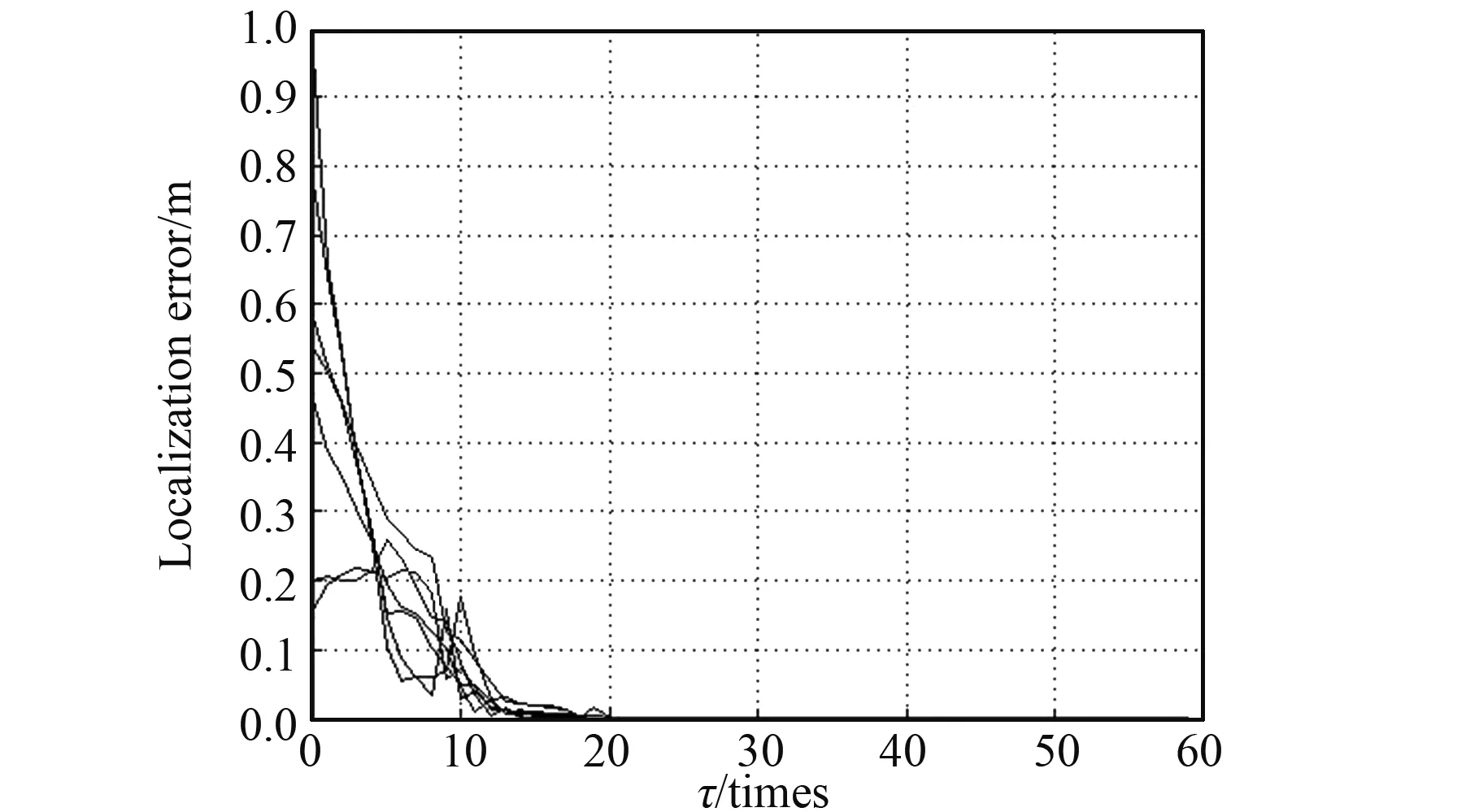
图4 每个机器人的定位误差随时间的收敛性能Fig.4 Convergence performance of robots in the network
实际中机器人的初值估计可能存在多种情况。这里分别考虑机器人初始位置估计在给定区域[1 m×1 m]内的均匀分布和以目标位置为均值、标准差为0.4 m的高斯分布2种情况,每种条件进行100次蒙特卡洛仿真,算法性能比较结果如表1所示。设置不同的步长计算迭代次数t,t=10、20、40、80。 算法性能从误差收敛的迭代次数、定位误差和计算时间来评价。结果表明,算法分布式计算步长需要的迭代次数对定位误差和算法误差收敛迭代次数的影响很小。但算法的计算时间与分布式步长计算的内部迭代次数相关,随着与内部迭代次数的增加近似成比例变化。因此,在分布式计算步长过程中,t较小就可以满足步长一致的要求。
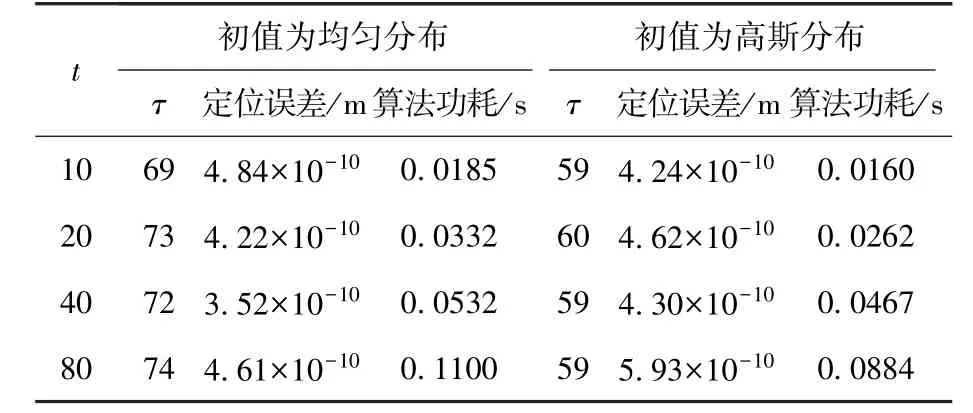
表1 不同初始估计条件的性能比价Table 1 Algorithm performance under different initial position guesses
图5展示了上述对比试验中,机器人从初始估计的位置(图中星号)收敛到目标网络定位节点(图中三角号)的轨迹。图5(a)假设初始位置为均匀分布,适合对未知环境机器人初始部署。从收敛轨迹可见,机器人移动的步长较大,而收敛有震荡情况发生。图5(b)假设初始位置估计为高斯分布,收敛轨迹步长比较小而且速度较快,适合当机器人定位误差较大时重定位的情况。这也表明,初始位置估计误差较大时,算法需要较长时间,但最终会收敛到全局的最优值。
在上述仿真试验中,重点考虑了静态的多机器人系统,即当多个机器人随机分布在给定区域,利用有限的测距信息,可以快速确定每个机器人在整个网络中的定位。对移动的多机器人网络而言,如果可以保持彼此的通信畅通,利用该方法,机器人可以运动到指定目标位置,形成期望的网络拓扑结构。这样图5中的收敛轨迹就演变成移动机器人的运动轨迹。

图5 不同初始位置估计条件下机器人位置收敛轨迹Fig.5 Convergent trajectories of robots in the network under two initial position guesses
5 结论
该分布式定位算法可以分为一致步长迭代和机器人位置更新2个阶段。仿真验证表明当多机器人网络拓扑为刚度图时,该算法具有全局收敛性,即对机器人初始位置估计值不敏感。由于只需少数几次迭代即可获得一致步长,算法在满足分布式运算的同时还可满足计算效率和定位精度的要求。另外,对多个移动机器人形成指定队列的问题,该算法从初值估计到精确定位的收敛轨迹可以作为移动机器人的运动轨迹,因此该方法可以扩展应用到多移动机器人网络。
