用转移反应研究6He奇特核体系的光学势

杨 磊，林承键,3,*，贾会明，马南茹，王东玺，杨 峰，徐新星，孙立杰，温培威，钟福鹏,3，孙浩瀚，张焕乔

(1.中国原子能科学研究院 核物理研究所，北京 102413； 2.国防科技工业抗辐照应用技术创新中心，北京 102413； 3.广西师范大学 物理科学与技术学院，广西 桂林 541004)

核-核相互作用势是研究核反应机制过程中需首先确定的最基本的物理量。由于核-核相互作用非常复杂，在实际应用中通常采用唯象的光学模型势进行描述[1-3]。众所周知，光学势对于核的结构非常敏感，因此奇特核体系的光学势必定会表现出与紧束缚体系不同的特征。这引起了人们的极大关注，是目前低能核反应领域的研究热点之一[4-6]。

通常，抽取光学势参数最简单有效的方法是通过测量体系的弹性散射角分布，然后通过光学模型计算拟合实验结果来抽取该体系的光学势参数。但对于放射性核束，由于受到目前放射性束流装置所能提供束流的种类、强度和品质的限制，使实验很难达到较高的精度，这对抽取可靠的光学势参数造成了很大的困难。针对这种情况，提出了利用转移反应抽取奇特核体系光学势的方法，即利用稳定核束的转移反应作为探针，通过拟合转移反应角分布抽取出射道奇特核体系的光学势参数[7]。这种方法具有如下的优点：1) 可利用现有的高强度、高品质的稳定束流，使实验达到相对较高的精度，如统计、能量和角度精度等；2) 转移反应的末态可布局到不同的激发态，这非常有利于进行势参数能量相依性的研究，同时也使针对某一核态进行专门的研究成为可能。基于该方法，在北京HI-13串列加速器上进行了多个体系的转移反应测量，以研究出射道奇特核体系光学势性质[8-13]。本文将介绍通过7Li的单质子转移反应研究出射道晕核6He体系光学势。

1 唯象的光学模型势

在20世纪40年代末，壳模型的成功使人们认识到：由于泡利不相容原理的限制，核子在核内与其他核子交换能量和动量的概率较自由核子小得多，可把核子看作是在核内其他核子的平均场中作独立粒子运动。为将吸收效应也包含在内，引入复数势，用虚部来描述吸收。入射粒子在靶核的平均复势阱中运动，当入射粒子和靶核发生相互作用后，一部分被散射(透射或反射)，称为势弹性散射或形状弹性散射，而另一部分被吸收。其中描述入射粒子与靶核相互作用的复数势U(r)通常可写成式(1)形式， 这种形式的势函数U(r)即被称为光学模型势，简称光学势。

U(r)=V(r)+iW(r)

(1)

根据核力的性质、核结构的相关知识以及微观光学势研究的一些定性结论，可将光学势U(r)表达成某种函数形式，其中包含一些待定参数，然后通过调节这些参数使得由光学模型计算的截面和角分布等均能较好符合实验数据，则使用这种方式所确定的光学势称为唯象光学势。

在研究唯象光学势的过程中，通常将光学势的实部和虚部分成深度和形状两个因子。则式(1)可写为：

U(r)=VfV(r)+iWfW(r)

(2)

光学模型本身并未对光学势的形状给出具体的限定，因此只要选取适当的复数势，使得计算结果能准确描述实验测量结果即可。由于光学势基本上表示平均场，而核力又是短程力，因此势阱应与核物质分布有相同的形状，即在核中心部分有一平台区，边缘部分为弥散层，相互作用在核外迅速趋近于零。符合这些特点的形状因子，最常用的是Woods-Saxon形状因子：

f(r)=(1+exp(r-r0(Ap+At)1/3/a0))-1

(3)

式中：Ap、At分别为弹核和靶核的质量数；r0、a0分别为作用势的半径和弥散参数，为可调参数。本文所讨论的唯象光学势均采用Woods-Saxon形状因子。

光学模型发展至今，经过几十年的深入研究，已总结出关于紧束缚体系光学势参数的一些系统学规律，如紧束缚体系的光学势在势垒附近表现出阈异常现象[14]，即在垒下能区，随着入射能量的降低，虚部势深度减小，并很快趋于零；而实部深度则在势垒附近剧烈变化，呈钟罩型。实部的势深度V(r;E)可写成随能量缓慢变化的V0(r;E)以及与由虚部变化而产生的动力学极化势ΔV(r;E)之和的形式，即：

V(r;E)=V0(r;E)+ΔV(r;E)

(4)

ΔV(r;E)与虚部势深度W(r;E)的关系可由色散关系描述：

(5)

其中，P为积分主值。色散关系是因果律在稳定体系中的自然体现，通常称为Kramers-Kronig关系，描述了波穿过介质时的色散效应。

2 转移反应抽取光学势的理论基础

对于一般核反应a+A→b+B，其反应的微分截面可表示为：

(6)

其中：μi和μf分别为初态和末态的折合质量；ki和kf分别为初态和末态的波矢；Tfi为跃迁矩阵T的矩阵元〈kf|T|ki〉。

式(6)通常不能严格求解，一般采用各种近似方法求解薛定谔方程。关于碰撞问题的近似方法，最常用的是玻恩近似，即把剩余相互作用看作微扰。在平均场U的作用下，初态和末态粒子的波函数需用U作用下的扭曲波来表示，由此得到扭曲波玻恩近似(DWBA)。在DWBA的计算中，T矩阵可写成如下形式：

(7)

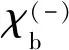
对于转移反应，其反应示意图如图1所示。在用式(7)计算转移反应跃迁幅度T的过程中，形式因子〈B,b|V|A,a〉包含了所有核结构的信息，其中最重要的是谱因子S和转移粒子x在核中的波函数。计算过程中需考虑如下相互作用。

1) 散射态a与A的相互作用，可用入射道光学势Ua-A描述；

2) 束缚态a内部的相互作用，即a内部b与x的相互作用，可用束缚态势Ub+x描述；

3) 散射态b与B的相互作用，可用出射道光学势Ub-B描述；

4) 束缚态B内部的相互作用，即B内部A与x的相互作用，可用束缚态势UA+x描述。

因此，转移反应的理论微分截面是相互作用势Ua-A、Ub+x、Ub-B和UA+x的泛函：

dσ/dΩ=f(Ua-A,Ub+x,Ub-B,UA+x)

(8)

由式(8)可知，当转移反应的角分布dσ/dΩ已知，并且Ua、UB、UA和Ub中任意3个已知，即可通过拟合转移反应角分布抽取唯一未知的光学势。通常，束缚态的作用势Ua和UB可通过再现x粒子分离能的方法得到。因此在入射道光学势UA已知的情况下，即可通过拟合转移反应A(a,b)B的角分布来抽取出射道b+B体系的光学势。

3 光学势参数的灵敏性测试

为验证该方法的可靠性，进行转移反应角分布对出射道光学势参数敏感性的测试，确定转移角分布能否对出射道的势参数产生足够的约束[15]。以208Pb(7Li,6He)209Bi为例，分别从文献中选择一套能描述其入射道和出射道的光学势参数，并计算其转移反应角分布。将入射道的势参数固定，以一定的步长单独改变出射道光学势中的每个参数(V、rV、aV、W、rW、aW)，重新计算体系的转移反应角分布，并相互比较，观察角分布随出射道各势参数的变化而改变的幅度，即转移角分布对出射道势参数的灵敏性。Elab(7Li)=42.55 MeV下的计算结果如图2所示。

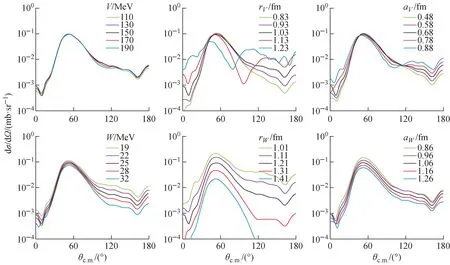
图2 208Pb(7Li,6He)209Bi在Elab(7Li)=42.55 MeV下的 转移角分布随出射道6He+209Bi体系光学势参数的变化Fig.2 Variation of angular distribution of 208Pb(7Li,6He)209Bi with optical potential parameters of 6He+209Bi system in exit channel at Elab(7Li)=42.55 MeV

由测试的结果可见，在入射道体系光学势参数固定的情况下，改变出射道体系的相互作用势参数会引起理论转移角分布一定程度的变化。且计算结果对光学势的作用半径和弥散参数非常敏感，能充分体现出核的结构对该反应产生的影响。

另一方面，相比于弹性散射测量抽取光学势，转移反应方法由于需克服库仑作用而发生核反应，因此能对核势提供更强的约束，从而可抽取得到更高精度的势参数。这一优势在垒下能区将更显著：当粒子入射能量低于库仑位垒时，由于强的库仑排斥作用，弹散角分布对核势并不敏感，而转移反应方法由于受到转移反应角分布的进一步约束，将更有利于抽取高精度的光学势参数。为验证此，分别计算208Pb(7Li,6He)209Bi在垒下能量Elab(7Li)=21.20 MeV下的转移反应角分布以及6He+209Bi体系在相应能量(Ec.m.(6He)=14.34 MeV)下的弹性散射角分布。角分布随6He+209Bi实部和虚部光学势深度的变化结果如图3所示。

为便于比较，引入灵敏性参数S，其定义为：

S=dσ/dV(W)

(9)

其中：dσ为最背角处微分截面的相对变化；dV(W)为实部和虚部势深度的相对变化。根据计算结果，转移反应的实部和虚部的灵敏性参数分别为0.021和0.093，而弹散相应的值分别为0.001 7和0.033。可见，相比于传统的弹性散射方法，在统计误差相同的情况下，转移反应方法抽取得到的实部和虚部势深度的精度可分别提高12倍和3倍。

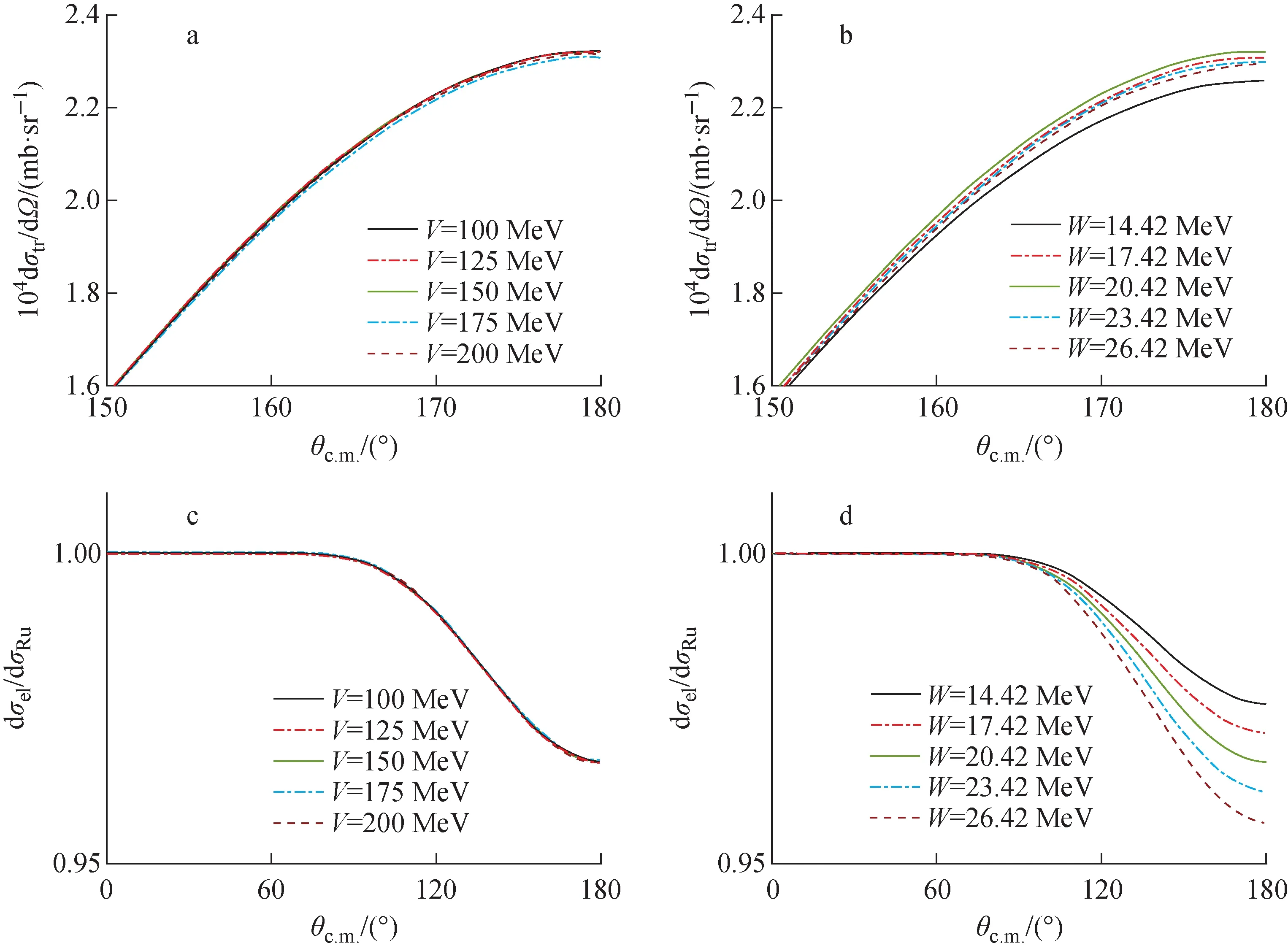
a——208Pb(7Li,6He)209Bi在垒下能量Elab(7Li)=21.20 MeV下的转移反应角分布 随出射道6He+209Bi体系光学势实部势深度的变化； b——208Pb(7Li,6He)209Bi在垒下能量Elab(7Li)=21.20 MeV下的转移反应角分布 随出射道6He+209Bi体系光学势虚部势深度的变化； c——6He+209Bi体系在相应能量(Ec.m.(6He)=14.34 MeV)下的弹性散射角分布随实部势深度的变化； d——6He+209Bi体系在相应能量(Ec.m.(6He)=14.34 MeV)下的弹性散射角分布随虚部势深度的变化图3 角分布随6He+209Bi体系实部和虚部光学势深度的变化Fig.3 Variation of angular distribution with potential strength V and W of 6He+209Bi system

4 晕核6He体系光学势

基于北京HI-13串列加速器，分别在近库仑位垒能区完成了7Li+11B、63Cu、208Pb的弹性散射和单质子转移反应角分布11B(7Li,6He)12C[9]、63Cu(7Li,6He)64Zn*[11]、208Pb(7Li,6He)209Bi*[10,12-13]的测量。通过拟合弹性散射数据，抽取得到入射道体系的光学势参数，并作为转移反应计算的输入参量。对转移反应角分布，分别利用DWBA和耦合反应道(CRC)方法进行拟合，以抽取出射道晕核6He体系的光学势参数。所有计算通过FRESCO[16]程序完成。

4.1 6He+12C体系

在入射能量Elab(7Li)=9.85、13.30、18.30、23.30、28.30 MeV下测量了11B(7Li,6He)12C的单质子转移反应角分布，结果如图4所示，图中CRC和DWBA的拟合结果分别用实线和虚线表示。在CRC的拟合框架中，主要考虑了非弹激发到7Li前3个激发态的耦合效应以及基态和每个激发态的自耦合，同时还包括了两步的单质子转移过程。其中7Li的激发态采用集体模型描述，即用形变的作用势描述激发态的耦合效应。抽取得到的6He+12C体系的实部和虚部势深度的能量相依性如图5所示。由于所测量能区远高于6He+12C体系的库仑位垒(质心系下约3 MeV)，因此无法观测到位垒附近光学势深度的剧烈变化。利用线性函数对实部和虚部势深度的能量相依性分别进行线性拟合，结果示于图5，图中，虚线和实线分别为对DWBA和CRC方法得到的势深度进行线性拟合的结果。

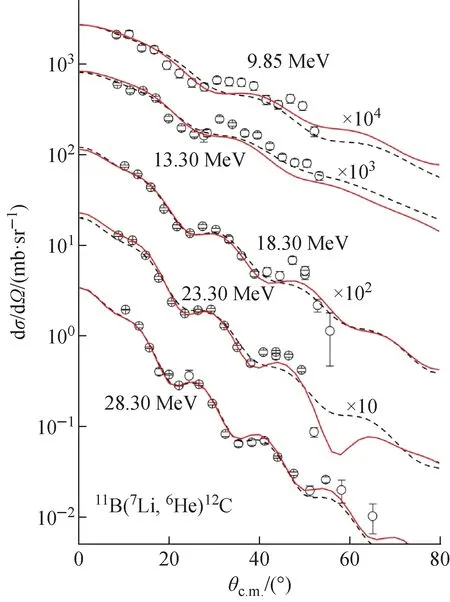
图4 11B(7Li，6He)12C体系的转移反应角分布Fig.4 Angular distribution of transfer reaction 11B(7Li, 6He)12C

图5 实部(a)和虚部(b)势深度 随6He+12C体系质心系能量变化的情况Fig.5 Depths of real (a) and imaginary (b) potentials with reaction energy of 6He+12C system

为验证利用这种转移的方法抽取得到的光学势的可靠性，利用得到的势参数重新计算了目前文献中已有的6He+12C体系的弹性散射角分布。在已有的弹散数据中，Elab(6He)=18 MeV[17]的数据恰好与本工作中Elab(7Li)=9.85 MeV的单质子转移反应所对应的6He+12C体系的能量一致，可用于直接验证势参数的可靠性。由转移反应抽取得到的出射道光学势是一种有效的相互作用势，包含了各种动力学极化势的成分。因此根据此套参数，可直接利用简单的光学模型计算6He+12C体系的弹性散射角分布。计算结果与实验数据的比较示于图6。由结果可见，仅在θc.m.≤40°的前角区域，理论计算的角分布与实验数据符合得较好。之外的区域存在着明显的相位和幅度的差异。造成这种差异的原因可能在于：对于轻体系，结构效应明显，平均场理论可能并不能准确描述轻体系的相互作用；轻体系的弹性散射角分布有明显的振荡结构。尤其对于轻的奇特核体系，由于破裂、转移等各种反应道的存在，使情况更复杂。简单的光学模型计算很难对弹性散射角分布的结构给出令人满意的描述，进一步的CRC计算可能会改善理论结果与实验数据符合的程度。

空心圆为实验数据[17]，实线和虚线分别为利用 CRC方法和DWBA方法抽取得到的光学势计算的结果图6 6He+12C体系的弹性散射角分布Fig.6 Angular distribution of elastic scattering of 6He+12C system

4.2 6He+64Zn体系

束流7Li的能量分别为Elab(7Li)=12.67、15.21、16.33、23.30、27.30、30.96 MeV，得到的63Cu(7Li,6He)64Zn*转移反应角分布如图7所示。在CRC的计算中，考虑了7Li第一激发态以及63Cu第一、第二激发态的耦合效应。

抽取得到的6He+64Zn体系的光学势实部和虚部的势深度的能量相依性分别如图8a、b所示。可见，在所研究的能量范围内，DWBA和CRC方法得到的势参数均在一常数附近变化，且这两种方法得到的结果存在明显差异。由于HI-13串列加速器可提供的7Li束流能量的限制，无法在垒下能区进行测量，因此未观测到在位垒附近光学势参数剧烈变化的现象。为验证所得结果的可靠性，利用所得势参数重新计算了目前文献中已有的6He+64Zn体系在Elab(6He)=10.0、13.6 MeV的弹散角分布数据，结果分别如图8c和d所示。可见，只有通过CRC方法得到的势参数才能重现实验数据。对于反应体系63Cu(7Li,6He)64Zn*，其入射道为7Li+63Cu，均为奇A核，且7Li基态有较大的四极矩，而63Cu在满壳层外存在1个2p3/2态的价质子，较易激发。这些均会对转移道产生较强的耦合效应。在CRC方法的计算过程中，由于考虑了弹核和靶核激发态的耦合效应，可得到准确可靠的出射道光学势。

4.3 6He+209Bi体系

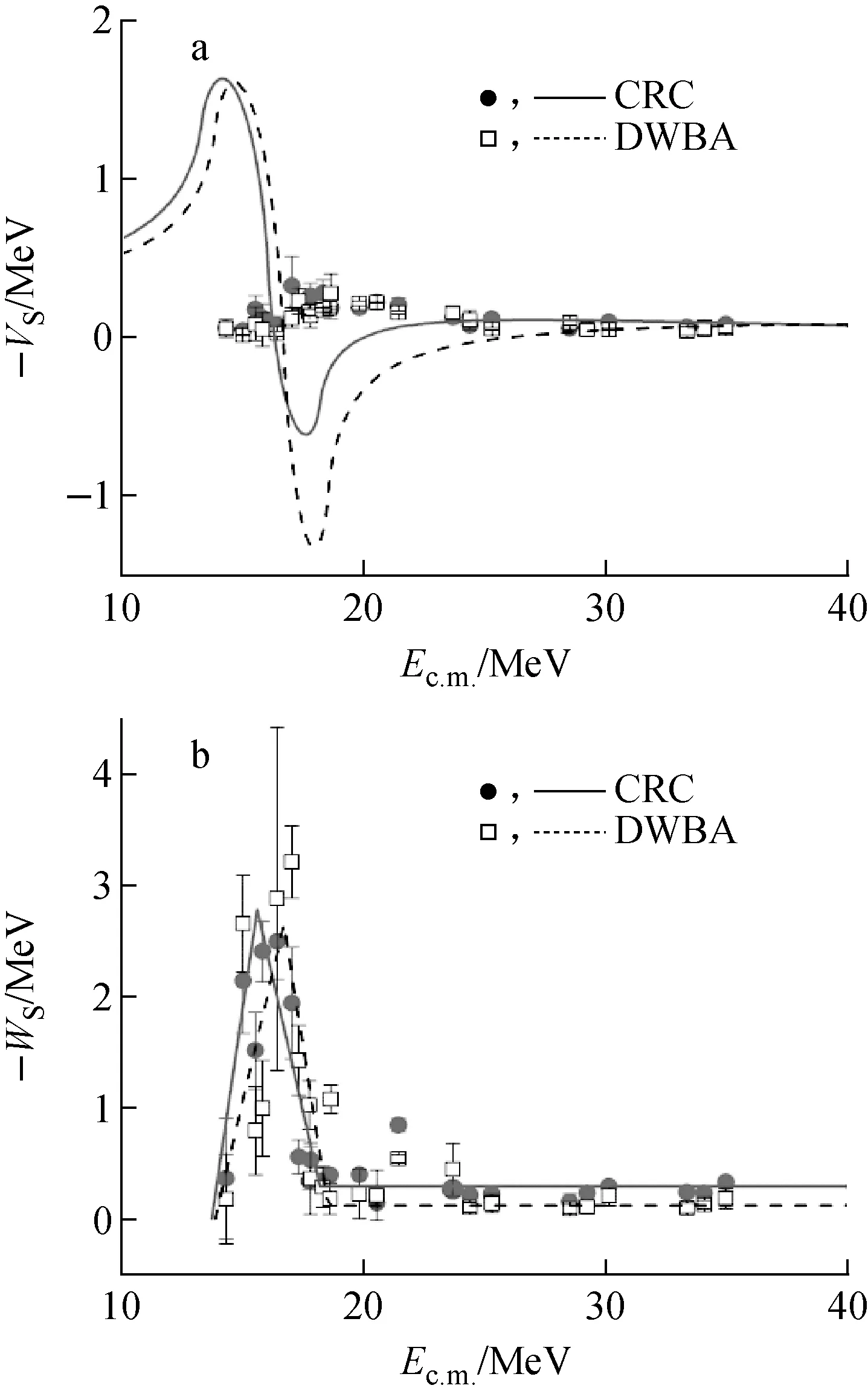
图9 6He+209Bi体系实部(a)和虚部(b) 势深度在灵敏半径13.5 fm处的能量相依性Fig.9 Energy dependence of real (a) and imaginary (b) potentials at sensitivity radius of 13.5 fm for 6He+209Bi system

在近库仑位垒区域测量了208Pb(7Li,6He)209Bi*转移反应角分布，Elab(7Li)分别为21.20、24.30、25.67、28.55、32.55、37.55和42.55 MeV，转移角分布结果见文献[10,12-13]。由CRC和DWBA方法抽取得到的6He+209Bi体系的实部和虚部势深度随体系能量的变化如图9所示，图9b中实线和虚线分别为对CRC和DWBA结果的分段线性拟合，图9a中相应曲线则是根据图9b中的拟合结果由色散关系预言的实部变化趋势。CRC计算过程中考虑了7Li前3个激发态以及单中子转移的耦合道效应。由结果可见，CRC和DWBA方法得到的势参数基本相同，表明对于该重体系，耦合道效应可能并不显著。利用抽取得到的势参数重新计算6He+209Bi体系的弹性散射角分布，并与文献[19-20]中的实验数据进行比较，结果如图10所示。可见，CRC和DWBA方法得到的势参数均能较好重现实验数据，验证了势参数的可靠性。

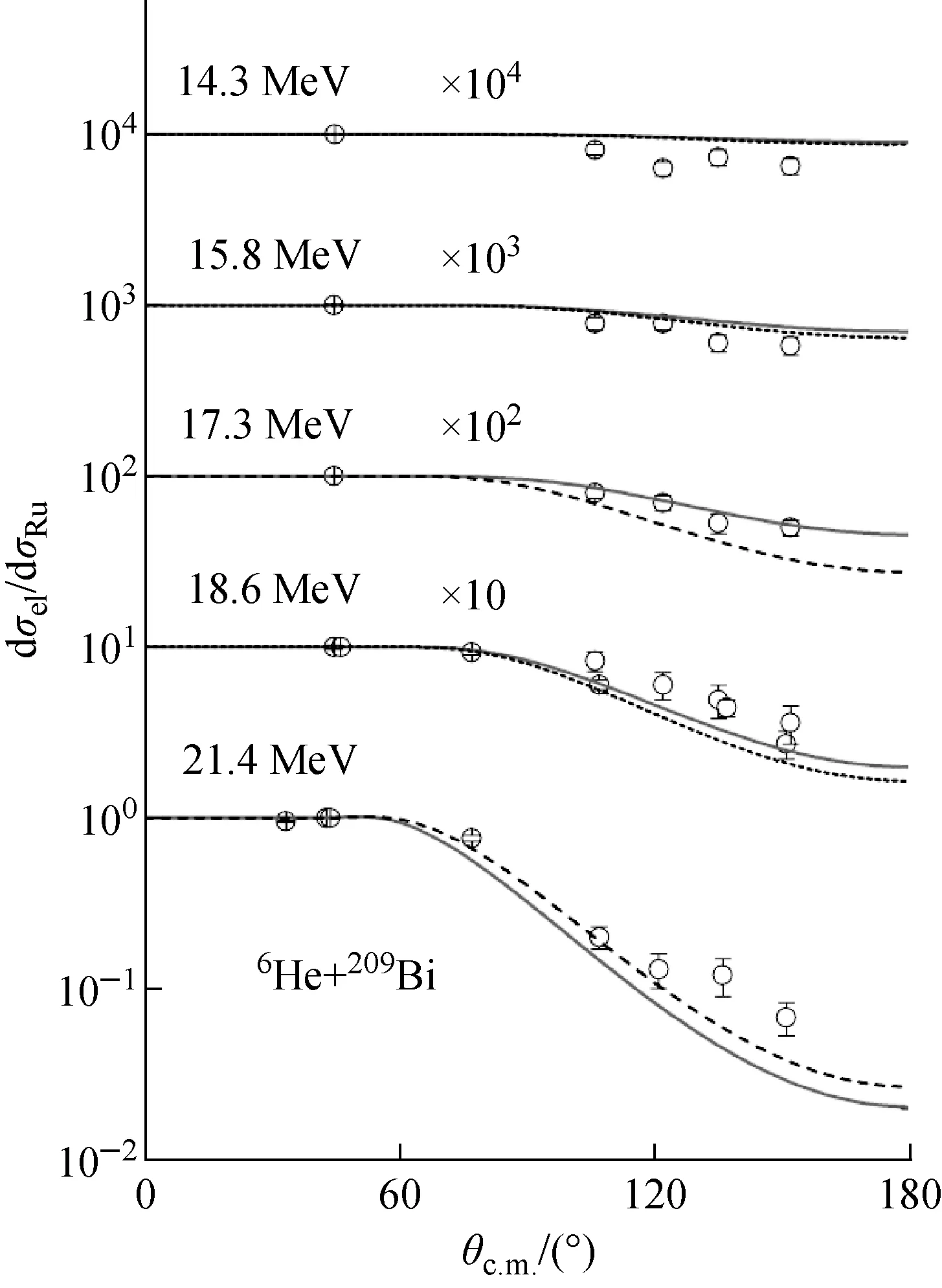
空心圆为取自文献[19-20]的实验数据，实线和虚线 分别为CRC和DWBA方法抽取得到的光学势的计算结果图10 6He+209Bi体系弹性散射角分布Fig.10 Elastic scattering angular distribution of 6He+209Bi system

为考察势参数的能量相依性，利用分段线性函数对CRC和DWBA得到的虚部势深度分别进行了线性拟合，结果如图9b所示。可见，随着体系能量的降低，虚部势深度在位垒附近呈上升趋势，表现出了反常的阈异常现象[21]。随着能量的进一步降低，虚部深度迅速下降，直至为0。由此可得到6He+209Bi体系的反应阈能为0.68VB，这是首次在晕核体系中观测到了反应阈能。相比于紧束缚体系16O+208Pb(阈能为0.93VB)[14]和稳定弱束缚体系6Li+144Sm(阈能为0.81VB)[22]，6He+209Bi体系的低反应阈能进一步说明了晕核6He更松散的物质分布。根据虚部的变化趋势，基于色散关系[23]计算了实部势深度的能量相依性，结果如图9a中曲线所示。可见，色散关系预言的实部深度变化趋势与实验结果并不相符。色散关系由于其因果律的基础，通常作为普适的关系而广泛应用于核物理领域。这一结果则提供了色散关系不适用于奇特核体系的有力证据。其潜在的物理原因还需进一步深入研究[12-13]。

5 结果与讨论

通过DWBA和CRC方法对实验得到的11B(7Li,6He)12C、63Cu(7Li,6He)64Zn*和208Pb(7Li,6He)209Bi*体系的单质子转移反应角分布进行拟合，抽取得到了上述3个反应体系出射道6He+12C、6He+64Zn和6He+209Bi晕核体系的唯象光学势参数。该方法抽取得到的出射道光学势是有效的相互作用势。而相比于DWBA方法，CRC方法通过求解耦合道方程可进一步排除入射道对于出射道的各种耦合效应。

为验证所抽取光学势的可靠性，利用抽取得到的光学势计算了目前文献中已有的相应体系的弹性散射角分布，通过与实验结果的对比可得到以下结论。

1) 对于轻体系6He+12C，由于其自身的结构效应，弹性散射的角分布振荡结构明显。由CRC和DWBA两种方法抽取得到的光学势参数都不能准确描述大角度处的弹性散射角分布的结构。在所得结果的基础上，进一步的CRC计算可能会改善理论结果与实验数据的符合程度。

2) 对于中重体系6He+64Zn，由CRC方法抽取得到的势参数能较好地重现文献中的弹性散射数据；而DWBA方法得到的势参数则无法准确描述该体系的弹性散射角分布结构。其原因可能来自于入射道的影响。在CRC方法的计算过程中，考虑了弹核和靶核激发态的耦合效应，可得到准确可靠的出射道光学势。

3) 对于重体系6He+209Bi，由于入射道为7Li+208Pb体系，208Pb为近球形核，非常稳定，并且平均场可很好地描述重体系的相互作用。因此，在近垒及垒上能区，由DWBA和CRC方法抽取得到的光学势都能较好重现相应体系的弹性散射角分布以及体系的总反应截面。

另一方面，由于受到北京HI-13串列加速器所能提供的7Li束流能量的限制，仅在6He+209Bi体系中进行了近垒及垒下能区的测量，从而能对该体系光学势参数在位垒附近的变化规律进行研究。结果表明，虚部深度在位垒附近表现出反常的阈异常现象；在深垒能区，随着能量的进一步降低，虚部深度迅速减小至0。同时，基于虚部的变化规律，色散关系无法重现实部势深度的变化趋势，表明色散关系对于该晕核体系并不适用。这非常类似于包含负折射率材料的系统[24]。其可能的物理原因如下。

1) 色散关系是由Kramers-Kronigs[25]关系推出，其理论基础为柯西留数定理。该定理的必要条件为在实轴上只能有有限个独立的奇点。对于核反应体系，这些奇点就对应于分立的核态。而对于弱束缚体系，由于反应过程中存在连续态，因此可能并不能严格满足色散关系的数学要求。

2) 从实验数据中提取得到的是定域的唯象光学势，而实际的核-核相互作用势是非定域的。由定域光学势近似非定域的相互作用势会引入额外的能量依赖关系[26]。显然，这种额外引入的能量相依性不需满足色散关系。

3) 不论是弹性散射方法还是转移反应方法，只能确定某区域内的光学势，即所谓的光学势的灵敏区域。弹性散射和转移反应均为周边作用过程，因此抽取得到的光学势只敏感于相互作用的尾巴部分。实验[27]表明，即使用1 GeV的高能质子轰击12C靶核，由于强吸收效应，仍无法探测到核势的中心部分。因此，无法得知外围的光学势参数能否准确重构出强吸收半径内部的波函数。而只有能重现所有空间范围内波函数的势参数才能满足色散关系的要求。因此，只敏感于外部灵敏区域的唯像光学势可能并不需要遵守色散关系的约束[28]。

6 小结

本文介绍了利用转移反应方法抽取出射道奇特核体系光学势参数方法的理论基础，并对该方法的可靠性进行了论证。利用该方法在北京HI-13串列加速器上完成了11B(7Li,6He)12C、63Cu(7Li,6He)64Zn*和208Pb(7Li,6He)209Bi*单质子转移反应的测量，并通过CRC和DWBA方法对转移角分布进行拟合，抽取了出射道晕核6He+12C、64Zn和209Bi体系的光学势参数。

由于受加速器所能提供的7Li束流能量的限制，仅对208Pb(7Li,6He)209Bi*在垒下能区进行了测量。根据光学势参数的能量相依性，清楚观测到了6He+209Bi体系的虚部势深度在库仑位垒附近的反常阈异常现象，并首次在深垒能区看到虚部深度随能量降低而下降的趋势，从而抽取了6He+209Bi体系的反应阈能。同时，该结果也首次证明了基于因果律的色散关系并不适用于该晕核体系。其深层的物理原因还需进一步研究。

利用转移反应抽取出射道奇特核体系光学势的方法为研究奇特核体系的光学势提供了全新的思路。已在轻体系11B(7Li,6He)12C、中重体系63Cu(7Li,6He)64Zn*和重体系208Pb(7Li,6He)209Bi*中验证了该方法的可行性。该方法可进一步推广到其他体系，以对奇特核体系的光学势性质进行深入系统的研究。