基于LMS-PNN算法在心音识别与预测中的应用

周克良 王佳佳

（江西理工大学电气工程与自动化学院，赣州，341000）

引 言

据相关数据统计，全世界每年约1750万人死于心脏病，占总死亡人数的30%。每年心脏病和中风幸存者至少有2000万人，且多数存在复发和死亡的风险。中国每年大约有260万人死于心血管疾病，死亡人数居世界第2位。据世界卫生组织统计，到2020年中国每年因心血管疾病死亡人数将达400万人。对于心脏健康状况的监测成为国内外相关领域较重视的问题。而心脏最直观的监测对象便是心电图和心音，医生可以根据心电图判断心脏跳动的频率是否正常，而心音可辅助判断心脏是何处异常或损坏，及时了解病人的病情，挽救病人的生命。因此研究心音的识别与预测具有重要意义。

心音的杂音是一组历时较长、频率及振幅均不同的振动，既可与心音分离，也可连续，或完全覆盖心音。目前对于心音降噪分析采用的是经验模态分解（Empirical mode decomposition，EMD）、小波包分析、Mel频谱倒谱系数等方法，这些算法可以提取出异常心音与正常心音的特征数据，并根据这些特征数据，以及心音的训练样本，采用BP神经网络、支持向量机（Support vector machine,SVM）、径向基函数（Radial basis function,RBF）神经网络等进行训练，达到识别及其预测的效果。文献[1]利用主成分分析对心音特征进行降维,采取自组织映射神经网络进行聚类分析,并对各种异常和正常心音进行分类识别。文献[2]在EMD的基础上,引入了单通道奇异值分解(Singular value decomposition,SSVD)方法,在心音降噪方面取得了良好效果。文献[3]将概率神经网络（Probabilistic neural network，PNN）引入电控发动机故障诊断，诊断结果无误。

PNN具有较强的泛化性和实用性，故本文对传统PNN进行优化，用于心音数据分类。运用Matlab 2013a软件，采用LMS-PNN对心音数据去噪，提取降噪后的特征数据进行训练，降低了传统PNN的误差，提高了识别的准确率，改善了心音预测效果。

1 心音的降噪与特征值提取

由于心音信号的短时平稳性[4]，本文采用最小均方(Least mean square,LMS)方法[5]进行心音去噪。对于心音信号的时间序列x(n),利用窗函数分帧后得到第i帧语音信号xi(m)，帧长设置为200，对每帧心音信号做离散傅里叶(Discrete Fourier transform,DFT)变换后可得

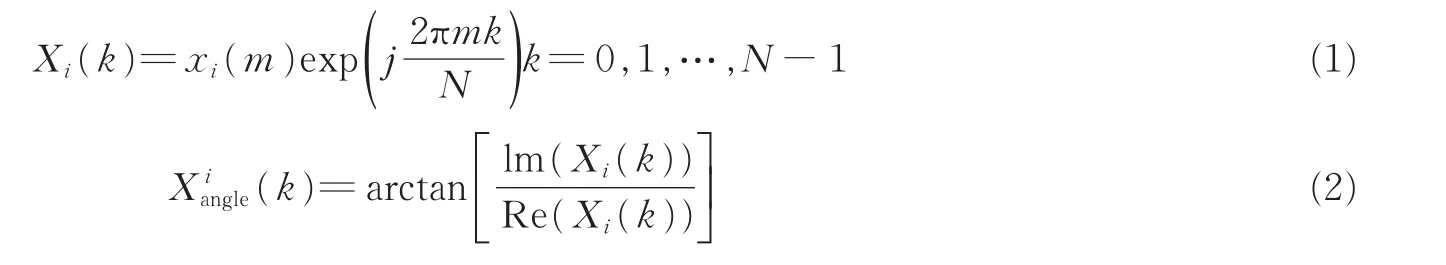
式中Xiangle为第i帧的相角。

式中：NIS为帧数，D(k)为无话段的平均能量。

式（4）为谱减公式，其中a和b为常数，a为过减因子，b为增益补偿因子为谱减后的时间系列。

然后提取降噪后数据的特征值，本文提取降噪心音的短时自相关系数和短时能量谱密度[6-8]。对降噪后的x(k)分帧后，每帧的短时自相关函数为

采用Matlab软件中的pwelch函数求得心音每帧的短时能量谱密度，并保存计算数据。

2 PNN识别与预测

PNN于1989年由Specht博士首先提出，是基于统计原理的神经网络模型，在分类功能上与最优贝叶斯分类器等价。PNN的实质是基于贝叶斯最小风险准则发展而来的一种并行算法[9,10]，由输入层、模式层、求和层和输出层（决策层）组成。第1层为输入层，用于输入特征数据，将数据传递跟隐含层；模式层为径向基层，计算输入向量与中心之间的距离，并返回一标量。向量x输入到模式层，模式层中第i类模式的第j神经元所确定的关系式为

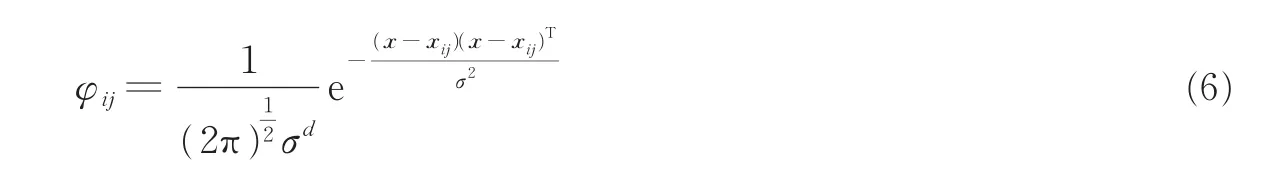
式中：i=1,2,…,M,M为训练样本总类数；d为样本空间数据维数；xij为第i类样本的第j个中心。求和层把隐含层中属于同一类的神经元的输出做加权平均

式中：vi为第i类别的输出，L为第i类神经元的个数。输出层取求和层中最大的一个作为输出的类别

输入层的向量先于加权系数相乘，由输入RBF计算

3 实验结果与分析

本文采集的心音信息来自赣州某医院的临床数据，包括：心室舒张期额外音（正常）心室舒张期额外音（严重）、收缩早期喀啦音（严重）等心音。运用LMS算法对上述3种心音进行降噪与分析，采样频率为44100Hz，采样信号和采样数据分别以wav和mat格式保存。采用本文的观察数据与观察图像可得：IS为0.4 s,a取值为10，b取值为0.01。通过LMS降噪后，降噪结果如图1、2所示。图1为心室舒张期额外音（正常）的带噪心音波形，图2为经LMS滤波后心室舒张期额外音（正常）的去噪波形，由图1、2对比可知，LMS算法滤波明显去除了心室舒张期额外音（正常）的杂音。

再对去噪后的心音进行特征提取、短时域时域处理和短时域频域处理，得到各心音的短时自相关数据及短时功率谱密度，将得到的数据以mat格式保存。图3、4分别为心室舒张期额外音（正常）正常自相关系数及短时功率谱密度图。

图1 带噪心音波形Fig.1 Noisy heart sound waveform

图2 LMS谱减后的心音信号波形Fig.2 Heart sound signal waveform after LMS spectrum reduction

对于PNN，输入层输入短时自相关数据及短时功率谱密度数据，加上模式层输入训练数据，共有40000个训练样本数据，其中心室舒张期额外音（正常）样本数据10000个，心室舒张期额外音（严重）样本数据10000个，收缩早期喀啦音（严重）样本数据10000个和测试数据10000个。输出层将输出数据进行等级划分：“1”代表心室舒张期额外音（正常），“2”代表心室舒张期额外音（严重），“3”代表收缩早期喀啦音（严重）。当模式层中出现错误的心音数据时，PNN通过计算心音特征数据与各个心音等级的匹配度。训练过程中出现相似度不强时，会直接剔除错误数据，而不会对其进行分类。实验数据验证结果如图5～7所示。

图3 正常心音自相关系数Fig.3 Normal heart sound autocorrelation coefficient

图4 正常心音的短时功率谱密度图Fig.4 Short-time power spectral density map of normal heart sounds

图5 LMS-PNN的测试准确率Fig.5 Test accuracy rate of LMS-PNN

图6 LMS-PNN和传统PNN的预测结果Fig.6 Prediction results of LMS-PNN and traditional PNN

本文将所采集的心音信号数据转换100×100的矩阵，在这个矩阵中，利用双重循环语句，将不同行列之间心音信号数据进行模型编号，并采用LMS-PNN算法对模型数据测试训练。由图5可得，模型1，5所采用的数据测试准确率比较低，在多次模型的训练结果下，LMS-PNN通过不断自我学习与反馈，总体模型测试结果呈现升上趋势，其测试正确率在模型6～9保持稳定，准确率可达96.66%。

图7 LMS-PNN的训练时间Fig.7 Training time of LMS-PNN

图6为30个测试样本集的测试数据，由实验数据验证可得，LMS-PNN对心音数据分类的准确性高于传统PNN，准确率高出10%。

由图7仿真结果可知，LMS-PNN神经网络算法在数据矩阵不同行列之间所组成的10个数据模型中不断进行自我学习与训练，其训练时间由0.155 s逐渐稳定至0.062 s，实验结果证明，LMS-PNN神经网络算法在心音测试模型中效果表现良好，训练时间呈现逐步缩短到稳定的趋势训练时间短、不易产生局部最优，收敛速度比较快，而且其分类准确率也较高。

对于上述仿真结果，LMS-PNN神经网络算法的平滑因子N是LMS-PNN算法的关键。令平滑因子N分别取值为20和2，其测试集预测结果对比如图8所示。图8（a）是N=20时LMS-PNN算法得到的预测结果；图8（b）是N=2时LMS-PNN算法得到的预测结果。由图8可知，N=20时，LMS-PNN预测准确率为90%；N=2时，LMS-PNN预测准确率为93.33%，准确率高出了3.33%。不同的平滑因子得到的结果也有所不同，因此选取合适的平滑因子能提高预测准确率。由表1可知，当平滑因子N=10时，LMS-PNN算法的预测准确率最高，为最优值。

图8 LMS-PNN的预测结果（N=20，2）Fig.8 Prediction results of LMS-PNN(N=20 and N=2)

表1 平滑因子N的影响Tab.1 Influence of smooth factor N

4 结束语

测试心音通常会受到噪声影响，LSM-PNN算法运用LSM方法进行去噪，采用双门限法估计出无话帧即噪音帧IS的值，调整参数a，b的值，观察数据及其波形，优化去噪效果；然后使用PNN，采用贝叶斯决策理论对心音的信号进行区分与预测。对LSM-PNN算法，无论分类问题多么复杂，只要有足够多的训练数据，均可保证获得贝叶斯准则下的最优解。