基于ResNet的稳健语音DOA估计算法
2019-10-30郭业才刘力玮顾弘毅
郭业才 刘力玮 顾弘毅
(1.南京信息工程大学电子与信息工程学院,南京,210044;2.南京信息工程大学滨江学院,无锡,214105)
Key words:DOA estimation;array imperfection;generalized cross-correlation;residual network
引 言
波达方向(Direction of arrival,DOA)估计是阵列信号处理的重要方向之一,其广泛应用在远程自动语音识别[1],电话会议和自动摄像机转向[2]等方面。然而,当阵列流型存在缺陷时,要得出准确的DOA估计是很困难的。因此,需要一种可以在缺少阵列流型误差的先验信息时进行鲁棒DOA估计的方法。
传统DOA估计方法主要可以分为:(1)子空间方法,例如多重信号分类(Multiple signal classification,MUSIC)[3]和借助旋转不变技术估计信号参数技术(Estimating signal parameters via rotational invariance techniques)[4];(2)广义互相关(Generalized cross-correlation,GCC)[5]和最小二乘法(Least squares,LS)[6];(3)信号同步方法,例如基于联合可控响应功率和相位变换(Steered response power using the phase transform weight,SRP-PHAT)方法[7]和多通道互相关(Multichannel cross-correlation coefficient,MCCC)方法[8];(4)脉冲响应的盲识别方法,例如自适应特征值分解(Adaptive eigenvalue decomposition,AED)算法[9]和独立分量分析方法[10];(5)基于l1范数惩罚的稀疏信号表示方法[11];(6)基于模型的方法,例如最大似然法[12]。上述方法计算成本高,并且依赖对阵列流型的假设。
针对上述传统方法存在的问题,近几年出现了基于神经网络的DOA估计方法[13,14]。这些方法只对语音信号做简单的特征处理,如计算信号的协方差矩阵或广义互相关,利用神经网络完成信号特征到DOA结果之间的映射关系。这些方法将DOA视作分类问题,没有对信号做过强的假设,一定程度上克服了传统方法的缺点,取得了良好的DOA估计效果。
近年来,深度卷积神经网络在图像处理研究中取得一系列突破。网络深度是深度卷积网络的一个重要参数,更深的网络能强化特征提取和非线性映射能力,但堆叠过深会产生梯度爆炸、消失的问题。尽管此问题可以通过增加初始归一化[15]和中间归一化层解决,但随着网络深度的进一步增加,拟合精度变饱和后迅速退化。残差卷积网络[16]一定程度上解决了这一问题,通过更深的网络提高拟合精度。
结合以上背景,本文在文献[13]的基础上,将残差网络(Residual network,ResNet)应用于声源DOA估计中,并根据神经网络数据驱动,不依赖阵列流型的特点,提出了一种在阵列误差条件下基于ResNet的稳健语音DOA估计算法。与其他基于神经网络的DOA估计方法不同,该算法没有将DOA估计视作分类问题,使用基于欧几里德距离的代价函数对DOA进行回归建模。将整个定位范围分若干个子区间,使用一个基于神经网络的深层分类器对信号分类,根据分类结果选取对应子区间数据训练得到的ResNet对信号DOA估计,即为本文的基于ResNet的缺陷阵列DOA语音估计。
1 阵列模型
1.1 理想阵列模型
设均匀线型麦克风阵列有M个阵元,阵元间距为d,每个阵元都是相同的全向麦克风,远场信号以θ入射。假设噪声为与入射信号独立的高斯白噪声,均值为0,方差为σ2,则阵列在k时刻的输出为

式中:a(θ)为M×1维的阵列流型矩阵,s(k)为1×K维的目标信源复振幅矢量,n(k)为M×K维的加性噪声复矢量。

1.2 考虑误差的阵列模型
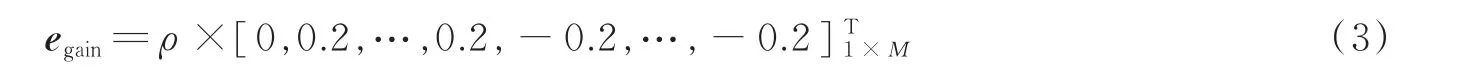
式中:ρ∈[0,1]为控制阵列误差程度的系数,M为阵元个数。相位误差矢量为

考虑2种典型的阵列误差,增益、相位误差以及麦克风位置误差。本文使用的增益误差矢量为
位置误差矢量为

式中,d为均匀线阵的间距。加入阵列误差的阵列流型为

式中:δ(⋅)为控制误差是否存在的参数,IM为M×M的酉矩阵,diag(⋅)为对角线设置为给定矢量的对角矩阵。虽然式(6)的阵列流型与实际情况相比简化了很多,但在利用神经网络进行DOA估计的过程中整个系统没有用到有关阵列误差的先验信息,这里的阵列流型仅用来生成仿真数据,因此神经网络DOA估计的稳健性并不是针对特定的阵列误差,可以认为这里的简化是合理的。
2 基于ResNet的语音DOA估计
基于广义互相关的传统DOA估计算法都存在过强的假设,例如不存在混响、噪声与信号之间互不相关、阵列模型为均匀线阵或圆阵等。因此,极端环境下经典DOA估计算法往往会有较大偏差甚至失效。针对此问题,本文使用ResNet完成基于GCC的DOA估计结果的映射。由于ResNet的卷积结构,将输入特征以一对麦克风对的GCC为一行,堆叠成矩阵,卷积时可以获取不用麦克风对之间的特征信息。
传统的基于GCC的DOA估计算法需要先通过GCC估计时延,再通过时延得到信号入射角度。通过时延估计入射角的过程依赖于阵列流型,因此当阵列模型存在与理想模型偏差较大时,DOA估计误差会明显增大。而神经网络由数据驱动,DOA估计的过程不依赖于阵列流型,仍然可以在阵列模型误差条件下获得良好的DOA估计效果。
2.1 特征提取
选取GCC-PHAT作为输入特征的基础。先将麦克风阵列接收的语音信号分为长0.1 s的语音帧,对每帧语音做GCC-PHAT处理。根据阵列模型参数和环境参数对每帧语音尺寸裁剪,得到子特征矩阵。最后,将所有子特征矩阵加权求和得到语音信号的特征矩阵。
2.1.1 GCC-PHAT
设阵列模型中的第m和n个麦克风阵元接收的信号经过离散采样后分别为xm(k)和xn(k),则

式中:nm(k),nn(k)分别为两个麦克风接收信号中的噪声;am,an为信号幅度衰减因子;τm,τn为声源信号传播到2个麦克风所用的时间采样点数量;s(k)为声源信号。
忽略混响的影响,xm(k)和xn(k)的相关函数为

将式(7,8)代入式(9)得
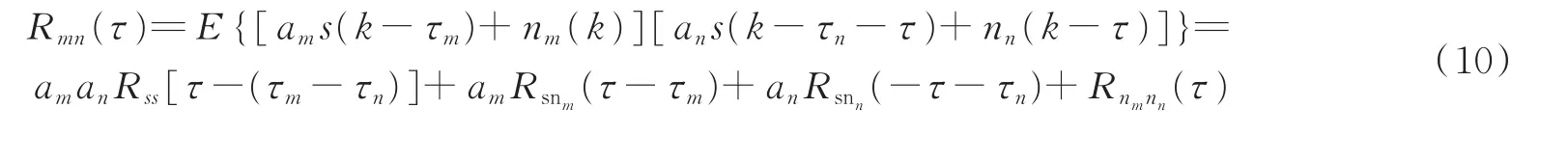
设s(k),nm(k)和nn(k)互不相关,则式(3)可写为

式中,τmn=τm-τn,Rss(τ)为声源s(k)的自相关函数。
当τ-τmn=0时,Rmn(τ)取最大值。因此可由Rmn(τ)的最大值估计两个麦克风阵元接收信号的时延采样点τmn。
由互相关函数和互功率谱的关系,可得

GCC通过在式(4)加上加权函数,得

式中:Wmn(n)为加权函数,Gmn(n)为2个信号的互功率谱。PHAT加权函数其效果等价于白化滤波。
2.1.2 特征矩阵构建
设均匀线阵由M个阵元,阵列间距为d,阵元麦克风之间两两组合总共有m=C2M对麦克风对,对每0.1 s信号计算GCC并做相位变换(GCC-PHAT),2个麦克风阵元之间的最大间隔为(M-1)d,阵元之间存在的最大时延为(设声速为c),设入射信号采样率为fs(单位Hz),代表时延的GCC波峰一定会出现在中间n=fs×τ个点中。因此,输入矩阵维度为m×n。
由于语音信号的特点,在对语音信号分帧处理时可能有一些非语音帧,为了更强的鲁棒性对每个语音帧加权[16]

式中:om为第m个语音帧,D为GCC矩阵的元素数,om(d)为GCC矩阵的第d个元素,|·|为取绝对值,a为控制参数,若a=0则获得GCC向量的平均值。使用大的a可有效降低静音帧对GCC矩阵的影响。
2.2 深层分类器结构
深层分类器是一个神经网络结构,如图1所示。分类器输入为基于GCC的特征矩阵,分类器的前向传播为
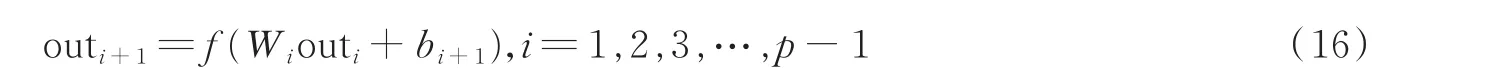
式中:outi为第i层神经元的输出,Wi为第i层与第i+1层之间的神经元连接权重,bi为第i+1层的神经元偏置,p为神经网络层数,f(⋅)为神经元激活函数。out1为网络输入,即基于GCC-PHAT的特征矩阵,outp为网络的输出,即信号所在的子区间编号。
输出层的激活函数取softmax函数,损失函数为

式中:m为样本个数,n为网络输出层神经元个数(与子区间个数相等),1{⋅}为示性函数,y(i)为第i个样本的标签,θTjx为输出层第j个神经元的输入。再通过误差的反向传播,更新整个分类器网络的权重。

图1 深层分类器的结构Fig.1 Structure of deep classifier
2.3 ResNet网络结构
ResNet与其他卷积神经网络(Convolutional neural network,CNN)的区别在于其残差结构。残差结构的典型结构如图2所示,设期望映射为H(x),则残差结构的期望映射为F(x)=H(x)-x,最终的输出结果为F(x)+x。
F(x)+x通过外加求和单元的前馈神经网络实现,增加求和单元不会增加参数,整个网络可以按照原来的反向传播算法进行训练。
改良的ResNet将批归一化层(Batch normalization,BN)和激活层(Relu)的位置由非线性层的后面转移到前面[17],改良的ResNet结构,如图3所示。图中除第一个卷积块以外所有卷积块都由BN、Relu和卷积层依次连接得到。

图2 残差单元结构Fig.2 Residual element structure
每个残差求和层(Sum)前有2个3×3的卷积块,每次卷积时加上尺寸为1的Pad保持尺寸不变。每4次残差以后的一个卷积块选用3×3的卷积核,加1尺寸的Pad,以2为步长对输入进行卷积,缩小尺寸1/2,通道数加倍。缩小3次后在经过一个卷积块将尺寸收缩到1×1,通过全连接层,送入Loss层。
网络使用基于欧几里德距离的损失函数为

式中:yi为第i个样本的标签,Yi为第i个样本特征输入网络后网络的输出,m为样本个数。
2.4 系统性能指标
采用均方根误差(Root mean square error,RMSE)来比较本文算法、基于多层感知器(Multi-layer perceptron,MLP)的算法和LS-TDOA算法的准确性和稳定性。RMSE定义为

式中:R为测试使用的样本数,θS为信号的真实入射角度,θˆrS为DOA系统得出的估计入射角度。
3 实验和仿真
3.1 仿真与实验条件
仿真实验条件,如图4所示,房间尺寸为5.5 m×3.3 m×2.3 m,均匀阵列放置在高度为1 m位置,阵列的阵元间隔为0.2 m,阵元数量为8个。房间的四面墙壁和天花板反射系数为0.95(普通石灰墙),地板的反射系数为0.90。
数据集声源信号选取纯净的语音信号,入射角度以0.1°遍历各个分组的定位范围,按7∶3的比例随机抽取训练集和测试集。数据集规模约为4.5万个。将音响设置在参考阵元的不同角度作为声源,实验数据由一个8阵元线型麦克风阵列采集,阵元间距为0.2 m。

图3 ResNet结构Fig.3 Structure of ResNet

图4 仿真条件示意图Fig.4 Schematic of simulation conditions
3.2 结果分析
3.2.1 子区间个数对DOA性能的影响
划分的子区间个数对系统性能的影响,如图5所示。图中横坐标代表测试信号的信噪比,纵坐标为估计结果与实际结果之间的均方根误差。图5表明,随着P的增大,每个子区间的宽度减小,用于DOA估计的ResNet的泛化压力随之降低,因此系统性能提升。当P大于6以后,继续增大P对DOA系统的提升不再明显。
3.2.2 阵列误差对DOA估计性能的影响
阵列误差的DOA估计性能的影响,如图6所示。图中横坐标为控制阵列误差大小的参数ρ,纵坐标为估计结果与实际结果之间的均方根误差,3条曲线分别为MUSIC算法、基于MLP的语音DOA估计算法[13]和本文提出的基于ResNet的语音估计算法。可以看出MUSIC算法虽然在ρ较小时性能更强,但随着阵列流型与理想流型相差增大,估计性能显著下降。基于MLP的语音估计算法虽然表现出了一定的稳健性,但由于其结构简单,泛化能力不够强,性能仍有一定下降。基于ResNet的DOA估计算法由于增加了分类器结构,降低了泛化压力,又得益于ResNet比MLP更强的建模能力,对阵列误差的稳健性更强。
3.2.3 信噪比对性能的影响
信噪比对系统性能的影响,如图7所示。图中将本文算法、基于MLP的DOA估计算法以及MUSIC算法在不同信噪比下的性能进行对比,图中实线为使用约3000个仿真测试信号在随机角度位置的测试结果,图中虚线为使用约100个语音信号在消声室3个固定角度的测试结果。
由图7表明,在高信噪比时几种算法之间的差异不是很大,但信噪比在10 dB以下时,MUSIC算法性能显著下降,而2种基于神经网络的DOA算法仍能有效工作,且本文提出的算法性能更佳。由于实验器材的电噪声和测量时引入的不可避免的误差等原因,几种算法的RMSE均有所上升,但本文算法在低信噪比下的优势仍十分明显。
4 结束语
本文首次使用ResNet解决了阵列误差条件下语音信号的定位问题。通过增加分类器结构,降低了神经网络的泛化压力。利用ResNet强大的非线性映射能力,在普通石灰墙房间和消声室环境中均取得了良好的效果,证明了基于ResNet的DOA估计算法对阵列误差的稳健性。
但在极低信噪比下,深度神经网络仍出现了一定程度的过拟合现象,如果扩大数据集的同时使用更深的网络结构可能会获得更好的效果。
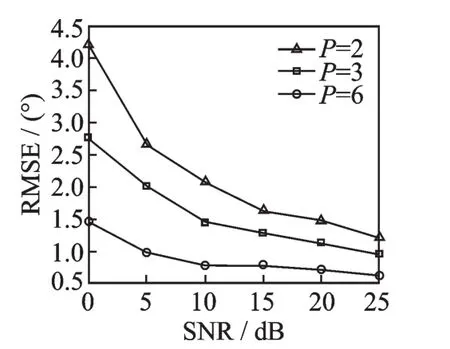
图5 划分的子区间个数对系统性能的影响Fig.5 Influence of the number of subintervals on system performance

图6 阵列误差对DOA估计性能的影响Fig.6 Effectof array error on DOA estimation performance
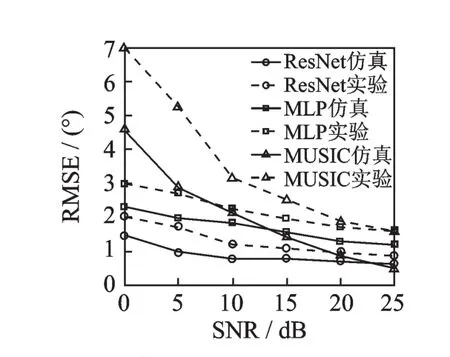
图7 信噪比对系统性能的影响Fig.7 Influence of signal to noise ratio on system performance
