基于深度特征与局部约束掩膜的相关滤波跟踪算法

2019-10-30王译萱吴小俊

数据采集与处理 2019年5期

王译萱吴小俊

（江南大学物联网工程学院，无锡，214122）

引言

目标跟踪作为计算机视觉中的重要研究方向，在安防监控、无人驾驶和智慧城市等方向有着广泛的应用[1-3]。跟踪的主要目的是在连续的视频序列中建立和更新目标的动态表观模型，以此为依据获得运动目标的运动参数和轨迹等，从而满足军用以及民用需求[4]。

历经30年的研究与发展，跟踪算法的性能有了广泛的提高，目前算法主要分为生成学习和鉴别学习两大类[5]。生成学习跟踪算法对当前帧目标区域建模，在下一帧采取寻找与模型最为相似区域，以此确定目标位置[6]。早期的相关工作主要有粒子滤波算法[7]、均值漂移跟踪算法[8]和稀疏表示等跟踪算法[9]等。生成学习类算法的主要局限在于过分关注目标本身的外观信息，忽略了目标外观具有动态性和随机性等特点，因此不能准确把握目标外观动态信息，无法实现鲁棒跟踪。为了在跟踪过程中引入背景信息，研究人员设计出了鉴别学习类跟踪算法，此类算法将跟踪问题转为分类或回归问题，将目标信息作为正样本，背景信息为负样本训练分类器，将目标从图像背景中分离出来，以此实现跟踪。近年来，基于鉴别学习类的相关滤波跟踪算法成为了研究热点并受到了广泛关注，该方法的设计初衷是学习得到一个对目标响应高而对背景响应低的滤波器。通过滤波器模板和搜索区域的响应值，判断目标位置。Bolme等[10]首先提出了输出误差最小平方和跟踪算法(Minimum output sum of squared error，MOSSE)，通过频率域特性缓解了训练过程中样本数量不足的问题。随后，Henriques等[11]在MOSSE算法的基础上利用循环结构扩充了训练样本集，提出了循环结构跟踪算法（Circulant structure kernel，CSK）。在此基础上，Henriques等[12]进一步将原有的单通道灰度特征（Gray scale）扩展为多通道的方向梯度直方图特征（Histogram of oriented gradient，HoG），同时将核计巧（Kernel trick）加入到滤波器求解过程中，提出核化相关滤波跟踪算法（Kernelized correlation filter，KCF）。为了解决跟踪过程中目标的尺度变化问题，Danelljan等[13]提出了多尺度相关滤波跟踪算法(Discriminative scale space tracking,DSST)，该方法针对目标存在的尺度变化问题，将单独的尺度滤波器加入到算法中，通过尺度采样和尺度回归的方式计算目标的尺度变化。为了将目标的颜色信息引入跟踪过程中，Danelljan和Bertinetto等分别提出了使用颜色名称特征的自适应颜色属性实时跟踪算法（Adaptive color accurate tracking,ACAT）[14]以及基于颜色直方图独立模板的相关滤波跟踪算法（Complementary learners for real-time tracking,Staple）[15]。颜色特征（Color name,CN）在目标发生形变、遮挡时具有良好的鲁棒性，因此后续的相关滤波算法在特征提取阶段多数都采用了HoG特征结合CN的方式增加跟踪结果的可靠性。近年来大量优秀算法将深度特征引入相关滤波跟踪框架中[16-18]，与传统特征相比，深度特征包含更加丰富的语义信息，对目标产生的旋转、平移和缩放等具有较好的鲁棒性[19,20]。尽管深度特征的提取过程较为复杂，但随着计算机硬件的不断发展，目前已经可以通过图形处理器（Graphics processing unit,GPU）实现深度特征的运算，因此对基于深度特征的目标跟踪算法还有着重要的研究意义和价值。

本文在经典相关滤波算法基础上，提出了基于深度特征与局部约束掩膜(Local constrained mask,LCM)的相关滤波跟踪算法。在滤波器的学习过程中，利用二值矩阵作为局部约束掩膜对滤波器边缘能量分布进行裁剪，对模板边缘与测试图像之间产生的响应进行抑制，提升了滤波器的鉴别能力；将通过ResNet50深度网络提取到的深度特征加入跟踪算法中，利用深度特征学习目标表观模型时，将目标图像通过旋转、翻折和高斯模糊3种方式扩充样本数量，提升目标模板的表达能力，最终采用深度特征结合传统特征的组合形式，提高了复杂背景下跟踪结果的准确性和鲁棒性。

1 多通道相关滤波算法

相关滤波跟踪算法通过在目标周围建立采样区域，采集训练样本实现滤波器的训练。通过滤波器和测试图像之间产生的响应值判断目标的当前位置，响应值最高的位置通常为候选目标位置[5,11]。在采样的过程中，相关滤波算法对目标样本进行循环移位操作快速生成大量训练样本，进而通过离散傅里叶变换(Discrete Fourier transform,DFT)，将滤波器的求解过程转换到频率域进行，其求解过程可视作优化函数ε和求解滤波器h，即

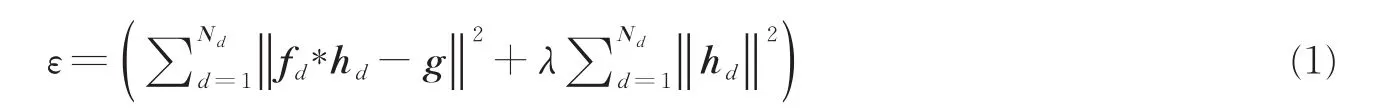
式中：hd为待求解的滤波器，*表示循环卷积操作，fd为提取到的目标特征，Nd为特征通道总和，g为对应的高斯响应，其峰值位于中心，λ为正则项系数，防止模型过拟合。对式(1)进行离散傅里叶变换,可将循环卷积操作变为频域中的点乘,减少卷积耗时，即

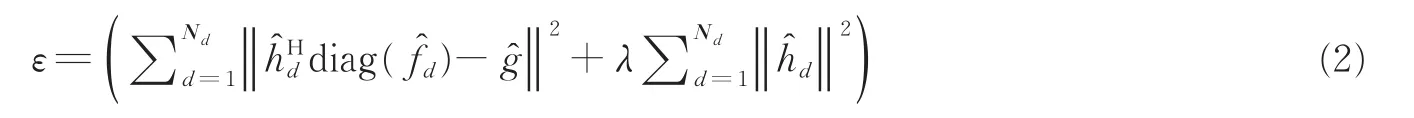
式中：fˆd和hˆd分别为fd和hd的傅里叶变换，hˆHd代表hˆd的复数共轭形式，对式(2)的求解为标准的岭回归问题，因此相关滤波器hd在频域内有闭环解(Close-form solution)，即

式中：⊙表示频率域中的点乘操作，式(3)的详细推导过程请参阅文献[5]。

考虑到目标在跟踪过程中的外观变化，学习得到的滤波器需要在线更新，更新过程通常采用滑动平均的方式，因此在第t帧视频序列中相关滤波器hˆ的更新公式为

式中：η为模板更新速率，t为当前帧数。

在新一帧的目标检测过程中，根据上一帧目标的位置，提取测试图像z和学习得到的滤波器hˆ进行相关操作，得到当前帧的目标响应，响应值最高的位置为目标位置，即

式中：R(z)为当前帧的响应值，F-1表示傅里叶逆变换。

2 多通道相关滤波算法的改进

在多通道相关滤波算法的基础上，本文提出基于深度特征与LCM的相关滤波跟踪算法，利用学习得到的二值矩阵作为LCM对滤波器进行处理，消除滤波器模板的边缘信息，实现扩大目标搜索区域的同时，降低循环样本带来的边界效应，获得更高的跟踪精度。

2.1 LCM的相关滤波跟踪算法

2.1.1 局部掩膜

鉴别学习类跟踪算法的主要难点在于训练分类器时的训练样本过少，传统相关滤波算法为了增加训练样本的数量，对目标周围建立一个搜索区域，以区域内的图像作为原始样本，在空间域内采用循环移位的方式生成大量虚拟样本，搜索区域越大，获得的训练样本数越多[20]。尽管该方式为算法提供了更多样本，但这些虚拟样本因受边界效应的影响，弱化了分类器的鉴别能力，对算法的跟踪精度造成影响，因此传统方法只能将目标搜索区域控制在相对较小的范围内。为了有效解决上述问题，近年来的改进算法,如空间正则化相关滤波器(Spatially regularized correlation filters,SRDCF)[21]和鉴别性空间通道可靠性相关滤波跟踪算法(Channel spatial reliability discriminative correlation filter,CSRDCF)[22]通过抑制滤波器模板的边缘信息，实现了目标搜索区域的扩大，有效提升了跟踪结果的准确性和鲁棒性。

在此基础上，本文提出了一种新型的掩膜操作，通过二值矩阵作为LCM,在频域与滤波器进行点乘操作，即

式中，m为二值矩阵，其大小与与目标搜索区域大小相同，训练时可由测试视频序列中第1帧给定的目标位置和大小求得，hm则表示与m点乘后的滤波器，点乘的过程中对目标区域取1，保留目标区域模板信息，模板边缘区域取0，消除滤波器模板边缘的能量，达到抑制边界效应的目的，在后续的跟踪过程中，为保证m的准确性，其大小始终与第一帧(Ground-truth)得到的结果保持不变。此外，由于本文提出的掩膜操作作用于滤波器模板，而并非直接作用于原始图像，因此在训练阶段不会因目标运动产生干扰，造成跟踪结果下降。与使用颜色直方图前景掩膜的CSRDCF算法相比[21]，本文提出的二值矩阵掩膜无需获取输入图像的颜色直方图特征，因此减少了算法耗时。此外，本文根据目标区域大小生成的掩膜具有更大的空间范围，在跟踪的过程中可以有效减少因使用感受野较大的深度特征而产生的信息丢失问题，提升算法的跟踪精度。本文提出的二值矩阵掩膜示意图如图1所示。

图1 二值矩阵掩膜示意图Fig.1 Schematic diagram of binary matrix mask

2.1.2 优化过程

将式(6)作为约束条件加入损失函数式(1)中，即

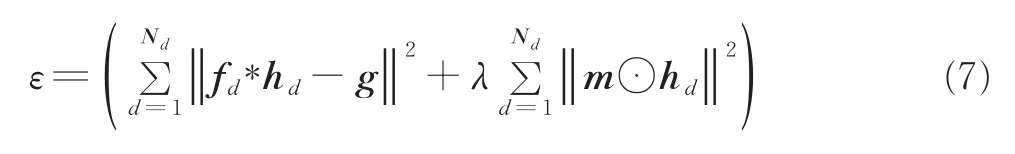
采用增广拉格朗日乘子法(Augmented Lagrange method,ALM)[23]对式(7)进行优化求解,优化过程中需引入松弛变量h'd=hd，即

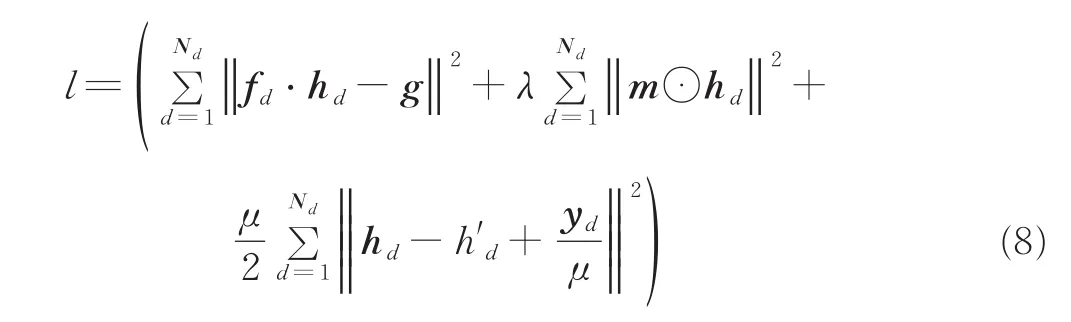
式中：yd为拉格朗日乘子，μ为惩罚系数。式(7，8)的详细推导过程请参阅文献[22]。对式(8)采用交替方向乘子法(Alternating direction method of multipliers,ADMM)[24],将式(8)分为2个子问题，交替求解，即

式(9)需要利用帕萨瓦尔定理(Parseval’s theorem)[18]转换到频域内求解,即

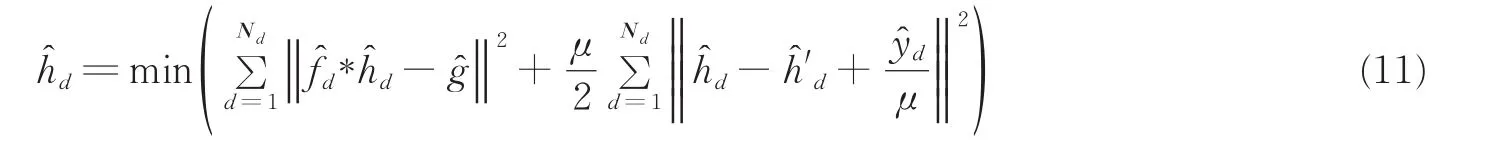
对式(10)中h'd和式(11)中的ˆd分别求偏导数，得到2个变量的闭环解，即

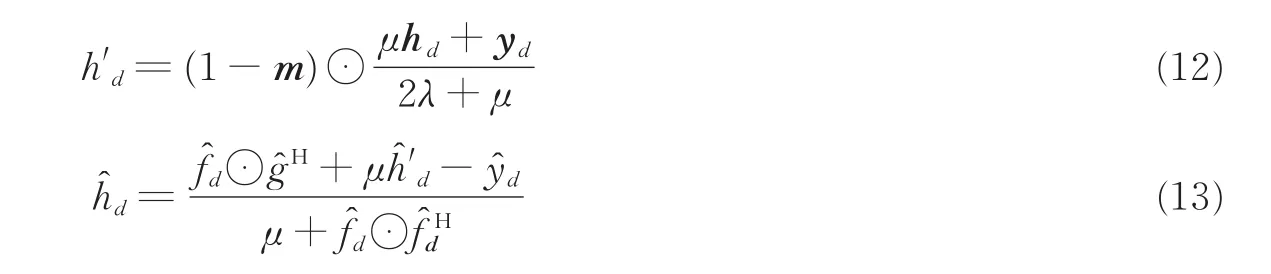
利用式(12，13)进行迭代求解，随着迭代次数的增加，松弛变量h'd的值会无限逼近于hd，因此本文将选取作为滤波器最终训练模板。

yd和μ在迭代的过程中需要更新，更新公式为

2.2 深度特征的引入以及训练样本扩充

目前大部分针对相关滤波跟踪的改进算法在特征提取阶段均采用HoG结合CN的形式，这种传统特征组合在跟踪速度上具有一定优势，但在目标发生遮挡、尺度变化、背景杂乱和形变以及复杂背景下表现较差[14-20]。为了进一步提升算法性能，本文在HoG和CN的基础上[21]，将通过深度网络提取到的ResNet50深度特征引入跟踪算法中，深度特征是网络通过大数据自动学习得到的特征，其中包含大量参数。近些年来，深度特征被广泛应用在图片检索和分类等任务中[19]，与传统特征相比，深度特征具有较大的感受野，鲁棒性较好[25]。为了获取更为鲁棒的深度特征，本文选择ResNet50网络中第4个卷积块的res4ex层的输出作为输入特征，该输出共包含1024个特征图谱。与浅层的网络输出相比，该层输出的特征图谱感受野较大，并包含较为丰富的语义信息，具有很强的鲁棒性，因此可有效提升本文算法的跟踪精度和鲁棒性。为了进一步增强深度特征模板的表达能力，本文利用深度特征具有丰富语义信息且对目标产旋转、缩放和平移具有不变性等优势，将输入目标图像进行旋转、翻折和高斯模糊3种方式进行处理，扩充样本数量，使深度特征模板学习到更为丰富的目标信息，样本扩充的示意图如图2所示。

图2 训练样本扩充意图Fig.2 The diagram of the training sample augmentation.

2.3 尺度估计

针对目标的尺度变化问题，本文采用文献[2,13]中的尺度估计法估算目标尺度大小，根据估测出的目标位置，利用尺度滤波器在尺度空间进行搜索，获取目标的尺度响应，进而实现准确的目标尺度估计。

2.4 算法流程图

本文算法的完整流程图如图3所示，算法首先根据初始帧给出的目标位置和大小获取用于采集训练样本的目标区域，并根据目标区域生成本文提出的二值矩阵掩膜，其次，对采集到的训练样本进行特征提取，并通过固定迭代次数的增广拉格朗日乘子法求解滤波器模板，最后将训练好的滤波器模板与测试图像进行相关操作，获取相应的目标响应，根据响应值的大小判断目标的当前位置，并通过尺度滤波器获取目标的尺度信息。

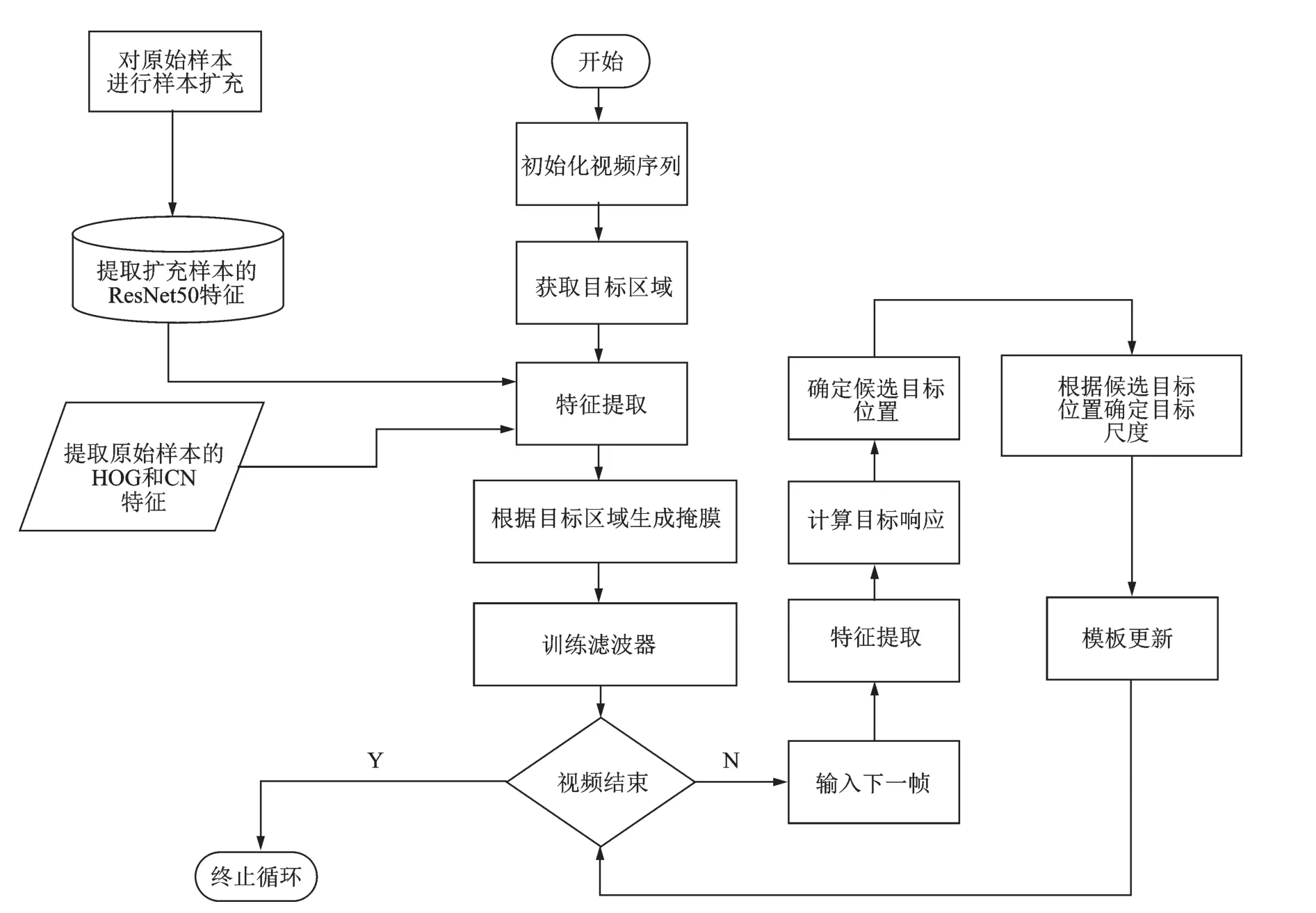
图3 算法流程图Fig.3 Flow chart of tracking algorithm

3 实验结果与分析

3.1 测试数据集和评价指标

实验测试采用的数据集为OTB-100(Object Tracking Benchmark 100,OTB100)，共包含100个视频序列，采用一次通过评估模式(One pass evaluation,OPE),评估标准采用成功率曲线面积（Area under curve,AUC）、距离精度（Distance precision,DP）评价指标。成功率曲线面积AUC计算重叠率大于某个阈值的帧数占总帧数的百分比，其结果用曲线下面积AUC表示，DP为中心误差小于20个像素的帧数占帧数总体的百分比[4]。

3.2 总体性能对比实验

本节主要在OTB测试数据集中100组具有复杂属性的视频序列上，利用OPE模式，将所提算法与5种主流算法进行对比测试，得到成功率曲线和距离精度曲线的比较结果。实验结果如图4所示。

从图4中的实验对比结果可以看出，本文采用HoG+CN特征组合的跟踪算法的平均AUC值为61.0%，比CSRDCF算法提升约3.3%，比SRDCF算法提升约1.2%，因此在不使用深度特征的情况下，本文算法仍然具有一定改进效果；本文在HoG和CN基础上加入ResNet50深度特征的算法Ours(ResNet50)在距离精度和成功率上明显优于其他算法，平均AUC值为67.6%，平均DP值为89.2%，比次佳效果算法CCOT提升大约5%，改进效果较为明显。主要原因为：（1）本文算法在二值矩阵掩膜约束的将目标搜索区域扩大为目标大小的4倍，因此训练阶段获取了数量更多的训练样本，同时由于LCM对滤波器的约束，缓解了搜索窗口扩大后的边界效应问题，不会因搜索窗口扩大导致训练样本质量降低，保证了训练样本的质量，提升了分类器的鉴别能力；（2）ResNet50深度特征在复杂背景下具有很强的鲁棒性，一定程度上提升了算法整体的跟踪精度。

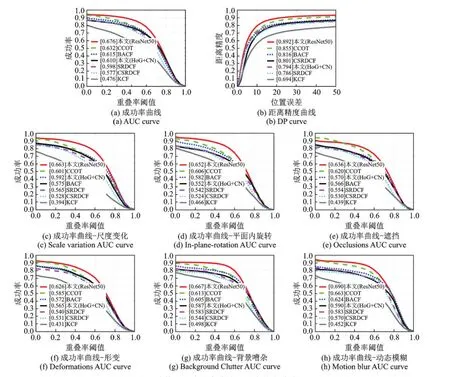
图47种跟踪算法的成功率曲线和距离精度曲线对比图Fig.4 Precision plots and success rate plots of seven trackers on OTB-100 benchmark

3.3 样本扩充对比实验

为了提升深度特征的目标模板表达能力，将输入目标图像进行旋转、翻折以及高斯模糊等处理，扩充样本数量，使深度特征模板学习到更为丰富的目标语义信息。为了说明样本扩充实验的有效性，本文在该部分实验去除了3.2节中算法使用的HoG和CN特征，仅测试单纯使用ResNet50深度特征时，进行样本扩充和不作任何处理2种方式在OTB-100测试集中针对遮挡（Occlusion,OCC）、背景杂乱（Background clutter,BC）、形变（Deformation,DEF）、运动模糊（Motion blur,MB）、平面内旋转（Inplane rotation,IPR）、尺度变化（Scale variations,SV）6种挑战下的平均AUC和DP，实验结果如表1、2所示。通过表1，2中显示的AUC和DP值可以看出，使用样本扩充方式得到的AUC和DP值总体上普遍高于不作处理的方式，该实验结果验证了对深度特征采取样本扩充可以一定程度上提升跟踪结果的精度和鲁棒性。

3.4 复杂背景条件下实验

为了充分验证本文算法效果，本文选取了包括复杂背景、目标遮挡、目标旋转、光照变化等干扰视频序列，将本文采用HoG、CN和ResNet50深度特征的跟踪算法与5种相关滤波跟踪算法进行对比测试，测试视频序列分别为MotorRolling、BikerSkiing、Skating1、Matrix以及 Lemming，其相关属性如表3所示，本文算法与5种算法在上述视频序列中的跟踪效果图如图5所示。

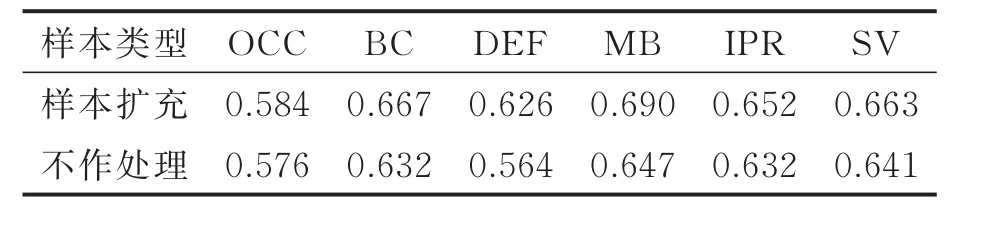
表1 样本扩充实验6种属性成功率结果Tab.1 Six attributes AUC results of training set augmentation

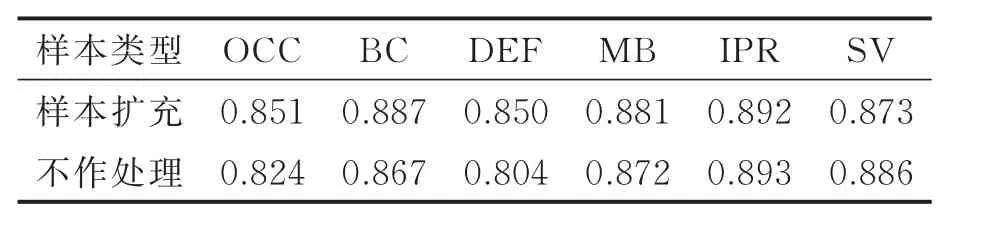
表2 样本扩充实6种属性距离精度结果Tab.2 Six attributes DP results of training set augmentation

图5(a)所示的MotoRolling视频中，目标在运动的过程中发生了旋转变化，除本文算法外其余算法均产生跟踪失败，主要原因为目标旋转时传统特征的鲁棒性较差，对旋转变化较为敏感，本文算法采用了较为鲁棒的深度特征，因此在目标运动发生变化时，依然可以保持鲁棒跟踪；图5(b)所示的Skating1视频中，当目标发生遮挡时和光照变化时，只有本文算法、CCOT以及CSRDCF可以较为准确地跟踪目标，在视频将要结束时，本文算法对目标尺度估计较为精确，效果上优于其他算法；图5(c)所示的Matrix视频中，目标的运动过程较为剧烈，背景与目标相似度极高，较为杂乱，在此环境下，只有本文算法以及SRDCF算法可以跟踪到目标，同时本文算法的跟踪准确度略微优于SRDCF；图5(d)所示的Lemming视频中，目标发生了长时间遮挡，本文算法依靠较大的目标搜索和采样区域，依然可以准确地追踪到目标；图5(e)所示的Biker视频中，跟踪的主要难点在于目标发生的平面外旋转，测试算法中除本文方法外的其余算法均发生跟踪漂移或失败，在视频结束时，只有本文算法可以较为准确地跟踪目标。综上所述，本文算法在遮挡、背景杂乱、光照变化、目标形变以及旋转等干扰下，具有较强的鲁棒性。

表3 测试视频属性Tab.3 Video sequence attributes

4 结束语

本文在相关滤波跟踪算法的基础上，提出一种基于深度特征与LCM的相关滤波算法。该方法首先利用二值矩阵作为局部掩膜消除滤波器模板边缘的能量分布，降低循环样本带来的边界效应，以此为基础扩大目标的搜索区域，进而获取更多的训练样本；在经典算法中的HoG和CN特征的基础上，加入ResNet50深度特征，利用深度特征鲁棒性较强且具有丰富语义信息等特点，通过旋转、翻折和高斯模糊3种方式对目标样本进行处理，扩充了训练样本集。与其他算法的对比实验结果表明，本文算法在跟踪精度和鲁棒性提升上具有一定的改进。算法目前存在的主要缺陷为无法满足实时性，在下一步的研究工作中可以考虑对提取得到的深度特征实现自适应降维，改善算法的实时性。