Rolle定理引出的反例

马昌秀

微分中值定理是微分学的重要理论基础，也是利用导数的局部性研究函数整体性的重要工具，是数学分析中很有实际应用价值的定理.微分中值定理是Rolle定理、Lagrange中值定理、Cauchy中值定理等基本定理的总称.［1-3］Rolle定理是微分中值定理的基石，在微分中值定理中处于十分重要的地位，是证明其他微分中值定理的关键.故掌握Rolle定理的条件、结论及Rolle定理条件的各种改变十分重要.［4-5］

1 Rolle定理

若函数f(x)满足下列条件：①在[a,b]上连续；②在(a,b)内可导；③f(a)=f()b，则在(a,b)内至少存在一点ξ，使得成立.

2 Rolle中值定理引出的反例

（1）Rolle定理中，f(a)=f()b这个条件只是充分条件，并非必要条件.Rolle定理中函数f(x)在闭区间[a,b]上连续，在开区间(a,b)内处处可导，且存在，使得成立.但在闭区间上不存在x1,x2，使得f(x1)=f(x2)成立.

本例说明，Rolle定理中，f(a)=f()b这个条件只是充分的，并非必要.

（2）Rolle定理中，函数f()x在开区间(a,b)上可导的这个条件也只是充分条件，非必要条件.函数在上连续，对内任何满足的两点c和d，子区间内至少存在一点ξ，使得.但是在内有无穷多个导数不存在的点.

例2

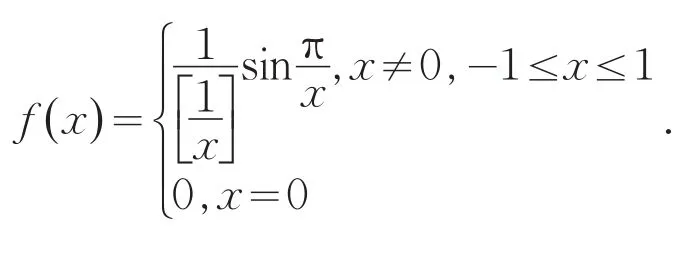
当x0=0时，f()0=0，，所以，函数f()x在上是连续的.

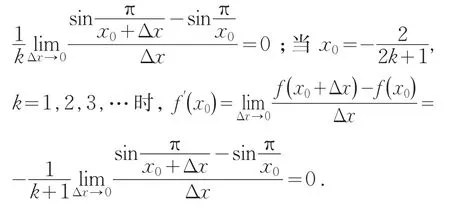
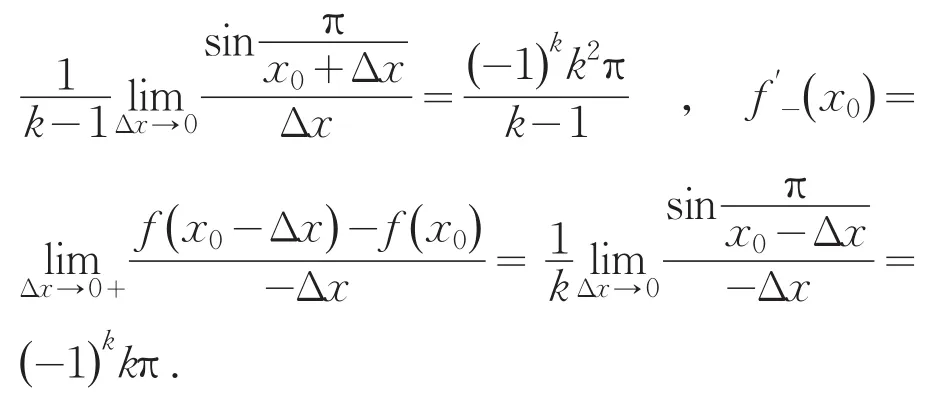
④ 若 有 -1≤x1＜x2≤1,使得f(x)1=，若记使得x1＜ξ1＜x2，有，若则当x1＞0 时 ，记使得x1＜ξ2＜x2，有.当x1＜0 时，上面的ξ2点自然在x1,x2之间，当x1,x2分布在x轴的负半轴上，可以用同样的方法证明ξ点的存在.

由此说明Rolle定理中，函数f(x)在开区间(a,b)上可导的条件是充分的，但非必要的.

（3）Rolle定理中，函数f(x)在闭区间上连续，f(a)=f(b)，f(x)在开区间(a,b)内除一点以外，处处可导，但是在(a,b)内不存在，使成立.

例3

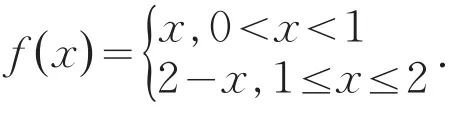
分析：函数f(x)在[0,2]上连续，f(0)==0.显然除x=1以外，它处处可导，且，所以在内不存在导数为零的点.

（4）Rolle定理中，函数f(x)在闭区间上连续，在(a,b)内可导，但在(a,b)内不存在使成立.

例4

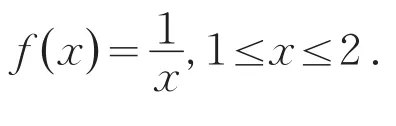
（5）Rolle定理中，函数f(x)在(a,b)上连续，在(a,b)内处处可导，f(a)=f(b)，但是不存在导数为零的点.

例5

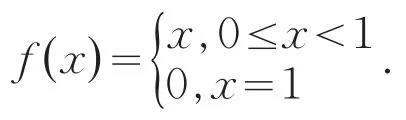
3 Rolle定理中的三个条件缺少任何一个，其结论将不一定成立

例6

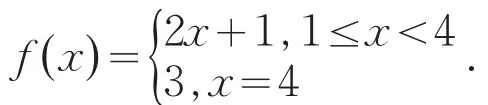
例7

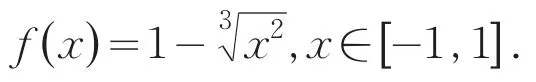
例8

4 结论

通过上述对Rolle定理的条件进行的认真分析，并对其条件和结论的各种改变情况进行的讨论，进一步说明Rolle定理中的函数f(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，且f(a)=f(b)就有成立，其条件只是充分条件并非是必要条件.只要Rolle定理的条件满足，就会有其结论成立，反之不一定成立.