压缩感知理论在空时译码中的应用
2019-10-28吴雪萍邵玉蓉姜恩华
吴雪萍,邵玉蓉,马 琳,姜恩华
随着无线通信技术的快速发展,LTE中的多入多出(Multiple Input Multiple Output,MIMO)和正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术已经日益成熟[1].OFDM技术能有效抵抗窄带干扰、提高抗频率选择性衰落的能力[2];MIMO系统则能通过借助空时码技术成倍地提高系统的信道容量,从而大大提高频谱资源利用率[3].虽然MIMO-OFDM系统有诸多优点,但在实际的工程中,仍面临着各种各样的问题[4].例如,在频谱资源受限时,如何获得较为准确的信道状态信息、提高信息传输速率是我们首要解决的问题.目前,空时译码技术已经逐渐完善,其中,空时分组码可以在不增加带宽的情况下提高数据的传输速率.越来越多的研究发现无线信道更多地表现出时域稀疏性[5-6];在信道时域稀疏的条件下,利用压缩感知理论能较好地重构出信道参数.若能将两者有机结合,将会极大地提高无线通信系统中信道估计的精度,从而降低空时译码的误码率.
1 压缩感知理论
近年来,压缩感知理论被频繁的应用到信号处理领域中,由于其良好的性能,是算法易于实现,迅速成为通信领域中极具应用前景的理论研究[7-8].就模拟信号而言,在采样频率远低于Nyquist采样频率的条件下,利用压缩感知对其采样,可以在采样的同时实现信号压缩的目的[9],在接收端,通过压缩感知重构算法重构出原来的稀疏信号.
1.1 稀疏信号
信号的稀疏是指,若信号X∈RN在某个正交基或紧框架Ψ上是可以压缩的,求其变换系数θ=ΨTX,则θ是Ψ的等价或逼近的稀疏表示.
1.2 观测矩阵
设计一个平稳的与变换矩阵Ψ不相关的M×N的观测矩阵Φ,对变换系数θ进行观测,得到观测集合如式(1)所示,其中n为噪声,
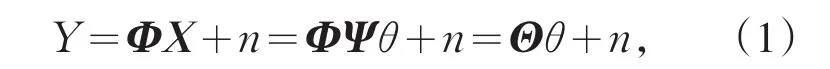
该过程也可以认为是通过矩阵Θ=ΦΨ对信号X进行观测,观测信号Y如(2)式所示.

1.3 重构算法
根据式(1)直接求解X属于欠定问题,无法正确求出方程的解.因此可转化为用l0-范数或l1-范数的优化问题求解信号X的精确或近似逼近解.利用压缩感知重构算法:贪婪算法和凸优化算法对(1)式求解,得到稀疏变换系数θ,如(3)式所示,进而通过公式X=Ψθ求得X,
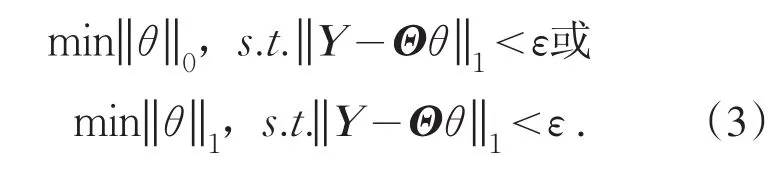
带噪声的压缩感知模型如图1所示.

图1 带有噪声的压缩感知模型
2MIMO-OFDM系统模型
MIMO技术与OFDM技术相结合,形成了MIMO-OFDM通信系统,被广泛应用于LTE-4G移动通信和WLAN网络等无线通信网络中,如图2所示.

图2MIMO-OFDM通信系统
该MIMO-OFDM通信系统的信道矩阵可以表示如(4)式所示.

式中:hNRNT表示第NR根接收天线,第NT根发送天线的信道脉冲响应.对(4)式矩阵的每个元素进行傅里叶变换,求得MIMO-OFDM通信系统的信道频域表示,如(5)式所示.
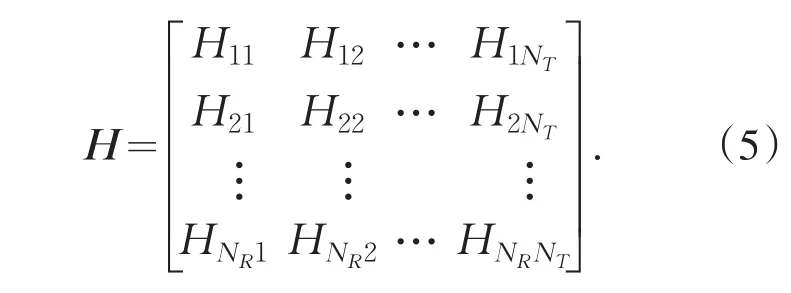
根据输入、输出以及信道参数之间的关系,MIMO-OFDM通信系统的输入和输出方程可以用(6)式表示.
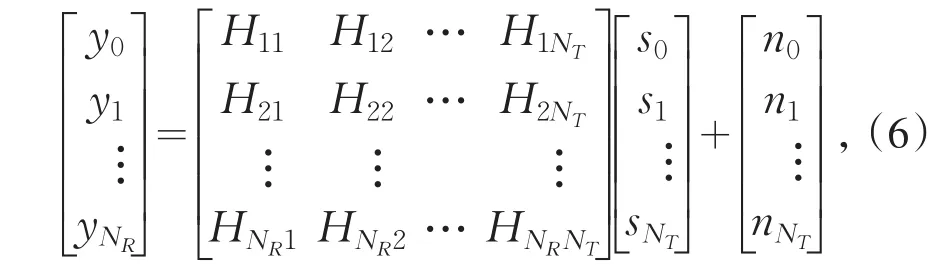
其中输入信号s和输出信号y均为频域表示,写成矢量方程如(7)式所示.
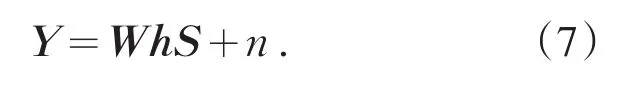
3 空时编码分析
3.1 2×1发射分集模型
采用Alamouti编码器,对两发一收的稀疏多径信道进行模拟,图3为两发一收MIMO系统中的空时编译码结构图.
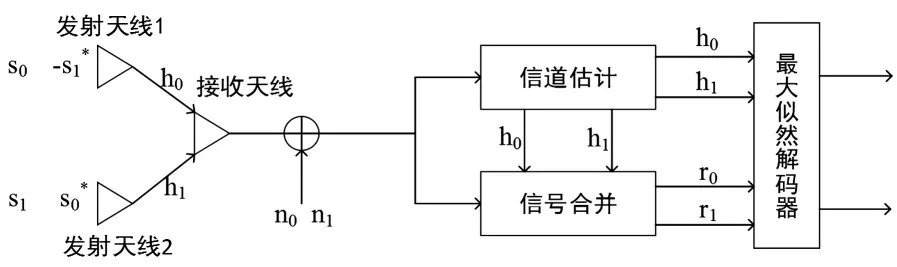
图3 两发一收MIMO系统中的空时编译码结构图
在第一个周期将S0和S1两个符号分别从天线1和天线2发射出去,下一个周期则是符号-S1*和S0*从天线1、天线2发射,其中S0*是S0的复共轭[10].假设在两个连续的符号周期内信道参数保持恒定,按照Alamouti编码规则,则输入信号矩阵如(8)式所示.
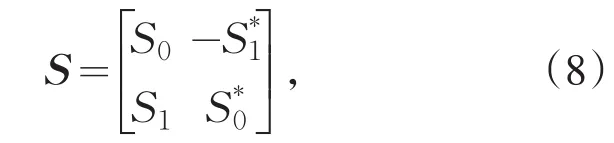
此矩阵的行数为发射端数目,列数为时刻,第一列为现在时刻,该两发一收MIMO-OFDM系统的信道矩阵的频域表示如(9)式所示,其中接收天线数目为行数,发射天线数目为列数.
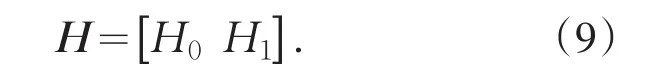
两发一收MIMO-OFDM系统的输出R的矩阵方程如式(10)所示.

把式(10)写成方程组如式(11)所示,其中r0为t时刻的接收信号,r1为t+T时刻的接收信号.

式(11)中:n0和n1分别表示在t时刻和t+T时刻上的加性随机高斯白噪声.
3.2 2×2发射分集模型
采用Alamouti编码器,对两发两收的稀疏多径信道进行模拟,若输入信号不变,两发两收MIMO系统中的空时编译码结构图如图4所示.

图4 两发两收MIMO系统中的空时编译码结构图
则信道矩阵的频域表示如(12)式.
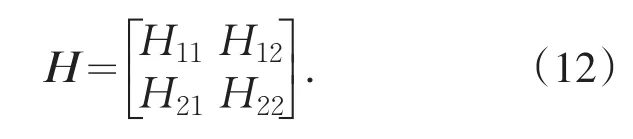
输出R如(10)式所示,其线性方程组可以用(13)式表示,其中r1和r3为t时刻的接收信号,r2和r4为t+T时刻的接收信号.
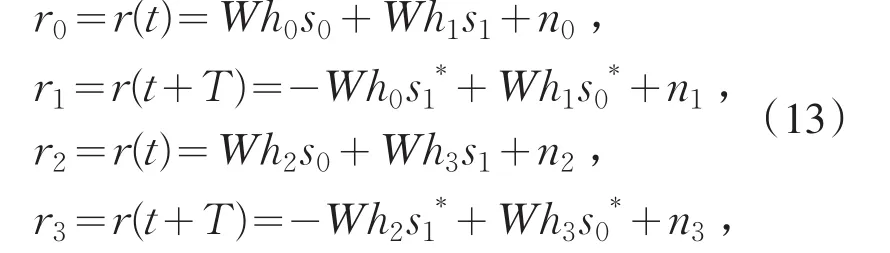
式中:n0和n2表示在t时刻的加性随机高斯白噪声,n1和n3表示在t+T时刻上的加性随机高斯白噪声.
4 基于压缩感知理论的空时译码
在接收端,需要准确估计出空时编码信息通过MIMO-OFDM系统时的信道信息,供空时译码器使用,本文采用压缩感知理论,通过设计训练序列进行信道估计.
4.1 基于训练序列的信道估计
采用训练序列估计信道信息,选择在数据发送之前插入一段已知的训练序列S0和S1,令S0=(1,1,1,…,1),S1=(0,0,0,…,0),使其通过MIMO-OFDM通信系统,其长度为信道的长度.以两发两收的发射分集模型为例,把训练序列代入(13)式,得到(14)式.

设计高斯随机矩阵phi1=randn(N1/2,N1)作为压缩感知观测矩阵Φ,对(14)式的r0、r1、r2和r3进行观测,得到观测信号y0、y1、y2和y3,如(15)式所示.
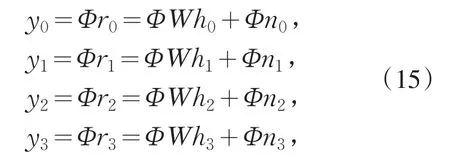
式中:Φn0、Φn1、Φn2和Φn3为噪声的观测值.根据压缩感知理论,高斯随机矩阵Φ与傅里叶变换阵W的乘积ΦW满足约束等距性RIP[11],因此,把y0、y1、y3和y3作为观测信号,ΦW作为观测矩阵,得到基于训练序列的MIMO-OFDM通信系统的信道估计的压缩感知模型如(16)式所示.
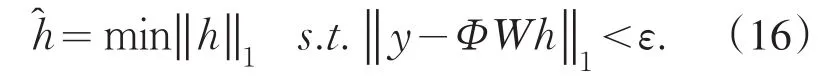
对(16)式采用重构算法 OMP、GOMP和ROMP求解,可以重构出MIMO-OFDM通信系统的信道脉冲响应h0、h1、h2和h3,供空时译码使用.同理,也可以重构出两发一收的发射分集模型的信道脉冲响应h0、h1.
4.2 信道估计的实现
根据上述理论分析,对2×1和2×2稀疏多径信道进行仿真实验,则基于压缩感知理论的OMP算法重构出的MIMO系统信道参数分别如图5和图6所示.

图5 OMP算法重构两发一收MIMO系统信道参数
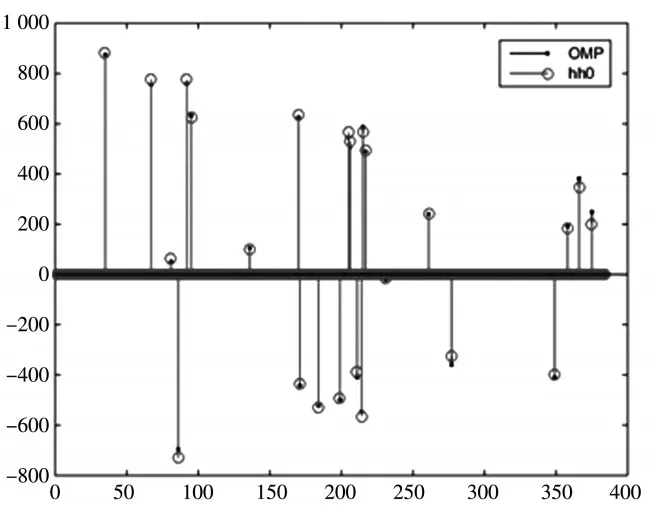
图6 OMP算法重构两发两收MIMO系统信道参数
从图5和图6中可以看出,基于压缩感知理论的OMP算法能够正确找到非零抽头的位置,并且重构信道与实际信道具有很好的拟合性.
4.3 信道估计在空时译码中的应用
利用重构出的信道脉冲响应和接收信号,对2×1的空时译码则可用式(17)表示.
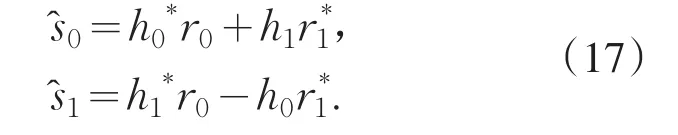
对2×2空时译码如式(18)所示.
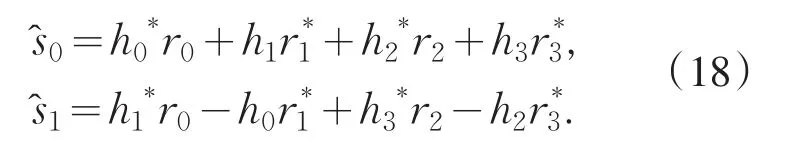
5 空时译码仿真实验
5.1 仿真实验平台搭建
在系统的发送端,信号首先经过串并转换、编码、QPSK映射、加入训练序列以及空时编码等预处理后经傅里叶逆变换(IFFT)将信号从频域变换到时域;在接收端,经傅里叶正变换(FFT)后被送入信道估计模块中估计供空时译码使用.则系统模型如图7所示.
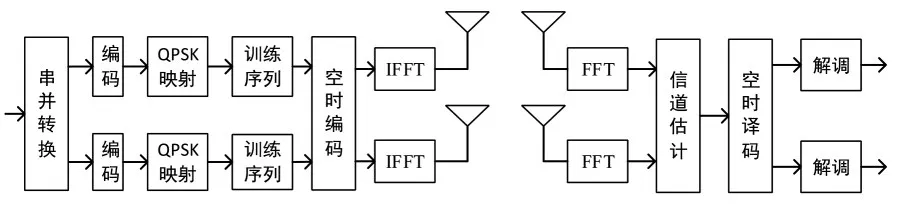
图7MIMO-OFDM通信系统仿真实验模型
5.2 仿真实验
(i)两发一收的空时译码仿真实验.为了比较LS算法、GOMP算法、OMP算法和ROMP算法在信道估计方面的性能.本文进行了如下仿真.输入信号长度N=512.对两发一收的稀疏多径信道仿真,空时译码的成功率如图8所示,误码率如图9所示.
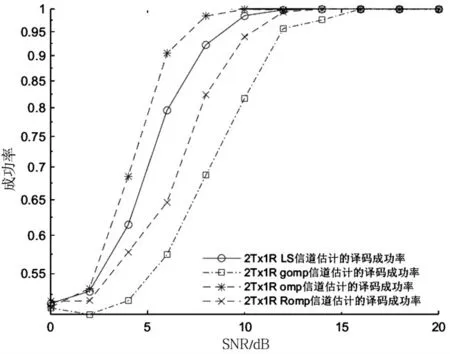
图82Tx1R的MIMO-OFDM系统空时译码的成功率

图92Tx1R的MIMO-OFDM系统空时译码的误码率
从两发一收的MIMO-OFDM系统空时译码的成功率和空时译码的误码率的仿真结果中可以得到:对于两发一收的MIMO信道模型而言,在相同信噪比的情况下,基于压缩感知重构的OMP算法估计比传统LS信道估计的性能要好,ROMP算法和GOMP算法估计则不尽理想,而GOMP算法估计性能较差.
(ii)两发两收的空时译码仿真实验.在MIMO-OFDM系统中,输入信号长度N=512时,对两发两收的稀疏多径信道仿真,空时译码的成功率如图10所示,误码率如图11所示.

图102Tx2R的MIMO-OFDM系统空时译码的成功率

图112Tx2R的MIMO-OFDM系统空时译码的误码率
从两发两收的MIMO-OFDM系统空时译码的成功率和空时译码的误码率的仿真结果中可以得到,对于两发两收的MIMO信道模型而言,对比四种算法估计,基于压缩感知的OMP算法估计较其他三种算法估计的性能要好.在相同信噪比的情况下,OMP算法能获得较优的信道估计性能,而GOMP算法的估计性能较差.
6 结论
本文研究了压缩感知理论在空时译码中的应用,针对两发一收和两发两收的MIMO-OFDM系统模型,进行了基于压缩感知重构的GOMP算法、OMP算法、ROMP算法和传统的LS算法估计,通过比较可得,无论是两发一收还是两发两收的MIMO-OFDM信道模型,利用压缩感知理论重构的OMP算法估计更为优越.本文所论述的方法能够提高信道参数的估计精确度,从而降低空时分组码STBC的译码的误码率.
