考虑成本的最大延迟时间同类机调度问题
2019-10-27刘渤海
李 凯, 杨 阳, 刘渤海
(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)
0 引言
机器调度问题一直是生产领域学者们关注的重点,单机和同型机里的多数问题已被研究,但在现实生活中,随着科技的进步,新老机器共同使用,使得所有的加工机器未必速度都相同,研究在同类机上如何更好的安排作业加工显得尤为重要。单机调度指将若干工件放在一台机器上进行排序调度。同型机调度则指的是若干速度相同的机器对工件进行排序加工。本文研究的同类机调度问题是指在若干速度不完全相同的一组机器上共同调度完成所需加工的作业。在一些经典的同类机问题的基础上,学者们不断探索在新的问题条件下,如何更好的优化结果。Zou et al.[1]考虑了作业的处理时间是其开始时间的线性递增函数的同类机调度问题,优化目标是尽量减少作业的总完工时间和以及机器的总负载,证明了该问题是多项式可解的,并给出了相关方案来解决这个问题。Kim[2]研究了同类机上调度作业具有优先约束条件来最小化加权总完工时间的问题,并提出了基于LP的列表调度启发式算法,进行了数值实验来验证。Lin et al.[3]假定完工时间有限,研究了最小化总资源消耗的同类机调度问题,提出了一种数学启发式算法,并比较结果发现明显优于PSO元启发式算法。Lee et al.[4]拓展到具有学习效应的同类机调度,其目标是寻找操作员对机器的最优分配和最小化完工时间的最佳时间表,提出了两种启发式算法,并进行计算实验以评估其性能。马英等人[5]研究了带机器准备时间的同类机最大完工时间调度问题,提出一种启发式算法,利用工件互换性质重复对最大完工时间最大和最大完工时间最小的两台机器上的工件进行交换,来提高解的质量。另外,同时考虑多个目标的同类机调度问题,也是学者们研究的方向。陈荣军和唐国春[6]考虑了以生产排序费用和发送费用总和最少为目标函数的同类机供应链排序问题,其中生产排序费用中分别用最大送货时间和平均送货时间来反映制造商服务水平,研究了两种生产排序费用情形下的目标函数,用动态规划算法构造了多项式时间近似算法,并分析了算法的性能比。

在研究相关调度问题时,完工时间问题一直被大部分学者所考虑。在实际生产中,企业在安排生产时间的同时,还必须要使生产时间不能错过客户定好的工期,以更好的满足客户需求。本文在机器成本限制的条件下,研究了作业加工的最小化最大延迟时间问题。刘乐和周泓[15]设计了含两阶段的启发式算法以及精确求解问题的分支定界算法,研究解决在一批新工件突然到达的干扰条件下,总序位干扰量受上限的单机最大延迟时间重调度问题。Lin和Jeng[16]考虑了作业在同型机上的批调度问题,目标是减少最大延迟时间和延迟作业数量,为此设计了动态规划算法来寻找两个目标的最优解,同时还设计了几种启发式算法,并进行计算实验来研究他们的相对性能。针对同类机上最小化最大延迟时间问题,Li et al.[17]为使作业最大延迟时间最小,提出了一种名为LPDT-SA的模拟退火算法,并随机生成大量数据以测试解决效果。张玉忠等人[18]揭示了分批排序问题和经典排序问题之间的联系,讨论了最小化最大完成时间以及最小化最大延迟两类问题,提出了近似算法并用“转换引理”分析了这些算法的最差性能。
本文在上述论文的基础上考虑机器具有不同固定使用成本的同类机调度问题,目标函数是总成本预算范围内最小化最大延迟时间。本文后面章节安排如下:第1节给出问题并进行分析,构建了问题模型;第2节给出设计的启发式算法;第3节对算法性能进行理论分析并给出两个算例的解答过程;第4节通过计算机软件提供随机数据进行实验验证算法的性能;第5节总结了全文并考虑了在本文基础上的进一步工作。
1 问题描述
本文研究了考虑机器固定使用成本的同类机调度问题。在给定的机器集M={Mi|i=1,2,…,m}中,有m台加工速度不同的机器,vi表示机器Mi(i=1,2,…,m)的加工速度,其中vi(vi>0)是正整数,用Si表示机器Mi(i=1,2,…,m)的固定使用成本,其中Si(Si>0)是正整数。在现实生活中,当机器的加工速度慢和使用成本高两个结果并存时,必将为生产厂家淘汰,而新式的机器加工速度快的同时,使用成本也会略高,所以我们假设当vi≥vt(i,t=1,2,…,m;i≠t)时,vi/Si≥vt/St,即加工速度越快的机器,单位成本内加工速度越快。不失一般性,将机器集中的各个机器按加工速度不增排序,使v1≥v2≥…≥vi≥…≥vm。对于任意机器Mi(i=1,2,…,m),若vi=vi+1,则令Si≤Si+1。
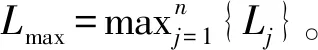
为了便于问题表示,引入下列符号。引入0-1变量xijk用于表示作业Jj是否在机器Mi的位置k上加工,若加工则为1,否则为0。0-1变量yi表示机器Mi是否被使用,若使用则为1,否则为0。整数规划模型如下:
minLmax
(1)
其中,(1)表示规划模型的目标函数;等式(2)表示每个作业只会被调度到一个机器的一个位置上;等式(3)保证对于每个机器上的每个位置只能有一个作业;不等式(4)表示第i台机器的第k个位置作业的完成时间;等式(5)表示第i台机器的第k个位置上作业的工期;等式(6)表示作业的延迟时间等于作业完工时间和作业工期之差;不等式(7)表示调度的最大延迟时间为作业的最大延迟时间;等式(8)表示确定机器是否被使用;不等式(9)表示调度总成本不能超过给定成本上限;(10)和(11)分别表示xijk和yi只能为0-1变量。
2 算法设计
本文的主要思路涉及到两方面,一方面是机器选择的问题,另一方面则考虑作业的排序问题。结合问题条件,在给定的总成本预算范围内优先选择使算法结果更优的机器,然后引申用LPT(Longest Processing Time First,最长加工时间优先)、ECT(Earliest Completion Time First,最早完工时间优先)、EDD(Earliest Due Date First,最早工期优先)规则对作业进行排序,设计一个启发式算法,实现最大延迟时间最小化的目标。
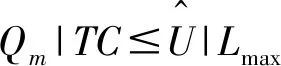
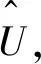
Step2将集合A中的机器重新编号:M1,M2,…,Mf。
Step3将作业按pj非增排序,若有作业pj相等,则按dj非减排序。将作业J1放在机器M1上加工,之后的作业依次遍历所有已选机器,选取完工时间Cij最小的机器Mi加工。
Step4所有作业均安排好机器加工后,将集合A中的机器上的作业,按dj非减的顺序重新排列。若有作业dj相等,则按pj非减排序。
Step5对于每一个作业j,计算Lij=Cij-dj,得到Lmax。
3 算法分析
大部分文献主要用[Lmax-Lmax(OPT)]/[Lmax(OPT)+dmax]证明算法的延迟时间的误差界,本文扩展到证明(Lmax+dmax)/[Lmax(OPT)+dmax]的误差界,并具体分析和证明了算法在机器加工速度相同和不同时的最大误差界,然后通过实际算例来说明算法的执行情况。
定理1算法H的最大延迟时间的最大误差界可以表示为式(12)。
(Lmax+dmax)/[Lmax(OPT)+dmax]
=Cmax/Cmax(OPT)+1
(12)
证明设dmax和dmin分别为作业中的最长工期和最短工期,dh为最优排序中最后完工作业的工期,Lmax(OPT)表示为问题最优排序中的最大延迟时间,Cmax表示通过该算法得出的排序中的最大完成时间,Cmax(OPT)为该问题最优排序中的最大完成时间,有
[Lmax-Lmax(OPT)]/[Lmax(OPT)+dmax]
=[Lmax-Lmax(OPT)+dmax-Lmax]/[Lmax(OPT)+dmax]
=(Lmax+dmax)/[Lmax(OPT)+dmax]-1
因为Lmax=Lij=Cij-dij,可得Lmax≤Cmax-dmin,又因为Lmax(OPT)≥Cmax(OPT)-dh≥Cmax(OPT)-dmax,可得Lmax(OPT)+dmax≥Cmax(OPT),则
(Lmax+dmax)/[Lmax(OPT)+dmax]
=[Lmax-Lmax(OPT)]/[Lmax(OPT)+dmax]+1
≤[Cmax-dmin-Lmax(OPT)]/[Lmax(OPT)+dmax]+1
=Cmax/[Lmax(OPT)+dmax]-[Lmax(OPT)+dmin]/
[Lmax(OPT)+dmax]+1
≤Cmax/Cmax(OPT)-[Lmax(OPT)+dmin]/
[Lmax(OPT)+dmax]+1
因为有Lij=Cij-dij,所以此处存在Lmax(OPT)的计算结果有可能为负数的情况,但[Lmax(OPT)+dmin]/[Lmax(OPT)+dmax]不会为负,因为易得dmin对应某一个已加工的作业j′的工期,有C′-dmin=L′,C′为j′的完工时间,L′为该作业加工的延迟时间,则有dmin=C′-L′,所以有Lmax(OPT)+dmin=Lmax(OPT)+C′-L′,又因为L′≤Lmax(OPT),所以Lmax(OPT)+dmin>0,即[Lmax(OPT)+dmin]/[Lmax(OPT)+dmax]≥0。从而,有(Lmax+dmax)/[Lmax(OPT)+dmax]≤Cmax/Cmax(OPT)+1。
定理2在机器速度相同,即同型机时,按算法H进行调度,可得式(13)。
(Lmax+dmax)/[Lmax(OPT)+dmax]≤7/3
(13)
证明在机器速度都相同的情况下,算法在Step3的步骤可以进行简化,在遍历机器选择加工时间最小的机器加工时,当机器速度相同时,即为在同型机中最小化最大完工时间问题,由《排序引论》[19]可知,当用LPT算法安排作业,令f为选择的机器数,则有
Cmax(LPT)/Cmax(OPT)≤4/3-1/(3f)
由定理1可知,
(Lmax+dmax)/[Lmax(OPT)+dmax]
=[Lmax-Lmax(OPT)]/[Lmax(OPT)+dmax]+1
≤Cmax/Cmax(OPT)+1≤7/3-1(3f)≤7/3
定理3在机器速度不完全相同,即同类机时,按算法H进行机器和作业的调度,可得式(14)。
(Lmax+dmax)/[Lmax(OPT)+dmax]≤3+2/(N-1)
(14)
证明在机器速度不完全相同时,显然,在算法中的Step3和Step4中,每台机器的最终完工时间在两个步骤中没有发生改变,即Cmax不变,由Li et al.[20]可知,Cmax/Cmax(OPT)≤2[1+1/(N-1)],由定理1可得式
(Lmax+dmax)/[Lmax(OPT)+dmax]
=[Lmax-Lmax(OPT)]/[Lmax(OPT)+dmax]+1
≤Cmax/Cmax(OPT)+1≤3+2/(N-1)
算例1设有四台机器,它们的使用成本分别为S1=6,S2=5,S3=4,S4=3,加工速度分别为v1=6,v2=4,v3=3,v4=2,有一批作业需要加工,成本总预算为13,找到最优调度方案,使得最大延迟时间最小化。参数如下:
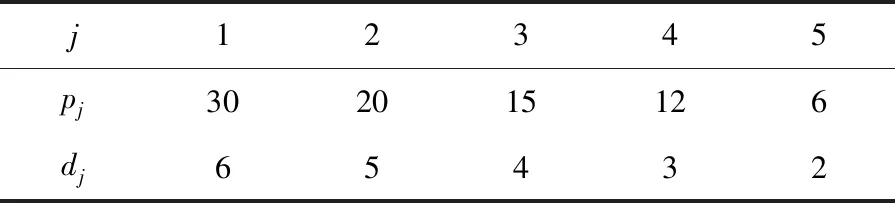
表1 作业和工期参数
解:按照算法要求选择机器,选择机器M1和M2,总成本为11,未超过预算。按照算法的调度规则将作业放在选择的两台机器上,给出算法解的甘特图。

图1 算例1的调度序列
计算可得Lmax=3,通过Lingo软件求得此问题的最优解即为本算法求得的结果,所以,(Lmax+dmax)/[Lmax(OPT)+dmax]=1。
算例2设有四台机器,它们的使用成本分别为S1=10,S2=9,S3=8,S4=7,加工速度分别为v1=5,v2=4,v3=3,v4=2,有一批作业需要加工,成本总预算为25,找到最优调度方案,使得最大延迟最小化。参数如下:

表2 作业和工期参数
解:按照算法要求选择机器,选择机器M1和M2,总成本为19,未超过预算。按照算法的调度规则将作业放在选择的两台机器上,算法解的甘特图如下:

图2 算例2的调度序列
计算可得Lmax=2.25,用Lingo得到的最优解结果选择M1、M3、M4三台机器,最优解的甘特图如下
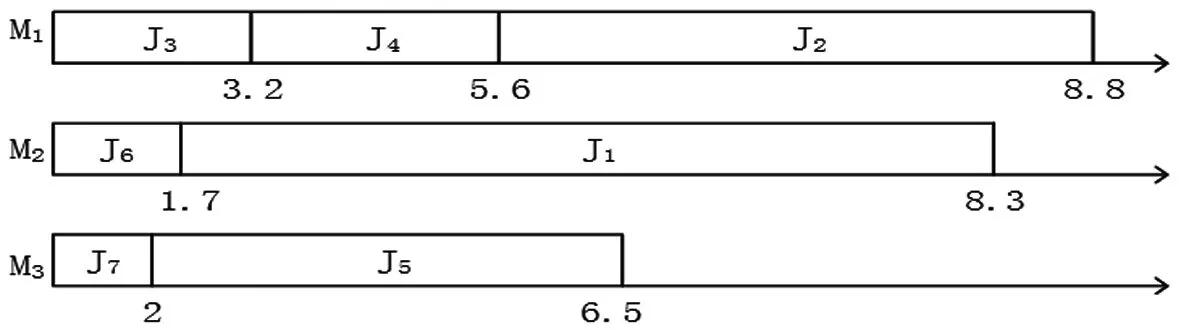
图3 算例2的调度最优序列
计算可知为Lmax(OPT)为1.8,所以(Lmax+dmax)/[Lmax(OPT)+dmax]=185/176。
4 实验数据及分析
本节将通过随机实验来验证算法的有效性。设计的算法在Java中用MyEclipse编辑器实现。实验环境:CPU:Inter(R)Core(TM)i5-3470 3.20GHz,RAM:4.00GB,线性规划模型通过Lingo软件完成。利用计算机随机生成一些数据,分别考虑作业数为20、30、40以及机器数为4、5、6时算法的效果。
表3、表4和表5分别给出λ=0.3,λ=0.5,λ=0.7时,机器数为4,5,6,作业数为20,30,40的实验结果。
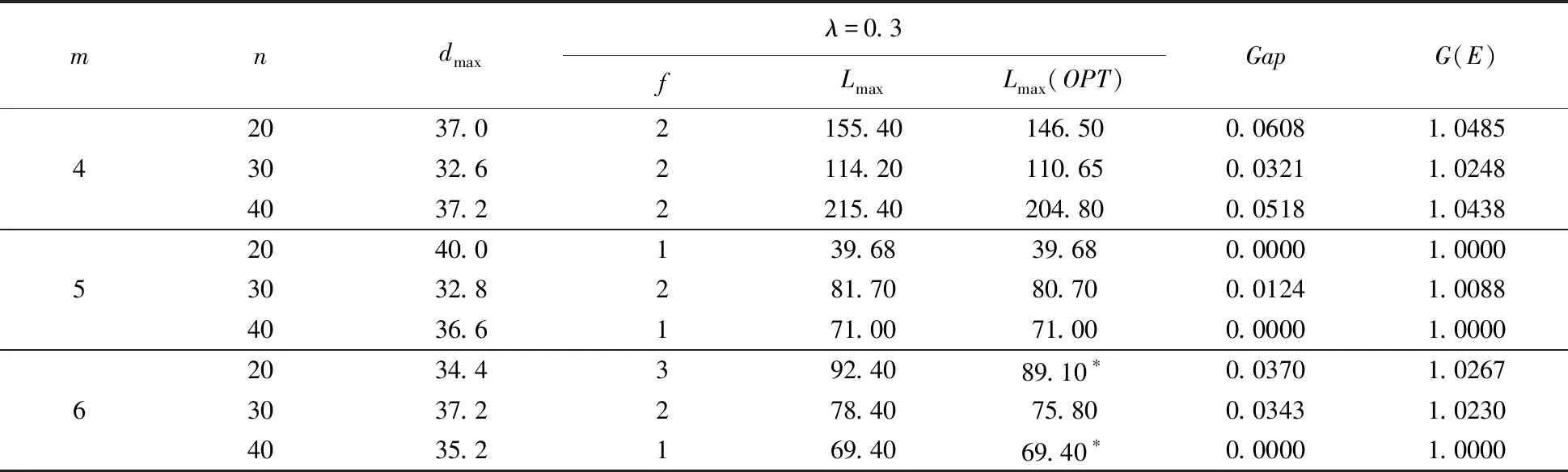
表3 λ=0.3时的实验结果
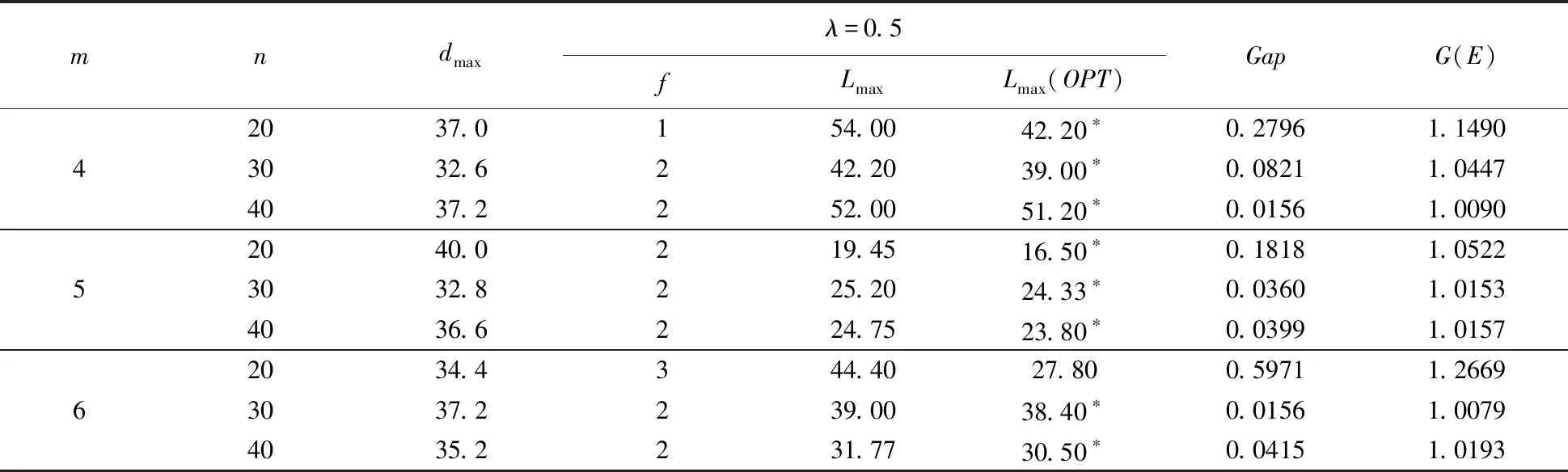
表4 λ=0.5时的实验结果
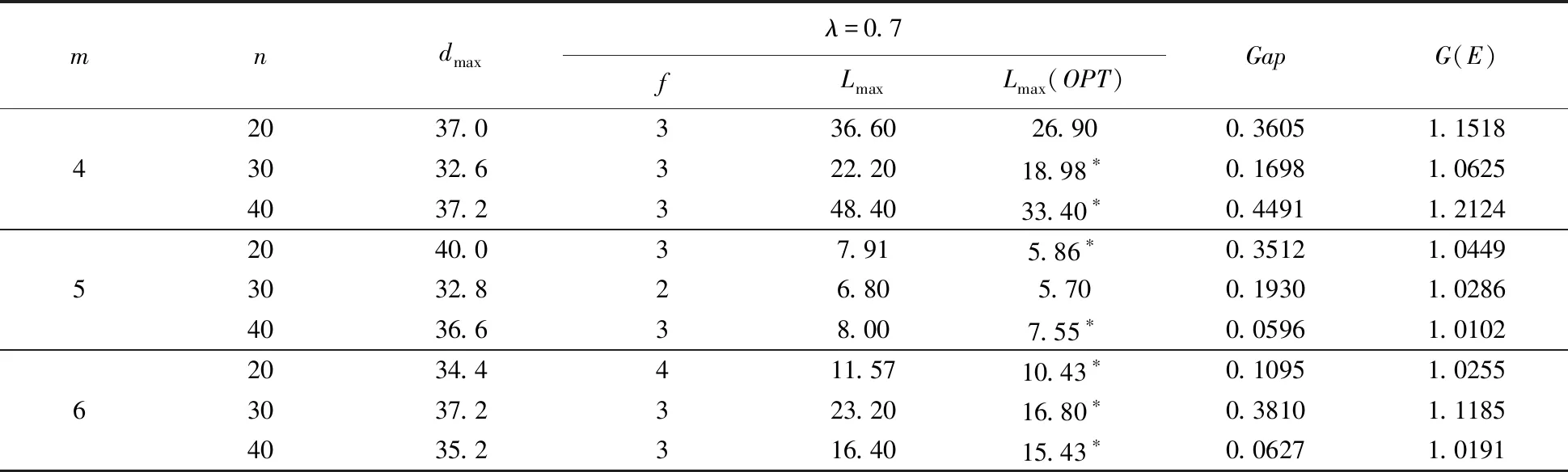
表5 λ=0.7时的实验结果
综合表3、4、5可以得出:
(1)当λ为0.3、0.5、0.7时,随着所选机器的速度变大,延迟时间相应减少 ,且G(E)的值全部都在[1,1.2669]范围内,则算法满足定理3,即(Lmax+dmax)/[Lmax(OPT)+dmax]≤3+2/(N-1),且算法的实际误差可能更小。
(2)当m,n和dmax均相同时,Lmax的值随着值的增大而减小,进一步说明了成本会对算法取得的解具有约束作用。
(3)观察实验所得的Gap值,算法获得的最好偏差是0.0000,最差误差是0.5971,平均误差为0.1353,可见算法的求解结果与最优值之间的偏离程度不大,表明算法性能较好。
5 结论
本文研究了一类考虑机器成本的同类机调度问题,目标函数是在给定的成本预算里最小化最大延迟时间。为解决该问题,我们建立了混合整数规划模型,设计了相关算法,并理论证明了(Lmax+dmax)/[Lmax(OPT)+dmax]≤3+2/(N-1),且通过大量实验检验了该算法解的有效性。
在以后的研究中,可进一步考虑机器成本与机器速度相关同类机情况下,问题的求解方法。在本文基础上,引入亚启发式算法,考虑成本与最小化最大延迟时间的多目标问题。除此之外,还可以拓展研究同类机其他目标函数的类似问题。
