基于NSGA-II的应急生产任务多目标优化模型及算法研究
2019-10-27巩玲君张纪海
巩玲君, 张纪海
(1.北京理工大学 管理与经济学院,北京 100081; 2.海南大学 管理学院,海南 海口 570228)
0 引言
近年来,我国灾害频发,给人民的生命财产带来了巨大的损失。为保障救灾的顺利进行,需要保证灾后的应急物资供应。现如今,灾后应急物资供应的手段有调用储备、应急生产、社会捐赠、应急采购、国际援助等。其中调用储备、社会捐赠、应急采购和国际援助可以看作是主要调集存量物资。所以,不少的研究重点关注了应急物资配送问题[1~7]。例如,针对多种应急资源的调度问题,汪勇等[1]构建了一个时间和成本的多目标调度模型,并设计了进化规划算法进行求解。王旭坪等[2]则从公众心理风险感知程度和应急物资未满足程度的角度,构建了混合整数规划模型,并设计了多层搜索求解算法。Zhan等[4]针对应急物流中的多供应商、多受灾点、多应急物资和多车辆的应急配送问题,提出了基于灾害情景信息更新的多目标优化模型。Alem等[7]构建了新的两阶段随机网络流量模型,并将采购、车辆、提前期以及预算分配等特征纳入模型。
学者们在应急物资配送方面的研究取得了丰硕的成果。然而,若将所有存量物资调集完毕仍不能保障受灾点的需求,决策者就需要考虑采用应急生产的方式来保障应急物资供应。例如,汶川特大地震后,为满足受灾点群众生活需求,需要紧急生产69.32万套活动板房[8]。当时采用的是援建省市对口承包建设的组织生产方式。虽然最终顺利完成了活动板房的应急生产任务,但是实施过程中也暴露出很多问题。比如有些省市不具备活动板房的生产能力或者虽然具备生产能力但是距离地震受灾点较远,为克服运距长、运费高、板材耗损等问题,所以只能采用异地生产方式,选派工作人员,去其他省市落实生产企业,这样使得协调生产变得困难,同时也很难做到资源利用的最优化。
因此,很多研究也重点关注了利用生产能力储备来解决应急生产的问题。Whybark[9]指出要考虑库存储备与应急生产能力储备的均衡,生产能力储备可以有效的降低库存水平。张自立等研究了利用生产能力储备的协议企业选择问题[10]和应急经费在政企之间的划分问题[11]。陈涛等[12]关注了协议企业生产能力储备和实物储备的协调性问题。陈业华等[13]为达到供应链协调,研究了政企共同储备应急物资生产能力的问题。罗静等[14]基于演化博弈理论探讨了政企联合实施应急物资生产能力储备的方式。张琳等[15]研究了物资企业在常规生产和加急生产情况时的政府最优支付决策和物资企业双储备决策。除了以上对应急物资生产能力储备的研究之外,Chakravarty[16]关注了不确定条件下人道救援供应链的快速响应问题,确定灾后应急物资的供应量及供应时间;Sheu等[17]通过双层递归函数,建立物资供应随机动态规划模型;Wang等[18]为解决应急物资供应短缺和采购价格高的问题,用期权契约来协调应急供应链,实现了Pareto改进。王茵等[19]从物资供应的时间和供应偏差的影响度出发,研究了多周期的应急物资供应问题。
以上对应急生产的研究可能仍无法保障灾后应急物资的供应。这主要是因为:第一,储备和协议企业生产或转产的产量总和可能无法满足重大突发事件后的物资需求;第二,激增的应急物资需求,打破了市场平衡,可能会出现原材料供不应求的情况。还是以汶川特大地震时活动板房的应急生产为例,当时短时间内需要生产1386.4万平方米活动板房,使得活动板房所需原材料彩钢板和聚苯乙烯市场供应紧张,政府不得不采取措施来保障活动板房原材料的生产和供应。鉴于以上分析,本文以应急物资需求激增的重大突发事件为研究背景,考虑必须通过应急生产才能满足需求激增的情况,重点关注原材料生产能力变化对完成应急生产任务的影响,研究应急物资的最优生产和原材料保障问题,确保应急物资高效、低廉地生产并运送到受灾点。
1 模型构建
突发事件发生后,调用应急储备是应急物资筹集的首选方式,物资紧缺时,也可以采用直接征用、市场采购、组织捐赠等筹集方法加以补充。但重大突发事件(特别是重大自然灾害)发生后,由于受灾面积大,受灾人口多,仅靠以上方式筹集到的应急物资仍然不能满足应急需求,如汶川大地震发生后,帐篷和活动板房的需求激增,需要紧急动员相关厂家进行应急生产。要想顺利完成应急生产任务,应选择应急物资生产能力强、距离受灾点较近的制造商,如果制造商的原材料储备不足,还需要为制造商选择原材料供应能力强、距离制造商较近的供应商。本文所要解决的是,在考虑上述条件的情况下,构建数学模型,给出完成任务时间最短、成本最低的应急生产方案和应急物资原材料供应方案。由于应急状况下的生产情况错综复杂,本文提出了一系列如下的假设:
(1)应急物资生产的总任务量已通过突发事件的规模、受灾人口等情况预测出;
(2)应急物资制造商(以下简称“制造商”)的生产成本已知;
(3)应急物资原材料供应商(以下简称“供应商”)的生产成本已知;
(4)各供应商向各制造商运送原材料的时间和单位运输成本已知;
(5)各制造商向受灾点运送应急物资的时间和单位运输成本已知;
(6)供应商的单位时间生产能力已知;
(7)制造商的单位时间生产能力已知;
(8)制造商生产应急物资只需要一种原材料,或者虽然需要多种原材料,但除一种原材料以外,其他原材料都很容易获得;
(9)各供应商在生产完所有原材料之后再统一向各制造商运输;
(10)各制造商没有库存,所需的原材料全部由供应商提供,并且各制造商是在所需原材料都运送到之后再开始生产。
模型的基本参数描述如下:D:需求地(受灾地);Q:应急物资的生产任务总量;Si(i=1,2,…,s):供应商;Mj(j=1,2,…,m):制造商;mcj(j=1,2,…,m):制造商Mj单位生产成本;mpcj(j=1,2,…,m):制造商Mj的单位时间生产能力;sci(i=1,2,…,s):供应商Si单位生产成本;spci(i=1,2,…,s):供应商Si单位时间生产能力;tcij(i=1,2,…,s;j=1,2,…,m):从Si到Mj的单位运输成本;tij((i=1,2,…,s;j=1,2,…,m):从Si到Mj运输时间;tcjD(j=1,2,…,m):从Mj到D的单位运输成本;tjD(j=1,2,…,m):从Mj到D的运输时间;rmj(j=1,2,…,m):Mj生产单位物资所需的原材料数量;
模型的决策变量描述如下:qij(i=1,2,…,s;j=1,2,…,m):Si向Mj提供的原材料数量;qjD(j=1,2,…,m):Mj向D提供的应急物资数量。
本文以完成应急生产任务所需的时间最短和成本最低为目标,考虑应急生产过程中的原材料保障约束,建立重大突发事件应急生产任务多目标规划模型:
(1)
(2)
模型中,公式(1)表示完成应急物资生产任务的时间最小,包括四个方面,即原材料的生产时间、原材料从供应商运送到制造商的时间、应急物资的生产时间和应急物资从制造商运送到受灾点的时间;公式(2)表示完成应急物资生产和运输任务的成本最小,也包含四个方面,即应急物资原材料的生产成本、从供应商到制造商的运输成本、制造商的生产成本以及从制造商运送到受灾点的运输成本。约束(3)表示所有供应商向第j个制造商提供的原材料数量应该等于该制造商生产应急物资所需的原材料数量;约束(4)表示所有制造商的应急物资生产数量应该等于应急生产的总任务数量;约束(5)表示决策变量的非负属性。
2 求解算法
该模型是一个针对时间和成本的多目标规划模型,直接求解非常困难。文献[20]针对后勤资源运输的特殊性,即需要考虑在运输时间最短的情况下使总运输成本最低,将涉及时间与成本的多目标规划模型转化为单目标规划模型,然后再运用单目标规划的求解方法进行求解。本文所构建的模型,针对的也是紧急状态下的应急物资供应。不过由于应急物资属性不同,对受灾点的作用也不同,因此各类应急物资需要到达受灾点的时间也各不相同,所以,我们不能单纯地考虑在时间最短的情况下总成本最小,而应该由决策者根据受灾点的情况,综合时间和成本因素做出决定。然而,对于同一个问题,由于决策者偏好不同,可能会做出不同的决策。因此,对于本文的多目标优化问题,我们重在求解Pareto最优解集,为决策者的抉择提供支撑。
2.1 算法设计
近年来,为求解多目标的优化问题,学者们运用了多种多目标进化算法[21,22],以便得到Pareto最优解集。相比以上优化算法,Srinivas和Deb于上世纪90年代提出了基于Pareto最优的非支配遗传算法(NSGA),广泛应用于多目标优化领域。但是由于其缺乏精英策略,计算复杂度比较高以及需要人为确定共享参数等缺点,Deb等又在NSGA算法的基础上进行了针对性的改进,提出了带精英策略的非支配遗传算法(NSGA-II);NSGA-II的针对性改进主要有引入了精英策略,提出了基于分级的快速非支配排序方法以及拥挤度和拥挤度比较算子,增加了采样空间,降低了算法的复杂度,而且无需再人为制定共享参数[23]。由于NSGA-II具有的众多优势,本文借助其求解模型,具体流程如见图1。
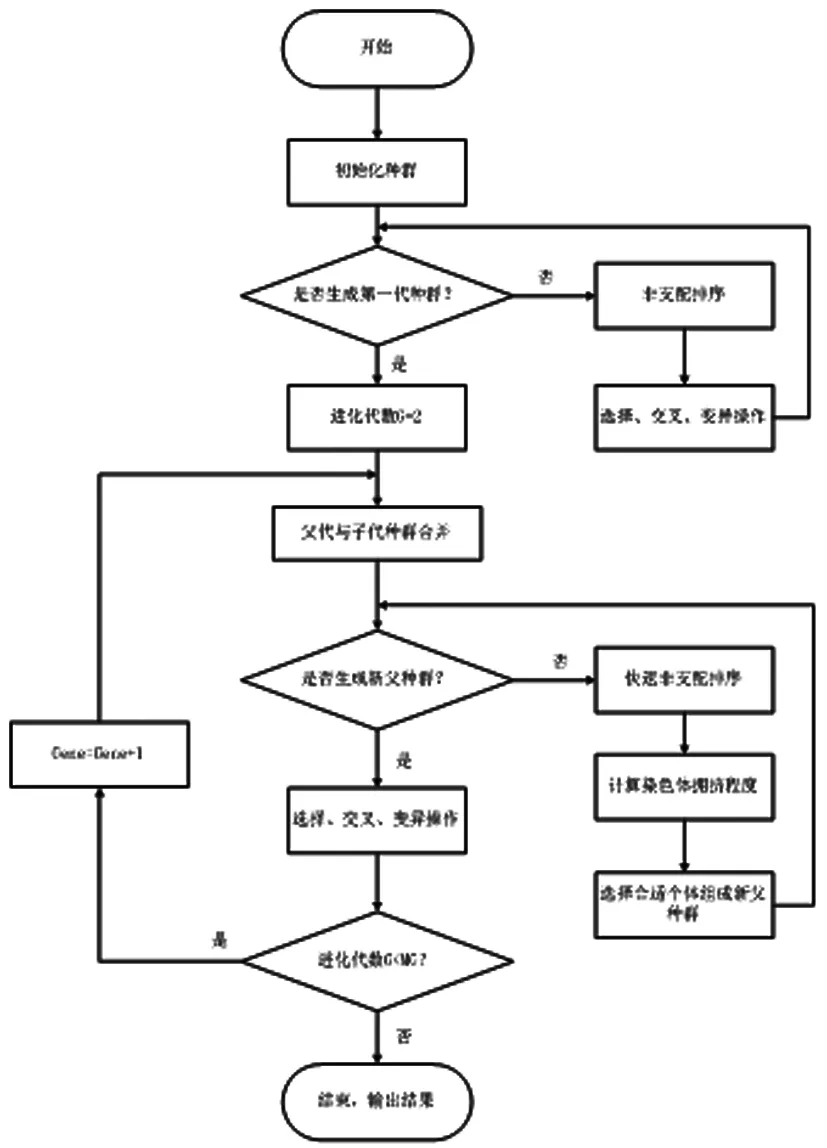
图1 NSGA-II算法流程图
步骤1参数初始化及染色体编码
假定NSGA-II的种群规模为N,交叉和变异率分别为Pc和Pm,最大迭代次数MG。
根据上述模型的特点,给决策变量编码,令两个子串组成一条染色体。其中,子串1为实数编码,长度为m,子串1表示各制造商的应急物资生产任务,即子串1中的第j个基因表示第j个制造商的应急物资生产数量;子串2为实数编码,长度为m×s,子串2代表各供应商的原材料供应情况,即子串2中的第s×(i-1)+j表示第i个供应商向第j个制造商提供的原材料数量。染色体的总长度为m×(s+1)。
步骤2种群初始化和适应度计算
参考上述编码规则,用下列方法生成初始种群,规模为N。

当子串1的初始化完成之后,再实施子串2的初始化。鉴于子串1的初始化已经完成,也即各制造商的生产任务已经确定,根据约束条件(3),也可以确定各制造商所需要的原材料数量。因此,所有供应商向各制造商提供的原材料总数为一个定值。所以,在进行子串2的初始化时,可以将子串2分为m个分串,则各分串的基因和就等于各制造商所需要的原材料数量,因此也是个定值。最后,我们再依据以上子串1的生成方式初始化各个分串。根据以上方法,最终生成初始种群。此外,需要注意的是,在处理一些实际问题时,有些原材料或者应急物资的数量是以整数的形式存在,所以在初始种群的生成时,对这写基因要随机生成整数。
在进行适应度计算之前,应该先确定适应度函数。本文中,由于目标函数都是求最小值的函数,因此,可以将目标函数作为适应度函数。基于染色体所代表的应急物资生产及原材料保障方案,根据重大突发事件应急生产任务多目标规划模型,计算每个个体的目标函数值Z1和Z2,再据此对种群中的所有染色体进行快速非支配解排序,得到Pareto前沿。
步骤3遗传操作
(1)精英选择策略
按照NSGA-II的机理,运用锦标赛方法,利用排序结果以及拥挤度的大小,对染色体进行选择操作。在选出子代种群后,将父代种群与子代种群进行合并,按照快速非支配排序和拥挤度计算,再选择出N个个体成为新一代的子代种群。
(2)交叉及变异操作
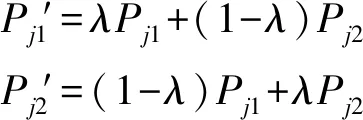
在此,还应注意,由于约束条件的存在,在交叉、变异操作结束前,还需要对约束条件的满足与否进行检验,若不满足,还需要做相关调整。
步骤4终止条件
当迭代代数达到MC时,则终止迭代,然后将结果输出。
2.2 算法复杂度分析
NSGA-II的复杂度与染色体编码的复杂程度相关,文中所用的是两参数级联编码形式:子串1的长度为m,子串2长度为m×s,则一条染色体需要占据的内存为m×(s+1)。若参数出现变化,比如供应商数量增加了u个,那么染色体长度增加到m×(s+u+1)。从需要内存的角度来比较,内存增量为o(mu),即随着参数规模的扩大,内存占用量呈线性扩张。
本文NSGA-II中,种群规模为N,迭代次数为MG,问题规模为q=m+s+1(制造商数量+供应商数量+受灾点数量)。分析NSGA-II算法的时间复杂度计算如下:初始种群生成后,每次迭代都需要适应度计算、交叉与变异操作。本文NSGA-II时间复杂度为
o(N,MG,m,s,1)=No(m(s+1))+o(Nms)+
o(N1gQ)+o(N1gQ)
≈No(m(s+1))+No(ms)
≈2No(m(s+1))
可见,NSGA-II算法的计算量与研究问题的规模的制造商数量和供应商数量成正比。
3 算例分析
情景假定:在我国某地区发生重大突发事件,对某类应急物资的需求激增,该应急物资需要一种主要的原材料,应急指挥部根据对此项应急物资的需求估计,除去已经调用的应急物资储备,还需要紧急生产和运输25000件产品。应急指挥部将此项应急生产任务下达给发展改革委,由其负责组织应急物资的生产。发展改革委根据应急物资生产潜力数据库中的数据,筛选出5个应急物资原材料供应商S1、S2、S3、S4和S5,3个应急物资制造商M1、M2和M3。它们的相关信息如下表1、表2和表3所示。据此,求出此类应急物资生产和原材料保障的最优方案,具体内容有:完成应急物资动员生产任务的最短时间和最小成本;承担应急物资动员生产任务的制造商及其具体任务数量;承担原材料供应任务的供应商及其向各制造商提供的原材料数量。
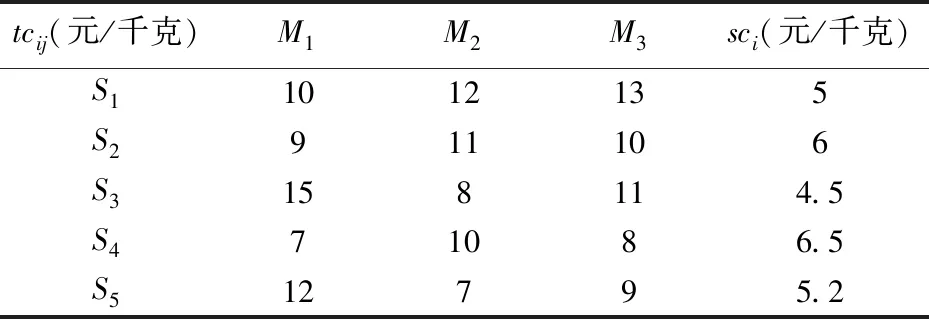
表1 供应商单位运输价格和单位生产成本表

表2 供应商运输时间和单位时间生产能力表
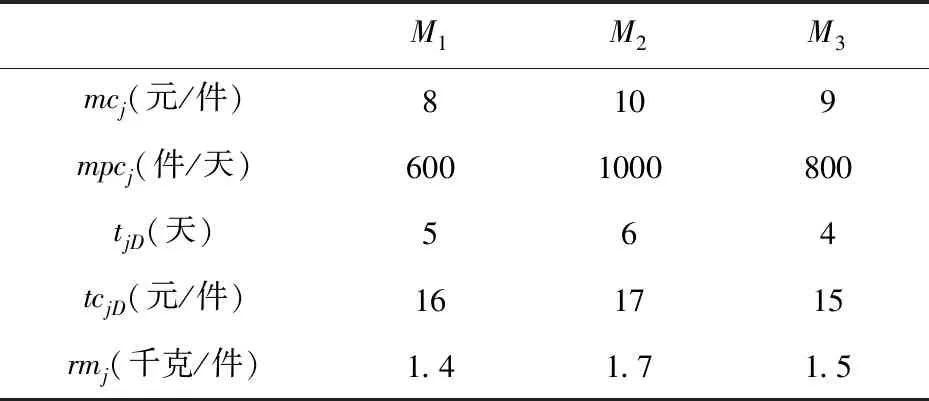
表3 应急物资制造商相关参数表
在仿真计算过程中,对算法的相关参数进行设置:初始种群规模N=200,交叉概率Pc=0.7,变异概率Pm=0.05,最大迭代次数MG=500。采用MATLAB R2015b编程实现NSGA-II,在Intel(R) Core(TM)2 Duo 3.00GHz CPU 和4GB内存的计算机上运行。根据算例所设置的数值精度,对灾后应急生产模型进行求解,运行程序得到Pareto最优解集,如图2中“常规状态下的Pareto最优前沿”所示。表4列出了Pareto最优前沿上几个具有代表性的点对应的应急物资生产模型的解,包供应商向制造商提供的原材料数量,以及制造商向受灾点提供的应急物资数量。
由图2“常规状态下的Pareto最优前沿”可以看出,该算法具有良好的收敛性,能够得到较好的Pareto前沿。从图2和表4可以看出,随着应急物资生产任务所需总时间的增加,完成生产任务的总成本也在降低。在实际的应急处置过程中,由于救援的弱经济性,政府会尽一切努力进行救援。所以,若给定某个时间阈值,在Pareto最优前沿上便可以找到优于时间的所有可行解。如图2中“常规状态下的Pareto最优前沿”所示,当给定阈值T=60时,其可行解范围是坐标轴中完成任务总时间小于60天所对应的Pareto片段。
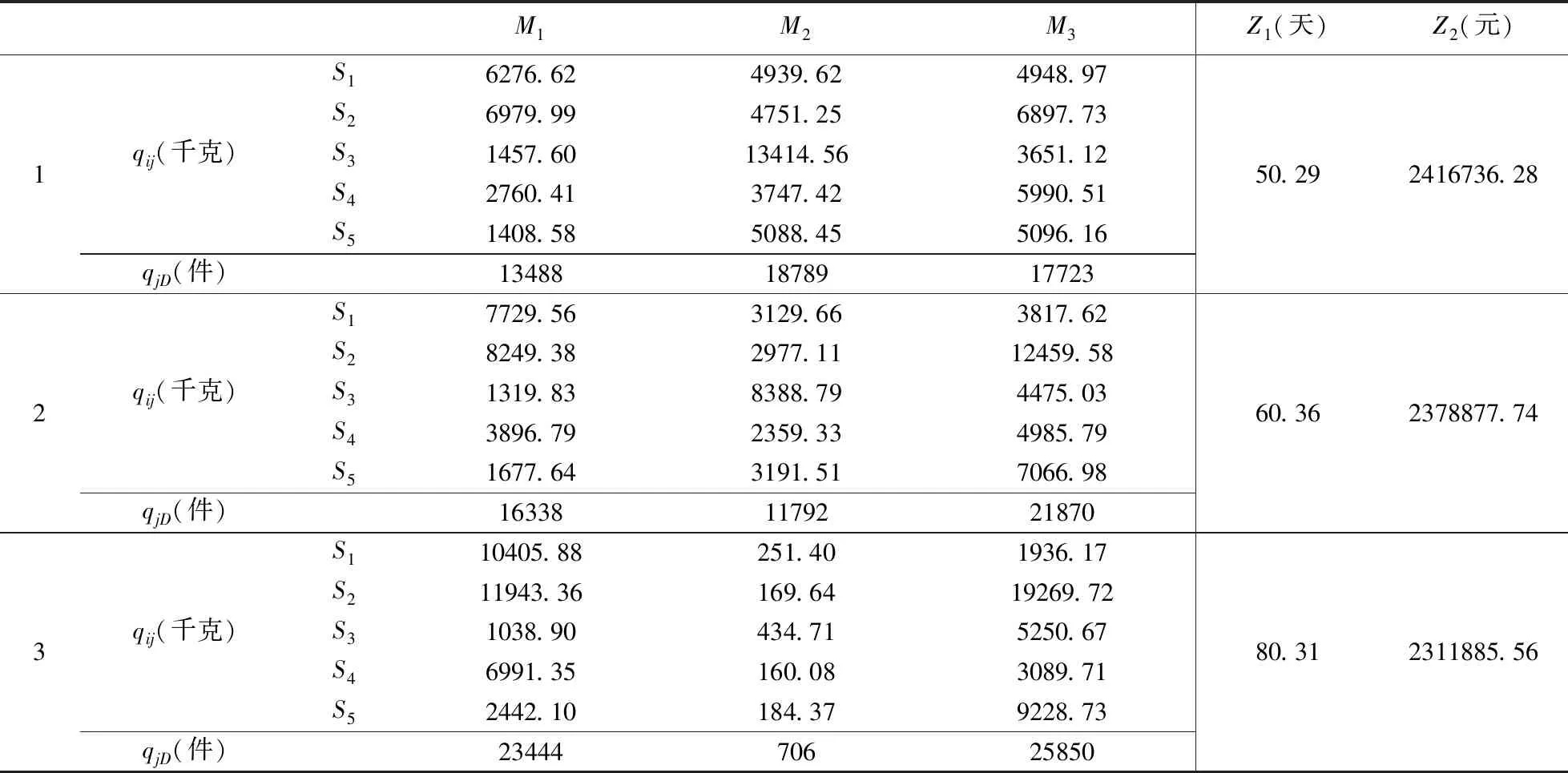
表4 Pareto最优前沿上部分点对应的解
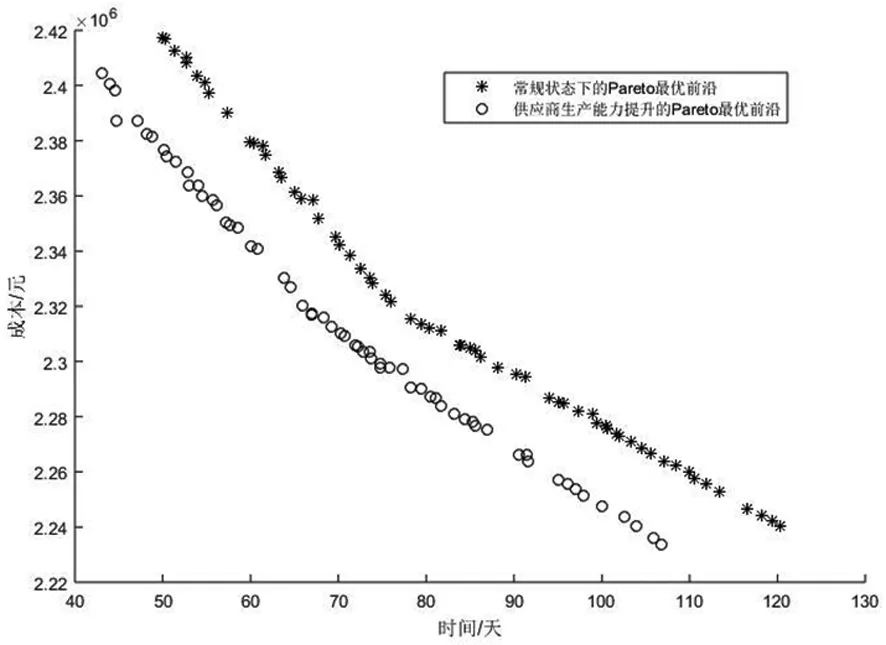
图2 两种情况下的Pareto最优前沿
本文的核心创新之处在于关注应急物资原材料生产能力变化对完成应急生产任务完成应急生产任务的影响,研究满足应急物资超常规需求的应急生产策略。因此,为了详细说明原材料生产能力变化对完成应急生产任务的影响,下面利用上述算例进行参数分析。
假设其他条件不变,各应急物资原材料供应商的单位时间生产能力提升50%,据此,求解应急物资的最优生产和原材料保障方案。同样运用NSGA-II算法,利用MATLAB编程,得出Pareto最优解集如图2中“供应商生产能力提升的Pareto最优前沿”所示。
比较图2两种状态下的Pareto最优前沿,可以看出,在“供应商生产能力提升的Pareto最优前沿”中,完成任务的最短时间可以缩短到43天,但是对于“常规状态下的Pareto最优前沿”,完成任务的最短时间为50天。由此可以看出,如果决策者将完成时间的阈值设定在50天以内,按照原有的应急物资生产和原材料供应能力,无论采取“常规状态下的Pareto最优前沿”的哪种方案都无法完成应急生产任务。所以,决策者在关注制造商的生产过程时,不能忽视应急物资原材料的生产能力变化对完成应急生产任务的影响。
此外,从算例分析还可以看出,要想在应急处置阶段真正按照模型中Pareto最优前沿的方案进行完成应急生产任务,还应该注意两个方面的问题:一方面,平时需要关注重点应急物资供应链的潜力调查和数据更新工作,特别是针对规模以上的制造商和原材料供应商,因为只有平时做好了数据调查工作,急时才可能迅速从数据库中筛选出符合要求的企业;第二,由于原材料供应商、制造商以及电力、交通等各方面的配套保障分属不同的主体控制,所以,在急时需要政府相关部门加强协调沟通,使资源能够顺畅流通,保障应急生产的顺利进行。
4 结论
重大突发事件(特别是重大灾害)发生后,受灾点对应急物资的需求激增,通过调用储备来保障受灾点需求是决策者的首选,但是当所有存量的应急物资调集完毕都难以保障受灾点供应时,决策者就需要通过应急生产来保障受灾点应急物资的供应。因此,如何快速有效地完成应急生产任务是需要解决的重要课题。基于此,本文研究了重大突发事件发生后应急生产任务多目标规划问题,关注原材料生产能力变化对应急生产任务完成的影响,以应急生产任务完成时间最短、完成成本最低为决策目标,研究了包含多个供应商、多个制造商以及单个受灾点的应急物资生产任务多目标规划模型。针对NSGA-II在求解多目标规划时的众多优势,本文运用NSGA-II进行模型求解,并在MATLAB软件中进行算例仿真。结果表明,NSGA-II可以得到较好的Pareto前沿,并且可以根据不同情况给出最优的应急物资生产和原材料保障方案。本文的研究还表明,由于应急生产与企业平时的生产活动不同,在时间紧、任务重的情况下,要想更快完成应急生产任务,需要做好原材料、资金、电力、交通等各种要素的配套保障工作。
不过,本文仅考虑了一种原材料的保障对应急物资生产能力的影响,需要注意的是,应急物资的生产可能会受到多种原材料供给的影响,还有本文只考虑了对一个受灾点的应急物资保障问题,然而,重大突发事件发生后,可能需要同时满足多个受灾点的应急物资需求,因此下一步将从以上几个方面来继续开展研究。
