基于道路堵塞及顾客时间要求的快件配送最优路径选择
2019-10-27樊相宇梁日丽武小平
樊相宇, 梁日丽, 武小平
(1.西安邮电大学 a.邮政研究院; b.现代邮政学院,陕西 西安 710061)
0 引言
现如今,网络购物已经非常普遍,要实现物品实体从供给地流向接收地,快递配送是一个必不可少的环节,不论是干线的配送还是最后一公里的配送,都会涉及到快递网络。快递网络是快递配送的基础,交通网络又是快递网络的基础,目前,由于我国道路基础设施还不够完善,在配送过程中,经常会存在中断点、拥堵点等不畅通的点[1],在确定配送路径时,需要绕过这些点,选择最优路径而不是理论上的最短路径进行配送。
对于交通网络的研究,学者们提出了最短路的关键边问题[2]和最长绕行路关键边问题[3],他们给的定义分别为在一个至少2-Edges连通的网络G(V,E)中,至少存在一条边e*,当从G(V,E)中删除e*时,使得起点s至终点t的最短路径长度增至最大,称边e为该最短路径的关键边;最长绕行路关键边是网络上最短路径上的某条边,若将其删除后,从中断点至终止点的路径长度增至最大,关键边的两种定义都没有从全局考虑,也没有结合实际问题,且是一种完全信息下的决策。另一方面,是不完全信息下的实时关键边[4]和关键路径问题[5~8],这些内容都只是单纯的研究关键边或者关键路径,没有将两者结合起来。王华[9]、李杰[10]等人将最短路径算法应用到物流配送最短路径选择中,受到前人研究的启发,文中将关键边和最优路径结合起来,针对快递“最后一公里”配送,设计了发生道路中断时,关键边及备用路径的算法。
文中首先研究了完全信息下的最长绕行路关键边问题,找到网络的关键边之后,对关键边实时监控,接着研究不完全信息下的最优路径,网络原始最短路径上其他各边的信息不完全,但关键边上的信息是完全的,当中断发生在关键边之时,车辆出发前可获得道路中断信息,可从起点处重新选择路径,避免出行者遭受最大损失。文中没有只考虑一条关键路径,借助k条最短路径[11]的思想,给出了每条边中断后对应的一组备用路径,选择运输时间小于或等于顾客可等待时间的路径为有效路径,考虑网络中各边上商场学校等场所某时人流量的情况,从有效路径中选择最优路径。
1 快件配送最优路径模型及定义
1.1 快件配送最优路径模型
文中结合实际道路网,考虑道路中断,将实际交通网络抽象为平面网络图,交叉路口为平面网络图的节点,实际路段为平面网络图的边,边上的权为实际路段的行使时间(道路正常时行驶的平均时间)[8],文中所提的最短路为时间最短,记交通网络平面图为G(V,E,C),简称交通网络,其中V={S,V1,V2,…,Vn-2,t}为节点集合,E={e1,e2,…,em}为边的集合,S表示交通网络的起始点(配送中心),t表示交通网络终止点(顾客要求送达点),m为网络中边的条数,n为节点的个数,C为边的权重。
研究的假设条件为:
(1) 假设车辆一直沿着运输方向走,不会返回,中断点之前车辆在最短路上行驶,在十字路口处等待绿灯的时间忽略不计。即文中研究有向网络,若是无向网络,可将无向图的边转换为同样边长的两条反向边。
(2)顾客可等待时间T为定值(T>hG(s,t))。
(3)车辆行驶到中断边的起始点才可获得道路是否发生中断(关键边除外)。
(4)中断只发生在最短路上,且一次只有一条边中断。
(5)一个网络图只考虑有一个人流量密集的场所(人流量密集场所用F表示)。
若关键边中断,整个配送时间最长,为了避免造成顾客不满意甚至投诉,配送企业可对关键边进行实时监控(如装置摄像头),以便随时掌握路况,降低企业损失。若关键边出现了中断,配送人员可以重新选择从起始点s到终点t的最短路径,与最短路上的其他边不同,只有到达中断边的起始点才可获得道路是否发生中断。
1.2 定义
定义1备用路径:在具有至少2边连通的网络G(V,E)中,最短路径表示为PG(s,t),最短路径上的运输时间表示为hG(s,t),设最短路径对应的任意一条边为ex(u,v)(x=1,2…k,k为最短路上边的条数),由于突发事件,边ex(u,v)发生中断,即从PG(s,t)中删除边ex,与ex边相邻的两个端点为(u,v),u点靠近起点s,v点靠近终止点t,起始点s到终止点t的所有路径称为备用路径,记为PG-ex(s,t)b,备用路径上的运输时间记为hG-ex(s,t)b,备用路径必须满足①hG-ex(s,t)b>hG(s,t),②备用路径与最短路径至少有一个点或者边不相同。
定义2关键边:从PG(s,t)中删除边ex后,最短路径记为PG-ex(s,t),最短路径上的运输时间记为hG-ex(s,t)。绕行时间记为hex:hex=hG-ex(s,t)-hG(s,t)。取各中断边对应的绕行时间最大值max{hex}对应的边e*=(u*,v*)为关键边。
定义3有效路径:若备用路径上的运输时间hG-ex(s,t)b小于或等于顾客可等待时间T,则备用路径PG-ex(s,t)b对应的配送路径称为有效路径,记作PG-ex(s,t)y。顾客可等待时间T,T(T>hG(s,t))为发生中断后顾客需要等待的总时间。
定义4最优路径:假设ex中断,有效路径为dx1,dx2,…,dxp,若①dx1,dx2,…,dxp的路段中不包含F(人流量密集场所用F表示,例如商场),则最优路径为min{tx1,tx2,…,txp}对应的配送路径,②dxp中包含F,dx1,dx2,…,dxp-1的路段不包含F,如果F所在的边eij(i=1,2,…n,j=1,2,…n)堵,则最优路径为min{tx1,tx2,…,txp-1}对应的配送路径,如果F所在的边eij不堵,则最优路径为min{tx1,tx2,…,txp}对应的配送路径,最优路径记作记为PG-ex(s,t)z。
2 算法设计
在一个边数为m,节点数为n的交通网络中,像学校、商场之类人流量密集的场所一定会在某条边上(假设人流量密集的场所F在边eij上),在某些时间段(例如节假日)对道路交通造成影响。配送车辆根据网络未发生中断时计算出来的最短路径前进,当行驶到某一节点处,网络发生中断无法通行时,最快捷的办法就是以车辆当前行驶位置为源点,终点不发生变化,仍为顾客需求点,将邻接矩阵中断边的权值用Inf表示,重新调用Dijkstra算法计算新的最短路径。
2.1 最短时间计算
网络发生中断后,对应的最短运行时间为hG-ex(s,t),起点s到点u的配送时间可以直接得到,只要得到点u到终止点t的最短配送路径及时间,即可根据李银珍和郭耀煌[12]提出的子树连接思想,得到网络中断后的最短路径及配送时间。
当最短路上边ex(u,v)中断时,u点靠近起点s,可将网络图分为两部分,如图1所示,以终点t为根的最短路径树和以u为根的最短路径子树,设M(t)是从终点可以直接到达点而不通过边ex(u,v)的点集,N(u)=V-M(t)为网络图中剩余点的集合,根据子树连通可得到如下的计算公式:
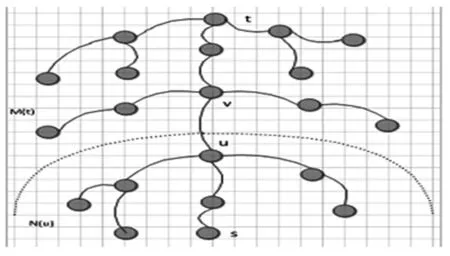
图1 最短路径示意图
hG-ex(u,t)=min{hG-ex(u,x)+w(x,y)+hG-ex(y,t)}
因为xεN(u),所以hG-ex(u,x)=hG(u,x)=hG(t,x)-hG(t,u)。因为yεM(t),所以hG-ex(y,t)=hG(y,t)。
hG-ex(u,t)=min{hG-ex(u,x)+w(x,y)+hG-ex(y,t)}=min{hG(t,x)-hG(t,u)+w(x,y)+hG(y,t)},其中xεN(u)且yεM(t)。即最短时间hG-ex(s,t)=hG(s,u)+hG-ex(u,t)。
2.2 算法设计
第一步:先根据初始网络图使用Dijkstra算法确定网络的最短路径PG(s,t)。
此时,网络没有发生中断,根据各条边的权值求出网络最短路径,令PG(s,t)=(a,b,c)。
第二步:确定网络关键边e*=(u*,v*)。
由第一步可知网络的最短路径为a-b-c,当边eab、ebc发生中断时(此时不考虑网络中存在拥堵点及顾客时间要求),应用关键边算法及最短时间公式hG-ex(s,t)=hG(s,u)+hG-ex(u,t),绕行时间公式hex=hG-ex(s,t)-hG(s,t)求出绕行时间的最大值max{hex},绕行时间最大值对应的中断边为关键边e*=(u*,v*)。
第三步:确定网络最优路径。
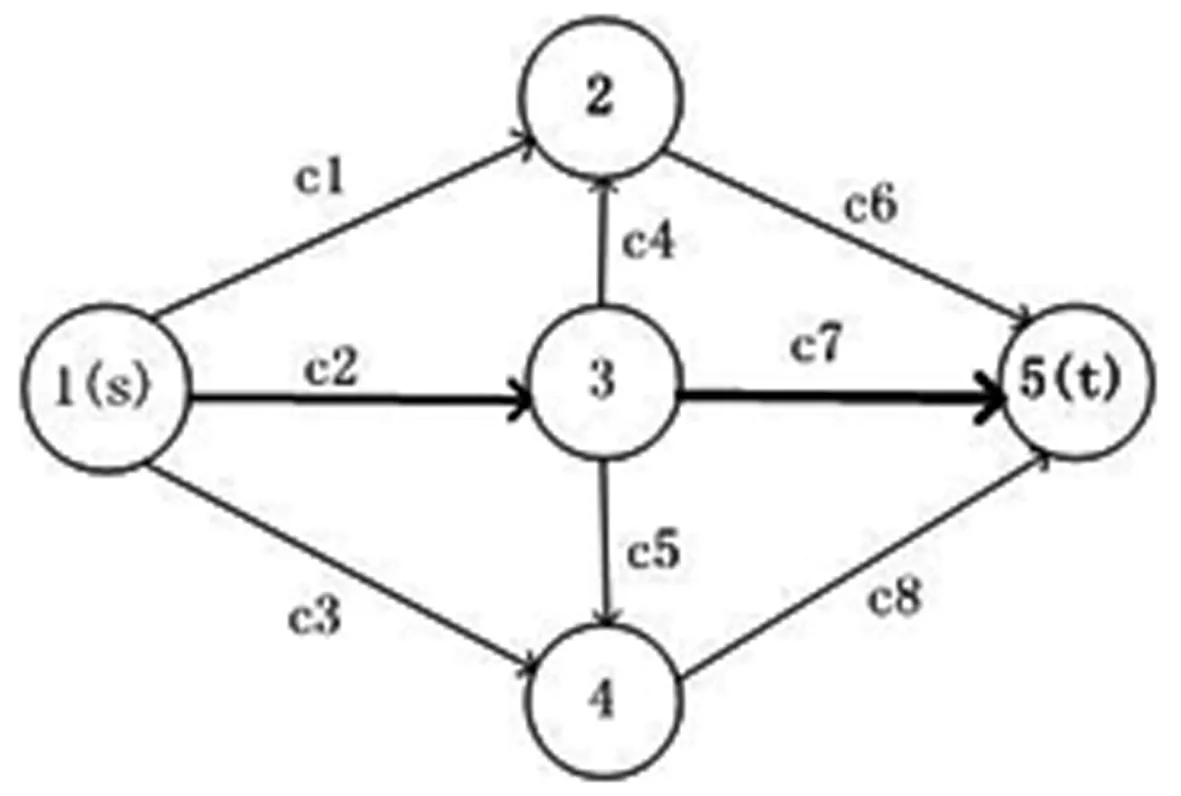
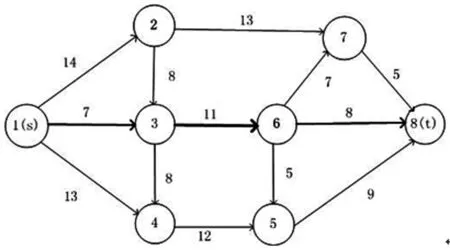
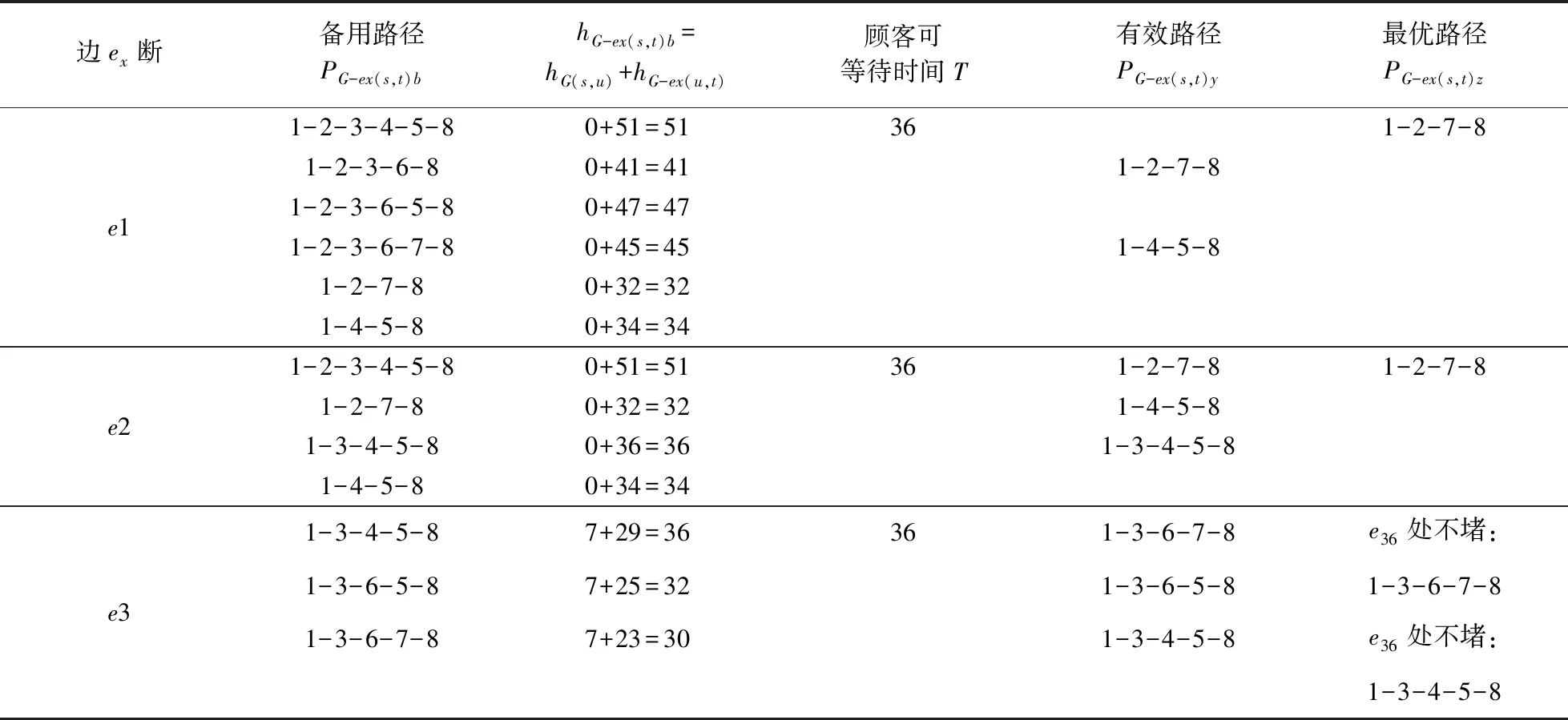
由第二步可得网络关键边为e*=(u*,v*),由于关键边上路况已知,关键边中断,应用备用路径算法求出备用路径为PG-e*(s,t)b,e1边中断,备用路径为PG-e1(u,t)b=PG-e1(s,t)b,其他边中断,备用路径为PG-ex(s,t)b=PG(s,u)+PG-ex(u,t),备用路径PG-ex(s,t)b对应的运输时间为hG-ex(s,t)b,hG-ex(s,t)b=hG(s,u)+hG-ex(u,t)若hG-ex(s,t)b 情形1F在非最短路径eij上: 第一种;e*和e1发生中断,最优路径算法(3)中的u点是起点s。 第二种;最短路上其他边ex中断,最优路径算法(3)中的u点就是中断边的起点u。 情形1结论: 备用路径时间tx1,tx2,…,txp,…,txL,假设{tx1,tx2,…,txp} 情形2F在最短路径eij上: A;F所在边及所在边之前的路段中断,最优路径求解方法及结论同情形1。 B;F所在边之后的路段中断,最优路径算法(3)中的u点是F所在边的起点i,结论同情形1。 如图2所示的配送交通网络,网络中的三角形满足两边之和大于第三边,两边之差小于第三边,Ci表示各边的运输时间,假设C1+C6 图2 配送网格 (1) 关键边 假设网络最短路径PG(s,t)=(1,3,5),则最短时间hG(s,t)=C2+C7,k=2,令e13=e1,e35=e2。 当边e13中断时,因为u=s,所以最短路PG-e1(s,t)=(1,2,5),最短时间hG-e1(s,t)=hG(s,s)+hG-e1(s,t)=C1+C6,绕行时间he1=hG-e1(s,t)-hG(s,t)=C1+C6-C2-C7。 当边e35中断时,由假设可知PG-e2(u,t)=(3,2,5),所以最短路PG-e2(s,t)=(1,3,2,5),最短时间hG-e2(s,t)=hG(s,u)+hG-e2(u,t)=C2+C4+C6,绕行时间he2=hG-e2(s,t)-hG(s,t)=C2+C4+C6-C2-C7。因为C2+C4>C1,由max{hex}可知,关键边e*=e2=(3,5)=e35。 (2)最优路径 情形1假设F在非最短路径边e12上: 当边e1中断时,网络备用路径PG-e1(s,t)b为1-2-5和1-4-5,对应的运输时间hG-e1(s,t)b为t11=C1+C6和t12=C3+C8,由假设可知,t11 当边e2中断时,网络备用路径PG-e2(s,t)b为1-3-2-5、1-3-4-5、1-2-5和1-4-5,对应的运输时间hG-e2(s,t)b为t21=C2+C4+C6、t22=C2+C5+C8、t23=C1+C6和t24=C3+C8,由假设可知,t23 情形2假设F在最短路径边e13上: 当边e1中断时,网络备用路径PG-e1(s,t)b为1-2-5和1-4-5,对应的运输时间hG-e1(s,t)b为t11=C1+C6和t12=C3+C8,由假设可知,t11 当边e2中断时,网络备用路径PG-e2(s,t)b为1-3-2-5、1-3-4-5、1-2-5和1-4-5,对应的运输时间hG-e2(s,t)b为t21=C2+C4+C6、t22=C2+C5+C8、t23=C1+C6和t24=C3+C8,由假设可知,t23 以上求解关键边及备用路径算法的思路,是对于三角不等式的应用,在求解关键边时,使用Matlab软件运行Dijkstra算法代码,逐次断开最短路上各条边,应用绕行时间计算公式,确定出关键边,没有改变Dijkstra算法本身的计算逻辑,所以关键边算法的正确性是毋庸置疑的。同理,备用路径的算法也一样。 (1)关键边算法 1)利用Dijkstra算法确定网络的最短路径PG(s,t); 2)令x=1; 3)从PG(s,t)中删除边ex,与ex边相邻的两个端点为(u,v),u点靠近起点s,v点靠近终止点t; 4)用Dijkstra算法求出新的起始点u到终止点t的最短路径PG-ex(u,t),对应的最短运行时间为hG-ex(u,t); 5)s到t的最短时间hG-ex(s,t)=hG(s,u)+hG-ex(u,t),绕行时间hex=hG-ex(s,t)-hG(s,t); 6)更新x,令x=x+1,返回到3); 7)如果x=k+1,则算法结束,取绕行时间最大值max{hex}对应的边e*=(u*,v*)为关键边。 步骤1)调用Dijkstra算法,最大计算量为O(n2);2)-6)步骤为循环计算,循环数是k,由最短路径的定义可知,k<=n-1,3)中有删除k(k (2)备用路径算法 在路段距离一定的条件下,最短路上各条边发生中断后,调整备用路径的起始点,寻找可到达终止点的所有路径。 1)调用findPath()函数知网络的最短路径为PG(s,t); 2)令x=1; 3)从PG(s,t)中删除边ex,与ex边相邻的两个端点为(u,v),u点靠近起点s,v点靠近终止点t; 4)用代码获得新的起始点u到终止点t的路径PG-ex(u,t),对应的运输时间为hG-ex(u,t),备用路径为PG-ex(s,t)b=PG(s,u)+PG-ex(u,t),备用路径PG-ex(s,t)b对应的运输时间为hG-ex(s,t)b,hG-ex(s,t)b=hG(s,u)+hG-ex(u,t); 5)若hG-ex(s,t)b 6)更新x,令x=x+1,返回到2); 7)如果x=k+1,则算法结束。 步骤1)中调用findPath()函数,最大计算量为O(n);2)-6)步骤是循环计算,循环数是k,由最短路径的定义可知,k<=n-1,3)中有删除k(k 图3为某配送中心负责的配送交通网络图,快递人员从图中的起始点s(配送中心)出发,到达目的地t点(顾客要求送达点),车辆沿着s到t的最短路径行驶,为了满足顾客的时效要求(顾客可等待时间T=36),及时给顾客配送到家,求解网络最优路径。 图3 配送网格 首先求解网络的最短路径,使用Matlab软件运行代码,求出网络的最短路径为PG(s,t)={1,3,6,8},hG(s,t)=26,所以k=3,且e1=(1,3),e2=(3,6),e3=(6,8)。然后根据关键边的求解步骤,当边ex中断时,将邻接矩阵中ex边的权值用Inf表示,即为不能通行,用Dijkstra算法求出新的起始点u到终止点t的最短路径PG-ex(u,t),对应的最短运行时间为hG-ex(u,t),s到t的最短时间hG-ex(s,t)=hG(s,u)+hG-ex(u,t)。关键边的计算结果如表1所示: 表1 关键边计算结果 当边e1中断后,将邻接矩阵中e1边的权值用Inf表示,用Matlab软件运行代码,求出网络的最短路径PG-e1(s,t)={1,2,7,8},最短时间hG-e1(s,t)=hG(s,u)+hG-e1(u,t)=0+32=32,所以绕行时间h1=hG-e1(s,t)-hG(s,t)=32-26=6,以此类推,得出绕行时间最大值为10,边e2=(3,6)为关键边,没考虑道路堵塞情况及顾客时间要求的最优路最优路径,也即理论上的最优路径为1-2-7-8、1-3-4-5-8和1-3-6-7-8。 最后求解最优路径,由于网络上一定会有学校、商场之类人流量大的场所,F可能在最短路径上,也可能在非最短路径上,根据文中的方法,求解情形1。 假设F在边e12上,由第一问可知,网络的最短路径为PG(s,t)={1,3,6,8 },hG(s,t)=26,且e1=(1,3),e2=(3,6),e3=(6,8)。当边ex中断时,将邻接矩阵中ex边的权值用Inf表示,即为不能通行,用代码获得新的起始点u到终止点t的路径PG-ex(u,t),对应的运输时间为hG-ex(u,t),则备用路径为PG-ex(s,t)b=PG(s,u)+PG-ex(u,t),备用路径PG-ex(s,t)b对应的运输时间为hG-ex(s,t)b,hG-ex(s,t)b=hG(s,u)+hG-ex(u,t),最优路径的计算结果如表2所示。边ex中断时路径PG-ex(u,t)b及运输时间hG-ex(u,t),Matlab运行结果如图4,图5,图6。 图4 边e1中断 图5 边e2中断 图6 边e3中断 表2 情形1最优路径计算结果 顾客可等待时间为36,当边e1 中断时,将邻接矩阵中边e1=(1,3)边的权值用Inf表示,使用Matlab软件运行代码,求出备用路径,备用路径中运输时间小于顾客可等待时间36的路径,即为有效路径1-2-7-8 和1-4-5-8,比如非节假日e12处不堵:1-2-7-8为最优路径,节假日e12处堵:1-4-5-8为最优路径。由于e2边为关键边,所以路况实时可知,一旦e2边中断,求出s到t的备用路径,结果与e1边中断结果相同。 由于e3边中断后,得到的有效路径不经过边e12,所以取时间最短的路径。 求解情形2,F在最短路径eij上,假设F在边e36上,根据文中方法,e1、e2中断,备用路径的计算方法同第一问,结果如图3、图4,由于有效路径不经过边e36,所以不考虑e36是否堵,直接取最短时间。由于e3在F所在边e36之后,所以备用路径为起点1(s) 到顶点3处的路径加上3处到终止点8(t),结果如图7。 图7 边e3中断 表3 情形2最优路径计算结果 表1中的最短路径即理论上的最优路径,但表2表3的结果发现考虑了道路堵塞情况及顾客时间要求的最优路径已不再是理论上的最优路径。 本文研究了在时间窗及路段堵塞约束下的最优路径,配送企业应找到某个配送网络的关键边(中断会造成最大损失),对关键边进行实时的监控,为配送人员提供一个精确的路况。综合考虑各路段堵塞及客户时间要求,找到网络中配送时间最短路径即最优路径,这样既减少了快递公司配送的成本,又保障了客户的满意度。 本文的研究没有将客户的时间窗变动考虑在内,然而在实际的配送中,同一顾客,因自己的心情、理性程度、性格、工作等情况每次可接受的额外等待时间不会是一个定值,会有一定幅度的变动。另外,最短路上发生中断,车辆绕行到其他路径上,其他路径不一定畅通,车辆的行驶时间也是一个不确定的量,因此,下一步的研究方向将是将客户的时间窗变动考虑在内的快件配送最优路径选择问题。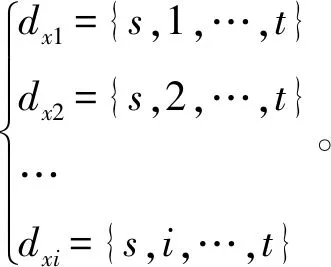
2.3 算法正确性分析
2.4 算法具体步骤及复杂性分析
3 算例分析






4 结论
