云制造平台加工能力分享调度优化研究

赵道致， 王忠帅

(天津大学 理与经济学部,天津 300072)

0 引言

近年来信息物理系统(Cyber Physical Systems, CPS)和工业物联网(Industrial Internet of Things, IIoT)技术的快速发展，催生了许多基于分享经济的资源配置模式和“制造即服务(Manufacture as a service, MaaS)”的新概念的云制造平台(Cloud Manufacturing Platform, CMP)及相应的创新业务，如“航天云网”提供的“云制造平台”和“资源共享”等服务、“淘工厂”提供的服装商家定制与工厂制造对接等服务。区别于传统车间调度情境与方法，云制造环境下企业级资源调度与配置过程中加工过程的不确定性信息准确反馈，使得云环境下加工能力分享调度方法具有动态性、实时性、柔性、反馈性等重要特征，将原来相对独立的企业车间级调度优化转化为信息兼容化，数据实时化，调度柔性化的云制造平台调度优化，将进一步影响确定条件下生产作业计划制定的准确性和制造资源利用的合理性，非云环境下的传统车间生产资源调度方法模型的解将很难达到云平台上动态实时的要求。

李伯虎院士曾于2009年率先提出了“云制造”的概念和架构体系[1,2]。之后，李伯虎等也给出了云制造的典型特征、云平台的体系架构、关键技术等方面的研究成果[3～5]。根据近年来云制造的创新实践和分享经济的理论，可给出云制造的定义：云制造就是利用IIoT技术(如GE的Predix)将企业的制造资源(asset)链接在工业互联网中，通过资源管理形成可分享利用的云制造资源，由云制造平台整合最终客户的定制化的加工与服务需求，优化配置网格化的云制造资源，完成基于知识的智能化制造过程。在云制造的体系架构和关键技术的基础上，赵道致等人基于Alvin E. Roth的匹配市场理论[6]，围绕云制造资源的匹配和调度，研究了云制造平台资源双边匹配机制及稳定性问题[7]。之后，赵道致等人又研究了面向云制造参与人有限理性决策的双边匹配机制设计[8]。

在加工能力分享的调度优化方面，随着网络化制造的发展，传统单工厂生产模式正在向网格化分布异地的多工厂转变。Ozturk等研究了定量描述不同类型多工厂生产调度计划问题及求解机制[9]。Behnamian等总结了多工厂生产调度问题的现状，得出生产制造任务调度和加工设备计划配置模型[10]。Godinho等梳理了FMS调度中应用遗传算法和粒子群优化算法的现状[11]。Tambuskar等研究了为完成静态制造任务需求，在备选设备中优选虚拟动态实体调度模型的求解技术[12]。Aalaei等研究了供应链环境下VMC的资源配置和集成调度问题[13]。Kai等研究了新工件插入的柔性车间调度问题，比较了不同的调度方法，给出了各自的应用场合[14]。Ke等研究了服装业不同情境下可持续生产能力共享机制[15]。李京生等基于面向服务的云制造思想，研究了云制造中动态资源能力服务的分布式协同调度技术[16]。王军强等基于聚类的思想给出了非瓶颈能力界定的方法，构建了云制造车间机器能力界定模型[17]。Tao等研究了智能云制造系统中基于寻优算法的仿真方法，对多个样本进行迭代计算，最后给出一种基于神经网络的寻优算法，为云制造系统确定最优序列提供了基础[18]。

上述文献从不同层面和角度对网格化调度问题进行了研究，但都没有考虑到云制造系统的客户需求的多样性、制造加工资源的分享碎片化、资源需求的时间窗约束以及供分享资源的能力约束和成本差异。现有的学者研究主要关注在理论和结构体系方面，少有利用完整的云制造技术手段，完成传统生产车间调度向云制造转型发展，建立实际云制造需求环境下企业级制造资源调度优化模型，因此，随着制造智能化和工业互联网平台的快速发展，云制造企业级资源调度将是未来新型云制造模式转型的技术前提，其理论研究意义和实际应用价值也日益明显。

本文立足于云制造平台，构建了云制造生产加工调度优化方法模型，同时，为提高企业资源利用率，考虑企业加工能力分享的时间窗，兼顾工期和成本的双重优化，设计改进的二阶粒子群算法，确定云任务的最优调度序列，并提出可分享加工能力时间窗的更新策略，最后通过算例进行仿真验证，并讨论平台如何进一步提高云资源的利用率。

1 问题描述与模型建立

1.1 加工能力分享调度问题描述

云平台在保证云资源可用能力(云资源具有的能力减现有负荷与已分配负荷)约束前提下，再根据交付时间和成本优化匹配调度云资源，以完成云任务订单的加工。云任务订单在平台上进行资源调度与配置过程中，平台根据资源提供方给出的可分享的加工能力，为云任务订单确定最优的物理资源，在实际调度中，企业有自有任务的作业计划，可看作初始调度，根据设备能力约束，将可分享的加工能力上传云平台，云平台根据云任务订单情况，将云任务作为新任务插入，新插入任务的调度则是采用尽可能在不改变初始调度方案基础上进行调度。加工能力分享的调度是以企业自有任务完成为基础，以提高企业制造资源利用率为目标，具体调度框架如图1所示。

图1 加工能力分享调度流程图

1.2 加工能力分享调度模型的构建

1.2.1 符号约定

表1 符号约定

1.2.2 模型构建

构建加工能力分享调度模型，既要满足实时制造任务前后工序的连续性和制造时间的最短，又要保证加工成本最低，因此分别以云任务的工期最短和加工任务成本最低为目标函数。由于加工能力分享调度存多个优化目标并且关联性很强，要求调度目标函数能正确反映目标函数间的关系，为此，本文采用加权平均模型对各目标函数进行归一化处理，作为调度目标，如式(1)～(3)所示。同时，根据云制造加工能力分享的实际情景对目标函数进行了约束。

目标函数:

(1)

(2)

(3)

约束条件：

Ci≤DCi

(4)

ts(i,Ni+1)≤DTi

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

式(4)为成本约束，表示完成制造任务的总成本不高于需求方对该制造任务的成本要求；式(5)为交期约束，表示制造任务最后一道工序的完工时刻不晚于需求方对该制造任务的时间要求；式(6)为资源约束，表示每个云企业同时只能加工一道工序；式(7)为工序约束，表示同一制造任务的不同工序不能同时加工；式(8)为云企业可分享加工能力约束，表示制造任务须在云企业的空闲时间窗内进行加工；式(9～12)为空闲时间窗可用约束，式(9)表示工序加工时间小于空闲时间窗，式(10)表示工序k需在空闲时间窗内能完成，式(11)表示第一道工序开工时间为可用空闲时间窗的上界，式(12)表示对其它工序开工时间约束。

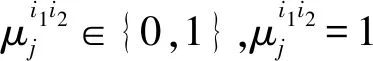
1.2.3 模型求解

模型求解的整体思路，首先，根据云企业可分享加工能力的时间窗，对模型中各制造任务i的各工序开工时间的约束进行求解；其次，根据优化目标函数，求解各个制造任务i的最优调度序列X={x1,x2,…,xn}；最后，根据调度序列，将制造任务的每道工序在云企业可分享加工能力时间窗内进行插入并进行更新，得到云任务最优的制造时间序列ts={ts(i,1),ts(i,2),…,ts(i,Ni)}。

(1)制造任务调度序列的求解

为求解各制造任务的调度序列，本文在原有二阶粒子群算法的基础上，在算法中引入制造任务的简易编码和随机权重，设计了一种改进的二阶粒子群算法(IPSO)，以提高搜索速度和获取最优解的质量。

①种群编码

利用制造任务的顺序进行整数编码，代表调度序列，长度为制造任务的个数。如粒子[3 1 5 4 2]，表示5个制造任务的调度序列为3→1→5→4→2。

②种群初始化

本算法的搜索空间假设为n维，对粒子的位置和速度的定义分别为:Xi=(xi1,xi2,…,xin),Vi=(vi1,vi2,…,vin)。初始化种群Xi、Vi的元素。

云制造加工能力分享调度优化属于组合优化问题，种群粒子的位置元素与制造任务序列一一对应。因此，对初始化种群进行变换可以利用粒子位置元素值排序法。利用粒子位置元素值建立对应的向量，按照升序对元素向量排序，此向量则代表制造任务的调度序列顺序，越小越优先调度。例如，随机生成的五维粒子位置元素向量[0.98 3.88 0.15 2.67 1.36]，由此可见在元素向量中，制造任务3的位置元素值最小，则优先调度，以此类推，得到制造任务调度序列[3 1 5 4 2]。

令优化目标函数F作为适应度函数，即：fitness(X)=F。其中：X代表制造任务调度序列顺序，fitness(X)为X的适应度值，F为按式(3)计算的优化目标函数值。

③粒子更新方法

在传统粒子群算法中，习惯将粒子飞行速度作为粒子位置的函数，这样求解结果容易造成局部最优而飞全局最优，二阶粒子群算法弥补了缺憾，而本文优化对粒子群的更新，寻求全局最优解，则在二阶算法中进一步引入随机权重ω，粒子速度更新表达式如下：

vij(t+1)=ωvij(t)+c1r1⎣pij-2xij(t)+xij(t-1)」+

c2r2⎣gbest-2xij(t)+xij(t-1)」

xij(t+1)=xij(t)+vij(t+1),∀j∈{1,2,…,n}

ω=μ+σ×N(0,1),μ=μmin+(μmax-μmin)×rand(0,1)

其中：ω为随机权重，表达了对粒子当前速度的传承，ω～N(0,1)；C1和C2代表正的学习因子，分别表示为粒子进行自我学习总结和向优秀个体学习的能力；r1,r2～rand(0,1)；pij为粒子i的过去最优值；gbest为种群的全局最优值。

采用改进的二阶粒子群算法求解加工任务加工序列的算法流程如图2所示。

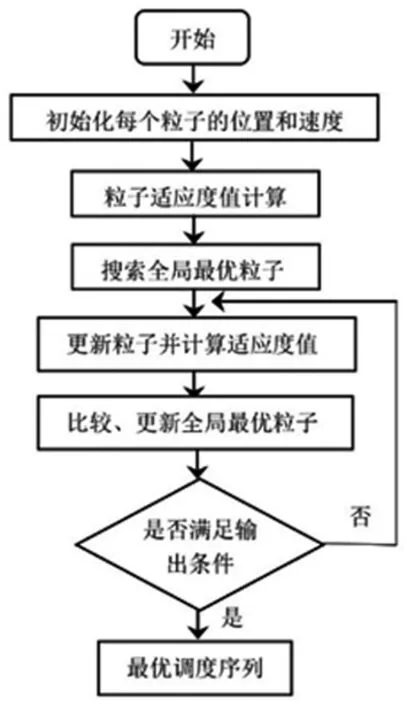
图2 算法流程图

(2)可分享加工能力时间窗的更新策略

在云制造环境下，企业可分享加工能力时间窗是随着生产计划的推进而不断变化，当云任务介入时，该云任务的每道工序要插入到各个云企业可分享加工能力时间窗内，并实时更新可分享加工能力时间窗。更新策略主要分为以下四种情况：

1)当ts(i,k)=α(j,rj),te(i,k)<β(j,rj),则更新后的可分享加工能力时间窗缩短，α(j,rj)=te(i,k-1),β(j,rj)=β(j,rj)，空闲时间窗总个数不变，如图3(a)所示。

2)若ts(i,k)>α(j,rj),te(i,k)=β(j,rj)，则更新后的可分享加工能力时间窗缩短，α(j,rj)=α(j,rj),β(j,rj)=ts(i,k)，总空闲时间窗个数不变，如图3(b)所示。

3)若ts(i,k)>α(j,rj),te(i,k)<β(j,rj)，则更新后的可分享加工能力时间窗被分为两部分，α(j,rj)=α(j,rj),β(j,rj)=ts(i,k),α(j,rj+1)=te(i,k),β(j,rj+1)=β(j,rj)，总可分享加工能力时间窗增加一个，如图3(c)所示。

4)若ts(i,k)=α(j,rj),te(i,k)=β(j,rj)，则更新后的可分享加工能力时间窗被置空，总可分享加工能力时间窗减少一个，如图3(d)所示。

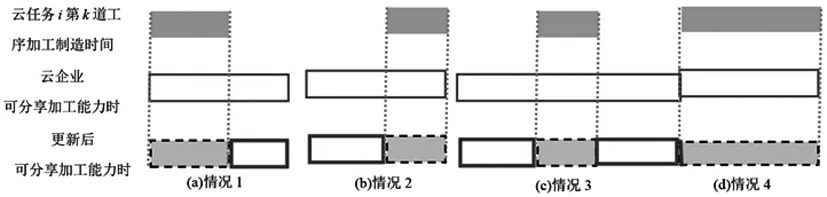
图3 可分享加工能力时间窗的更新策略图

2 算例分析

云平台在t时刻经过云任务订单整合为2 PC B2，1 SET B4，8 SET C1，3 PC C2，4SET C3，2 M C4的六个订单任务。下面根据云任务订单的加工能力要求，利用云制造加工能力分享调度模型进行调度，并对算法进行验证。根据六个制造任务相应的加工序列和所需的加工时间如表2所示，以24h为一个制造周期，给出云企业E1，E2，E3，E4，E5在初始调度后可分享加工能力的时间如表3所示。

表2 云制造任务的加工序列和时间表

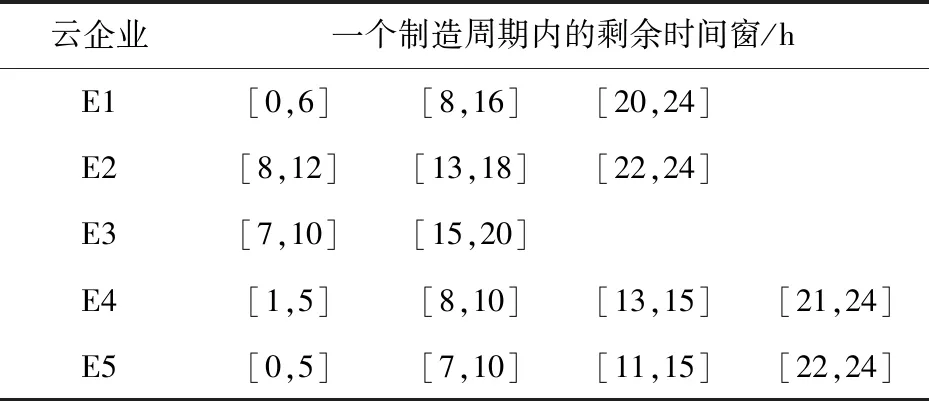
表3 云企业可分享加工能力时间表

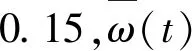
根据模型求解可得最优调度序列为[2,3,6,5,1,4]，并按照可分享加工能力时间窗的更新策略进行插入，得到图4所示云平台加工能力分享调度甘特图，其中空白代表云企业的初始调度方案，其余为可分享加工能力时间窗，完工时间为15h，成本为320万元。根据调度结果可以进一步分析云平台对于加工能力分享利用率的影响如表4所示。

图4 云平台加工能力分享调度甘特图

表4 云企业可分享加工能力及利用率分析表

图5 算法适应度变化曲线

由表可知在云平台参与后，云制造企业的能力得到充分分享，使得企业资源利用率显著提升，但对于可分享加工能力的利用率不到40%，说明云制造企业对于可分享加工能力的利用还不充分，因此可以结合云制造的特点进一步分析如何提高可分享加工能力的利用率。首先，云平台任务是按批次交付，可以在一个生产周期内对剩余资源安排多批次的云任务，直至不可再利用，进一步增加云企业经济效益；另一方面，若一个生产周期无法完成本批次所有的制造任务，可以在本周期剩余资源最小条件下，完成下个生产周期安排的部分制造任务，节省下一个周期的制造时间，进而安排更多的云任务。

为验证本文算法(IPSO)的优越性，将其分别与标准粒子群算法(PSO)、蚁群算法(ACO)、遗传算法(GA)进行比较。以相同迭代次数下，算法的收敛速度和最优解作为评价指标，设定四种算法迭代次数为150次，得到各算法适应度变化曲线，如图5所示。

以算法鲁棒性作为评价指标，四种算法分别在迭代次数为50，100，150次条件下，独立运行次数为10次，比较四种算法在三种迭代次数下运行10次得到适应度的最大值，最小值和平均值，如表5所示。

由图5可知，本文提出的算法，在提高搜索迭代速度要明显高于其他算法，获取的最优解也明显优于其它三种算法，通过表5的鲁棒性分析，表明改进的具有随机权重的二阶粒子群算法的搜索性能和平稳性相比其他算法具有优越性。

3 结论

云制造环境下的供应链主体计划调度问题具有跨地域、跨企业、多时间粒度等显著特点。本文以平台为决策主体，解决了云制造环境下生产加工能力分享调度的企业级资源调度优化问题。构建了云制造平台加工能力分享调度模型，同时设计了随机权重的二阶粒子群算法，来提高搜索最优制造序列的速度和性能，并基于云企业可分享加工能力时间窗提出更新策略，最后通过算例验证了调度机制的可行性。本文为云平台合理将网格化制造资源分享提供决策方法，协调了各主体在合作决策中的利益，实现了资源能力的高度共享。本文将进一步研究在混合周期中，云任务多批次随机到达的平台调度问题，并进一步考虑初始调度允许更改的混合调度问题。