沪深300股指期货价格发现能力研究

黄金波， 吴莉莉， 胡 蓉

(1.广东财经大学 金融学院/珠三角科技金融产业协同创新发展中心，广东 广州 510320; 2.广东金融学院 金融数学与统计学院，广东 广州 510521)

0 引言

作为国内重要的金融创新工具，我国沪深300股指期货自2010年4月16日推出以来，一直备受人们关注，业界普遍认为，股指期货的推出有助于引入做空机制，提高资本市场的定价效率。然而，沪深300股指期货推出前后的实证研究并未取得一致结论，股指期货推出之前的仿真研究表明股指期货价格发现能力有限；而股指期货推出之后，由于运行时间不长且我国资本市场仍不够成熟，股指期货是否具有价格发现功能以及程度如何都受到研究者的广泛关注，但尚没有取得一致的结论。由此可见，我国的股指期货与现货之间的价格引导关系，以及两者之间价格发现的贡献度如何，诸如此类问题都尚待深入研究。

目前国内外已有许多学者对期货与现货之间的价格发现问题进行了研究。国外期货市场的起步比较早，所以这方面的研究比较充分[1～4]。Stoll和Whaley[1]认为理性有效市场中，期货现货收益应该是完全同步的，但是他们的研究发现，即使排除非正常交易之后，S&P500和MM股指期货的收益率仍领先股票现货约五分钟、偶尔达到十分钟或更多，而滞后的股指收益对期货收益也具有温和的正向预测作用。Ghosh[2]进一步对S&P500指数及其期货之间的关系进行研究，发现二者在长期具有协整关系，在短期具有期货引导现货的关系。Tse[3,4]分别运用道琼斯工业指数和日经Nikkei225进行研究，研究结论支持股指期货在价格发现中处于主导地位的结论。Hasbrouck[5]运用多种期货合约和ETF对标普500、标普400及纳斯达克100指数进行研究，研究结果得出，不同合约的定价能力有差异，小型期货合约对标普500和纳斯达克100具有价格发现功能，标准期货和ETF都可以发现标普400的价格。Booth等[6]对德国股票市场的DAX指数进行类似研究，他们的实证结果证明，期权的价格发现功能不如期货合约。而Nam等[7]基于韩国股指的数据则得出股指期权和期货都具有价格发现的功能。Brooks等[8]、Zhong等[9]以及Douligeris和Serpanos[10]分别对英国、墨西哥和希腊的股票指数进行了研究，研究结果显示，在样本期内这三个国家的股指期货合约都具有价格发现功能。

虽然我国股指期货起步较晚，但国内已有许多学者运用各种计量方法对沪深300股指期货与指数现货之间的价格发现问题进行了研究，并得出了不同甚至相反的结论[11]。严敏等[12]、Yang等[13]以及蒋勇等[14]的研究认为我国现货市场在价格发现过程中占主导地位，股指期货的价格发现能力有限；而华仁海和刘庆富[15]、任远[16]、何诚颖等[17]以及刘向丽和张雨萌[18]得到相反的结论，他们认为期货市场在信息传递过程中占主导地位，具有价格发现功能。也有部分学者得出期货与现货之间存在相互引导关系，例如方匡南和蔡振忠[19]及左浩苗等[20]的研究发现我国股指的现货市场与期货市场存在双向因果关系。张腾文等[21]则首次区分了价格变化的趋势，并且实证研究得出在上涨趋势中期货具备价格发现功能，股指期货领先于现货；而在下跌趋势中，股指期货与现货互为Granger因果关系，股指期货与现货存在相互引导的关系。

综上可知，国外学者基于发达市场数据研究所得的结论较为一致，而国内学者的研究结论分歧较大，因此我国的沪深300股指期货价格的发现功能如何还有待进一步地探究。我们认为国内学者研究结论的分歧并不存在对错之分，究其根源在于研究对象、样本选择和研究方法的不同。在研究对象方面，部分学者利用沪深300期货和现货的收益率数据进行研究，而另一部分学者则利用收盘价或对数价格来研究，从而得出不同的结论是可以理解的。在样本选择方面，一些学者利用仿真数据进行研究，而另一些学者运用实际数据进行研究；一些学者选择上涨趋势中的数据，另一些学者选择下跌趋势中的数据，更多的学者则不做任何趋势分析和判断，导致不同的样本选择得出不同的研究结论。最后在研究方法上，研究期货价格发现能力的研究方法众多，各种研究方法没有绝对的对错之分，也缺少统一的选择标准，这也是导致研究结论不一致的重要原因。

基于以上几点，本文在以下两个方面对现有研究进行拓展：第一，本文对研究对象进行了区分，分别运用收益率数据和价格数据进行研究。一般而言，价格数据是非平稳的，需要用协整分析，而收益率是平稳的，可以用向量自回归模型进行分析。第二，本文区分了上涨趋势和下跌趋势，研究不同趋势下期货价格发现能力的差异，从而得出期货价格发现能力的非对称性。因此，本文以下内容首先把沪深300股指及其期货数据序列分为上涨与下跌两个阶段，分别对价格数据和收益率数据进行描述性统计分析和平稳性检验。然后对平稳的收益率数据建立向量自回归模型，在此基础上进行Granger因果检验，验证两者之间是否具有相互引导的作用；接着利用脉冲响应函数和Hasbrouck方差分解分析期货市场与现货市场两者谁在价格发现功能中占主导地位。针对不具有平稳性的期货价格与现货价格数据，本文采用Johansen协整检验分析它们之间是否具有长期稳定的均衡关系，再利用向量误差修正模型分析二者的短期价格行为。

1 数据与描述性统计

1.1 数据

本文采用沪深300指数及其期货当月主力合约的5分钟高频数据作为研究对象。之所以选取5分钟高频数据，是因为相关研究发现数据抽取的频率越高，市场微观结构噪声越明显[22]；同时为了保证充足的样本量和估计的准确性，数据抽取频率又不宜过低，5分钟高频数据是权衡二者后的最优结果。仿照张滕文等[21]的方法，本文将相对于前期最低点涨幅超过30%的走势定义为上涨趋势，将相对于前期最高点跌幅超过30%的走势定义为下跌趋势(阶段详细划分见表1)。由于沪深300股指期货交易时间为9:15～11:30和13:00～15:15，而沪深股票市场交易时间为9:30～11:30和13:00～15:00，为便于数据处理，需要剔除交易时间不重叠的数据。另外股市开盘前5分钟的数据噪音比较大，因此我们选取的交易时间为9:35～11:30和13:00～15:00。本文使用的数据来自Wind咨询经济金融数据库。

表1 样本区间划分

1.2 描述性统计

原始数据序列为沪深300指数与沪深300股指期货收盘价，为了减少数据序列的异方差问题，我们对其进行对数处理，取对数后的现货和期货价格序列分别记为S和F，同时记沪深300指数与沪深300股指期货的对数收益率为s和f。表2给出了S和F及s和f的描述性统计，从中可以看出，上涨阶段和下跌阶段具有非常不同的数据特征。从偏度系数来看，S和F的分布在上涨阶段存在左偏(偏度系数小于零)且左偏程度小于下跌阶段，s和f的分布在上涨阶段存在右偏(偏度系数大于零)，而在下跌阶段存在左偏(偏度系数小于零)。从峰度系数来看，四个序列的分布在上涨阶段的峰度系数小于下跌阶段。S和F在上涨阶段的峰度系数小于3，而在下跌阶段大于3，说明上涨阶段S和F的分布不存在“尖峰厚尾”现象，而在下跌阶段具有“尖峰厚尾”现象。无论在上涨阶段还是下跌阶段，s和f的峰度均都大于3，说明s和f的分布具有“尖峰厚尾”现象。JB统计量在1%的显著性水平上拒绝各个序列服从正态分布的假设。

表2 沪深300指数与沪深300股指期货价格及收益率描述性统计

2 沪深300指数期货价格发现能力的实证检验

2.1 ADF检验

因为研究中考虑到变量可能存在的非平稳性，避免模型中出现的伪回归问题，所以在利用时间序列变量进行分析之前，我们首先分别对上涨阶段与下跌阶段的两个价格序列的平稳性进行扩展迪基——富勒检验(ADF)。ADF检验的具体方法是估计回归方程:

Δy1=yt-yt-1

(1)

式中，yt为原始时间序列；t为时间趋势项；yt-1为滞后1期的原始时间序列；Δyt为一阶差分时间序列；Δyt-j为滞后j期的一阶差分时间序列；α为常数；δ、γ、λj为回归系数；p为滞后阶数；ut为扰动项。

检验结果如表3，无论在上涨阶段还是下跌阶段，在5%的显著水平下不能拒绝S和F序列存在单位根的假设，说明S和F时非平稳的时间序列。而在5%的显著水平下能够拒绝s和f存在单位根的原假设，即s和f是平稳的。从而可知S和F都是一阶单整序列。

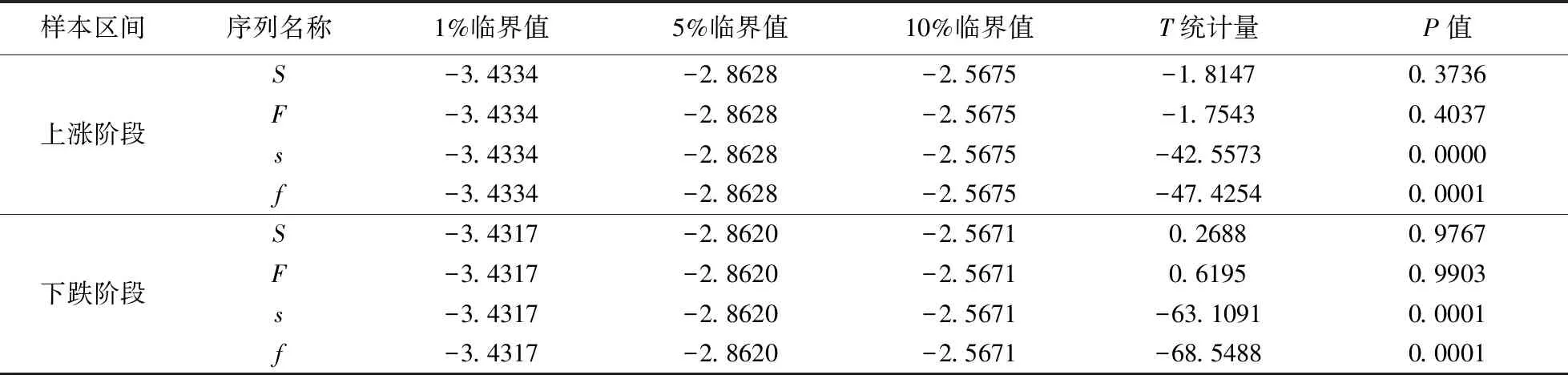
表3 沪深300现货价格与期货价格的ADF检验结果

2.2 VAR模型的估计

由于收益率数据是平稳的时间序列，因此可以直接利用向量自回归模型(VAR)考察期货现货收益率之间的动态变化规律，在进行VAR模型回归之前需要确定最优滞后阶数，各种选择标准所得的最优滞后阶数如表4。由表4可知，在上涨阶段，LR、FPE、AIC和HQ四个检验标准都选择4阶为最优滞后阶数，所以上涨阶段的VAR模型最优滞后阶数选择4。在下跌阶段，五个标准中，3个标准都选择滞后阶数为7，所以下跌阶段VAR模型最优滞后阶数选择7。

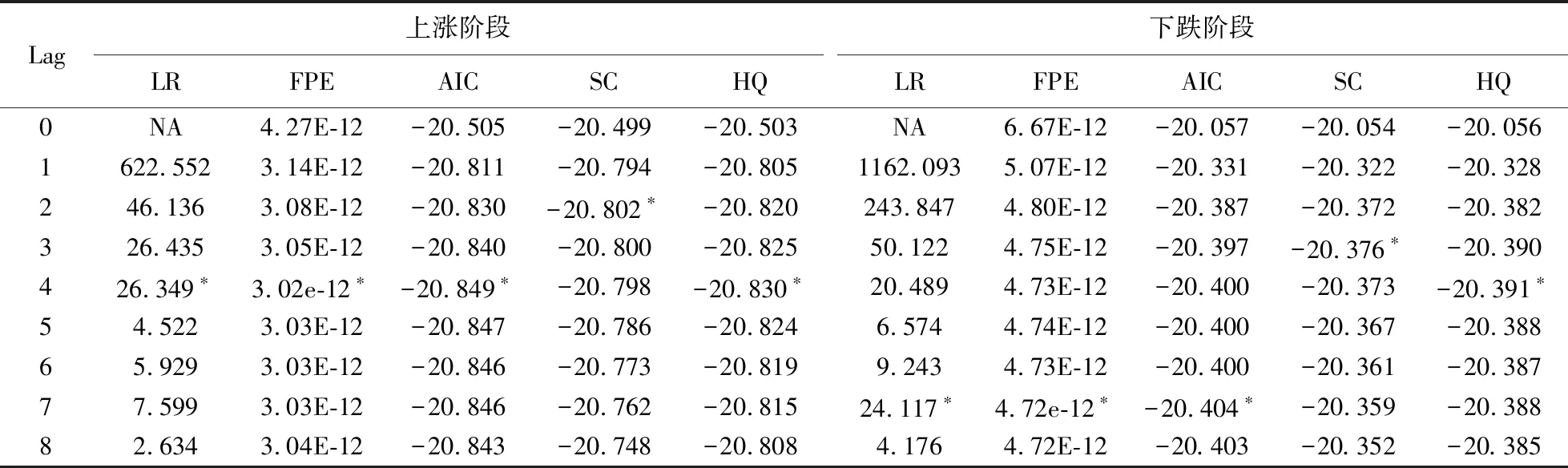
表4 最佳滞后期选择检验

上涨阶段的VAR回归方程如下:

f1=-0.0185ft-1+0.0276ft-2+0.06303ft-3-0.0348ft-4-0.0472st-1-0.0219st-2-0.0291st-3+0.0274st-4+0.0001

(-0.4712) (0.6057) (1.3206) (-0.8498) (-1.1092) (-0.4839) (-0.6488) (0.7190) (3.2955)

st=0.5418ft-1+0.2272ft-2+0.1953ft-3+0.0801ft-4-0.4193st-1-0.1821st-2-0.1647st-3-0.0694st-4+0.0001

(15.0384) (5.4244) (4.6503) (2.1290) (-10.7079) (-4.3804) (-3.9883) (-1.9812) (2.9070)

注：圆括号数据为对应的t值，下同。

从回归结果来看，在上涨阶段，期货和现货收益率的滞后项对当期的期货收益率都没有显著的影响，说明现货收益率对期货收益率没有引导作用；而期货收益率的滞后项对当期的现货收益率有非常显著且正的影响，现货收益率的滞后项对当期现货收益率有显著且负的影响，说明期货收益率对现货收益率具有引导作用。

下跌阶段的VAR回归方程如下：

ft=-0.0759ft-1-0.0222ft-2-0.0644ft-3-0.0740ft-4-0.0369ft-5-0.0653ft-6-0.0637ft-7

(-2.5268) (-0.6255) (-1.7478) (-1.9904) (-0.9920) (-1.7975) (-2.0281)

+0.0298st-1+0.0620st-2+0.0968st-3+0.0281st-4+0.0423st-5+0.0742st-6+0.0923st-7-0.0001

(0.8684) (1.6318) (2.4884) (0.7182) (1.0816) (1.9650) (2.9159) (-1.8166)

st=0.4985ft-1+0.2658ft-2+0.0890ft-3+0.0271ft-4+0.0370ft-5+0.0133ft-6+0.0069ft-7

(18.9191) (8.5243) (2.7542) (0.8321) (1.1347) (0.4165) (0.2513)

-0.4579st-1-0.1917st-2-0.0416st-3-0.0583st-4-0.0391st-5-0.0192st-6+0.0229st-7-0.0000

(-15.2290) (-5.7506) (-1.2194) (-1.700) (-1.1416) (-0.5784) (0.8267) (-1.4320)

从下跌阶段的回归结果来看，当期的期货收益率受到滞后1期和滞后7期的期货收益率的显著影响，同时也受到滞后3期和滞后7期的现货收益率的显著影响。而当期的现货收益率受到滞后1、2、3期的期货收益率的显著影响，也受到滞后1、2期的现货收益率的显著影响。这说明在下跌阶段，现货收益率与期货收益率会互相影响，二者都会根据过去的期货收益率和现货收益率进行调整。

2.3 Granger因果检验

Granger因果关系检验是建立在VAR模型基础上的，我们构建如下方程检验沪深300股指期货与现货之间的因果关系及其影响方向:

(2)

(3)

式(2)和式(3)中：st、ft为收益率序列当期值；st-i,ft-i为收益率序列滞后i期的值；αi,βi,λi,δi为回归系数；ut、vt为误差项。由于不同的滞后阶数会对回归结果产生影响，所以根据建立VAR模型时最优滞后期的选择，上涨趋势的最优滞后期为4，下跌趋势的最优滞后期为7。结果见表5。

表5 Granger因果关系检验结果

由表5的结果可以看出，在上涨趋势中，不存在现货收益引起期货收益变化的Granger因果关系，而存在期货收益引起现货收益变化的Granger因果关系。在下跌趋势中，存在现货收益与期货收益相互引导的Granger因果关系。这个结论与VAR模型的回归结果是一致的，在上升阶段，期货收益率不受现货收益率滞后期的影响，而现货收益率受期货收益率滞后期的影响，在下跌阶段，二者互相影响。

2.4 脉冲响应函数

Granger检验虽然验证了在上涨和下跌阶段时，沪深300股指期货与沪深300指数现货之间的引导关系，但没能检验出两者之间价格发现能力的强弱。因此下文将应用脉冲响应分析方法进一步探究沪深300股指期货收益与沪深300指数现货收益之间的相互影响。图1、图2分别给出了上涨阶段和下跌阶段的脉冲响应函数的分析结果(图中RS代表沪深300指数收益率，RF代表沪深300股指期货收益率)。

从图1中可以发现：期货市场和现货市场对来自自身的冲击反应均较为迅速，均会在当期做出反应(脉冲响应图里的期限“1”指当期，期限“2”为滞后1期，依此类推)，但期货市场能够在5分钟内基本消化完毕，而现货市场则需要10分钟左右的时间来完成大的调整。然而它们完全消化和吸收来自自身冲击的时间较长，一般要持续6期左右(约30分钟)。对期货和现货市场之间的冲击而言，影响的程度和时间存在较大差异，现货市场的冲击对期货市场几乎不产生影响。期货市场的冲击对现货市场具有很强的正向影响，且持续时间较长。图2中的趋势与图1基本一致，只是在下跌趋势中，信息消化和调整的时间更长。

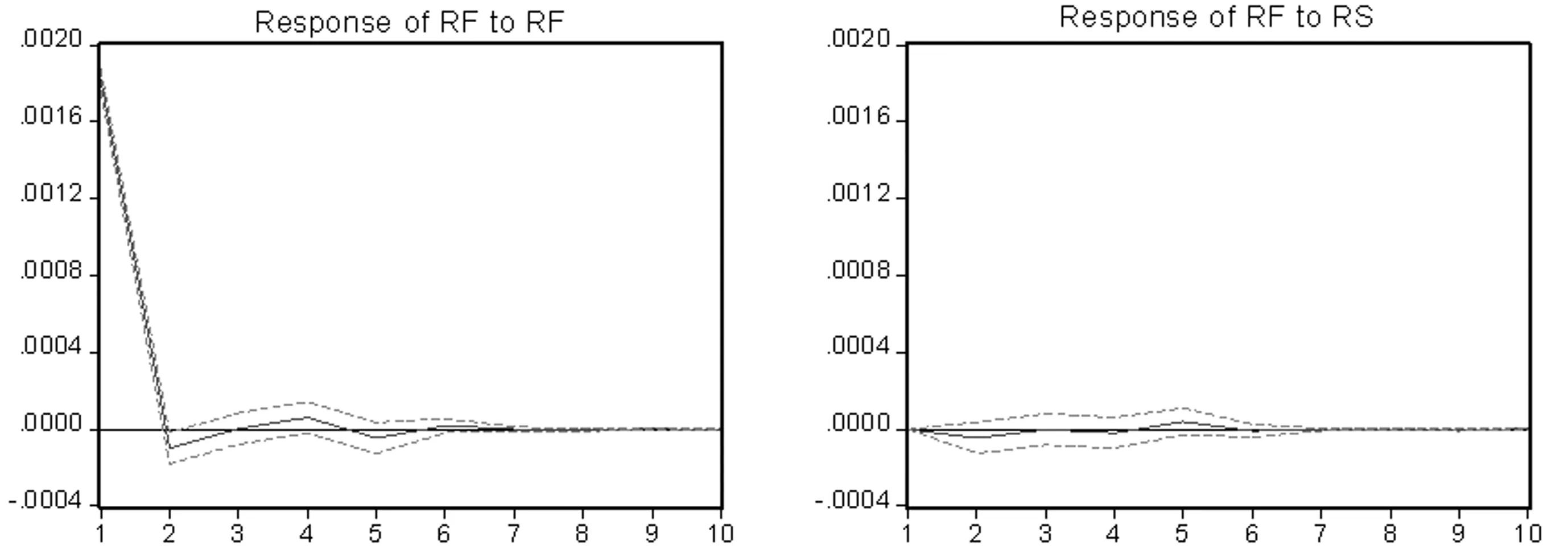
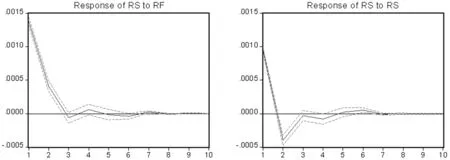
图1 上涨阶段的脉冲响应函数

图2 下跌阶段的脉冲响应函数

2.5 Hasbrouck方差分解

为了进一步刻画期货市场与现货市场在价格发现功能中贡献度的大小，我们利用Hasbrouck[23]提出的方法进行方差分解。表6和表7分别给出上涨阶段和下跌阶段方差分解结果。从表6中可以看出，在上涨阶段，对于期货市场，在滞后1期时，期货价格总方差全部由自身价格扰动所引起的，然而，从第二期开始，随着滞后期的增加，总方差中来自于期货市场的部分开始减少，最终趋于99.88%左右，而来自于现货市场的则不断上升，最终趋于0.12%左右；而对于现货市场，当滞后期为1时，总方差中有67.8144%来自于期货，32.1856%来自于现货，最后来自于期货市场的逐渐减少，趋于65.97%左右，来自于现货市场的逐渐增加，趋于34.03%左右。

从表7中可以看出，在下跌阶段，对于现货市场，在滞后1期时，期货价格总方差全部由自身价格扰动所引起的，然而，从第二期开始，随着滞后期的增加，总方差中来自于期货市场的部分开始减少，最终趋于99.69%左右，而来自于现货市场的则不断上升，最终趋于0.31%左右；而对于现货市场，当滞后期为1时，总方差中有73.6951%来自于期货，26.3049%来自于现货，最后来自于期货市场的逐渐减少，趋于70.62%左右，来自于现货市场的逐渐增加，趋于29.38%左右。

表6 上涨阶段的方差分解

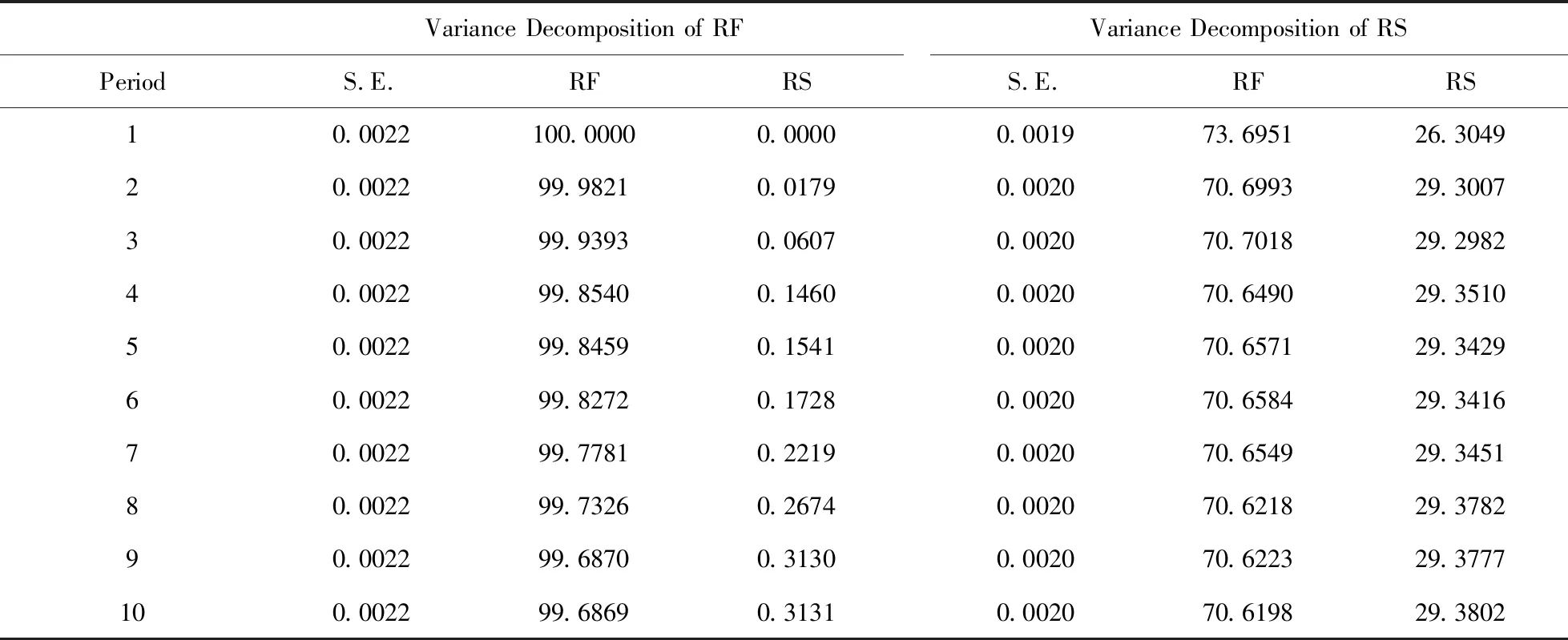
表7 下跌阶段的方差分解

综上，在上涨阶段中，来自于期货市场的方差平均数为82.925% ((99.88%+65.97%)/2)，来自于现货市场的方差平均数为17.075%((0.12%+34.03%)/2)；在下跌阶段中，来自于期货市场的方差平均数为85.155%((99.69%+70.62%)/2)，来自于现货市场的方差平均数为14.845%((0.31%+29.38%)/2)。因此可以发现，无论是上涨阶段还是下跌阶段，沪深300股指期货在价格发现功能都处于主导地位，并且在下跌阶段，股指期货的价格发现功能要稍强于上涨阶段。

2.6 Johansen协整检验与向量误差修正模型

前面内容都是基于收益率数据进行的分析，下面进一步利用价格数据来分析沪深300股指期货与现货价格的长短期关系。前文的单位根检验已证明和是一阶单整过程，所以可以借助Johansen协整检验。我们选择含截距项而不含趋势项的Johansen协整检验进行分析，滞后阶数根据AIC准则选取14阶。由表8可知，在上涨阶段S和F下跌阶段，沪深300指数现货与期货价格之间均存在着1个协整向量，说明虽然沪深300股指期货价格与现货价格都是非平稳的时间序列，但是它们之间存在长期稳定的均衡关系。

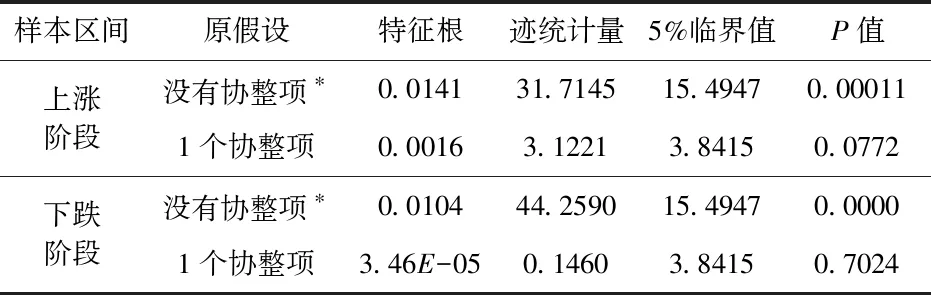
表8 沪深300现货价格与期货价格的Johansen协整检验结果

由上述分析可知，股指期货价格与现货价格存在协整关系，所以我们可以用向量误差修正模型(VECM)刻画二者之间的短期非均衡关系。VECM是将协整与误差修正模型结合起来建立的一种模型。S和F的向量误差修正模型为：

(4)

(5)

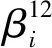
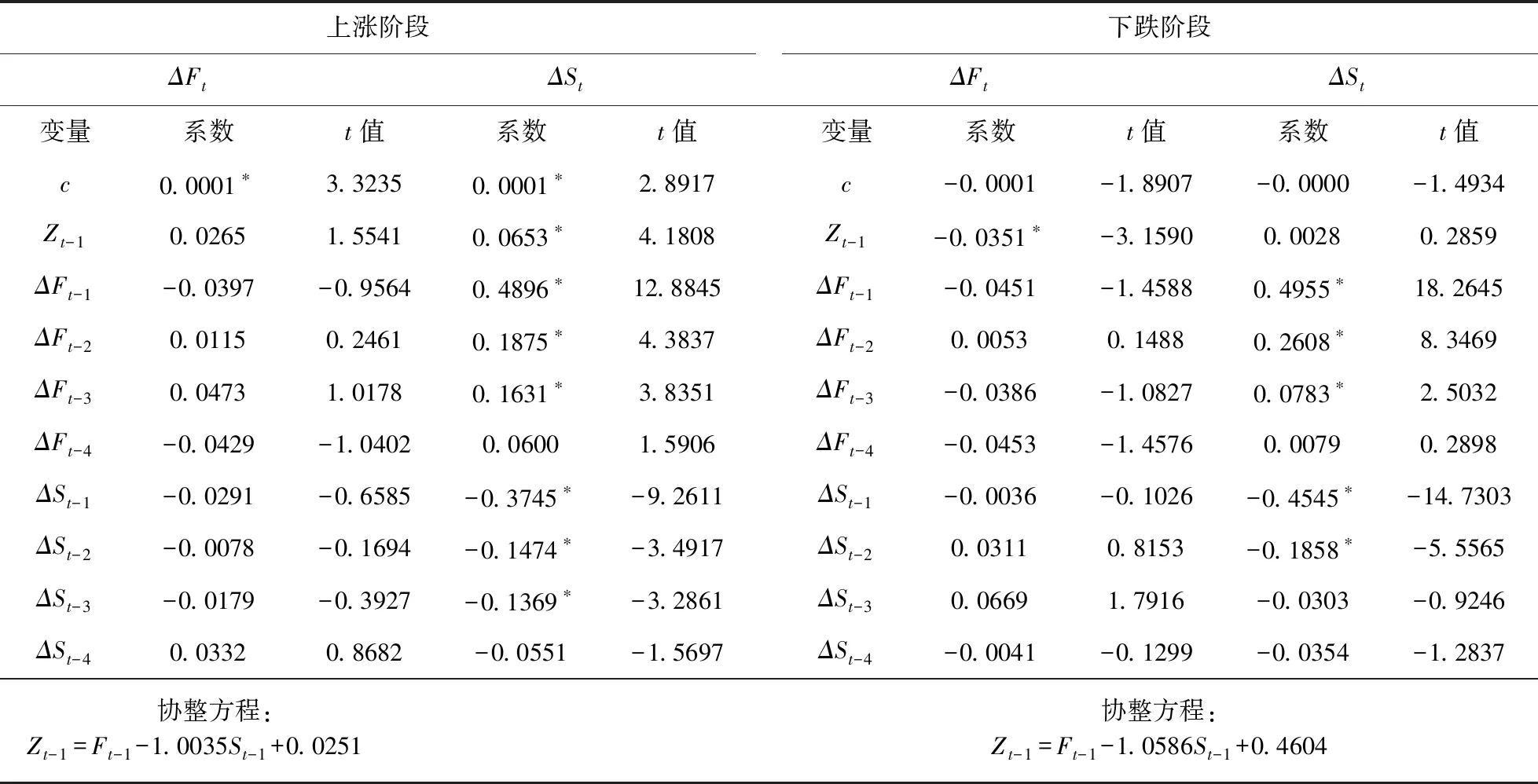
表9 VECM模型回归系数表

3 结论

本文利用沪深300股指期货和现货的高频数据，研究我国股指期货的价格发现功能，得出如下结论：向量自回归模型与Granger因果关系检验结果发现，在上涨趋势中，期货收益率具有单向影响现货收益率的作用，在下跌趋势中，二者存在相互的Granger因果关系。通过脉冲响应函数研究得出，短期内期货受到来自现货市场冲击的影响有限，而现货受到来自期货市场冲击的影响较大且调整时间长。方差分解进一步说明无论是上涨阶段还是下跌阶段，沪深300股指期货在价格发现功能都处于主导地位。协整检验和VECM分析说明，无论是上涨阶段还是下跌阶段，沪深300股指期货与现货之间存在长期均衡关系；短期出现非均衡状态时，现货价格受期货价格引导向均衡状态调整。因此沪深300股指期货市场在上涨和下跌过程中都具备价格发现功能，并且在价格发现中处于主导地位。