一种改进的k-modes聚类算法

施振佺 陈世平

(1.上海理工大学 管理学院,上海 200093； 2.南通大学,江苏 南通 226019)

0 引言

聚类是将相似度较高的数据对象分成相同类的过程。它通常是通过计算不同数据对象之间的相似度来判断他们属于哪个类，将相似度较高的分在同一个类，从而进行分类的过程。聚类是数据挖掘的一个重要研究方向。现实中聚类分析的数据对象有不同的类型，可以分为数值型、分类型、数值和分类混合型。针对三种处理数据对象的类型分别有三种代表性的聚类方法，是K-means算法[1]、K-modes算法[2]和K-Prototype算法[3]。HUANG ZX[2]在K-means算法基础上提出了K-modes算法，该算法改进了k-means算法中采用距离作为度量的问题，而采用了相异度来度量。算法通过计算样本和聚类中心的相异度来进行聚类，相异度越小，则表示属于这个类的可能性越大。

K-modes算法给分类型对象带来了一种新的解决无法像数值型对象那样计算距离的新方向，但考虑到HUANG ZX来计算分类对象属性值间距离时仅采用了简单的“0-1”匹配方法，虽然这种方法计算简便也能很容易被应用在各种领域，但这种算法谈话了对象类属性内部的相似性问题，因此He[4]、San[5]、Ng[6]等人提出了属性值在类内出现的频率来计算两个属性值之间的距离。Hsu等人[7,8]通过计算对象层次的距离提出了一种新方法，但主要依靠专家的经验和专业技术知识。Ganti等人[9]和Ahmad等人[10,11]用同一属性下不同对象值之间的贡献程度来计算他们之间的距离，但该方法没有考虑属性自身的差异。这些研究都在K-modes 算法改进了对同一属性下不同对象的聚类能力，但忽略了对象的不同属性间的差异。

近些年来，一些学者研究通过加权属性来解决聚类对象不同属性之间的差异问题，从而确定分类型对象之间的相异度，达到聚类的效果。梁吉业等[12]提出了基于新的距离度量的K-Modes聚类算法，该距离度量算法在度量同一分类属性下两个属性值之间的差异时, 克服了简单0-1 匹配差异法的不足, 同时考虑了属性自身及同其它属性的异同，但是算法研究的是每个属性值之间的差异，另外在计算类中心点是仍然用的原来的频率计算的方法来计算聚类中心点，所以该算法的效率不是特别高。白亮等[13]通过用粗糙集理论来计算聚类对象间的距离，张小宇等[14]通过连接度来计算聚类对象属性间的距离，Dino Ienco等[15]应用条件概率差来计算聚类对象属性值之间的距离,这些研究的实验结果均改善了聚类对象的聚类效果，但这些方法都很高的计算复杂度问题。李仁侃[16]提出了自动属性赋值的K-Modes算法，该算法将Huang等人[17]提出的变量自动加权聚类算法(weighting in K-Means, W-K-Means)运用到K-Modes同属性权重相结合的算法上来，能解决K-Modes算法在不同属性间的异同问题，但是该属性加权是主要基于数值型对象，对于分类型对象相对较弱，同时算法的效率也相对较弱。吴润秀[18]和黄苑华等[19]都运用了互信息理论来确定各个对象属性的权重，然后加权到相异度上，从而解决了各属性间异同问题，但是他们在确定属性权重时更多考虑的是两两属性之间的关系，而在所有属性之间的影响关系上较弱。

本文利用粗糙集理论无监督学习和综合各属性差异的优点，同时采用知识粒度来克服粗糙集计算不够精细的问题，来计算分类型对象各属性的权值，以此结合Ng[6]等人提出的K-Modes聚类算法，可以解决聚类对象不同属性对聚类的影响，使聚类结果更加精确。

1 经典的k-modes算法

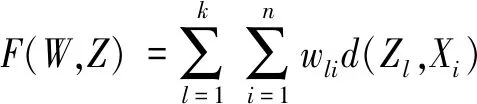
其中

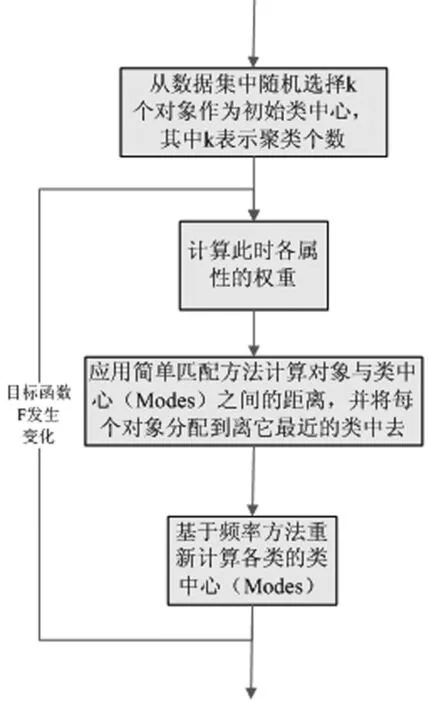
K-Modes聚类算法的基本步骤如下：

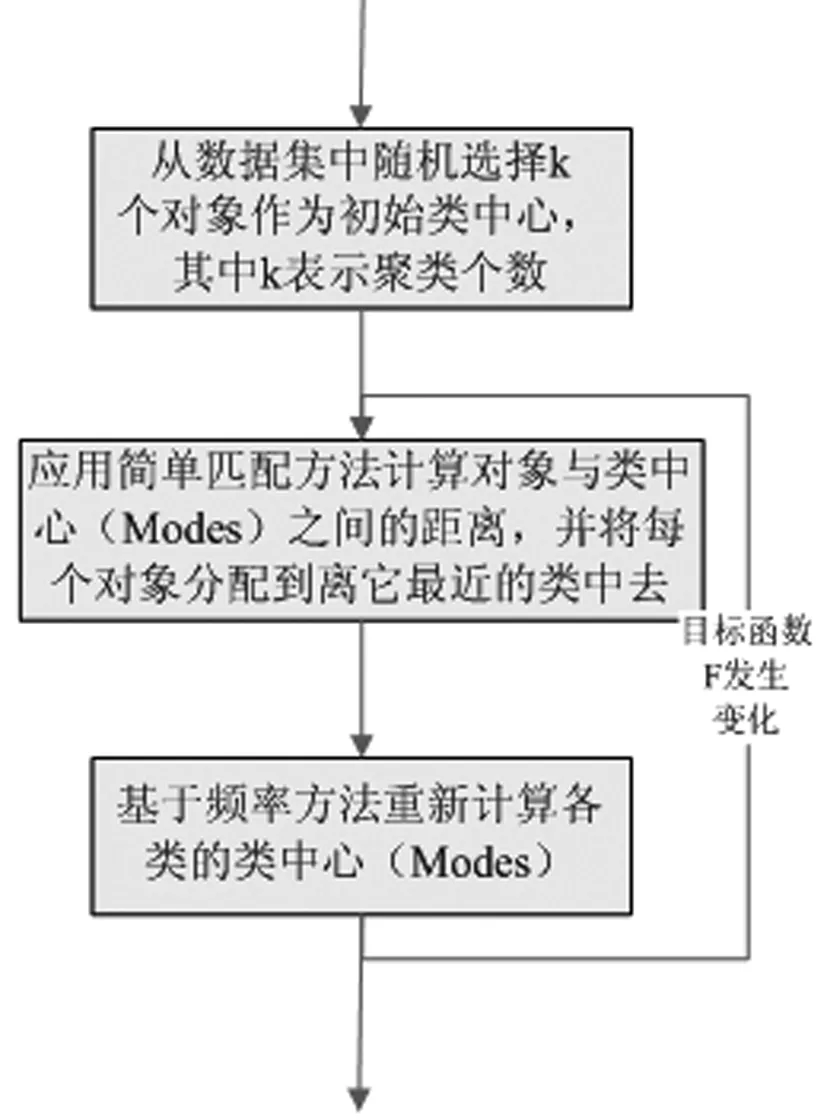
3 粗糙集和知识粒度概念

3.1 粗糙集

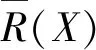
在U上的等价关系P、Q中，若P⊆Q，那么对于∀x∈U，有[x]P⊆[x]Q。则可以认为等价关系P对对象论域U的划分U/P相对于等价关系Q对对象论域U的划分U/Q要更加精细，那么知识库(U,P)相对于知识库(U,Q)对于对象论域U的描述要更为精确。

3.2 知识粒度

基于粗糙集理论的进一步发展，人民普遍认为知识与这种等价关系以及由等价关系而产生的等价类是相关的，这就表明知识是有粒度的。因此，国内外有些学者也通过等价类和等价关系来表示知识的类似颗粒状结构，并计算出由等价关系和等价类表示出来的知识知识粒度的大小[23～30]。

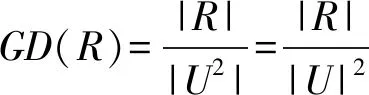
4 改进的k-modes算法

Indrajit Saha等[31]人利用粗糙集和模糊集知识来对分类型数据对象进行聚类，该算法对聚类起到一定的改进效果，但是该算法没有考虑各属性之间的相互关系，所以在使用该算法时效果相对较弱。

表1列出的是Indrajit Saha文章的表2数据，按照Indrajit Saha提出的算法D(c1,x1)=77/45，D(c2,x1)=79/45 ，D(c3,x1)=84/45。但是我们将x7，x8，x9改成(C,D),(A,D)，(A,E)，那么计算出来数据对象和聚类中心的距离D’(c1,x1)=79/45，D’(c2,x1)’=77/45 ，D’(c3,x1)=84/45，这时对应的x1就会被归类到Cluster2(c2)中，而这里聚类Cluster1(c1)和Cluster2(c2)的中心没有变化，数据对象也没有变化，只是聚类Cluster3(c3)中的数据对象有些变化却导致了原本属于聚类Cluster1(c1)的数据对象却归类到了聚类Cluster2(c2)。导致这个问题的原因是没有考虑属性A1和A2对聚类的影响，于是考虑对聚类数据的属性进行加权来解决数据对象各属性间的差异问题，本文将运用粗糙集和知识粒度理论来确定数据对象各属性的权重。

表1 An artificial data set for Indrajit Saha’s paper

4.1 基于粗糙集和知识粒度的特征权重确定

设I=(U,A)是一信息系统，R⊆A是一特征子集，r∈A是一特征，我们考虑特征r对于U的分辨度，是R中增加特征r之后分辨能力提高的程度，即分辨度的提高程度。分辨度提高程度越大，认为r对于R分辨能力越强。为此，有如下定义

定义1设R⊆A为一特征子集，r∈A为一特征。设U/R={X1,X2,…,Xn},U/(R-{r})={Y1,Y2,…,Yn}。r对于U的分辨度，记为Dis(r)，定义Dis(r)=Dis(R)-Dis(R-{r})。

上述定义理解为，在对象论域U中任取两个对象，那么一共有|U|2种选取方法。如果在特征集(R-{r})中增加了某个特征r之后，那么它的不可分辨的情况将由|(R-{r})|增加到|R|种，这说明通过等价划分所产生的等价类的集合数量要比原来多了，这样可分辨的能力就比原来增加了，分辨度也就相对原来的分辨度有所提高了。

定理1设r∈R，设U/R={X1,X2,…,Xn}，U/(R-{r})={Y1,Y2,…,Ym}，Dis(r)为r对于U的分辨度，则有0≤Dis(r)≤1-1/|U|。

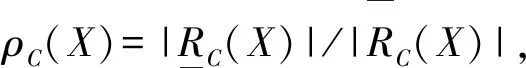
KCDis(C)=ρC(X)×Dis(C)

=ρC(X)×(1-GD(C))

定理2X=U/D={X1,X2,…,Xn}为论域U在决策特征D下的等价分类集，对于条件特征(属性)中∀c∈C，KCDis(c)为c对于U的分辨度，则有0≤KCDis(c)≤1-1/|U|。

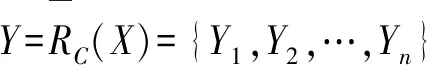
KCDis(c)=KCDis(C)-KCDis(C-{c})

=ρC(X)×Dis(C)-ρC-{c}(X)×Dis(C-{c})

定理3X=U/D={X1,X2,…,Xn}为论域U在决策特征D下的等价分类集，对于条件特征(属性)中∀c∈C，KCDis(c)为c对于U的分辨度，则有:

(1)设P、Q是U上的等价关系，若P⊆Q，那么有KCDis(P)≤KCDis(Q)；

(2)0≤KCDis(c)≤1-1/|U|。

4.2 改进的k-modes算法

本文将提出一种基于粗糙集和知识粒度的属性加权算法来改进k-modes算法，该算法利用属性权重计算方法来计算不同属性对聚类算法的影响程度，从而加权到相异度的计算中，来确定数据对象和聚类中心的相异度。

对于数据对象集合X={X1,X2,…,Xn}和数据对象的属性集A={A1,A2,…,Am}，定义目标函数为

其中

wli∈{0,1},1≤l≤k,1≤i≤n

对于例1中的情况就有D(c1,x1)=88/162，D(c2,x1)=125/162。但是我们将x7，x8，x9改成(C,D),(A,D)，(A,E)，那么计算出来数据对象和聚类中心的距离D’(c1,x1)=44/81，D’(c2,x1)’=50/81,故x1被归类到 Cluster1(c1)中。

于是改进的K-Modes聚类算法步骤如下:

5 实验分析

下面分别从分类正确率(accuracy )、分类精度(precision)、召回率(recall)3个方面[32]来分析算法的聚类质量:Accuracy(AC), Precision(PE), Recall(RE)分别定义如下:

其中，n表示数据库中的聚类对象数，ai表示第i类中正确的对象数，bi表示第i类中错误的对象数，ci表示应该分到第i类却被分到其它类的对象数，k表示所形成的聚类个数。我们从UCI数据集中挑选了3组对象数据，具体的数据描述见表2所示，并将我们改进的K-Modes聚类算法分别与Huang和Indrajit Saha的K-Modes算法进行比较。

表2 Description of the used data sets

分别运用三种算法对表2中的数据对象进行计算，通过平均聚类质量来验证算法的有效性。则比较得出表3～5的结果。

表3 在Congressional Voting Records下的算法性能比较

表4 在Balance Scale下的算法性能比较

表5 在Solar-Flare下的算法性能比较

通过分析表3～5，在数据Congressional Voting Records, Balance Scale和Solar-Flare上,本文改进的聚类算法在聚类过程中相对于其它聚类算法取得了比较好的效果，因此根据实验结果表明改进的聚类算法是有效的。

6 结论

本文改进了K-Modes聚类算法，提出了基于属性加权的K-Modes聚类算法。该属性加权算法运用了粗糙集和知识粒度概念，同时考虑了属性的冗余性，又考虑了数据对象的各种属性间的差异。通过改进传统的K-Modes聚类算法，增加属性加权算法，并与传统的K-Modes聚类算法进行实验比较，实验结果说明改进的K-Modes聚类算法在总体上的表现优于其它的K-Modes聚类算法，它能很好的改善聚类效果。