考虑双方感知满意度的应急资源再配置方法
2019-10-27李怀明王佳美
李怀明, 王佳美, 张 磊
(大连理工大学 经济管理学院,辽宁 大连 116024)
0 引言
近年来有相当一部分次生灾害破坏效果巨大,甚至高于原生灾害带来的损失,呈现出受灾点多、物资需求量大以及供应不足等特点。如2008年汶川地震引发的多处堰塞湖灾害、日本九级地震引发的福岛核电站泄漏事件等,对次生灾害的应急处置越来越受到重视。在次生灾害发生后,外界资源不能在短时间内迅速到达灾区,此时需要发挥区域互救的地理优势,紧急将原生灾害点的部分应急资源供应于次生灾害点,这对处于灾情初期、资源极度紧缺的次生灾害点来说非常重要。因此,充分利用各灾区间相距较近的地理优势展开互救行动,对灾区间现有应急资源进行再次配置是做到有效救援,及时响应的方法之一。

现有研究中一些学者尝试将灾民心理因素融入到突发事件应急决策中,如KM Kowalski等[9]将危机事件集体减压法(CISD)应用到应急救援中,结果表明该方法可显著提升救援行动效率。王旭坪等[10]将行为科学引入应急物资调度,用前景理论量化公众风险感知程度。王治莹等[11]考虑公众的有限理性,运用前景理论刻画舆情传播中公众对应急资源供应量的风险感知行为。在刻画受灾点满意度方面,Mohammadi R等[12]根据不同情景下的期望需求刻画受灾点满意度,并以最小化满意度作为目标之一,构建了一个多目标模型并通过改进多目标粒子群算法进行求解。宋晓宇等[13]将受灾点需求紧迫度系数引入到受灾点满意度函数中,用以描述不同受灾点对相同物资缺失比率持有不同的满意度,最后通过设计一个混合多目标粒子群算法求解出调度方案。曲冲冲等[14]考虑到物资配送两阶段过程中的时效性与分配公平性,用线性函数刻画应急时间满意度来构建选址与路径优化的多目标规划模型,并设计了带精英策略的非支配排序遗传算法求解。
上述研究成果对应急资源配置问题中灾民心理的刻画提供了很好的研究基础。在区域互救下的应急资源再配置中,由于原生灾害点是临时资源供应点,资源的损失将会降低灾区的救援保障,因此势必要考虑到该区域灾民的不满情绪,从而不能毫无保留的共享。次生灾害点作为资源需求方,更关注的是资源是否能及时响应,供需双方在对待再配置问题的心态上是存在明显不同的。然而,现有研究中没有从该角度对资源提供与接收双方灾民的心理感知满意度进行详细刻画。因此,考虑到区域互救的应急资源再配置中原生灾害点和次生灾害点灾民心理感知的不同,本文在现有研究基础上,构建了原生灾害点灾民对于应急资源的需求感知满意度价值函数和次生灾害点灾民对救援时间感知满意度函数,提出了最大化救援双方灾民感知满意度和最大化单位时间运输量为目标的优化模型,采用改进的多目标粒子群仿生算法对模型进行求解,并对比物资储备中心作为供应点的配置问题,以期为突发事件应急决策部门制定灾害链中的应急资源配置提供决策支持。
1 应急资源再配置模型
1.1 问题描述与假设
灾害在演化过程中形态易发生变化,对于应急资源的需求量会随时间呈现脉冲式的变化[15]。图1展示了再配置问题的一个情景,灾害发生后应急资源需求剧增,t1时刻物资储备中心大规模供应资源G1,在灾情有所控制的情况下,t2时刻又发生了次生灾害,各受灾点在时间上有先后,在空间上彼此相依,在成因上相互关联,互为因果,呈连锁反应依次出现[16]。基于应急协作区域联动机制[17]和资源后续共享原则,整合原生灾害点总应急资源量G2,将资源量Q=G2-R共享给次生灾害点,剩余资源量R继续执行救援任务,实现对现有应急资源的再配置。在t3时刻到达次生灾害点开始救援行动,虽然未满足次生灾害点实际需求,但却在第一时间响应了次生灾害,为后续大规模救援行动争取了宝贵的时间。应急资源的再配置使得原生灾害点灾民失去了部分救援保障,由此所感知的不满意度,应当在再配置模型中有所体现。
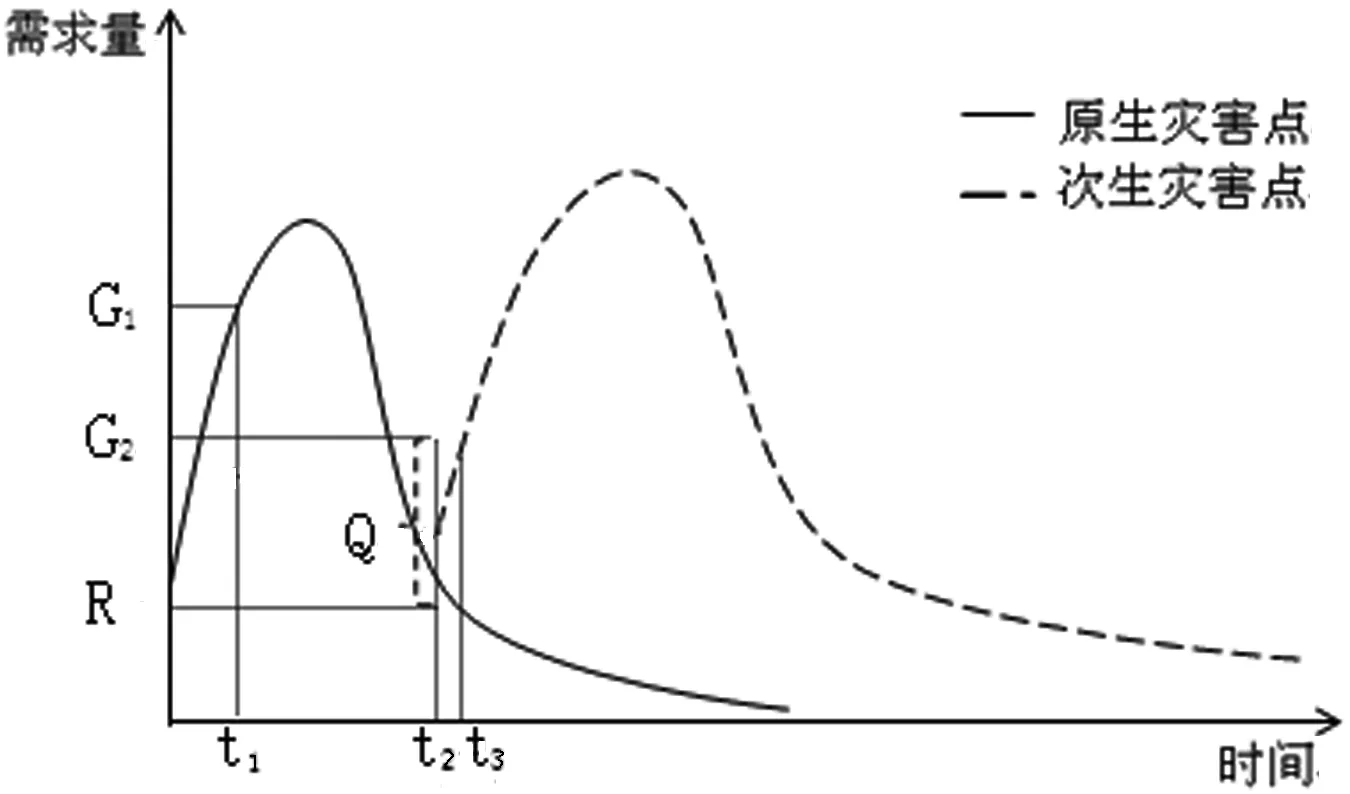
图1 应急资源需求随时间变化情况
基于以上问题情景,设区域M突发地震造成多个原生灾害点A={a1,a2,…,am},在第一批应急资源抵达,并基本控制住灾情的情况下,又因余震、泥石流、堰塞湖等不可控因素诱发了多个次生灾害点B={b1,b2,…,bn},如图2所示。在外界大规模应急资源和救援行动到达之前,充分利用应急资源开展区域互救是提高灾害应对水平和减少灾害损失的重要手段。设原生灾害点ai在确保自身灾情可控下,紧急共享一部分应急资源救援次生灾害点bj,i=1,2,…,m,j=1,2,…,n。如原生灾害点a1可以向b1,b2,b3次生灾害点提供应急资源。
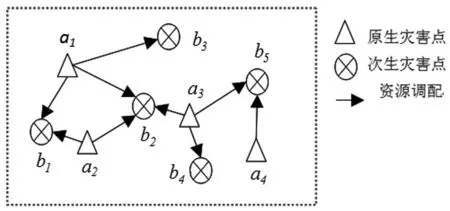
图2 灾害链内应急资源配置示意图
因地震的发生具有巨大破坏性和不确定性,本文需要在建立模型之前做出以下假设:
1)原生灾害点已基本完成第一时间的紧急救援行动,如道路清理等工作,可以在特殊情况下临时共享一部分资源支援次生灾害。
2)原生灾害点应急资源的最大共享量和次生灾害点的资源需求量可以根据灾区当前情况、灾害类型和发生强度等因素估计出来。
3)应急资源均一次抵达,运送时间和运送资源的多少无关。而运输时间的估计值可以根据以往救援经验和先进地理信息技术得到,暂不考虑因道路破坏等外界因素对运输时间的评估。
1.2 灾民感知满意度分析
基于人的有限理性,公众对满意度的感知是受主观感受和认知所影响的[18]。在突发事件下会存在得失心态严重放大、追求“公平”、存在“攀比”等不确定性行为。原生灾害点作为临时的应急资源供应点,与物资储备中心的区别在于需要考虑灾民的感知满意度从而不能毫无保留的供给。而次生灾害点作为资源需求方,更希望能在短时间内获得大量应急资源以保障灾情不再继续扩大。供需双方灾民此时的心理情境不同,对不同因素的敏感性不同,需要区别对待,因此本文将灾民的感知满意度分为原生灾害点灾民需求感知满意度和次生灾害点灾民时间感知满意度。
1.2.1 需求感知满意度
对应急资源需求的满意度感知问题在应急管理领域中较为常见,一般可以用物资满足率[19]、效用函数[20]等来度量。原生灾害点作为灾害链中的前序阶段,此时响应时间已不再是最为关键的因素,其对应急资源配置的满意度感知主要来源于应急资源的数量。数量的减少意味着救援能力的降低,带来的是更严峻的生命威胁和恐慌情绪,感知满意度也随之降低。在突发灾害这一特殊情形下,资源的损失将比获得更加敏感,对应急资源的再配置会给原生灾害点灾民带来心理落差,可能导致不满情绪。借鉴前景理论的价值函数[21],本文将原生灾害点灾民对于应急资源的需求感知满意度价值VI描述为:
(1)
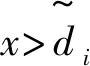

图3 需求感知满意度曲线
1.2.2 时间感知满意度
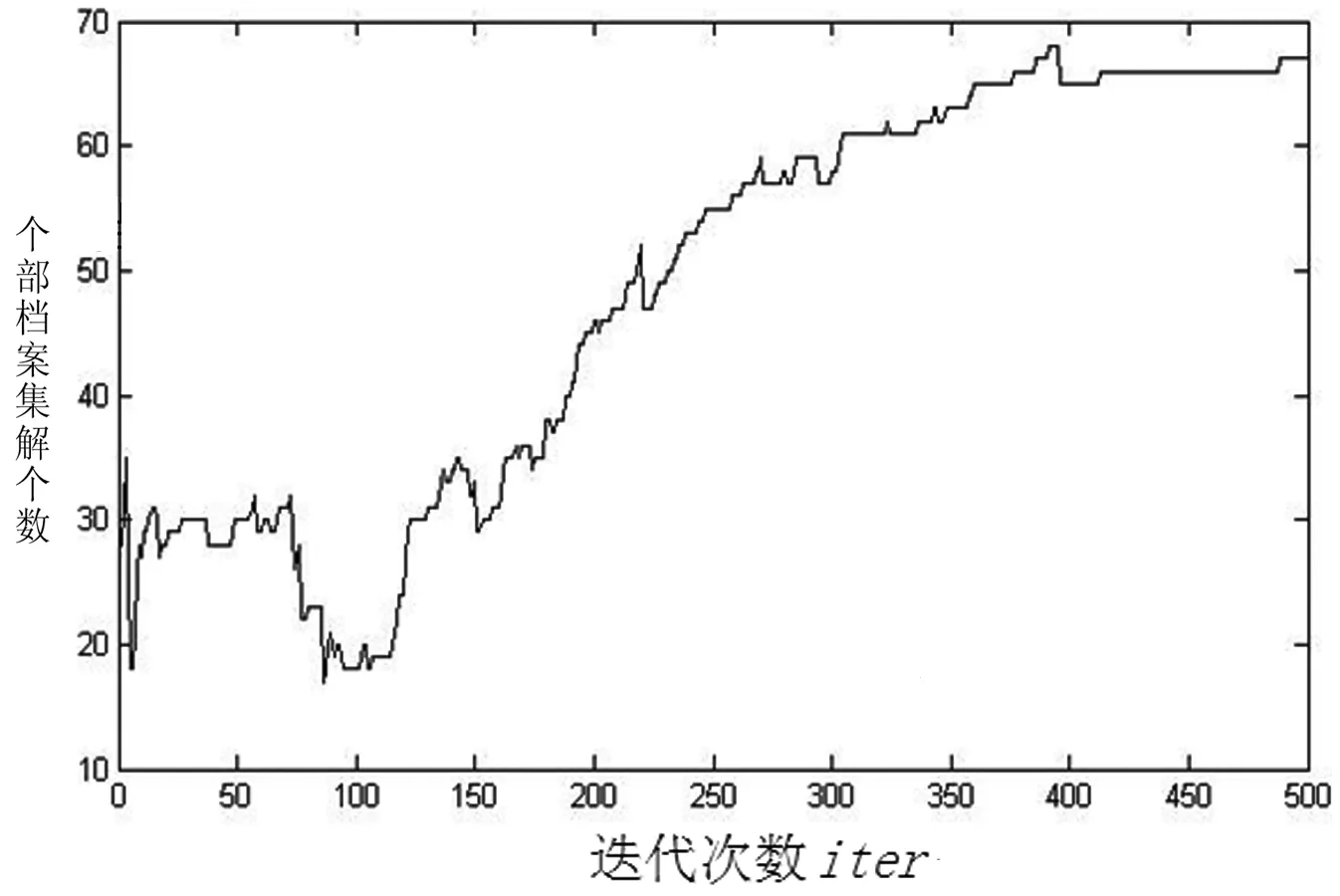
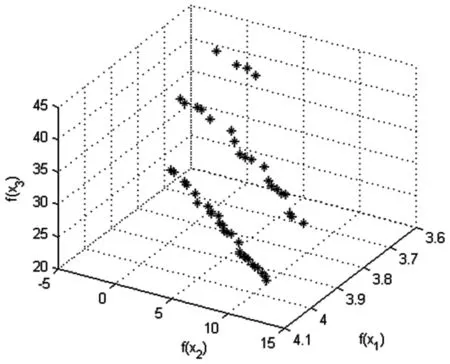
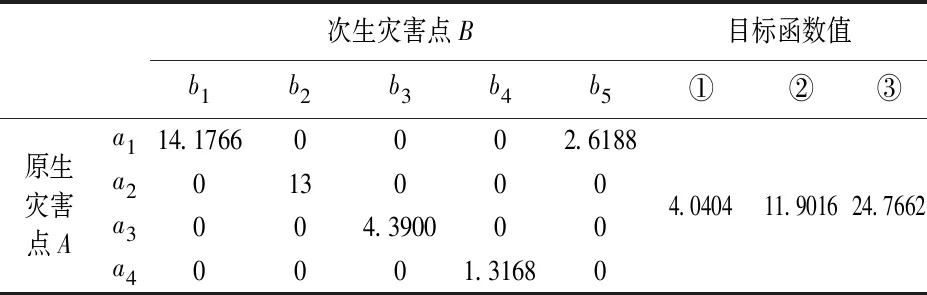
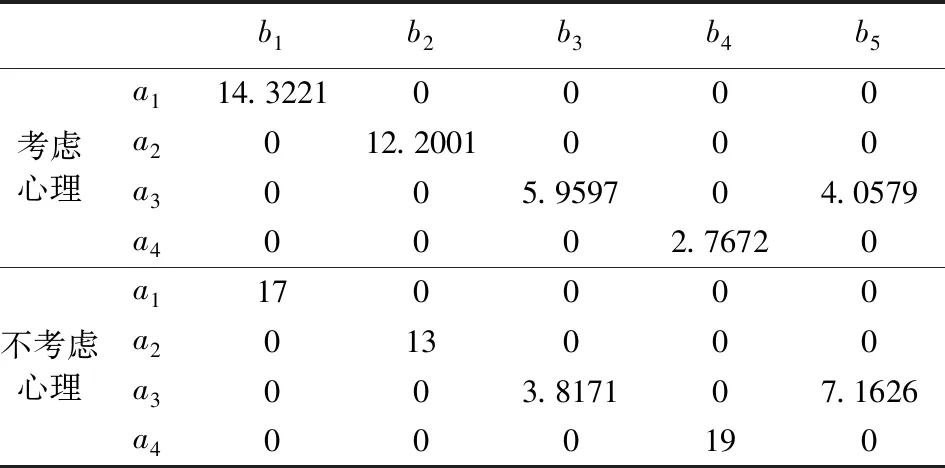
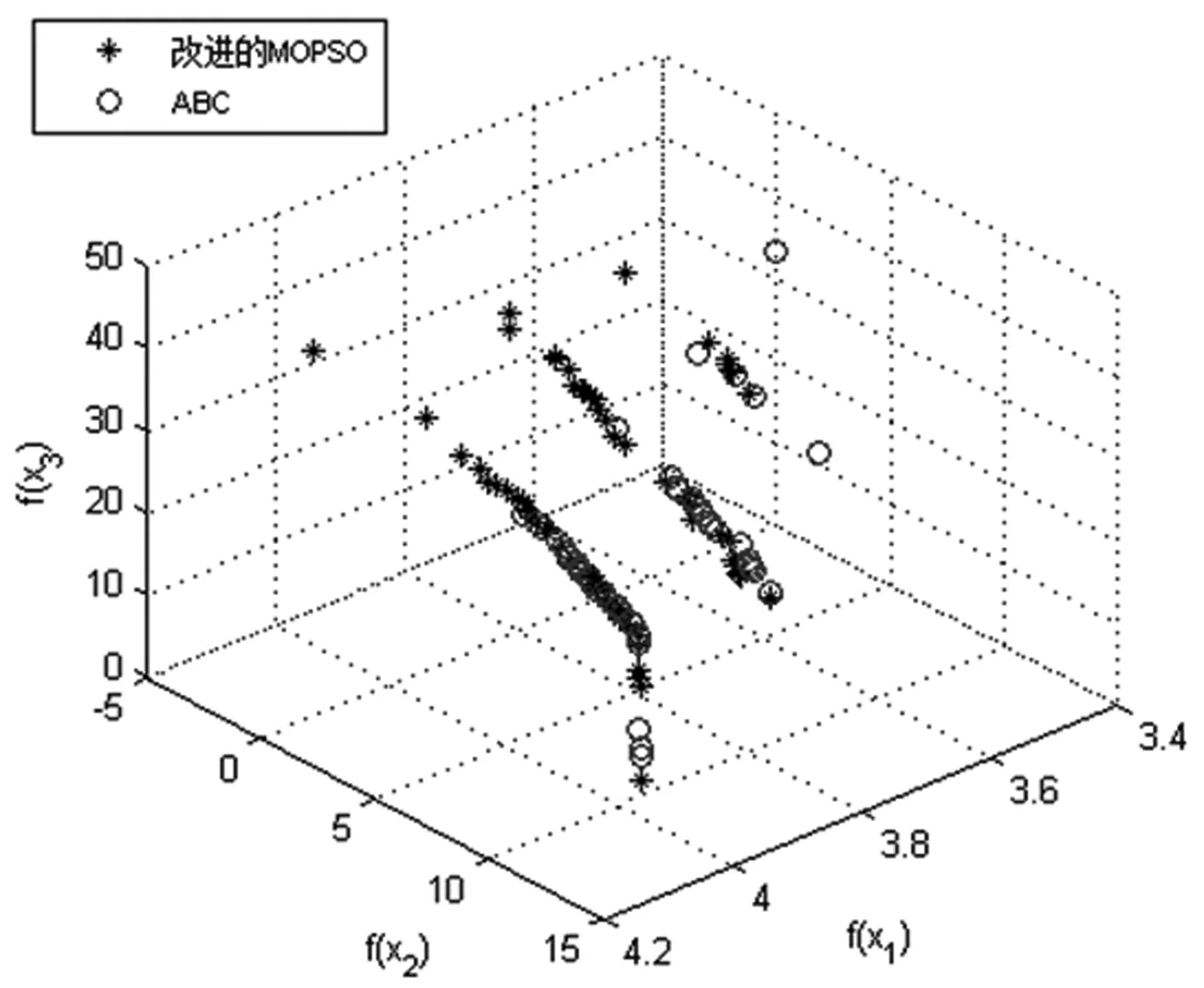
在第一时间的区域互救过程中,资源需求得不到满足,需要等待后期大规模的救援资源抵达,因此次生灾害点灾民对第一批应急救援的到达时间更为敏感。这种对应急响应时间的感知与灾民在灾害发生后的生存概率息息相关,响应时间越短,灾民的生存概率越大,对应急救援行动越满意。Hong Chi等人对应急资源调度中的时效性评价函数应用到了sigmoid函数,这种单调递减的平滑曲线可以根据适当调参去很好的模拟应急救援中的特殊状况[22]。由此对时间感知满意度的刻画可以引入Fiedrich等人根据几次地震发生后被困人员生存概率随时间变化的大致形态[23],以及Sung构建的治愈概率函数[24]来推测出时间感知满意度曲线。本文对受灾点bj的救援时间感知满意度gj随应急资源到达时间t(0 (2) 其中,θj(θj>0)与次生灾害点bj对应急资源的需求紧迫度相关,值越小,表明运送的应急资源对bj越重要,需求越紧急。如图4展示θj=20时的时间感知满意度曲线,在前20%的时间内生存概率极高,灾民感知满意度较大,救援效果最佳,后30%生存概率则一直走低,救援响应时间的加快对灾民感知满意度的影响较小,此时的救援效果最差。中间50%是灾民对应急响应时间最为敏感的一段时间,此时灾民情绪波动较大,需要在救援行动中争分夺秒,以微小的响应时间加快带来灾民感知满意度的大幅提升。 图4 时间感知满意度曲线 由于原生灾害点是临时供应点,运输工具也是稀缺资源,所以为了体现对有限资源的充分利用原则,本文将最大化单位时间运输量也作为优化目标,构建了以最大化原生灾害点和次生灾害点双方感知满意度、最大化单位时间运输量为目标的多目标应急资源再配置模型。 相关符号及变量说明: 原生灾害受灾点集合I={1,2,…,m}。 次生灾害受灾点集合J={1,2,…,n}。 xij为从原生灾害受灾点ai到次生灾害点bj的应急资源运输量,i∈I,j∈J。 yij为1表示从原生灾害受灾点ai运送应急资源到次生灾害点bj,为0表示不运送。 tij为原生灾害点ai到次生灾害点bj的运输时间。 各个原生灾害点应急资源最大共享量为M={Mi},i∈I。 各个次生灾害点应急资源需求量为D={dj},j∈J。 c为单位时间运输量的最小临界值。 考虑灾民感知满意度的应急资源再配置模型如下: (12) 其中,式(3)表示最大化次生灾害点时间感知满意度。式(4)表示最大化原生灾害点需求感知满意度。式(5)表示最大化单位时间运输量,以保证运输工具充分利用。式(6)表示选取最大运输时间作为次生灾害点救援行动的开始时间。式(7)表示分配给次生灾害点的应急资源应不超过其实际需求。式(8)表示从原生灾害点共享的资源量不超过其最大提供量。式(9)表示原生灾害点ai到次生灾害点bj的单位时间运输量低于临界值c则ai不能向bj运送资源。式(10)表示每个次生灾害点都有分配到资源。式(11)表示从原生灾害点i分配资源到次生灾害点j则将yij置为1,反之记为0。式(12)为限制变量的非负约束和0-1约束。 本文所建立的模型是在区域互救行动的客观事实上,以最大化原生灾害点和次生灾害点的感知满意度为主要目标,为保证运输工具有效利用,将单位时间的运送量作为第三目标,进而建立了问题的多目标规划模型,一般求解该类多目标问题的方法有:加权求和法、目标规划法、分层序列法、Pareto最优性分析等。由于模型目标表示的实际意义相差甚远,单位较难统一,且彼此矛盾,将目标函数归一化的方法并不适合。因此本文采用Pareto支配思想与外部档案集相结合的方式,对多个目标同时进行优化。考虑到粒子群算法收敛速度快,具有较强的全局寻优能力,且易于实现等优点,通过改进多目标粒子群算法求解模型,得到该多目标规划问题的Pareto前沿解集,进而根据不同的决策准则选择合适的配置方案。 2.1.1 缩放系数 粒子群算法需要以随机生成的方式初始化粒子种群,以此为起点搜索最优解,因此种群初始化解的质量将影响算法的收敛速度。目前比较常见的方法是丢弃不可行解,但是会造成内存浪费且效率较低。为使得生成的初始解集在可行域范围内,本文使用一种带约束的初始解生成方法[25]。假定在搜索空间S中,粒子Xi为满足某些约束条件,第d维的范围无法确定,只能确定最大范围为[lbd,ubd],此时随机产生的种群xi∉S,因此引入缩放系数μ(0<μ<1),对种群xi按照式(13)进行重置: (13) 其中基准变量bd定义为: (14) 在本文模型中,种群中每个个体Xi的m×n维矩阵代表一种可能的配置方案,由公式(7)至(12)得到矩阵中维度Pij随机取值的最大范围,即: ∀i∈I,j∈J,0≤Pij≤min(Mi,dj) (15) 2.1.2 约束处理方法 多目标优化问题的约束处理方法有很多种,其中比较普遍的是罚函数法[26]、丢弃不可行解、以及定义带约束的Pareto支配关系[13]等。由于罚函数法会增加计算的复杂度,不利于模型的求解。而丢弃不可行解又会造成一定的资源浪费。因此本文采用设定违反约束检查函数[27]的约束处理方法将生成的解空间约束在可行域内。针对模型约束(7)和(8),违反约束检查函数的公式为: (16) 当生成一个随机解的约束检查函数V>0时,表明该随机解违反了一个或多个约束条件,不在可行域内。当且仅当V≤0时,所有约束条件均得到满足,随机生成了一个可行解。 2.1.3 速度与位置的更新 模型中粒子搜索空间为m×n维,粒子Ni的位置和速度分别为m×n维向量矩阵形式: 根据个体最优和全局最优更新当前速度与位置,更新公式为: (17) (18) 其中c1和c2为分别为个体与群体的认知加速常数,用于平衡全局搜索与局部探索之间的能力。ω为惯性系数,目前使用较多的是动态调整惯性权重线性递减,优化粒子群迭代初期全局搜索性能和后期的快速收敛,同时保证了种群的多样性。惯性系数迭代公式为: ω=ωmax-(ωmax-ωmin)×iter/maxCycle (19) iter为迭代次数,maxCycle为最大迭代次数。 2.1.4 外部档案的更新 多目标优化问题的Pareto前沿解集是由所有非支配解所构成。支配关系是指假设给定两个可行解x和x′,则xPareto支配x′需要满足的条件为: ∀i∈I,fi(x)≥fi(x′) (20) ∃j∈J,fj(x)>fj(x′) (21) 本文采用外部档案存储前沿解集,当粒子种群完成一次迭代得到全局最优解后将追加到外部档案中,并根据拥挤距离机制保留有限个非支配解来维护外部档案。拥挤距离用来衡量外部档案中个体之间的密集程度,并将相似解舍弃,使得解空间分散。计算个体之间拥挤距离采用欧式距离公式: (22) 其中X,Y,Z分别表示三个目标函数值,并将其进行降序排列。 由以上相关设计得到算法的具体实施步骤如下: Step1设置各项参数,包括粒子群总数NP、迭代累计次数iter、最大迭代次数maxIter、惯性系数和加速度常数因子等。 Step2按照约束规则初始化粒子群所有个体的位置和速度,以及个体最优和全局最优位置;计算种群适应度值。 Step3将所有个体的适应度值进行快速支配排序,生成初始外部档案。 Step4更新惯性系数ω和所有粒子的速度与位置,并约束粒子的位置于可行域内;调整个体最优位置pBest。 Step5对所有粒子进行快速非支配排序,更新外部档案,计算拥挤距离维护非支配解集。 Step6根据拥挤距离降序排列外部档案,在前10个非支配解中随机选择一个,更新全局最优位置。 Step7iter=iter+1,如果iter<=maxCycle,转到step4;否则算法结束,获得外部档案Pareto解集。 该算法的流程图如图5所示。 图5 多目标粒子群算法(MOPSO)流程图 表1 运输时间矩阵表(/0.1h) 模型运行的硬件环境为Intel(R)Core(TM)i5-3570/3.4GHz/4GB RAM,软件环境为Winodows7操作系统,Matlab R2014a编程软件。设置粒子群算法的参数如下:粒子群总数NP=80,算法迭代次数maxIter=500,惯性系数ωmax=1,ωmin=0.1,加速度常数c1=c2=0.8。 缩放系数影响算法初始化的速度,将以上参数代入到算法的初始化中,得到生成初始解的时间随缩放系数的变化曲线,如图6所示: 图6 生成初始解时间随缩放系数变化曲线 可知,缩放系数μ=0.61时算法生成初始解的速度最快,平均用时2.5153s。 将上述参数数据代入到模型和算法中,经500次迭代,外部档案集解个数随迭代次数变化曲线如图7所示,得到该模型最终的Pareto前沿解集如图8所示: 图7 外部档案集解个数随迭代次数变化曲线图 图8 Pareto前沿解集 由于目标一为离散函数,因此在该维度上解集离散。三个目标之间不存在相互的支配关系,每一种都可以作为该模型最终的资源再配置方案,可以任选其一。本文采用专家意见法,由专家对三个目标的决策权重如p=(0.6,0.3,0.1)得到最终再配置方案如表2所示。 不同受灾情况的各灾害点,资源再配置方案也大不相同。表2中应急资源再配置方案为:原生灾害点1分别向此次生灾害点1、5共享14.1766个单位、2.6188个单位的资源;原生灾害点2向次生灾害点2共享13个单位的资源;原生灾害点3向次生灾害点3共享4.3900个单位的资源;原生灾害点4向次生灾害点4共享1.3168个单位的资源。 表2 数值实验结果 现有应急资源配置模型大多认为供应点可以毫无保留的全力支持灾害点的救援工作,而本文以原生灾害点为供应点,在基于区域互救和后续共享原则的情况下,灾害点本身资源有限,且灾区的整个救援工作还未结束,将其作为临时资源供应点势必要考虑原生灾害点灾民的心理因素从而对共享资源有所保留,不能全力支持其他区域。因此在考虑原生灾害灾民不满情绪的情况下,原生灾害点将会减少对应急资源的共享量。对比表3应急资源配置方案,与未考虑供应点的心理因素相比,本文考虑到原生灾害点灾民心理因素使得供应应急资源整体的共享比例减少了34.47%。由表4计算该配置方案下原生灾害点需求感知满意度为-2.25个单位。满意度同比提升了13.2361个单位。在以感知满意度为主要目标,且原生灾害点只作为次生灾害点临时资源供应方的情形下,这种供应资源共享的减少带来了原生灾害点由不满意到满意的变化是值得的。 表3 考虑与不考虑原生灾害灾民心理因素的配置方案对比 表4 两种配置方案的目标函数对比 在本算例的求解过程中,采用丢弃不可行解的方式超过了2小时仍未产生满足约束条件的初始解,而本文在标准多目标粒子群算法(MOPSO)中引入了缩放系数以及违反约束检查函数来改进粒子种群的初始化,方法运行10次,平均用时2.5153s就随机生成了满足约束条件的初始可行解及其目标函数值,验证了算法在解决该类问题的可行性。最后为了验证该算法对所建模型的高效性,本文与人工蜂群算法进行了对比实验。人工蜂群算法(ABC)是由Karaboga[28]提出的一种仿生群体智能算法,通过模拟蜜蜂采蜜行为寻找最优蜜源。对于多目标优化问题,比较常见的性能评价方法有:世代距离(GD)、空间度量指标(SP)误差比(ER)等[27]。本文采用世代距离(GD)来度量,公式为: (22) 其中,di表示第i个非支配解与真实Pareto前沿之间的最短距离,n为非支配解的数量。 设置相同的参数,分别对两种算法进行10次实验,取各自Pareto解集的并集得到相对应的Pareto最优前沿解集,如图9所示,改进的MOPSO算法在解空间中Pareto前沿面较ABC算法延展性更好,分布更为均匀,求得的解也更为丰富。由于该模型的真实Pareto前沿解集无法获取,本文把两组Pareto解集进行合并,将并集作为最终的真实Pareto前沿解集对两个算法进行性能对比分析。 将得到的实验结果代入公式(22)得到GD值。如表5所示,相较于人工蜂群算法而言,改进的多目标粒子群算法在本文模型的求解上更具高效性。 图9 改进的MOPSO与ABC的Pareto前沿解集对比 表5 两类算法GD值对比 原生灾害和次生灾害在时间上的前后序关系增加了情景结构上的复杂性,属于应急资源调度领域的关键问题之一。本文基于区域互救和后续共享原则,将供需双方灾民感知满意度刻画的不同引入到了存在次生灾害的联动应急资源配置当中,通过紧急共享原生灾害点部分应急资源来第一时间响应次生灾害,为解决存在次生灾害的应急资源配置问题提供了一个新的思路。模型以最大化各个受灾点灾民感知满意度,最大化单位时间运输量为目标,在多目标粒子群算法初始化阶段引入缩放系数和违反约束检查函数加快了解的生成,使用算例进行了仿真实验和对比分析,得到可根据决策者偏好进行选择的再配置方案。最后对是否考虑供方灾民心理做了对比实验,结果表明,相比于物资储备中心,本文模型中资源整体供应比例有所缩减,但原生灾害点灾民满意度提升明显,这种区域互救措施是行之有效的。由于灾害链中各个情景复杂多变,本文尚未考虑在多个不同情景下应急资源调度的差异、道路选择优化问题,以及应急资源多种类下存在的资源替代关系对灾民感知满意度带来的变化,这也是之后需要进一步深入研究的问题。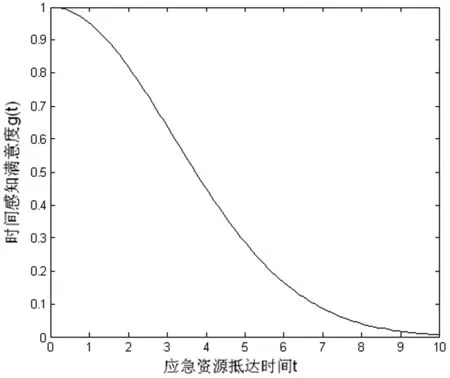
1.3 模型建立
2 改进的多目标粒子群算法
2.1 算法设计


2.2 算法步骤

3 算例分析
3.1 参数设计


3.2 实验结果

3.3 算法性能检验

4 结论
