描述逻辑ALC中关于伪子概念极小改变的R-演算∗

王雨晖，眭跃飞

1(中国科学院 计算技术研究所 智能信息处理重点实验室，北京 100190)

2(中国科学院大学 计算机与控制学院，北京 100049)

3(中国再保险(集团)股份有限公司 信息技术中心，北京 100033)

信念修正是接受一个新信念和更新我们已有信念的过程，它的发展是哲学以及后来的计算机科学所需要的.在计算机科学中，为了更新数据库，Doyle[1]提出了保真系统(truth maintenance systems)，自此，信念修正成为人工智能中的一个重要分支；而在哲学中，信念逻辑中的逻辑研究也需要考虑人类信念是如何更新和修正的.

由Alchourrón，Gärdenfors和Makinson[2−4]提出的AGM公设是一个修正算子应该满足的基本条件集合，它是用公式A去修正理论K，使得如果K◦A⇒K′，则K′是K∪{A}的极大协调子集.

李未[5]给出了基于一阶逻辑[6]的Gentzen-型推导系统R-演算，用来将R-构型(configuration)Δ|Γ归约到协调理论Δ∪Θ.Δ∪Θ是Δ∪Γ的极大协调子集，其中，Γ是协调公式集合，而Δ是协调的原子或原子公式否定的集合.在这里，Δ|Γ相当于迭代修正Γ◦Δ.因此，推导系统给出了具体的修正算子，并且证明是满足AGM公设的.

对于描述逻辑ALC，存在这样的 R-演算 SDL[7]:其中 R-构型Δ|Γ可以被归约为理论Δ∪Θ(记为)，当且仅当Θ是Γ关于Δ的一个集合包含极小改变(⊆-极小改变)(记为).这里，Θ是Γ的子理论，并且它与Δ是极大的、协调的(maximal consistent)(不是极大协调的(maximally consistent))，即:对任何理论Ξ满足Θ⊂Ξ⊆Γ，Ξ与Δ是不协调的.在这里，我们用Δ，Θ来表示Δ∪Θ.因此，R-演算SDL关于⊆-极小改变是可靠的和完备的.

⊆-极小改变[8−10]是关于集合包含关系的，即:如果Δ|Γ⇒Δ，Θ在R-演算中是可证的，则Θ是Γ关于Δ的一个极小改变，如果对于任意的公式A∈Γ，Θ∪Δ⊬A都蕴含有Θ∪Δ├¬A.因此，我们称Θ是Γ关于Δ的⊆-极大协调子集.

针对⊆-极小改变和R-演算SDL，我们来看具体的例子.已知Tony是一位男生，性格开朗，四肢健全，即:在我们的知识库当中，存在着这样一条断言(HavingarmsHavinglegs)(Tony).然而一次突发的事故让Tony失去了双腿，也使得关于Tony产生了一条新的事实断言¬Havinglegs(Tony).因此，我们就需要对于原有知识库中的断言做出修正.而按照之前R-演算SDL当中的修正规则，我们将得到如下修正:

可以看到，经过修正后的知识库中将只剩下断言¬Havinglegs(Tony)，即Tony依然是有胳膊的断言没有了，这当然不是我们想要的.直观地，我们应当获得这样的修正:

显然，SDL中的规则是会删除掉Γ中过多的有效信息的.

因此在本文中，我们将考虑另一种极小改变的定义:

而公式A是另一个公式B的伪子公式(pseudo-subformula ofB)，如果删除B中某些子公式可以得到A.

在描述逻辑中，我们也有类似地对于极小改变的定义[11].在描述逻辑中，我们有概念的次子概念(parasubconcepts)和伪子概念(pseudo-subconcepts)，对应于子公式和伪子公式，并且基于此，我们给出关于-极小改变可靠和完备的R-演算TDL.需要注意的是，这里的极小改变并不是关于描述逻辑中的断言，而是关于概念的.比如，概念集合X是概念集合Y关于概念集合Z的一个-极小改变.具体地，我们定义:

概念C是另一个概念D的伪子概念，如果通过删除D中若干个原子概念符号可以得到C.

显然，新的极小改变将使我们在修正的过程中，可以将修正的最小单元降到原子概念级，可以做到在修正的过程中只剔除掉那些与新事实产生矛盾的原子概念，从而可以最大限度地保留原有断言中的有效信息.

相应地，我们也将给出如下的R-演算:

R-构型Δ|Γ在R-演算TDL中可以被归约为理论Δ∪Θ(记为即Δ|Γ⇒Δ，Θ在Gentzen型推导系统TDL中是可证的)，当且仅当Θ是Γ关于Δ的-极小改变(记作).这是对于TDL的可靠性定理和完备性定理.

作为结果，对于上面的修正，我们在TDL将会获得如下修正:

本文第1节给出描述逻辑ALC的基本定义，并且定义了简化的ALC的逻辑语言和语义.第2节定义了极小改变及其相关概念和命题.第3节给出了关于断言C(a)的R-演算，并证明了对于Δ|C(a)的推导规则是可靠和完备的.第4节给出了关于理论的R-演算TDL(对于断言集合Γ的推导规则集合)，使得推导规则集合是关于极小改变可靠和完备的.最后总结全文并提出下一步工作设想.

1 预备知识

1.1 描述逻辑ALC

描述逻辑ALC由下列的逻辑语言、语法和语义组成.

描述逻辑ALC的逻辑语言包括下列符号.

· (个体)常量符号:c0，c1，…；

· 原子概念符号:A0，A1，…；

· 角色符号:R0，R1，…；

· 辅助(auxiliary)符号:(，).

概念定义为

原始断言定义为

其中，R(c，d)和A(c)被称为原子的.

模型M是一个序对(U，I)，其中，U是非空集合(M的论域)，并且I是一个解释，使得:

· 对任何常量符号c，I(c)∈U；

· 对任何原子概念符号A，I(A)⊆U；

· 对任何角色R，I(R)⊆U2.

概念C的解释CI是U的一个子集，使得:

在语法中，我们使用¬，∧，→，∀，∃来表示逻辑联结词和量词；而在语义中，我们用～，&，⇒，A，E去表示相应的联结词和量词.

断言φ在M中是满足的，记为M⊧φ或者I⊧φ，如果:

1.2 伪子公式和-极小改变

1.3 伪子概念和-极小改变

2 关于单个断言的R-演算TDL

3.1 R-演算TDL

一个断言集合Γ的R-演算TDL:

3.2 实 例

首先来看本文开篇的那个例子.

4 总结与展望

本文给出了描述逻辑ALC中关于伪子概念()极小改变的R-演算TDL，解决了修正过程中误删有效信息的问题，使得在修正的过程中可以保留下尽可能多的有效信息.但修正过程中是否存在信息冗余的问题呢?

对于断言((birdcanfly)(mammalcanwalk))(a)，其中，bird(a):a是鸟，mammal(a):a是哺乳动物，canfly(a):a会飞，canwalk(a):a会走.当出现新的断言{¬bird(a)，¬canwalk(a)}时，我们将有如下修正:

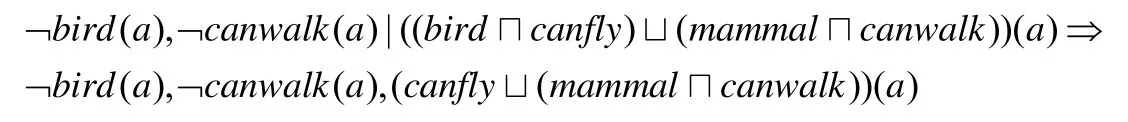
显然，这是等价于¬bird(a)，¬canwalk(a)，(canflymammal)(a)的.

同样地，在TDL中，我们还会有这样的推导:

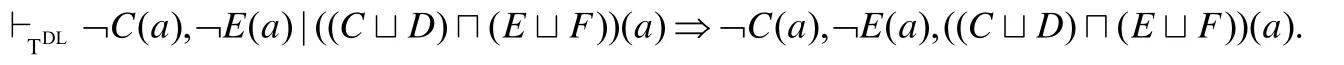
此外，为了获得更好的表达能力，描述逻辑在ALC的基础上，通过进一步增加构造子的方式还得到了一些重要的扩展.因此，我们下一步还将考虑扩展R-演算到包含数量限制(≥nR和≤nR)的描述逻辑ALCN和带有角色构造子的描述逻辑ALCR中，分别针对数量限制和角色构造子给出修正规则.而由于ALC中都是原子角色，即没有角色的否定形式，因而在ALC中对量词∀R.C和∃R.C进行修正时，并不考虑角色R在其中的作用.但是在引入了角色构造子之后，角色也有了它的补、交、并的形式，因此，我们在给出ALCR中对于角色构造子修正规则的同时，也需要注意原先对于量词的修正规则同样需要修改.