A linear ADRC-based robust high-dynamic doubleloop servo system for aircraft electro-mechanical actuators
2019-10-26ChunqiangLIUGuangzhaoLUOZheCHENWencongTUCaiQIU
Chunqiang LIU, Guangzhao LUO, Zhe CHEN, Wencong TU, Cai QIU
School of Automation, Shaanxi Key Laboratory of Small & Special Electrical Machine and Drive Technology,Northwestern Polytechnical University, Xi'an 710129, China
KEYWORDS Active Disturbance Rejection Control (ADRC);Disturbance observer;Electromechanical actuators;Servo control
Abstract Compared with traditional hydraulic actuators,an Electro-Mechanical Actuator(EMA)is small in size and light in weight,so it has become more widely used.Aerodynamic load on aircraft control surface varies dramatically, and a change of flight environment leads to uncertainties of motor parameters. Therefore, high-dynamic response and strong anti-disturbance capability of an EMA are of great significance for aircraft rudder control and flight attitude adjustment.In order to improve dynamic response and disturbance rejection of an EMA and simplify control parameters tuning,a robust high-dynamic servo system based on Linear Active Disturbance Rejection Control(LADRC)is proposed for an EMA employing a Permanent Magnet Synchronous Motor(PMSM).Firstly, total disturbances of the EMA are analyzed, including parameter uncertainties, load variation,and static friction.A disturbance observer based on a reduced-order Extended State Observer(ESO)is designed to improve the anti-interference ability and dynamic performance. Secondly,the servo control architecture is simplified to a double-loop system,and a composite control of position and speed with acceleration feed-forward is presented to improve the EMA frequency bandwidth.Thirdly,the ideal model of the EMA is transformed into a simple cascade integral form with a disturbance observer,which makes it convenient to analyze and design the controller.Robustness performance comparisons are realized in frequency domain. Finally, simulation and experimental results have verified the effectiveness of the proposed strategy for EMAs.
1. Introduction
With the development of more-electric aircraft, an important feature is that a large number of hydraulic systems are replaced by electric drives or Electro-Hydrostatic Actuators (EHAs)1-4A great number of research reports on Electro-Mechanical Actuators (EMAs) have been carried out5,6The use of EMAs greatly reduces airborne hydraulic components and pipelines,and the weight of an aircraft. An EMA is used in the miboard spoiler in Boeing 787,and the horizontal stabilizer actuators in Airbus 350 and 380 are EMAs. In the future, EMAs will also be used for landing gears, aircraft doors, elevators,and other operations. In recent years, the Permanent Magnet Synchronous Motor (PMSM) has been widely used in EMA servo systems because of its high torque-to-current ratio and high efficiency. With higher requirements of fast positioning and simple debugging, we have to overcome more challenges:(A) improve the frequency bandwidth of the position closed loop; (B) improve the ability to suppress load torque disturbance and parameter perturbations;(C)the parameters tuning method should be simple and suitable for engineering.
In combat aircraft, high maneuverability is required to ensure mission completion and aircraft safety, which puts forward higher requirements for the frequency response of EMA servo control. The cascade three-closed-loop servo system(including a position loop, a speed loop, and a current loop)is widely used in EMAs2In general, the bandwidth of a cascade control system decreases from the inner loop to the outer loop, and the outer-loop bandwidth is 1/5-1/10 of the innerloop bandwidth, so the bandwidth of the three-closed-loop system is limited.In order to improve the frequency bandwidth of the servo system, the three-closed-loop system should be simplified. A double-loop servo system based on nonlinear active disturbance rejection control is proposed,and good control results are obtained,7but it is difficult to tune parameters for a nonlinear controller. Therefore, it is necessary to further improve the control architecture to realize high-dynamic response without resorting to complex nonlinear functions.
In addition to the fast response to position instruction,suppressing load disturbance is another key technology to improve the EMA performance. The aircraft EMA servo system is a strong nonlinear system with unavoidable and unmeasured disturbances and parameter variations8Moreover, due to the influences of strong airflow and other uncertain factors during a flight, the load of the aircraft rudder could change dramatically.Thus,a strong load disturbance suppression ability is required for the control of an EMA. With traditional control technologies, such as PID, it is difficult to achieve a satisfactory performance. A number of control methods have been proposed, such as artificial neural networks,9-11sliding mode control,12,13robust control,14,15and internal model control.16,17These algorithms still require a motor model,but disturbances and uncertainties widely exist in EMA servo systems, which have adverse effects on control performance and even bring the instability of control systems.
An adaptive internal model control scheme for PMSM speed servo systems is presented in Ref.9.For the case of large variations of load inertia,an inertia identification algorithm is adopted to improve the performance of internal model control.A model-based control method combined with on-line identification increases the complexity of control systems.In order to further reduce the model dependence of a controller,constructive methods can be adopted, such as Active Disturbance Rejection Control (ADRC), which was proposed by Han18
ADRC is not predicated on an accurate and detailed dynamic model of a plant, and is extremely tolerant to uncertainties.ADRC has attracted attention and application in motion control and EMAs19-21ADRC was used for hydraulic servo systems,and high-gain feedback was avoided.22In Ref.23, an ADRC method with a reduced-order extended state observer for a PMSM in Computer Numerical Control (CNC) machining was proposed and achieved high accuracy in simulation results.In Ref.24,a modified ADRC was designed,and the disturbance rejection property was independent of the speed loop control coefficient.Meanwhile,ADRC has beenapplied tothe flightcontrol of various spacecraft25Therefore,the inherent robustness of ADRC is very suitable for aviation EMAs.
For external load disturbance, various methods have been used to estimate the load torque, such as a model-based load torque observer.26However,the model-based observer method is vulnerable to parametric variation,such as inertia.A nonlinear ESO was used to estimate the load torque for a PMSM speed regulation system in Ref.16,and a high-order fast terminal sliding-mode load torque observer was designed in Ref.27.However, the parameters of nonlinear load observers, nonlinear ESOs, and nonlinear control laws are difficult to tune.Optimization methods are often adopted to adjust the control parameters.28,29A scaling and bandwidth parameterizationbased parameter tuning method was shown in Ref.30for Linear ADRC (LADRC). It makes parameter tuning easier than nonlinear ADRC, so LADRC is beneficial to engineering applications31and is utilized in this paper.
This paper proposes a new robust high-dynamic doubleloop servo system based on LADRC for EMAs. The traditional cascade structure of position and speed loops is changed to a parallel structure as the outer loop,and the current loop is the inner loop to control the PMSM torque. A robust highdynamic servo control scheme and a reduced-order Linear ESO(LESO)based on speed information are presented in Section 3.In order to improve the system bandwidth,a composite control law of position and speed with a tracking differentiator is proposed in Section 4. A compensation method with total disturbances information is presented. The proposed method based on LADRC considers parameter uncertainties and unknown external disturbances. Moreover, frequency responses of loop gain and disturbance rejection are analyzed.In Sections 5 and 6, the validity of the proposed control algorithm is confirmed by simulation and experiment.
2. Dynamic model and disturbances of EMA servo system
2.1. Principle architecture of EMA
A reentry EMA for aircraft and the principle control block diagram of the EMA servo driver are shown in Fig. 1. When the servo PMSM rotates, the screw or nut is driven to rotate by a gear reducer,and the nut or screw rod translates the rotational motion into a linear motion through the linear limiting mechanism. The desired aircraft rudder angle is achieved by controlling the PMSM. The PMSM servo driver system is a key component, and seriously affects the control performance of the EMA.As a result,it is regarded as the research focus.In Fig.1,θrefis the given position reference,θ is the position feedback information,ωris the electric angular velocity,ia,ib,and icare the PMSM stator currents,iαand iβare the currents after Clarke transformation, idand iqare the d axis and q axis currents,respectively,andare the d axis and q axis current references,respectively,andare the d axis and q axis voltage references, respectively, andandare the voltage references after inverse Park transformation for PWM generation,respectively.
The whole servo driver includes a PMSM, an inverter, and a control unit. The inner loop current controller aims to control the torque,and the proposed position and speed controller based on LADRC is the outer loop. The output of the proposed controller is the input reference of the iqcurrent loop,and the d axis current reference=0. The position feedback information θ is obtained by a resolver mounted on the PMSM.
2.2. Model and disturbance analysis of EMA
Firstly,the dynamic model of the EMA system is analyzed.In the dq rotor reference frame of the PMSM, when the control method of id=0 is adopted,the surface-mounted PMSM electromagnetic torque Tecan be expressed as
where pnis the number of pole pairs;Ld,Lqare the d axis and q axis stator inductances,and Ld=Lq;id,iqare the d axis and q axis currents; ψris the flux linkage.
The speed dynamic equation can be expressed as
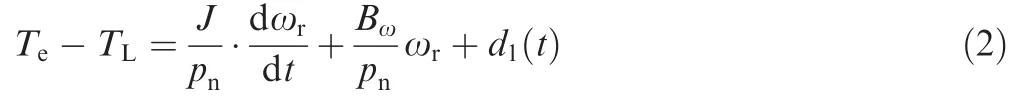
where TLis the load torque, J is the moment of inertia, ωris the electric angular velocity, Bωis the viscous friction coefficient,and d1(t)is other unmodeled and unknown disturbances.
Combining Eqs. (1) and (2), the position and speed dynamic equation of the PMSM servo system is depicted as

If the viscous friction-Bωωr/J and the tracking error of the q axis current iqare treated as disturbances, Eq. (3) can be deduced as

It is well known that various disturbances exist in an aircraft EMA, e.g., inertia variation, load torque variation, and nonlinear friction of gears and screws. The aerodynamic load is small when a plane flies flat at low speed, but the angle of attack is small and the load is large when the plane flies flat at high speed. When using model-based control strategies,the control performance of an EMA servo driver is affected by parameters variations and aerodynamic load during aircraft flight,so a robust method is proposed in next section,which is insensitive to load torque disturbance.
3. Reduced-order ESO-based disturbance observer for EMA servo system
3.1. LADRC-based high-dynamic control scheme
In order to improve instruction rapidity and the ability of load disturbance rejection,a high-dynamic control scheme based on LADRC for the EMA is shown in Fig.2.When the rudder surface is in different positions, the inertia J converted to the motor shaft will change. In addition to parameters perturbation, load torque, and unmodeled uncertainties, the nonlinear characteristics of the EMA are considered as disturbances,such as static friction.
A practical way to implement this high-dynamic LADRC controller is given below:

Fig. 2 High-dynamic control scheme based on LADRC for EMA.
(1) A mathematical model is established to analyze the disturbances in the EMA, as shown in Eq. (4).
(2) An LESO-based disturbance observer is constructed,and an approximate ideal model is acquired after disturbance compensation.
(3) A position and speed feedback control law with the approximate ideal model is designed.
3.2. Reduced-order linear disturbance observer based on speed information
For a second-order servo system, a third-order ESO is usually designed to estimate disturbances. However, according to Eq. (4), when the speed ωris measurable, disturbances d(t)can be estimated by speed and current information, so the position information is not necessary. A reduced-order ESObased disturbance observer decreases the computational complexity of the algorithm, and improves the rapidity of perturbation estimation.
According to Eq. (4), a reduced-order ESO-based disturbance observer using the measured speed ωris designed as

where ^x1=[^ωr, ^d(t)]T, B2=[^b, 0]T, C=[1, 0], ^b is the estimate of the control gain b, ^ωris the estimate of the electrical angular velocity ωr, ^d(t) is the estimate of the lumped disturbances d(t), L=[l1, l2]Tis the observer gain matrix, and l1and l2are observer parameters to be designed.
Define x1=[ωrd(t)]T,the estimation error is x~1= x1-^x1,and the following error dynamics is obtained, which is independent on the feedback control law:


Find the matrix L to meet this requirement. It can be accomplished if the observability matrix P has full rank. For system Eq. (6), P=[C,CA1], and rank(P)=2, so the system is completely observable. We can find that if l1and l2are positive values,the disturbance estimation error is Bounded Input Bounded Output (BIBO) stable.
The transfer function matrix of the observer is as follows:

where P(s)=s2+l1s+l2, M(s)=l2, and N(s)= ^bl2.
The characteristic equation of Eq. (7) can be deduced as s2+l1s+l2=0. If the roots of the characteristic equation are set as double roots as ωo, then parameters can be selected as l1=2ωoand l2=ω2o. It shows that only one parameter needs to be adjusted in the reduced-order ESO-based disturbance observer. It is very beneficial to engineering implementation.
The bandwidth of LESO ωoplays an important role in the anti-interference performance of the EMA system. The larger the ωo, the higher the bandwidth, and the more parametric uncertainties or disturbances in the EMA system can be tolerated. However, it is constrained by other factors, which are listed below.
(1) Expected bandwidth of the position closed-loop system ωe. According to Ref.30, in order to satisfy the antidisturbance performance, an appropriate minimum is ωo=5ωe-10ωe.
(2) Measurement noises. In the servo drive system, highvoltage power devices switch frequently, which may interfere with current sampling and low-voltage analog circuits.Measurement noises appear in the sample channel. This limits the enhancement of the bandwidth.
(3) Resolution of the position feedback sensor. A high bandwidth is not suitable for the EMA servo system with a low-resolution position sensor. Because a high bandwidth is more sensitive to the quantization error,which will cause high-frequency oscillations in the observed disturbances. When a high-resolution sensor is used, the bandwidth can be appropriately increased.
(4) Discretization period.Digital discretization implementation of LESO also has a great impact on the choice of the bandwidth. The shorter the discretization period,the larger bandwidth can be selected.
Therefore,the choice of either upper or lower of the LESO bandwidth ωois a compromise that requires a balance between various constraints.
4. Robust composite control based on LADRC
In this section,a composite control law is designed.The linear control law is considered for the EMA servo system to facilitate implementation in practice. In order to improve the frequency bandwidth, the three-closed-loop system is simplified into a double-loop system. The basic form of the controller is designed to realize a composite control of position and speed. Then, a control law based on LADRC is proposed.
4.1. Basic double-loop servo control strategy
For the servo system Eq.(4),a double-loop control scheme for the EMA is presented in Fig.3 to improve the frequency bandwidth. In Fig. 3, kp1is the speed feed-forward coefficient, and θ*is the position target value. In order to realize a composite control of position and speed, a linear control law composed of position and speed tracking errors is designed as

where e=[eθ,eωr]T, K1=[k11, k12], and k11, k12, and k13are positive numbers.
Consider a candidate Lyapunov function as(eθ,eωr) can be deduced as

Combining Eqs. (4) and (8),=0 for a constant θ*, and


The open-loop transfer function of the speed loop Gωopand the closed-loop transfer function Gωclare respectively

Letting bk13=and bk12=2ξωn, the parameters are obtained as the following, which are utilized in simulation and experiment:

where ξ is the damping ratio, and ωnis the desired frequency.
4.2. Improving position command response using tracking differentiator
In the EMA servo system, a fast dynamic performance is required.Thus,if the position command is a step signal,overshoot appears inevitably, which is not allowed in many applications.At the same time,the position reference in the EMA is not fixed, but varies with time. In order to improve the position tracking performance of the dynamic position reference,acceleration feed-forward using a Tracking Differentiator(TD)is introduced.A linear tracking differentiator is designed in this paper. The desired position and speed transient profile and acceleration information are obtained by solving the following discretized equations with the Euler discretization method:

where f is an intermediate variable for calculating the acceleration a*(k), θrefis the given position reference, θ*is the actual position target value for closed-loop control,is the desired electric angular velocity, a*is the angular acceleration, labels k-1 and k represent the previous time and current time,respectively, T1is the discretization period in a microprocessor, and r is the differentiator parameter.
The tracking differentiator realizes fast tracking of θrefand provides the desired speed and acceleration information. The larger parameter r,the faster θ*tracks the given reference θref.When the steady state is reached,θ*is equal to θref.Note that,depending on the physical limitations in each application,parameter r can be selected according to desirable specifications.


Fig. 3 Basic composite control architecture for EMA.

where Mag_TD is the magnitude characteristic, Phase_TD is the phase characteristic, and ω is the frequency.
A control block diagram with acceleration feed-forward is shown in Fig. 4. A composite controller with acceleration feed-forward using the TD is designed as

where kp2is the acceleration feed-forward coefficient, and ^b is the estimate of b in Eq. (4).
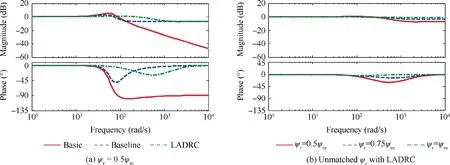
With the tracking differentiator, the desired speed ω*r and acceleration a*are acquired. A high-dynamic response to instructions is achieved by feedforward withand a*,instead of relying entirely on a closed-loop adjustment of position and speed errors.The strength of the feedforward effect is changed by adjusting kp1and kp2. Usually, 0 In Eq.(16),it is assumed that the disturbance observer can accurately estimate total disturbances, ^d(t)≈d(t), so an approximate ideal model can be acquired, ˙x = A1x+Bu0. It is a cascade integral form system. In theory, in the presence of disturbances, there is no need to introduce an integrator into the feedback control law to eliminate the state steady error. The reduced-order ESO-based disturbance observer compensates for the uncertainties and disturbances of the servo system. Therefore, according to Fig. 2, a high-dynamic composite controller is designed as in Eq. (17), and the proposed LADRC-based control scheme for the EMA is shown in Fig. 5.where e=[eθ,eωr]T, K2=[k21, k22], in which k21and k22are positive numbers, θ*is the estimate of b in Eq. (4), and ^d is the estimate of time-varying disturbances d(t). Finally, the pole placement design technique selecting the feedback matrix K2is given. The error dynamic equation can be written as The characteristic equation associated with Eq. (18) is det(λI-A2)=0, and the desired characteristic roots are λ1=λ2=ωe; therefore, K2can be selected as K2=[/b,2ωe/b]. Fig. 5 High-dynamic control architecture based on LADRC for EMA. To analyze the performance of the proposed robust highdynamic double-loop servo system, position loop gain frequency response and disturbance rejection are analyzed in this section. Because the proposed closed-loop system is linear,classical control tools are used to investigate its control properties. For more convenient comparison, different control methods are abbreviated as follows: (1) Basic: the basic double-loop servo control strategy. (2) Baseline: double-loop servo control with acceleration feed-forward using the TD. (3) LADRC: composite control law based on LADRC. According to Figs.3-5,transfer functions between the output position θ and the position reference θ*as well as d(t) to each of the output θ(s) are computed and summarized in Table 1.where P(s)=s2+l1s+l2,M(s)=l2,and N(s)= ^bl2. According to the deduced transfer functions, a frequency response analysis will proceed. A prototype PMSM is tested with the nominal parameters shown in Table 2,and the PMSM is utilized in simulation and experiment. The parameters for the Basic controller are: ξ=0.707,ωn=20π, kp1=1, k11=10, k12=2ξωn/bn, k13=/bn,and bn=1.5ψrn/Jn. Bode plots of the position loop gain transfer function θ(s)/θ*(s) with different controllers are shown in Fig. 6. The control strategies with acceleration feed-forward (Baseline and LADRC)have higher magnitudes and lower phase delays in the high-frequency range than those of the Basic controller.Therefore,acceleration feed-forward makes the response to the position command faster. Bode plots of θ(s)/θ*(s) with unmatched parameters are shown in Fig. 7. Compared with the matched parameter, the magnitude of the high-frequency range is slightly attenuated.The reason is that ^b=10b is not matched with b,so the acceleration feed-forward compensation becomes weaker. Meanwhile, it shows that the LADRC controller has a higher bandwidth than that of the Baseline controller when the moment of inertia mismatches. With the LADRC controller,Bode plots of unmatched J are shown in Fig. 7(b), with J=Jn, 5Jn, 10Jn(Jnis the normal moment of inertia). WhenJ=10Jn, the characteristics of the low-frequency section are not affected, and the amplitude of the high-frequency band is attenuated, but the bandwidth is still larger than that of the Baseline controller without disturbance compensation.The EMA's ability to suppress inertia variation disturbances is improved. Table 2 Parameters of the tested PMSM. Bode plots of the position loop gain transfer function are shown in Fig.8(a),with ψr=0.5ψrn(ψrnis the normal permanent flux linkage). The LADRC controller has a higher bandwidth than that of Baseline when the flux linkage ψrmismatches. With the LADRC controller, Bode plots of unmatched ψrare shown in Fig. 8(b), with ψr=0.5ψrn,0.75ψrn, ψrn. The magnitude of the high-frequency section is reduced by -7 dB, so the control performance is minimally affected by uncertainty of the flux linkage. An important performance of the EMA is the ability to suppress disturbances, such as load torque, so the frequency response of disturbance rejection is analyzed in this section. Fig. 6 Bode diagrams of transfer function θ(s)/θ*(s) with matched parameters. Table 1 Closed-loop transfer functions of different control architecture. Fig. 7 Robustness to inertia J. Fig. 8 Robustness to flux linkage ψr. Bode plots of the transfer function between the disturbances and the output position θ(s)/d(s) are shown in Fig. 9.It shows that the disturbance rejection performances of Basic and Baseline are identical. The reason is that the acceleration feed-forward technology does not change the transfer function θ(s)/d(s), as shown in Table 1. The magnitude with the LADRC controller is far smaller than those of Basic and Baseline. It means that the LADRC controller has a stronger ability to suppress disturbances. Bode plots of the transfer function θ(s)/d(s) with mismatched parameters are given in Fig. 10. In Fig. 10(a), with J=Jn, 5Jn, 10Jn, the magnitude characteristics of the lowfrequency section are increased by 20 dB when J=10Jn,while the amplitude of the high-frequency range is not affected. In Fig. 10(b), with ψr=0.5ψrn, 0.75ψrn, ψrn, compared with the Baseline controller (see Fig. 9), an excellent parameter perturbation rejection property is demonstrated, which is almost unaffected by ψrparametric uncertainties. The LADRC controller still has stronger disturbance rejection than that of Baseline even in the presence of significant uncertainties. For digital execution,the Euler method is used to discretize the proposed LADRC-based disturbance rejection algorithm.The position and speed sampling frequency is 5 kHz. The tracking differentiator is discretized as in Eq. (13), and the reducedorder ESO shown in Eq. (5) is implemented as Fig. 9 Comparison of disturbance suppression with matched parameters. Fig. 10 Disturbance rejection robustness with LADRC. where ^ωr(k-1) and ^ωr(k) are the previous-time and currentperiod estimates, respectively, ωr(k) is the current-time measurement, e(k) is the current observation error,(k-1) is the previous-time q axis current reference, θ*is the estimate of b in Eq. (4),(k-1) and(k) are the previous-time and current-time estimates,respectively,T1is the discretization period,and T1=0.0002 when the sampling frequency is 5 kHz. The composite control law shown in Eq. (17) is implemented as where θ*(k) and θ(k) are the current-time position reference and measurement,respectively,θerr(k)is the current-time position error,(k)and ωr(k)are the current-time speed reference and measurement, respectively, ωrerr(k) is the current-time speed error, a*(k) is the current-time angular acceleration for feed-forward,(k) is the current-time q axis current reference,and T1is the discretization period. To validate the effectiveness of the proposed servo control strategy based on LADRC, simulation results are presented in this section. The servo control performance is evaluated by the performance criterion, i.e., the integral of the absolute magnitude of the error, IAE, which is written as When a set-point command θref=200 rad, Fig. 11 shows the waveforms of different parameter r in the Tracking Differentiator (TD). It shows that the actual position reference θ*tracks the given command θreffaster when r=6. However,the current iqof r=6 is higher than that of r=4. Therefore,parameters r should be synthetically selected according to the dynamic response requirement,current limitation of the driver,and other factors. Fig. 11 Simulation results of different parameter r in tracking differentiator when θref=200 rad. When a set-point command θref=200 rad and J=2Jn,Fig. 12(a) shows the waveforms (θ*, θ,, ωr, θerr, ωrerr,d(t))of the position reference,position,speed reference,motor speed, position tracking error, speed tracking error, and observed total disturbances, respectively. The maximum position error θerris 0.63 rad with Basic, and it is 0.35 rad with Baseline, while it is 0.045 rad with LADRC, where disturbances are accurately estimated. A robustness analysis of setpoint tracking with parametric uncertainties is shown in Fig. 12(b), when J=Jn, 2Jn, 5Jn, 10Jnand ψr=0.5ψrn,0.75ψrn, ψrn. The IAE gradually increases with an increasing inertia J or a decreasing flux linkage ψrunder the Basic and Baseline controllers, but it is basically unchanged with LADRC. It means that LADRC has a stronger robustness to parametric uncertainties. When J=2Jnand the load torque abruptly varies,Fig. 13(a) shows responses of position and speed. At 3.0 s,the position drops to 199.76 rad, the setting time is about 180 ms, and a 0.2 rad steady state error exists with Baseline.However, the position is almost immune to load disturbances with LADRC. A robustness analysis of sudden load disturbance with parametric uncertainties is shown in Fig. 13(b).When the position command is constant, the acceleration α*from the TD is zero. Under the load disturbance, the IAEs of Basic and Baseline are identical. The simulation results are consistent with the theoretical analysis in Fig.9.Moreover,the IAE of LADRC is smaller than that of Baseline, so LADRC has a stronger robustness to serious disturbances including load variations and parametric uncertainties, which is consistent with the disturbance rejection frequency analysis. Fig. 12 Simulation results when θref=200 rad. Fig. 13 Simulation results with TL=5 N·m load variation. The position command is usually not a constant value in an aircraft EMA. As the rudder surface keeps oscillating, the position command is time-varying. In order to further verify the dynamic tracking performance,a sinusoidal position reference is implemented in the following simulation. Compared to a basic double-loop servo system, acceleration feed-forward is introduced in the Baseline method to accelerate responses to instructions. This method extracts acceleration information from instructions by a tracking differentiator, and does not depend on position and velocity errors.Fig.14(a)shows simulation results of the three methods with a sinusoidal reference θref=5sin(6πt)[1-exp(-15 t3)]rad. In the dynamic tracking process, the position error θerrand the speed error ωrerrare smaller with Baseline (acceleration feed-forward) than those of the Basic method (without acceleration feed-forward). With matched parameters (see Fig. 14(a)), Baseline and LADRC are close to each other. They both include acceleration feed-forward. θerris not more than 0.05 rad, and ωrerris not more than 0.8 rad/s. Under an unmatched inertia J(see Fig. 14(b)), the maximum θerris 0.49 rad with Basic,and it is 0.27 rad with Baseline, while it is still 0.05 rad with LADRC. Parameter perturbations are estimated by the disturbance observer and compensated, and the influences of the unmatched inertia J and the unmatched flux linkage ψrare very small, so a better robust performance is achieved, which is consistent with the loop gain frequency response analysis. A robustness analysis of parametric uncertainties with θref=5sin(6πt)[1-exp(-15 t3)] is shown in Fig. 15. The index IAE gradually increases with an increasing inertia J or a decreasing flux linkage ψrunder the Basic and Baseline controllers, but it is almost unaffected under LADRC. An EMA often works in a low-speed range after reaching a certain position. Unmodeled static friction is the main disturbance affecting tracking performance at low speed. In order to further verify the rejection to unmodeled nonlinear disturbances, a low-velocity trajectory is given as follows: θref=20sin(0.2πt) rad. In Fig. 16, the static friction of the machine is 0.8 N·m. Due to static friction, the speed is distorted at the zero crossing with Baseline,but it is smaller with LADRC.Therefore,even with low speed and static friction disturbance,an excellent robustness is achieved with LADRC. Experiments are conducted to verify the proposed servo control system in this section.The experimental platform is shown in Fig. 17. A TMS320F28335 DSP is used as the processor of the EMA driver system. Three-phase currents are measured using a hall current sensor. The switching frequency is 10 kHz. A resolver and a resolver-to-digital converter AD2S1200 are applied to measure the PMSM mechanical angle and speed. The disturbance rejection performances of Basic and Baseline are the same, as shown in Figs. 9 and 13,so the rejection performance to parametric perturbation is compared between Baseline and LADRC controllers in experiments. Fig.14 Simulation results of θref=5sin(6πt)[1-exp(-15 t3)]rad with different parameters. Fig. 15 Robustness analysis of parametric uncertainties with θref=5sin(6πt)[1-exp(-15 t3)]. Fig. 16 Tracking performance at low speed with unmodeled static friction. Fig. 17 Experimental platform. The EMA stays at a certain angle to maintain flight attitude,so set-point tracking is tested. Fig. 18 shows the responses of a step position reference θref=200 rad, and r=6 in the TD.The inertia change is simulated by connecting and disconnecting the loading motor and the PMSM. When the parameters are matched, the position error θerrdoes not exceed 0.2 rad, and the control effects of the two algorithms are similar.When J=2Jn,the maximum θerrwith Baseline is 0.6 rad,but θerrwith LADRC is 0.2 rad, which is smaller than that of Baseline during dynamic tracking. Moreover, the steady state is 0.08 rad with Baseline, but it is eliminated with LADRC.For the set-point tracking test,better steady and dynamic control effects are achieved with LADRC. Fig. 19 Experimental results of load disturbance. Fig.19 shows responses when the load torque abruptly varies.When a sudden load is added,the torque current iqrises to 6 A. With the Baseline controller, the position drops to 199.78 rad, and the steady state error is 0.2 rad. The reason is that a proportional controller is utilized for position control,and it has no integrator. The steady-state error of load variation is related to the magnitude of the load disturbances.With LADRC,the position drops to 199.9 rad,but the observed disturbance ^d(t)changes quickly,and the position is readjusted to the command 200 rad after 0.4 s. Because the structure of the controlled object is modified to a cascade integral form system by the disturbance observer,it is consistent with the theoretical analysis in Section 4.3. Therefore, LADRC has a better load torque disturbance rejection property than that of Baseline. Firstly, acceleration feed-forward with the tracking differentiator for a time-varying command is tested. Fig. 20 shows experimental results of different methods with a sinusoidal reference θref=5sin(6πt)[1-exp(-15 t3)] rad, and r=50 in the TD. In the tracking process, the maximum θerris 0.08 rad with acceleration feed-forward (Baseline), and it is smaller than 0.29 rad under Basic (without acceleration feed-forward). This is consistent with theoretical analysis and simulation results. Fig. 20 Experimental results of acceleration feed-forward verification with θref=5sin(6πt)[1-exp(-15 t3)] rad. Fig. 21 shows experimental results of parameter uncertainties with a sinusoidal reference θref=5sin(6πt)[1-exp(-15 t3)]rad. With matched parameters (see Fig. 21(a)), the two methods are close to each other, and the range of the observed disturbance is-326 to 323.In order to simulate the condition of a mismatched flux linkage, the flux linkage ^ψrin the DSP software is set to 2ψrninstead of modifying the permanent magnet of the PMSM. A better robustness is achieved under an unmatched inertia J and an unmatched flux linkage ψr. Fig. 21 Experimental results of θref=5sin(6πt)[1-exp(-15 t3)]rad with parameter uncertainties. Fig.22 Experimental results of low-speed tracking performance. Here, the differences between the simulation and experimental results are analyzed. In simulation, the quantization error caused by the Resolver-to-Digital Converter (RDC) is not taken into account when the rotor position is sampled,and the measured position θ and speed ωrhave higher resolutions. However, in experiments, the AD2S1200 is used to acquire the position θ, which is a 12 bit resolution RDC. A quantization error is introduced. Therefore, the waveforms of position and speed in the experiments are not as smooth as those in simulation. Meanwhile, there are more complex nonlinear dynamics in an actual motor system,but the PMSM model in simulation is an ideal mathematical model, so the observed disturbances of LADRC in experiments are slightly different from those in simulation, but the trend and magnitude of the observed disturbances in experiments and those in simulation are basically the same. Consistent with the simulation, a low-velocity trajectory is given as follows: θref=20sin(0.2πt) rad, and experimental results are shown in Fig. 22. Due to static friction, the speed is distorted at the zero crossing. The distortion rate of speed is higher with Baseline than that of LADRC.When the PMSM reverses, θerris 0.2 rad with Baseline, so even with low speed and unmodeled static friction disturbances, an excellent robustness performance is achieved with LADRC. This paper has proposed a high-dynamic servo system based on LADRC dedicated for EMA application in aircraft. The proposed LADRC-based double-loop method, which takes disturbances including nonlinearity or unmodeled uncertainty into account, guarantees an EMA system robustness under mechanical inertia and load torque variations. Acceleration feed-forward through a tracking differentiator improves the dynamic response to position instructions. The IAE of LADRC is more competitive than those of Basic and Baseline in simulation and experimental results. This has clearly demonstrated that the proposed control system can give a better transient performance in comparison with the Baseline controller in the case of mechanical parameter and load torque variations. Acknowledgements This work was supported by the Shaanxi Provincial Key R&D Program, China (No. 2017KW-ZD-05), the Natural Science Basic Research Plan in Shaanxi Province of China (No.2018JQ5187), and the Fundamental Research Funds for the Central Universities, China (Nos. 3102017JC06004,3102017OQD029).Meanwhile,the authors are grateful to editors and reviewers for their helpful comments.4.3. Composite control law based on LADRC





4.4. Gain frequency response analysis



4.5. Disturbance rejection



4.6. Discretization algorithm for digital implementation

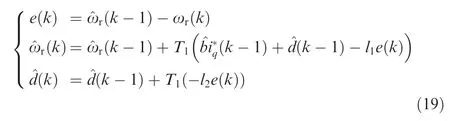


5. Simulation results

5.1. Set-point tracking and load disturbance suppression performance



5.2. Time-varying position tracking
5.3. Low-velocity friction torque rejection
6. Experimental results

6.1. Set-point tracking test




6.2. Time-varying tracking test


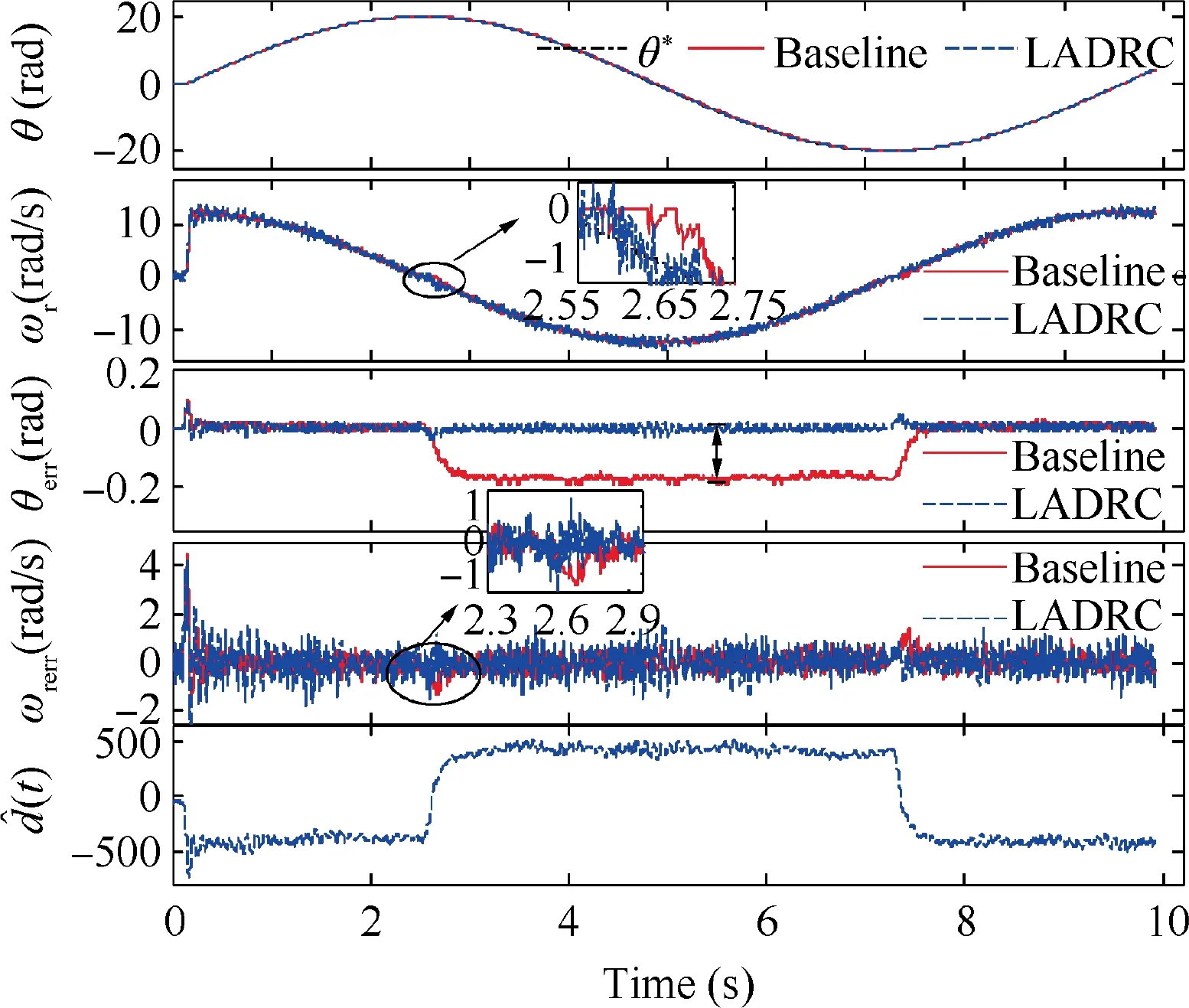
6.3. Low-velocity friction torque rejection test
7. Conclusions
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Heading control strategy assessment for coaxial compound helicopters
- An adaptive integration surface for predicting transonic rotor noise in hovering and forward flights
- An algorithm to separate wind tunnel background noise from turbulent boundary layer excitation
- Simulation of mass and heat transfer in liquid hydrogen tanks during pressurizing
- Leakage performance of floating ring seal in cold/hot state for aero-engine
- Six sigma robust design optimization for thermal protection system of hypersonic vehicles based on successive response surface method
