An adaptive integration surface for predicting transonic rotor noise in hovering and forward flights

Siyu CHEN, Qijun ZHAO, Yiyang MA

National Key Laboratory of Rotorcraft Aeromechanics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS FW-H_pds equations;Integration surface;Navier-Stokes equations;Rotor;Transonic rotor noise

Abstract In this paper,a new permeable adaptive integration surface is developed in order to evaluate transonic rotor noise in accordance with FW-H_pds equations (Ffowcs Williams-Hawkings equations with penetrable data surface). Firstly, a nonlinear near-field solution is computed on the basis of Navier-Stokes equations, which is developed on moving-embedded grid methodology.The solution calculated through the present CFD method is used as the input for acoustic calculations by FW-H_pds equations. Then, two criteria for constructing integration surfaces are established based on the analysis of the quadrupole source strength and the nonlinear characteristic.A new surface is determined adaptively by the pressure gradient or density in a given flowfield,eschewing the uncertainties associated with determining cylinder-shaped integration surfaces. For varying hover cases,transonic noises are simulated with new integration surfaces for a UH-1 model rotor. Furthermore, numerical results of the new integration surface derived from the density perturbation value conform better to experimental data than results derived from the pressure gradient.Finally, the integration surface given by ∇ρ｜ ｜being 0.1, which is an applicable criterion obtained from hover cases,is used to predict transonic rotor noise in forward flight.The computational accuracy of the new integration surface method has been validated in predicting transonic rotor noise of an AH-1 model rotor at different advance ratios.

1. Introduction

Modern helicopter designs have an unprecedentedly urgent requirement for both high aerodynamic performance and low noise radiation.1Accurate evaluations of rotor noise are the prerequisites for the design of an advanced rotor with low noise.

In recent years, great progress has been made in the study of rotor noise. Several integral methods for predicting rotor noise are available these days, including the classical Ffowcs Williams-Hawkings (FW-H) equations,2the Kirchhoff approach,3and the FW-H_pds equations (Ffowcs Williams-Hawkings equations with penetrable data surface).4All the three aforementioned integral methods rely on a Computational Fluid Dynamic (CFD) solution as input to predict acoustic near and far fields.

The Lighthill acoustic analogy, as expressed by the FW-H equations,has been utilized for nearly half of a century.While the FW-H equations outweigh other frequently-used methods in predicting subsonic noise, unfortunately, when it comes to the prediction of HSI noise in transonic flow,the FW-H equations can provide evaluations of little,if not none,significance.Such an absence of applicable predictions could be explained by the fact that nonlinear volume quadrupole terms are neglected, and the FW-H method is regarded as a linear approach.5The Kirchhoff method has been used in the prediction of transonic rotor noise, in which surface source terms alone are sufficient to produce reliable predictions. However,the Kirchhoff surface, which is required to be located within the linear flow region,turns out to be an obstacle to furthering its utilization, for the linear region is difficult to demarcate.6Theoretically, while the Kirchhoff surface should be far enough from the rotor to guarantee its location being within the linear region, the accuracy of CFD solutions is vitiated as the distance between the rotor and the Kirchhoff surface increases. Moreover, the relationship between Kirchhoff source terms and thickness, loading, nonlinear effects, or indeed any physical mechanism,inevitably eludes observation.The FW-H_pds equations, which are derived from the FW-H equations with a permeable surface,have been steadily gaining ascendancy over the other two methods. Such a prevalence is due to the facts that the integration surface can extend beyond the linear region,and the nonlinearities in the inner FW-H_pds surface can be taken into account.7Therefore, the FW-H_pds method appears to be a better choice when evaluating transonic rotor noise.On the basis of the FW-H_pds method,previous studies have achieved further progresses in both theoretical analysis and practical application.Han et al.8compared different aeroacoustic methods of predicting rotor noise in hover and forward flights. For different choices of rotating the integration surface,it has already been shown that the FWH_pds method is more reliable than the Kirchhoff method.Ianniello9paid attention to the singular behavior of the FWH equation at supersonic speeds, and coupled the advantages of the FW-H_pds equation to an emission surface integration scheme. Song et al.10applied the CFD/FW-H_pds method to the aerodynamic/acoustic optimization of the rotor blade tip.Huang et al.11developed a time-domain analytic formulation,which is a new solution of the convective FW-H equation, to predict the radiated noise from supersonically-rotating sources in a subsonic moving medium. Recently, High-Speed Impulsive (HSI) noise radiated from rotors with high tip speed has been predicted by a frequency domain solution12of the permeable FW-H_pds equation.

Although great progresses have been made in the development of the FW-H_pds method, a disadvantage of such a method cannot be ignored.Theoretically,once the main quadrupole sources are included in the surface,the placement of the integration surface for the FW-H_pds method is a matter of convenience. However, CFD solutions tend to become more inaccurate as the integration surface is placed further away from the body.13Thus, the location of the FW-H_pds surface is usually a result of the reconciliation of conflicting factors.A small cylinder surface cannot take all the nonlinearities into account, while a cylinder surface that is big enough may give rise to other problems, such as the inaccuracy of input data in the far field or the singularity appeared in equations. In short, the results of the FW-H_pds method are very susceptible to the location of the integration surface.

In order to avoid the aforementioned uncertainties, this paper presents two criteria for determining the integration surface to obtain a stable and accurate acoustic solution.The criteria, which are related to density perturbation and pressure gradient respectively, are established based on an analysis of the quadrupole sources strength and the nonlinear characteristic. Furthermore, the two criteria for constructing integration surfaces are attempted and compared by hover cases of a UH-1 model rotor.Combining calculation results and theoretical analysis, a certain criterion is obtained, and the efficiency and reliability of this criterion can be proven by hover cases.Finally,this certain criterion is adopted in predicting transonic rotor noise of an AH-1 model rotor at different advance ratios in forward flight.Numerical results show that the new integration surface derived from density perturbation conforms better to experimental data than previous results obtained by traditional integration surfaces. It means that in comparison with a cylinder-shaped integration surface, an adaptive integration surface can reach a higher accuracy in the prediction of HSI noise in both hovering and forward flights.

2. Aerodynamic method

The CFD/FW-H_pds method has been put into use in the prediction of transonic rotor noise.14The unsteady flowfield of a rotor can be obtained by solving three-dimensional RANS equations with the Spalart-Allmaras turbulence model based on an embedded grid system. Therefore, in the near field, a pressure signal can be directly extracted from the Navier-Stokes solution. On the other hand, the sound propagation to the far field can be calculated with the FW-H_pds method,which uses a rotating integration surface to eschew interpolation errors.

2.1. Moving-embedded grid method

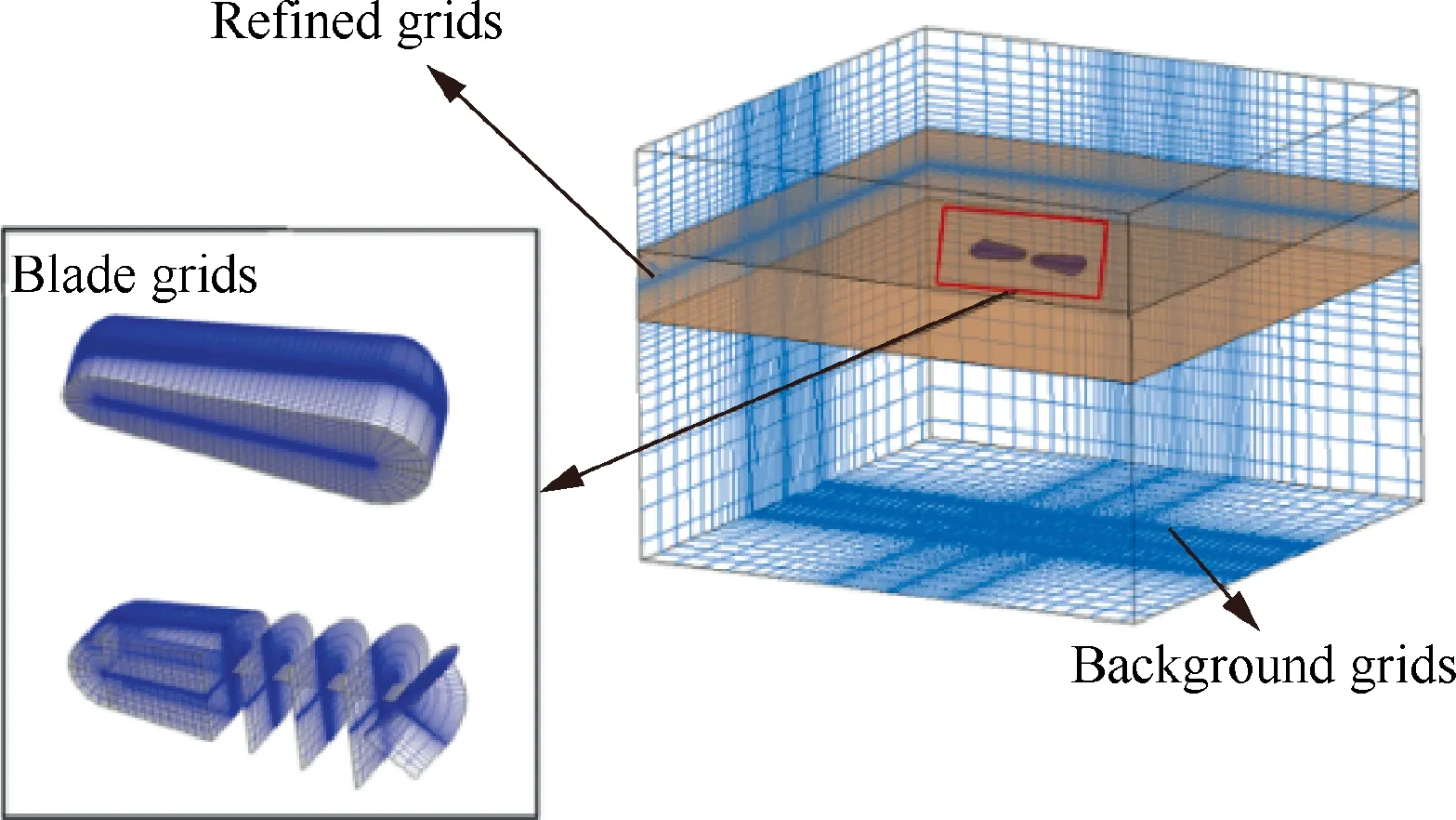
Fig. 1 Sketch of an embedded grid system.

Fig. 1 shows a moving-embedded grid system, which is composed of body-fitted grids around the blade and Cartesian rectangular background grids. The C-O-type blade grids are established by using an optimum geometry algorithm to interpolate and rotate airfoil grids which are generated by solving Poisson equations. The blade grids include 122 points in the spanwise direction, 100 points in the normal direction, and 207 points in the chordwise direction. The background grids have 180×150×120 points. To keep a balance between the grid size and the calculation accuracy,an adaptive grid method is introduced.15Since some variables in the governing equations vary rapidly in the blade tip region, grids in this region are refined adaptively. To build a relationship between the blade grids and the background grids, the inverse map and Pseudo-Searching Scheme of Donor Elements (PSSDE) methods are used.16The rigid blade rotating and pitching motion and the viscous effects could be taken into consideration by solving Navier-Stokes equations over the moving-embedded grids.

Fig.2 Comparisons of aerodynamic characteristics of Helishape 7A rotor between numerical results and experimental data.

Fig. 3 Pressure coefficient Cp distributions on blade surface at Matip =0.610 for two radial sections.

2.2. CFD method

The flowfields of a rotor in both hovering and forward flights are calculated by solving three-dimensional RANS equations based on an embedded grid system. Navier-Stokes equations are formulated in a rotation coordinate system, and could be written in finite-volume forms as where W denotes the conservative variable, and Fcand Fvdenote convective and viscous fluxes, respectively.

Third-order monotone upwind interpolation (MUSCL scheme) is used to obtain a more accurate interpolation.Besides, Roe's approximate Riemann solver is employed to reduce computational costs in the exact solution of the Riemann problem. The flux-difference splitting schemes evaluate the convective fluxes at a face of the control volume from the left and right states by solving the Riemann problem.

The implicit LU-SGS method is used in the sub-iteration step in order to improve the computational efficiency.17The k-ω-SST turbulence model is used to calculate the turbulence viscosity.

Fig. 4 Pressure coefficient Cp distributions on blade surface at Matip =0.877 for two radial sections.

Fig. 5 Pressure coefficient Cp distributions on blade surface at Matip =0.644 for various radial sections.

2.3. CFD case

A four-bladed Helishape 7A model rotor and a two-bladed Caradonna-and-Tung (C-T) model rotor have been used as validation test cases for evaluating the accuracy of the CFD method in hover. In addition, an AH-1 model rotor is used as a forward validation test case.Comparisons between calculated results and experimental data are made in this section.

The Helishape 7A rotor blades have a chord length of 140 mm, a linear aerodynamic twist of -3.95 (°)/m, a square tip, and a rectangular planform.18The rotor diameter is 4.2 m. The test conditions used for the computations included in the present paper are given by Matip=0.662 and θ0.7=7.5°.Fig.2 shows comparisons of aerodynamic characteristics of the Helishape 7A rotor between numerical results and experimental data. FM denotes the hover efficiency, and CTdenotes the thrust coefficient.

The C-T rotor employs two cantilever-mounted, manually adjustable blades, which are untwisted and untapered, with NACA0012 airfoil sections.19The rotor radius is 1.143 m,and the chord length is 0.191 m; thus, the rotor blade aspect ratio is 6. Two cases for the C-T rotor are considered:Matip=0.610 and Matip=0.877. In Figs. 3 and 4, the calculated chordwise surface pressure distributions of the C-T model rotor for two radial sections (r/R=0.5 and r/R=0.96) are compared with the experimental data,respectively.20

Fig.6 Locations of integration surfaces with respect to the rotor blade.

The AH-1 rotor has a scale of 1/7,two rectangular linearly twisted blades with an aspect ratio of 9.22 and slightly modified NACA0012 profiles. The rotor radius is 0.958 m with a chord of 0.1039 m.Further details are given in Ref.21.The following case for this rotor is considered: μ=0.164 and Matip=0.644.Fig.5 compares the calculated chordwise surface pressure distributions for the AH-1 model rotor with the experimental data for two radial sections(r/R=0.6 and r/R=0.91)22,where ψ is the azimuth angle. From Figs. 2-5, we can find that the predictions are in excellent agreements with the experimental data in both hovering and forward flights,which provide a solid basis for predicting rotor noise.

Fig.7 Predicted sound pressures using FW-H_pds equations with varying integration surface locations:predictions are for an in-plane observer located 3.09R from the rotor hub in hover.

3. Acoustic method

The FW-H method is efficient when applied to low-speed predictions.23However, because of the omission of nonlinear effects in the near field of the rotor, HSI noise predictions are not possible.The Kirchhoff method can be used for predictions of transonic rotor noise, but it is hyper-sensitive to the choice of integration surface.24The Kirchhoff surface has to be chosen in the linear flow region. The location of the linear region,however,is not well delimited.Thus,the Kirchhoff surface has to be located at a distance long enough away from the rotor to make sure that the propagation can be governed by the linear wave equation outside the surface itself, but CFD solutions could hardly reach the desired computation accuracy in the far field.The FW-H_pds method is more robust,and the integration surface could be placed anywhere in the flowfield,provided that the key quadrupole source is included. The FW-H_pds method,on the other hand,is an accurate and efficient implement to predict transonic rotor noise. Therefore,the FW-H_pds method can be further exploited for the following research.

3.1. FW-H_pds method

The FW-H_pds equations can be transformed into an integral representation of the solution which is known as the permeable surface form of Farassat's Formulation 1A.25

where

Fig. 8 Contours of the UH-1 model rotor at a cross section of 0.9R.

When the selected integration surface contains the nonlinear flow, p′T, p′Land p′Qwill lose physical meaning and have only mathematical significance. The contribution of quadrupole noise caused by the non-linear flow will be reflected from the first two terms,p′Qwill be approximately zero,and the sum of the first two terms will be the total rotor noise. dS denotes element of the integration surface area.

where ρ is density of fluid,uiis components of local fluid velocity,un=ui^ni,and vnis local normal velocity of source surface.Pijis compressive stress tensor. Ma is the surface Mach number,and r is the distance between the observer and the source.c0is the speed of sound in the undisturbed medium. The subscript ‘‘ret” means the quantity evaluated at retarded time.f=0 means the function that describes the integration surface.The dots on ˙Lr, ˙Un,and ˙Mardenote the rate of variation with respect to source time. LMa=LiMai, and a subscript r or n indicates a dot product of the vector with the unit vector in the radiation direction^r or the unit vector in the surface normal direction ^n, respectively.

The pressure data extracted from the Navier-Stokes solution can be used as the FW-H_pds surface data without interpolation.The nonlinearities in the inner part of the FW-H_pds surface can be taken into account. The choice of the FWH_pds surface location is, therefore, connected with the range of the nonlinear effects.Another factor in determining the surface location is the accuracy of the input data obtained from the Navier-Stokes equations.

Fig. 9 Adaptive integration surfaces given by different contour lines.

3.2. Cylinder shape integration surface

Two types of integration surfaces have been used in the implementation of the FW-H_pds integral for helicopter rotor noise prediction. Their difference lies in whether or not the surface rotates with the helicopter blades. It has been confirmed that these two integration surfaces yield similar results.

The purpose of this paper is to explore the effect of different integration surfaces on the accuracy of noise calculation. In order to avoid introducing additional uncertainties in the interpolation of nonrotating integration surfaces, a rotating integration surface surrounding the entire rotor is applied in this paper. With this rotating surface, interpolation errors can be avoided, and the key quadrupole sources in the near field of the rotor can be included.

Several surface locations, which correspond to grid lines,are evaluated in this work.Fig.6 shows four different rotating integration surface locations that range from 0.25 to 1.2 airfoil chord lengths off the blade surface.

The acoustic pressure predictions of the UH-1 model rotor for each of these surface locations are shown in Fig. 7. robsis the distance from the observation point to the center of the rotor. The FW-H_pds solution varies in relation to the location of the integration surface.Comparisons of sound pressure time histories with experimental data show the same trend as observed.However,the negative peak value of sound pressure is progressively underestimated as the integration surface approaches the blade surface, for some non-linear terms are neglected. Brentner came to similar conclusions in Refs.4,8.However, if the integration surface is too far from the blade,problems such as inaccuracy of input data in the far field and possible singularity may arise. The singularity is due to Mar=1, when a rotating grid extends far from the blade tip. There is a Doppler singularity ｜1 -Mar｜in the denominator of the integrand. Therefore, the outer radial boundary of the integration surface should not be too far from the blade in order to keep the integration surface from moving supersonically for high-speed transonic rotors. Consequently, more attention should be paid to the determination of the FW-H_pds integration surface, for the results obtained are subject to manual modifications.

3.3. Permeable adaptive integration surface

The previous section has proven the conclusion that the FWH_pds solution varies in relation to the location of the integration surface. However, the location of the FW-H_pds surface is uncertain, which is determined artificially. As a result, the sound pressure calculated with the surface being set manually is also influenced by artificial factors.

To avoid the aforementioned uncertainties, a new method to construct permeable adaptive integration surfaces is developed,in which the shape and location of an integration surface are thoroughly determined by the flowfield itself rather than being set manually. The integration surface could be determined in accordance to the following principles.

(1) The integration surface should include the nonlinear area near the blade where main quadrupole sources are located as much as possible,so as to acquire the total noise including the non-linear contribution.

(2) The integration surface should be as close as possible to the blade to obtain more accurate information of the flowfield, so as to improve the accuracy of noise evaluation.

Following the above principles, the criterion for determining the integration surface should be established on the analysis of the strength of the quadrupole source,because,if we use a surface that encloses the blade and the volume of intense quadrupoles, then we can accurately calculate the acoustic pressure, on the assumption that the weak quadrupoles excluded from the surface could be neglected.

In order to understand the strength of quadrupole sources,we can start with Lighthill's equation26as follows:

Fig. 10 Predicted sound pressures with varying integration surfaces given by different contours (robs/R=3.09).

Fig. 11 Comparison of predicted sound pressure time histories using permeable adaptive integration surfaces given by the contours of∇p｜ ｜=0.8 and Δρ｜ ｜=0.1 with experimental data.

If any solid boundaries which may be present do not influence the sound field to any appreciable extent, the solution to Lighthill's equation is

where

In order to transform this result into a more suitable form,it is convenient to introduce the differential operator δ/δyi,which denotes partial differentiation with respect to yi, with both t and R held fixed, to obtain

Now suppose that the operator ∂/∂yidenotes partial differentiation with respect to yiwith x and t held fixed.Then,since∂/∂xidenotes partial differentiation with respect to xiwith y and t held fixed,the chain rule for partial differentiation shows that

Hence, for any function F(y，R，t),

Using this result in Eq. (8) yields

The notation [Tij] is used to denote Tij(y，t-R/c0). Notice that each of the first three integrands is the divergence of a vector, while the divergence theorem shows that

where SRdenotes a sphere of radius R,and A denotes any vector for which the integrals exist.Hence,upon assuming that Tijis smooth,we can conclude that the first three integrals vanish.As a consequence,

where

Additionally, Eq. (13) becomes

Replace RiRj/R3with xixj/x3to obtain

Eq. (17) has been cast into a form which correctly displays the true quadrupole structure of the sound sources. We can conclude that the size of the fluctuating density ｜ρ -ρ0｜is closely related to the strength of the quadrupole source. The region where an intense quadrupole source is located has a greatly-fluctuating density. Thus, the locations of intense quadrupole sources could be more accurately explored using the size of the fluctuating density ｜ρ -ρ0｜.

We define density perturbation ｜Δ ρ｜= ｜ρ -ρ0｜/ρ0to denote the rate of change of the local density relative to the steady background flow density. Considering the relationship between the fluctuating density and the strength of a quadrupole source, we suppose that the integration surface may be determined by Δρ｜ ｜. In addition, the nonlinear region has displayed intense variations of flow field information:the pressure varies rapidly in the nonlinear region, especially in the area near the shock wave.Therefore,the magnitude of the pressure gradient ∇p｜ ｜may also be used as a criterion to determine the integration surface. The aforementioned two criteria for constructing integration surfaces are attempted and compared by hover cases of the UH-1 model rotor.

Fig.8(a)and(b)give the pressure gradient contour and the density distribution of the UH-1 model rotor at a cross section of 0.9R with a hover blade-tip Mach number of 0.88,respectively.

Fig.12 Comparison of predicted peak values of sound pressures using permeable adaptive integration surfaces given by the contours of ∇p｜ ｜=0.8 and Δρ｜ ｜=0.1 with experimental data.

Fig. 13 Density contour of the AH-1 model rotor.

Fig. 14 Adaptive integration surfaces at various azimuthal angles given by the contour of Δρ｜ ｜=0.1.

As illustrated in Fig. 8, when the contour line of ∇p｜ ｜or Δρ｜ ｜being a certain value,the integration surface is determined with the presupposition that the area within the contour line is nonlinear,and the grids adjacent to the contour line are taken as the integration surface.For contour lines with different ∇p｜ ｜or Δρ｜ ｜values, the integration surfaces are similar in shape while differ slightly in size.Fig.9(a),(b),(c),and(d)show four integration surfaces given by the contour lines of ∇p｜ ｜being 0.6, 1.0 and Δρ｜ ｜being 0.05, 0.15, respectively.

To find out whether or not determining the nonlinear area by the pressure gradient is more reasonable than by the density disturbance, the sound pressures of the UH-1 model rotor are simulated, at a hover tip Mach number of 0.88, with integration surfaces given by ∇ρ｜ ｜being 0.6, 0.7, 0.8, and 1.0 respectively. The integration surfaces given by Δρ｜ ｜being 0.05, 0.10,0.15,and 0.20 are also simulated in the same condition.Fig.10(a) and (b) show the predicted sound pressure time histories with different integration surfaces in comparison to experimental data.The sound pressure time histories show the same trend, and the waveforms with ∇p｜ ｜being 0.8 and Δρ｜ ｜being 0.1 conform to the experimental data very well. When ∇p｜ ｜is 1.0 or ｜Δ ρ｜is 0.05, the negative peak value is obviously underestimated, for some nonlinear terms are neglected.

The contour of ∇p｜ ｜being 0.8 and the contour of Δρ｜ ｜being 0.1 are chosen to determine the adaptive integration surface.Fig. 11 compares the predicted sound pressure time histories using these two adaptive integration surfaces respectively with the experimental data at different tip Mach numbers and observer locations.

The differences of positive and negative peak values are shown in Fig. 12. It can be observed that the predicted results with the integration surfaces derived from the contour of Δρ｜ ｜being 0.1 conform better to the experimental data in capturing the peak values of the sound pressure.

In the above calculations, the transonic rotor noises of the UH-1 model rotor at various tip Mach numbers and observer locations in hover are simulated, with integration surfaces given by different contours of ∇p｜ ｜and Δρ｜ ｜respectively. The calculated results demonstrate that the time histories show the same trend, but the waveform with the contour of Δρ｜ ｜being 0.1 conforms to the experimental data better. Given the relationship between the strength of a quadrupole source and the fluctuating density, the region where an intense quadrupole source is located has a greatly-fluctuating density. We can suppose that Δρ｜ ｜≥0.1 could be regarded as a symbol of the region where intense quadrupole sources are located. Therefore, the contour of Δρ｜ ｜ being 0.1 is an adaptive criterion for predictions of transonic rotor noise in hover. Therefore, this criterion is chosen for determining the control surface to predict the transonic rotor noise of the AH-1 model rotor in forward flight.

Fig. 13 gives the density distribution of the AH-1 model rotor at a cross section of 0.9R with an advance ratio of 0.345 at an azimuthal angle ψ of 300°. As illustrated in Fig. 13, when the contour line of ｜Δ ρ｜being a certain value,the integration surface is determined with the presupposition that the area within the contour line is nonlinear, and the grids adjacent to the contour line are taken as the control surface.

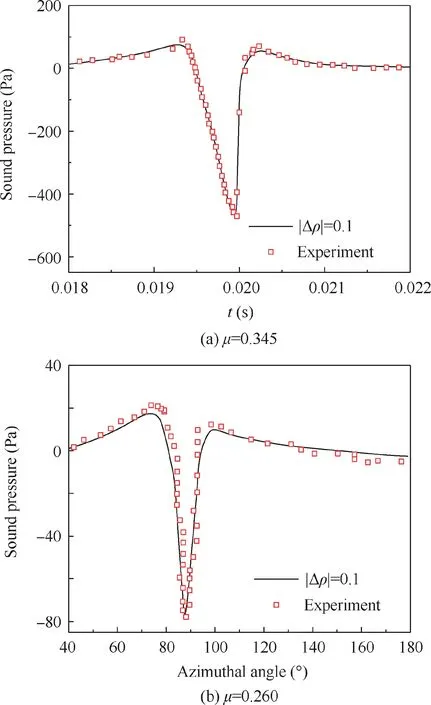
Fig. 15 Comparison of predicted noise time histories using permeable adaptive integration surfaces given by the contours of Δρ｜ ｜=0.1 with experimental data.

For contour lines with different values,integration surfaces are similar in shape while differ slightly in size. Fig. 14 shows integration surfaces of the AH-1 model rotor (μ=0.345) at various azimuthal angles given by the density contour line of Δρ｜ ｜being 0.1.

It can be seen from the given adaptive integration surfaces schematic diagrams that, when the blade is located between azimuthal angles of 60° and 120°, the integral range is relatively large. On the contrary, when the blade is located between azimuthal angles of 240° and 300°, the integral range is relatively small. The integral range is the largest when the blade is at an azimuthal angle of 90°. This is because that,when the helicopter is flying at a medium speed, owing to the larger tip Mach numbers in the advancing side,the nonlinear effects are more serious. The range of integration surface should be big enough to include the strong quadrupole as much as possible. In order to calculate more conveniently,the integration surface of 90° is taken as the control surface for noise calculation.

Fig. 15 compares the predicted noise time histories using adaptive integration surfaces with the experimental data at different advance ratios and observer locations. It can be observed that the predicted results with the integration surfaces given by the contour of Δρ｜ ｜being 0.1 conform to the experimental data very well.

4. Conclusions

To evaluate transonic rotor noise, a novel permeable adaptive integration surface method is introduced on the basis of the FW-H_pds method. The nonlinear near-flowfield solution is efficaciously calculated by an N-S solver,and subsequently utilized as the input data for acoustic calculations by FW-H_pds equations. An adaptive integration surface, determined by pressure gradient or density perturbation, is developed for the prediction of transonic rotor noise at different tip Mach numbers and observer locations. Some conclusions are obtained as follows.

(1) The FW-H_pds method appears to be a better choice in evaluating transonic rotor noise.However,the results of the FW-H_pds method show a certain sensitivity to control surface locations. If the location of the FW-H_pds surface is set manually,as a result,the calculation accuracy is also influenced by artificial factors.

(2) A novel permeable adaptive integration surface method is introduced,in which the shape and location of an integration surface are thoroughly determined by the flowfield itself rather than being set manually. Compared with the traditional cylinder-shaped integration surface,this novel adaptive integration surface, whether it is determined by pressure gradient or density, can remove artificial factors and obtain a stable acoustic solution.

(3) The strength of a quadrupole source is closely related to the size of the fluctuating density. The region where an intense quadrupole source is located has a greatlyfluctuating density.It is concluded from calculation that｜Δ ρ｜≥0.1 can be regarded as a reliable signpost of the region where intense quadrupole sources are located.Moreover, acoustic results obtained from the adaptive integration surface with ｜Δ ρ｜=0.1 have demonstrated greater accuracy compared with previous results with traditional integration surfaces. This method of constructing adaptive integration surfaces for noise evaluation by FW-H_pds equations is effective and reliable in both hover and forward flights.

Acknowledgements

This research has benefited greatly from the supports of the National Natural Science Foundation of China (Nos.11272150 and 11572156), and the Scientific Research Innovation Program of Jiangsu Province of China (No.KYLX15_0250).