An active damping vibration control system for wind tunnel models

Wei LIU, Mengde ZHOU, Zhengqun WEN, Zhung YAO, Yu LIU,Shihong WANG, Xiochun CUI, Xio LI, Bing LIANG, Zhenyun JIA

a Key Laboratory for Precision and Non-traditional Machining Technology of the Ministry of Education, Dalian University of Technology, Dalian 116024, China

b AVIC Aerodynamics Research Institute, Shenyang 110034, China

KEYWORDS Accelerometer;Active damping;Sting vibration;Transonic wind tunnel;Vibration active control

Abstract In wind tunnels, long cantilever sting support systems with low structural damping encounter flow separation and turbulence during wind tunnel tests, which results in destructive low-frequency and big-amplitude resonance, leading to data quality degradation and test envelope limitation. To ensure planed test envelope and obtain high-quality data, an active damping vibration control system independent of balance signal based on stackable piezoelectric actuators and velocity feedback using accelerometer,is proposed to improve the support stability and wind tunnel testing safety in transonic wind tunnel.Meanwhile,a design of powerful sting-root embedded active damping device is given and an active vibration control method is presented based on the mechanism analysis of aircraft model vibration. Furthermore, a self-adaptive fuzzy Proportion Differentiation (PD) control model is proposed to realize control parameters adjustment automatically for various testing conditions. Besides,verification tests are performed in laboratory and a continuous transonic wind tunnel. Experimental results indicate that the aircraft model does not vibrate obviously from -4° to 11° at Ma=0.6, the number of useable angle-of-attack has increased by 7° at Ma=0.6 and 5° at Ma=0.7 respectively, satisfying the requirements of practical wind tunnel tests.

1. Introduction

In many performance tests performed in wind tunnel, to reduce the aerodynamic interference of sting support system on test section flow around aircraft model, the length of the cantilever sting, particularly in transonic tunnels, usually varies from about 3 to 5 times the length of the aircraft model.1With the increasing of sting length, the structural damping of cantilever sting is lower. As aircraft model sweeps to big angle-of-attack and flow separation appears over the wings,in addition to any excitation of flow turbulence or support system shake,2the long cantilever sting support systems modes couple with the wideband excitations1-3and vibrate undesirably. It is a kind of low-frequency and big-amplitude vibration at the first resonant frequency3mainly in pitch plane3,4that results in wind tunnel balance working disorder or overloads and poor data quality.Consequently,the undesirable vibration will cause aircraft model-balance-sting systems to fatigue destruction,and the test safety will suffer the serious threat if the test is not stopped immediately.5,6Moreover, many performance tests of wind tunnel model are severely affected, and the planned test envelopes are constrained to be reduced.1,2Therefore,it is important to develop a vibration control method and system to counteract vibration within desirable range.

Vibration control has attracted more attentions from many researchers. Based on the vibration control mechanism, the vibration control methods of the long cantilever sting support systems can be divided into two categories: Passive Vibration Control (PVC) and Active Vibration Control (AVC). In the PVC methods,first proposed by Igoe and Capone,the passive devices with simple structures were installed inside the aircraft model without power input to attenuate the support system vibration.7However, only limited success was achieved due to low response, while it is desired that the vibration control system has rapid response speed, good real-time performance and high efficiency. With the advent of piezoelectric materials,8-10AVC methods were promptly applied to the long cantilever sting support systems.1

Hefer first conducted experimental investigations in European Transonic Wind tunnel (ETW) using a simple spring/-mass system excited by piezoelectric elements.2,11-13An active interface,named Anti Vibration System(AVS),is developed to counteract aircraft model vibration, with the help of the integrated piezoelectric elements controlled by a digital control system using the balance signals. Due to its structural limitation, AVS system was less effective for strong vibrations in pith plane.2,14To overcome the limitations, another system(AVS II)located downstream in the sting was developed,mentioned by Schimanski and Quest,15but no details have been reported. To further research, Balakrishna et al. developed a damper similar to AVS in ViGYAN's low speed wind tunnel,and a series of experimental wind tunnel evaluation were conducted.1,16,17Then, the vibration control technology was applied to Pathfinder-1 model and Crew Launch Vehicle(CLV)model and Common Research Model(CRM)in succession at the NASA Langley Research Center National Transonic Facility (NTF) and Ames Research Center 11×11 Foot Transonic Wind Tunnel, and the pitch polar sweep data showed reduced vibration and some improved angle-of-attack testing range. Still, the feedback and control of the damper depended on balance signals and test measurement system in wind tunnel similarly.Additionally,the damper design aspects of the CRM model were detailed from a sting damping energy view point.17However, the vibration of long cantilever sting support systems is a dynamic problem and the AVC method strengthens the characteristics of the long cantilever sting support systems, it is difficult to evaluate the characteristic improvement of system itself from energy view point. Besides,Chen et al.presented an active vibration control system based on self-developed electromagnetic actuator and accelerometer,the electromagnetic actuator was installed inside large-scale aircraft model.18-20However, the large size of the electromagnetic actuator limits its applications. Shen et al. developed an active damper based on piezoelectric stack actuators using balance signal as feedback by Proportion Integration Differentiation (PID) and Back Propagation Neural Network (BPNN)controllers in a low speed wind tunnel.21,22Then validation of active sting damper was conducted in a transonic wind tunnel,90%energy elimination of sting mode frequency has been attained and the operational range of angle-of-attack was expanded by 1.5°.22The research mainly concentrates on the control strategies by employing balance signal feedback.

Many scholars have investigated innovations in active damper devices and methods for the long cantilever sting support systems in wind tunnel. However, in terms of the existing system, the feedback signals and control of the damper still depends on balance signal in wind tunnel,the operational range of angle-of-attack is still not ideal and the control method cannot satisfy various testing conditions. In fact, the balance signals come from dynamic strain gauge balance. However, the dynamic strain gauge balance has a low dynamic response and a poor dynamic stability due to its low damping and natural frequency. Thus, it is difficult to timely obtain accurate vibration data from poor balance signals,especially under violent vibration.Moreover,the existing system is not usable in the wind tunnel tests without balance.Then,in this paper,an active damping vibration control system independent of balance signal, based on stackable piezoelectric actuators and aircraft model velocity feedback using accelerometer, is proposed to counteract the main vibration in pith plane to ensure the planed test envelope.Meanwhile,a self-adaptive fuzzy Proportion Differentiation(PD)control method is proposed to automatically adjust the parameters for various testing conditions.

The remainder of this paper is organized as follows. Section 2 introduces the active damping vibration control system employing stackable piezoelectric actuators and aircraft model velocity feedback using accelerometer.Section 3 introduces the principle of the active vibration control method,and the active vibration control system is modeled and analyzed from a viewpoint of dynamics.In Section 4,a self-adaptive fuzzy PD control method is proposed to realize parameters adjustment automatically for various testing conditions. Section 5 experiments are conducted to verify the performance of the active vibration control system as well as the stability both in laboratory and a continuous transonic wind tunnel. Finally, some conclusions are given in Section 6.

2. Active damping vibration control system

In this paper,an active damping vibration control system independent of the test measurement system in wind tunnel, with employing stackable piezoelectric actuators and aircraft model velocity feedback,is proposed for the long cantilever sting support systems to strengthen the resistance to vibration in pith plane. To provide a high resistance, a powerful sting-root embedded active damping device is designed,where four piezoelectric actuators embedded inside the root of the sting were employed to output dynamic force and displacement based on the velocity feedback from the mass center of aircraft model. Moreover, an accelerometer is used to obtained velocity indirectly.

2.1. Outline of the vibration control system

As shown in Fig. 1, the active damping vibration control system based on velocity feedback is an electro-mechanization system consists of an accelerometer, a real-time controller,two amplifiers, a principal computer and a sting with stingroot embedded active damping device. The accelerometer is set on the mass center of aircraft model in pith plane and the velocity of a real vibrating aircraft model can be obtained by integrating the acceleration signal. It can satisfy various testing conditions comparing to balance signal. The real-time controller is used as control decision system to receive velocity feedback and control the sting-root embedded active damping device through the two amplifiers to resist stochastic dynamic load in real time. Moreover, the real-time controller, the amplifiers and the principal computer are placed outside wind tunnel and the principal computer is used for algorithm development and real-time monitoring.

2.2. Design of sting-root embedded active damping device

The active damping device is the driving device of the active vibration control system that it has significant influence on the active vibration control effects. Then, design requirements of the active damping device are listed as follows: (A) the device cannot affect the sting aerodynamic configuration within laminar flow section to ensure test section flow around aircraft model; (B) the actuators must be installed in a limited sting structure,because of the narrow space inside the test section; (C) the power of actuators should be the largest possible powerful to resist unknown stochastic dynamic load changing with aircraft model,angle-of-attack and airflow speed;(D)The installation of actuators should ensure the reliable output of control force. According to those requirements, a sting-root embedded active damping device is designed in the root of sting outside the laminar flow section. With this mechanism,we select the stackable piezoelectric actuators which can output a force at kN level with a displacement at micron order under electrode voltage. In order to satisfy power requirements, four stackable piezoelectric actuators are incorporated into two groups. Mounting grooves for the stackable piezoelectric actuators are designed and the stackable piezoelectric actuators are embedded into the root of the sting directly.To further ensure the reliable output of control force and reduce the additional vibration, a pre-tightening mechanism is designed to embed in the mounting groove, with this mechanism, equivalent forces on stackable piezoelectric actuators can be applied by the torque wrench. The concrete structure of the active damping device is shown in Fig. 2.

The integration design of the sting-root embedded active damping device and sting realizes the well structural coupling between stackable piezoelectric actuators and sting. The output force of active damping device can be described as

where Kpieis the load rigidity coefficient, u(t) is the system input voltage and npieis the number of stackable piezoelectric actuators.

Fig. 1 Schematic diagram of active damping vibration control system.

Fig. 2 Assembly drawing of sting-root embedded active damping device.

3. Analysis of the active vibration control system

3.1. Principle of the active vibration control method

An active damping vibration control method based on piezoelectric actuator and velocity feedback for the long cantilever sting support system is presented in this paper.It is a vibration control method according to the loop control theory.

As shown in Fig. 3, M(t) is the dynamic bending moment,σ(t) and ε(t) represent the dynamic stress and dynamic strain,respectively. d is the distance from the neutral layer, f(t) and ΔL(t) respectively represent the output force and elongation of the stackable piezoelectric actuator. y, y0and y(t) are the displacement, static displacement and dynamic displacement,and Kvis the feedback coefficient. When the flow separation appears over the wings at a big angle-of-attack, the airflow around wings will change from laminar layer to turbulent layer through a narrow transition area, resulting in two types of forces. Namely, the static lift force perpendicular to airflow field direction and the wideband stochastic dynamic force excitated by the airflow turbulence. Then, the force vector acting on the aircraft model can be expressed as1

where CLpDS is the static lift force and CLrepresents lift coefficient changing over angle-of-attack, pDis the flight dynamic pressure, S is the wing area. p(t)S represented by Fexc(t) is the stochastic dynamic force excitated by airflow turbulence with multi-frequency components and p(t) represents the turbulence pressure.

Some frequencies of stochastic dynamic force Fexc(t) are closed to the resonant frequencies, which results in the coupling between multiple dynamic forces and modes of the long cantilever sting support system, as well as the low-frequency and big-amplitude vibration in the pitch plane.1-3Figs. 4 and 5 show pitch plane vibrations of a civil aircraft model at Ma=0.6 and Ma=0.7, respectively. As shown in Fig. 6, in the frequency domain,the vibrations are around the first resonant frequency of the long cantilever sting support system and have the largest magnitude,hence the vibration in pith plane is a low-frequency and big-amplitude vibration,and the response is mainly attributable to the first mode.Thus,the active vibration control system is proposed to dampen the first mode of the cantilever beam system.

During the vibration, the displacement y can be classified into static displacement y0and dynamic displacement y(t).Where, the dynamic displacement y(t) is undesirable and should be separated from y0as the control variable.Therefore,˙y= ˙y(t)is used as the feedback of closed loop active damping vibration control system. As the long cantilever sting support system vibrates upward, the dynamic bending moment M(t)excitated by the vector Fexc(t) progressively increases along the axial direction in pith plane,meanwhile the dynamic stress σ(t) and dynamic strain ε(t) gradually increases with the distance d from the neutral layer. It is noticeable that σ(t) and ε(t) are larger at the downstream in the long cantilever sting support system when the distance d under a certain value.Thus, the stackable piezoelectric actuators are set in stingroot to output forcef(t) and elongation ΔL(t) to counteract σ(t) and ε(t) based on the velocity feedback ˙y= ˙y(t). When the long cantilever sting support system vibrates downward,the system follows the same principle.

3.2. Modeling and analysis

As shown in Fig. 3, it is a cantilever beam system with active vibration control system.The complex cantilever beam system,assembled with aircraft model,balance and sting,makes it difficult to obtain the accurate theoretical mathematical model.Therefore, the vibration control problem is described based on the elastodynamics Finite Element Method (FEM) theory.

By discretization, the continuous elastic beam system is converted into a system with finite degrees of freedom. The dynamics model of the cantilever beam system with control can be described as

Fig. 3 Principle of active vibration control method.

Fig. 4 Vibration of a civil aircraft model lifting stepwise at Ma=0.6.

Fig. 5 Vibration of a civil aircraft model lifting stepwise at Ma=0.7.

Fig. 6 Spectral analysis of vibrations and long cantilever sting support system.

where M represents the global mass matrix, C the global damping matrix,K the global stiffness matrix.Fexc(t)is the global nodal load vector acting on the nodes of discrete elements.F(t)denotes the control force from sting-root embedded active damping device, y(t) represents the vibration displacement vector. M，C，K ∈Rn×n, Fexc， F， y ∈Rn×1.

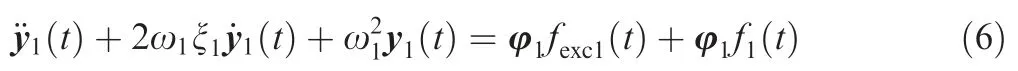
where fexc1(t)=Fexc(t), f1(t)=F(t). The four stackable piezoelectric actuators embedded in active damping device are divided into two equal groups. While aircraft model vibrates upward, suppose the control forces come from the two piezoelectric actuators above on the nodes j and k can be described as F(t)=[0···0 Fj(t) Fk(t) 0···0]T, and the stochastic dynamic force is Fexc(t)=[Fexc1(t) Fexc2(t) ··· Fexcn(t)]T. Then the first mode differential equation of motion in pitch plane can be expressed as20

where, φ1represents the first natural mode shape of the cantilever beam system, y1t( ) is the displacement response caused by the first mode,ω1denotes the first natural frequency and ξ1is the first mode damping ratio, φ1i， φ1j， φ1krepresent the ith element, jth element and kth element of first mode φ1,respectively.

Suppose the velocity sensor is installed on the mth node.The first mode differential equation of motion can be rewritten as

where y1mt( )represents the mth node's displacement of the first mode, φ1mis the mth element of the first mode shape.

The control force from each stackable piezoelectric actuator is defined as fs(t)=-Kv1m(t) based on velocity feedback,where Kvis the feedback coefficient. Let Fj(t)=fs(t)=-Kv1m(t), Fk(t)=fs(t)=-Kv1m(t), substituting them into Eq. (8) yields the closed-loop dynamic equation1m(t)+ 2ω1ξ1+φ1mφ1jKv+φ1mφ1kKv1m(t)

Since the cantilever beam system vibrates in the first mode,then φ1m,φ1jand φ1ksatisfy φ1mφ1j＞0,φ1mφ1k＞0.Thus,the control force provided by stackable piezoelectric actuators can be considered as a appending damping. In other words, the proposed vibration control method improves the damping of the long cantilever sting support system.

4. Control method

For the ideal condition in the laboratory or a certain wind tunnel testing condition with relatively stable dynamic force, the classical PD algorithm with a set of PD parameters can realize rapid and stable vibration control. While, in the wind tunnel tests in this paper, the angle-of-attack lifts stepwise from -4°to 10° and the airflow speed changes from Ma=0 to Ma=0.7.Hence the vibration is random and varies in a wide range,which can not be accurately described by mathematical models.A large amount of wind tunnel tests experience shows that several sets of PD parameters are needed to adapt various testing conditions, and a control method is need to adjust the PD parameters online. However, so far the division of testing conditions scope and the adjustment of PD parameters must rely on the expert experience and knowledge accumulated by experienced wind tunnel testers.It is the fuzzy control method that can better build control rules based on uncertain language variables according to the expert experience and knowledge than others.Therefore,in order to improve the ability to adapt to various complex testing conditions,a self-adaptive fuzzy PD control method is proposed,which is combined of classical PD control and fuzzy control.

As shown in Fig. 7, the self-adaptive fuzzy PD control method consists of two parts: the PD algorithm part and PD parameters self-tuning part based on fuzzy logic algorithm.In the PD algorithm,the velocity1m(t)is the measured output of active vibration closed loop control system, and we also define r(t), e(t) and u(t) as the value of vibration target, the output error,and the system input voltage,respectively.Then,the output error is defined as

The accelerometer is set on the mass center of aircraft model in pith plane to obtained velocity indirectly, and the vibration velocity can be expressed as

where ¨y1m(τ) is the mass center acceleration of the aircraft model, c is the response initial value of aircraft model's barycenter, it is an unknown constant quantity and ignored in the analysis.

PD algorithm control can be realized by applying the proportional and derivative of the output error e(t) on the stackable piezoelectric actuators through power amplifier,23the system input voltage is expressed as

where Kpand Kdare the proportional gain and derivative gain,respectively.

To realize control parameters adjustment automatically for various testing conditions, fuzzy logic algorithm is used to acquire proportional correction factor ΔKpand derivative correction factor ΔKdaccording to the velocity error Keand the velocity error rate Kec, and the proportional gain Kpand derivative gain Kdcan be respectively represent as

where Kp0and Kd0are the preset proportional gain and preset derivative gain, respectively.

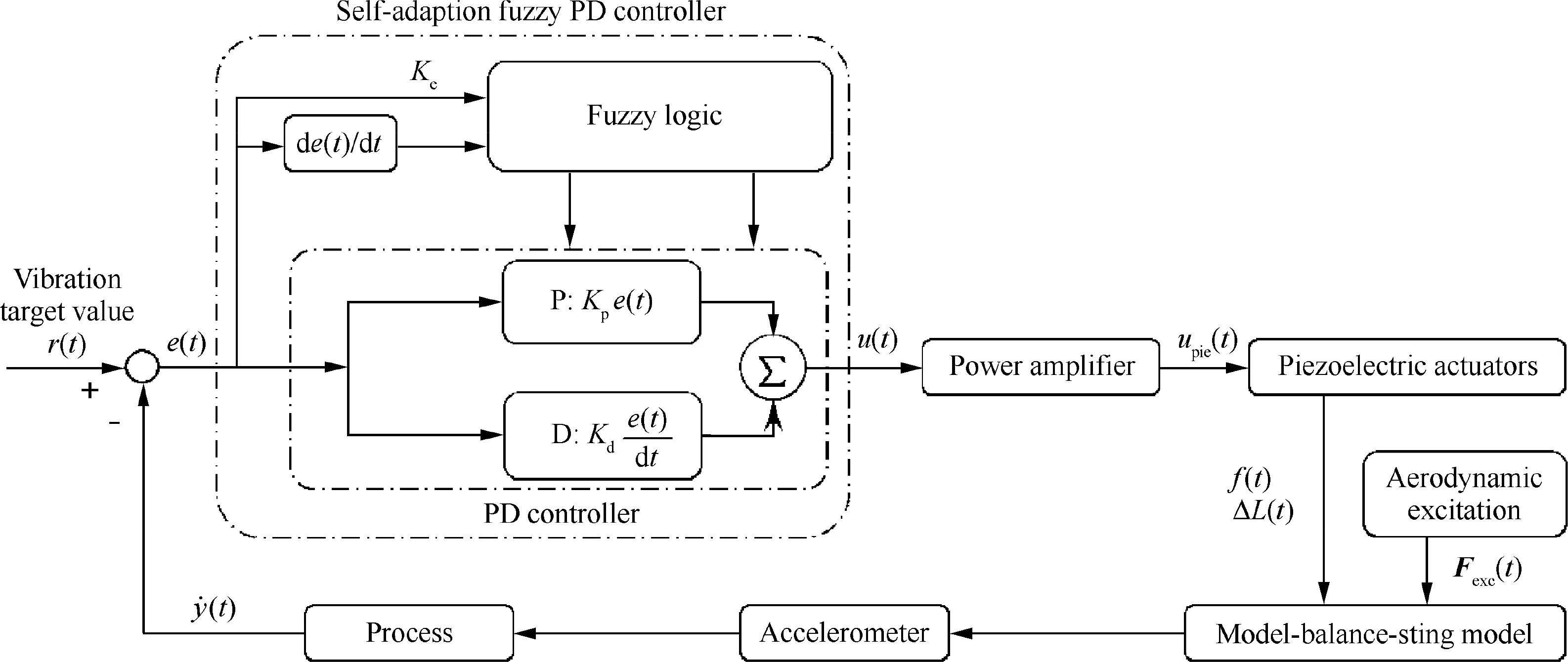
Fig. 7 Schematic of self-adaptive fuzzy PD control method.

In this paper, the fuzzy controller is set according to the angle-of-attack, the airflow speed and the performance of the wind tunnel through a series of wind tunnel tests, which relies on the expert experience and knowledge accumulated by experienced wind tunnel testers. The domains of velocity error Keand velocity error rate Kecare set to {0, 0.023, 0.045, 0.068,0.090, 0.113, 0.135, 0.158, 0.180} and {0, 0.281, 0.563, 0.844,1.125, 1.406, 1.688, 1.969, 2.250}, respectively. The domains of proportional correction factor ΔKpand derivative correction factor ΔKdare set to {0.20, 0.45, 0.70, 0.95, 1.20, 1.45,1.70, 1.95, 2.20} and {0.200, 0.325, 0.450, 0.575, 0.700, 0.825,0.950, 1.075, 1.200} respectively. The fuzzy sets of input Ke,input Kec, output ΔKpand output ΔKdare defined as {‘‘Positive Big”, ‘‘Positive Medium”, ‘‘Zero”, ‘‘Negative Medium”,‘‘Negative Big”},that is{NB,NM,ZO,PM,PB}.The Z membership function, the triangular membership function and the S membership function are chosen as membership functions.After experiment and adjustment, the fuzzy rules for ΔKpand ΔKdare built in Tables 1 and 2.

As the ultimate goal of the vibration control is to keep the aircraft model stable, the value of vibration target is r(t)=0.Then, the dynamic force f(t) supplied by stackable piezoelectric actuators through power amplifier can be described as

where npieis the number of stackable piezoelectric actuators,KAand Kpieare the amplification coefficient of power amplifier, and the load rigidity coefficient of stackable piezoelectric actuator, respectively.

Moreover, as shown in Fig. 8, to ensure the two groups of stackable piezoelectric actuators do not interfere with each other, one of the two groups stackable piezoelectric actuators work only in every half cycle.In one vibration cycle,when aircraft model vibrates above the equilibrium position in the first half cycle,the group of stackable piezoelectric actuators above works only. In turn, when aircraft model vibrates below the equilibrium position in the second half cycle, the group of stackable piezoelectric actuators below works only.

5. Verification testes in laboratory and wind tunnel

5.1. Experimental system

The verification tests for the active damping vibration control system focused on a civil aircraft model, the civil aircraft model is mounted on the long sting with sting-boot embedded active damping device. The active damping vibration control system is established and shown in Fig. 9.

To realize the velocity measurement of a real vibrating aircraft model in various testing conditions (ie. with dynamic strain gauge balance or not), accelerometer is selected to obtain aircraft's velocity indirectly. Moreover, the stochastic dynamic load is heavy and random, and the accelerometer should have wide dynamic range and high resolution.To avoid interference on test section flow around aerodynamic model and model's mass property, accelerometer with a light weight should be mounted inside the model.Therefore,the Integrated Electronics Piezo Electric (IEPE) accelerometer (PCB-SN-15267)is chosen,with the features of wide dynamic range,high resolution, small size and light weight.

The integration design of sting-root embedded active damping device mentioned in Section 2.2 contains 4 stackable piezoelectric actuators in two groups.After considering power requirements and small sting size, a sort of unwrapped stackable piezoelectric actuator is best chosen. Then corresponding configuration and pre-tightening mechanisms are designed.Photograph of sting-root embedded active damping device is shown in Fig. 10, and the main performance parameters of stackable piezoelectric actuator are shown in Table 3.

The controllers based on virtual instrument are designed as hardware part including acceleration collection module (NI PCI-4461 with 24 bit resolution), I/O modules (NI PCI-6528/5922),and host controller(PXIe-1082DC).Software part is developed by employing LABVIEW virtual instrument platform.The photograph of assembled control decision system is shown in Fig. 9.

5.2. Impulse tests in laboratory

The broadband stochastic dynamic load was simulated through hammering. The civil aircraft model was hammered in pitch plane with active damping vibration control system off and on, and the impulse response of the system are shown in time domain and frequency domain in Figs. 11 and 12.

As shown in Fig. 11, the first resonant vibration in pitch direction lasts for over 25 s without active damping vibration control system, whereas the vibration is damped within 0.75 s with the self-adaptive fuzzy PD control. Meanwhile,the damping ratio obtained by half-power improves from 0.0014 to 0.0296, and the damping ratio improves from 0.0083 to 0.0805 estimating from log decrement methods. As shown in Fig. 12, the long cantilever sting support system vibrates around the first resonant frequency and the peak is 0.76 g. Whereas, with the self-adaptive fuzzy PD control, the vibration at the first resonant frequency is well controlled and the peak is attenuated to 0.08 g. The spectral analysis of the impulse response shows an attenuation of 25 dB in the first resonant mode of 25.27 Hz.

Table 1 Fuzzy rules of ΔKp.

Table 2 Fuzzy rules of ΔKd.

Fig. 8 Working principle diagram of sting-boot embedded active damping device.

Fig. 9 Diagram of active damping vibration control system.

5.3. Stability testing

The stability of the active damping vibration control system has significant influence on the wind tunnel tests. Therefore,not only should the system guarantee a stable vibration control in one testing condition, it should also present stability in various testing condition. A load simulation method was used to test the stability of active damping vibration control system in laboratory. Several experiments were conducted in this paper.A series of stochastic dynamic loads were simulated to verify the stability of the system. Then, stability testing results of the system are shown and compared in Table 4 and Fig. 13,Tdmeans decrement time. It can be noticed that the vibration attenuates within 1.06 s whether the load is single stochastic dynamic load or continuous stochastic dynamic load, indicating excellent stability of the vibration control system.

Fig. 10 Photograph of sting-root embedded active damping device.

Table 3 Main performance parameters of stackable piezoelectric actuator.

Fig. 11 Impulse response in pith direction with active damping vibration control system ON & OFF.

Fig. 12 Spectral analysis of impulse response in pith direction.

Table 4 Stability testing.

Fig. 13 Stability testing in simulated testing conditions.

5.4. Wind tunnel verification tests

The civil aircraft model-balance-sting with embedded active damping device system was installed on the angle-of-attack adjusting mechanism in the continuous transonic wind tunnel.When subsonic and transonic tests were performed, the tail braced model-balance-sting system vibrated violently in pitch direction.Under the working conditions of angle-of-attack lifting stepwise at Ma=0.6 and Ma=0.7, the model vibrated from 5° angle-of-attack and 4° angle-of-attack, respectively.The vibrations represented by acceleration are shown in Figs. 14 and 15. Apparently, the vibration was too excessive to stop testing at 7°angle-of-attack,at Ma=0.6 and the maximum is 72 g.Furthermore,tests were stopped at 6.5°angle-ofattack, at Ma=0.7 and the maximum acceleration is 66 g.Besides, the aircraft model-balance-sting modes at Ma=0.6 and Ma=0.7 respectively are shown in Fig. 16 and Fig. 17.

Fig. 14 Vibration with active damping vibration control system OFF & ON lifting stepwise at Ma=0.6.

Fig. 15 Vibration with active damping vibration control system OFF & ON lifting stepwise at Ma=0.7.

To enable the key measurement equipment inside aircraft model to work normally, the vibration should be less than 5 g,apparently the low-frequency and big-amplitude vibration has a great influence on the normal performance of key measurement equipment,leading to data error or data corruption,or to be more serious,the support system is destroyed and the safety of wind tunnel test will suffer the serious threat.

As shown in Figs. 18 and 19, wind tunnel verification tests were performed at normal pressure/temperature condition in a continuous transonic wind tunnel.

The verification tests performed in wind tunnel were conducted under the working conditions of angle-of-attack α lifting stepwise at Ma=0.6. During the tests, the dynamic data of angle-of-attack α and acceleration ¨y1m(τ)changing relationship over angle-of-attack α are obtained. As shown in Fig.14,compared with the wind tunnel test without active damping vibration control system,aircraft model does not vibrate obviously at 5° angle-of-attack, the useable angle-of-attack breaches 10° and reaches 11°. By contrast, the number of useable angle-of-attack has increased by 7°. The acceleration¨y1m(τ) value reach the maximum of about 1.73 g at α=11°,reducing by 73.27 g to 2.31% of previous acceleration value at α=7°. The spectral analysis is shown in Fig. 16, the first resonant mode is 25.1 Hz and an attenuation of 60 dB is shown.

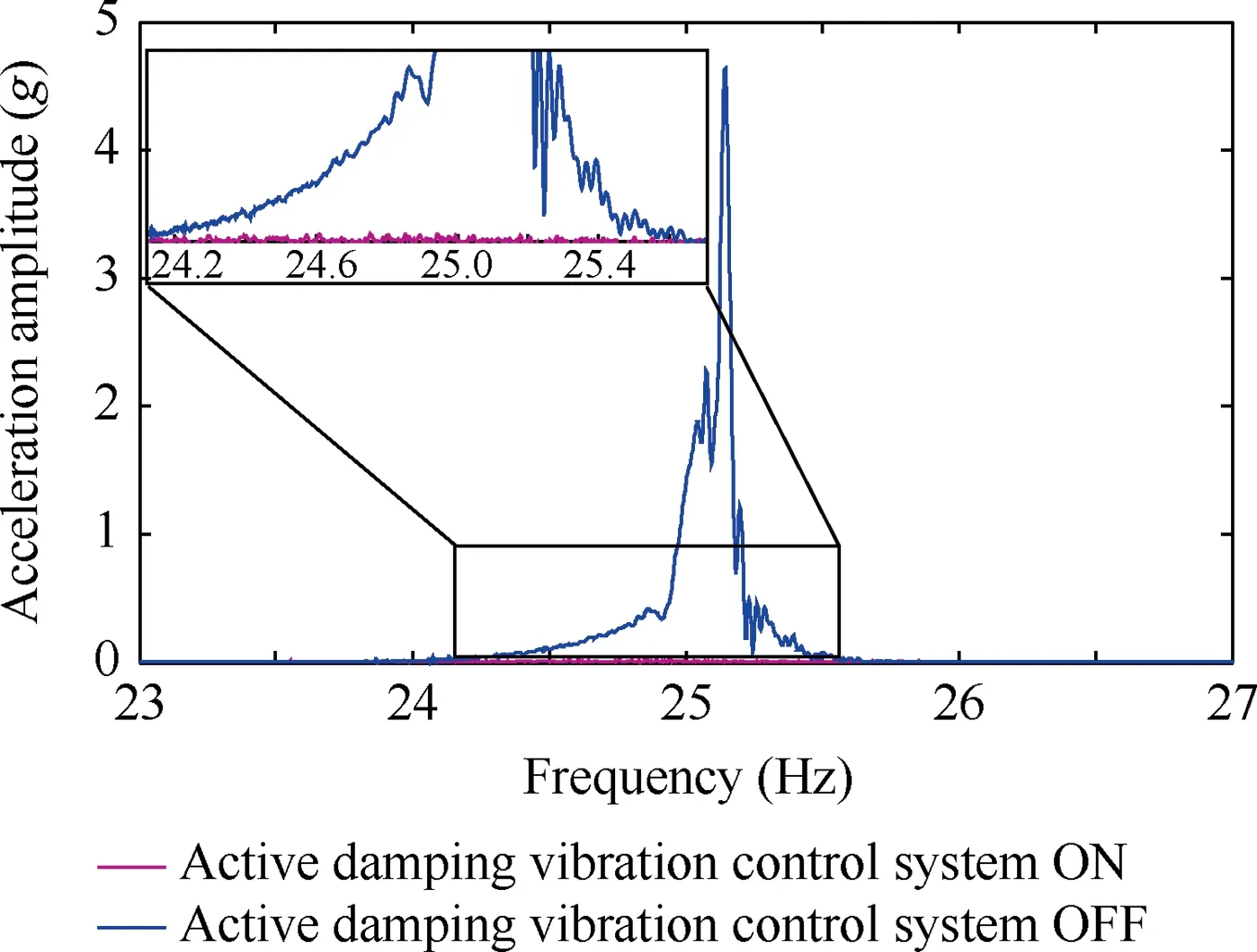
Fig. 16 Spectral analysis of vibration at Ma=0.6.

Fig. 17 Spectral analysis of vibration at Ma=0.7.

Fig. 18 Photograph of experimental system installed inside test section without control decision system.

Fig. 19 Photograph of verification tests performed in a continuous transonic wind tunnel.

Similarly,a series of verification tests were conducted under the working conditions of angle-of-attack α lifting stepwise at Ma=0.7. As shown in Fig. 15, compared with the wind tunnel test without active damping vibration control system, aircraft model does not vibrate at 4°, the useable angle-ofattack reaches 8° and the aircraft model starts vibrating seriously when angle-of-attack just arrives 9°. By contrast, the number of useable angle-of-attack has increased by 5°. Theacceleration ¨y1m(τ)value reach the maximum of about 1.2 g at α=6°, reducing by 66.8 g to 1.76% of previous acceleration value at α=6.5°.The spectral analysis of vibration is shown in Fig. 17, the first resonant mode is 25.1 Hz and an attenuation of 24 dB is shown. The damping ratio obtained by halfpower improves from 0.0008 to 0.0046.

Table 5 Test results.

Based on the impulse tests conducted in laboratory and verification tests performed in a continuous transonic wind tunnel above, the results are gathered and shown in Table 5.

The aircraft model does not vibrate from -4° to 11° at Ma=0.6,and at Ma=0.7,the aircraft model starts vibrating seriously when angle-of-attack just arrives 9°. The number of useable angle-of-attack has increased by 7° at Ma=0.6 and 5° at Ma=0.7 respectively. Meanwhile, the spectral analysis shows attenuations of 60 dB at Ma=0.6 and 24 dB at Ma=0.7 in the first resonant modes.At Ma=0.7,the damping ratio obtained by half-power improves from 0.0008 to 0.0046.Consequently,the damping ability resisting the aerodynamic excitation is strengthened,satisfying the requirements of practical wind tunnel tests. Besides, the maximum of remainder acceleration is less than 5 g, the key measurement equipment inside aircraft model can work normally.

6. Conclusions

(1) In this paper, an active damping vibration control system based on piezoelectric actuator and velocity feedback using accelerometer, is proposed for reducing the vibration of aircraft model in a continuous transonic wind tunnel,solving problems caused by flow separation and turbulence during wind tunnel tests. A sting-root embedded active damping device with four piezoelectric actuators in two groups was designed to ensure power requirements.(2) Moreover, the system is modeled and analyzed according to dynamic theory, meanwhile, the coefficients associated with damping are deduced to evaluate the property improvement of system itself. Then, a selfadaptive fuzzy PD control method is proposed to realize control parameters adjustment automatically for various testing conditions.(3) A series of verification tests were performed in laboratory and a continuous transonic wind tunnel, the feasibility, stability and performance were verified, which indicates the proposed active damping vibration control method and system can meet the requirement of wind tunnel tests. Our further researches will focus on the fuzzy control method with the ability of self-learning or self-organizing and the active damping vibration control of multi-dimensional vibration, especially both in pith and yaw directions.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (Nos. 51622501 and 51621064) and the high-level personnel innovation support program of Dalian(No. 2017RJ04).