应用数学思想，提升解题能力

江苏省淮阴中学教育集团新淮高级中学 张 艳

高中数学的学习已经到了一个较为深入的阶段，学生解决问题的方法已不再局限于一个萝卜一个坑，而更多地在于将数学思想和数学方法进行组合应用，解决难题。因此，对学生来说，数学思想的掌握是非常重要的，其中，基础的函数思想、方程思想和不等式思想是最容易被大家忽略的。接下来，我会将这几种数学思想的具体用法与大家分享。

一、函数思想，实现转化

函数的表示方法是多种多样的，包括解析法、图像法和列表法。通过这些表示方法，我们可以实现数字与图像之间的转化。因此，应用函数思想，可以简洁迅速地解决很多复杂的问题。

数学题的解法并不是唯一的，但是一定有最优解。通过函数思想，实现代数式与图像之间的转化，往往能够简化运算，使结果更加明了。如综合题：求函数f(x)=x-cosx在实数R内零点个数及所在区间[m,m+1]。一开始，大家会认为这是一道纯计算的问题，打算用求导的方法来解决：首先对函数进行求导得f’(x)=1+sinx≥0，那么函数f(x)在实数范围内单调递增；当x趋于负无穷时，f(x)＜0，当x趋于正无穷时，f(x)＞0，因此函数f(x)在实数范围内的有且仅有一个零点。接下来关于零点范围[m,m+1]的问题就很难解决了，只能通过二分法不断计算，同时，中间还涉及余弦值，困难可想而知。所以，综合考虑下来，这道题不适合用求导的方法来解决。因此我们可以考虑通过函数思想来解决，需要求f(x)=x-cosx的零点，相当于求函数y=x和y=cosx的图像在实数R上的交点个数和范围。那我们画一个平面直角坐标系，分别将函数y=x和y=cosx的图像表示出来，结果是非常清晰的：两图像仅有一个交点，交点范围为[0,1]。

代数式是抽象的，在解决问题过程中有很大的局限性。因此，通过函数表达形式的多样性，可以实现代数式与函数图像的转化，从而将抽象内容直观化。事实证明，数形结合方法在很多数学题中都有很大的优势。

二、方程思想，动中求静

根据解的范围求方程中参数的问题是比较复杂的，因为仅知道范围，但中间的可能情况却非常多。根据方程思想，我们可以对宏观条件进行分析，找到共同特征，实现动中求静，最终解决问题。

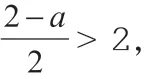
显然，方程的根的问题是不断变化、非常复杂的，但是通过方程思想，我们将条件拆解进行总体分析，就能够得到共同特征，从而进行求解。通过这种方法，我们可以实现动中求静，简化计算。

三、不等式思想，探析数量关系

不等式问题的存在形式非常广泛，很多时候是和函数相结合的，函数的定义域和值域就是不等式存在的最佳形式。因此，教师一定要培养学生洞察条件的能力，可以从隐藏条件中寻求突破口，从而探析其中的数量关系。

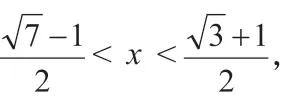
通过不等式思想，我们可以实现代数式与函数之间的转化，其中的取值范围问题也可以轻松地转化为函数的定义域和值域。通过这样的转化，学生在探析其数量关系方面的解题能力可得到大大提升。

初中阶段的很多考点会变成高中阶段的解题工具。因此，希望大家认真思考函数思想、方程思想和不等式思想的适用范围和具体用法，同时也可以在学习过程中自行总结，让这些思想为解题献力。