基于Choquet积分的直觉模糊联盟合作博弈的Shapley值

南江霞， 关 晶， 王盼盼

(桂林电子科技大学 数学与计算科学学院，广西高校数据分析与计算重点实验室，广西 桂林 541004 )

0 引言

1974年，Aubin[1]首次提出了模糊联盟的概念，即参与人在参加合作时，参加程度可以用[0,1]间中的一个实数表示。因其更能反映现实问题和更符合人们的心理，使得模糊联盟合作博弈的理论及应用引起了学者们的关注。进而研究者们对模糊联盟合作博弈进行了深入的研究[2～8]。但模糊集的单一隶属度仅能表示参与人“参加”、“不参加”联盟两种程度，而无法表示参与人因环境和条件的不确定性及信息的不完全性，同时也涉及到经济、政治、心理行为和意识形态等复杂因素的影响是否参加联盟时存在一定的犹豫程度。为此，Atanassov[9,10]提出的直觉模糊集可以有效地描述合作博弈中参与人的肯定、否定和犹豫三种状态信息。因此，直觉模糊集能更好地表示合作博弈中的不确定信息。目前关于直觉模糊集合作博弈相关研究的文献较为匮乏。仅有Mielcová[11]研究了直觉模糊集作为特征函数的n人可转移效用直觉模糊博弈期望核心。高作峰、郭菊花[12]探讨了特征函数是直觉模糊集的合作博弈的核心、核仁和τ值。 韩婷和李登峰[13]探究了直觉模糊联盟合作博弈的Shapley值求解方法，文献[13]利用区间Choquet积分得到直觉模糊联盟合作博弈的特征函数为区间数，再利用COWA算子将区间特征函数集结为实数，从而将直觉模糊联盟合作博弈Shapley值的计算转化为经典合作博弈Shapley值。从逻辑上讲，合作博弈的特征函数为区间数，其Shapley值也应为区间数，然而文献[13]得到的直觉模糊联盟合作博弈的Shapley值是实数。为此，本文进一步研究直觉模糊联盟合作博弈的Shapley值，拓展文献[14]模糊联盟合作博弈的Shapley值的计算方法，我们得到的直觉模糊联盟合作博弈的Shapley值为一个区间数，并避免了区间数的减法，进一步证明了本文提出的直觉模糊联盟合作博弈Shapley值满足经典合作博弈Shapley值的公理性。最后通过数值实例说明本文提出的直觉模糊合作博弈Shapley值的合理性、有效性和优越性。

1 预备知识

1.1 直觉模糊集与直觉模糊联盟

Atanassov首次提出直觉模糊集的定义如下：

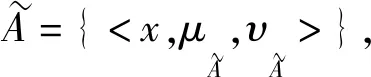
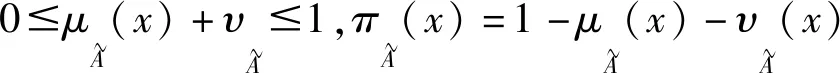
直觉模糊联盟就是参与人集合上的直觉模糊集子集，它描述了参与人对联盟的参加程度、不参加程度和犹豫程度。直觉模糊联盟是模糊联盟的拓展，模糊联盟是直觉模糊联盟特殊情况。

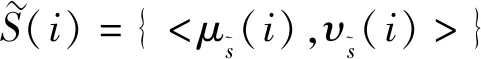
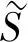
1.2 区间Choquet积分

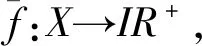
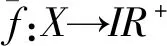
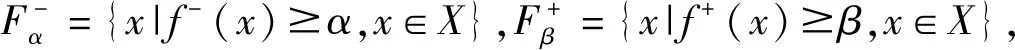
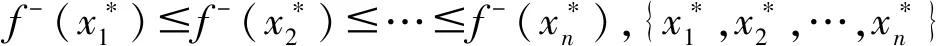
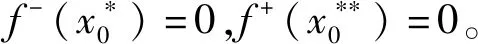
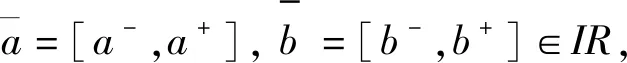
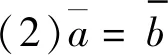
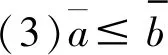
1.3 经典合作博弈Shapley值

经典合作博弈可以表示为一个序对，其中N={1,2,…,n}为参与人集合，P(N)是N的幂集，v为n人合作博弈的特征函数，即v:P(N)→R，其中R为全体实数集，v(φ)=0。

定义5在合作博弈中，存在唯一的函数φi(v):P(N)→R

(1)

满足

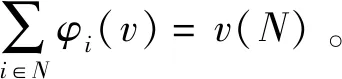
公理2(对称性)若参与人i,j∈N对任意联盟S∈P(N{i,j})，都有v(S∪{i})=v(S∪{j})，则φi(v)=φj(v)。

公理3(可加性)对任意两个合作博弈和，如果存在一个合作博弈，对任意联盟S∈P(N)，总有(v1+v2)(S)=v1(S)+v2(S)，则φi(v1+v2)=φi(v1)+φi(v2)。

公理4(哑元性)若对所有包含参与人i的联盟S，都有v(S)=v(S{i})，则φi(v)=0。因此，称φi(v)为Shapley值。

2 具有区间Choquet积分的直觉模糊联盟合作博弈的特征函数及性质

(2)

其中

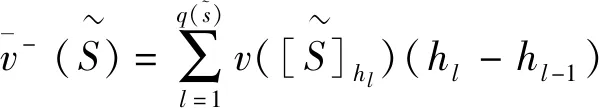
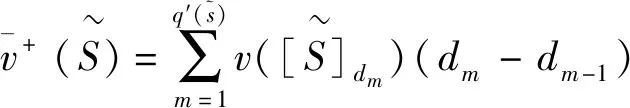
可以证明式(2)得出的直觉模糊联盟合作博弈的区间特征函数满足经典合作博弈特征函数的一些性质。

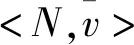
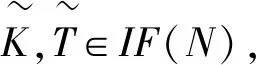
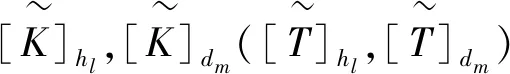
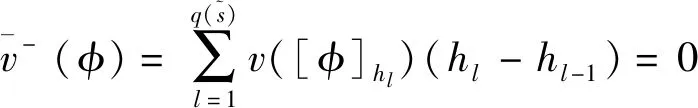
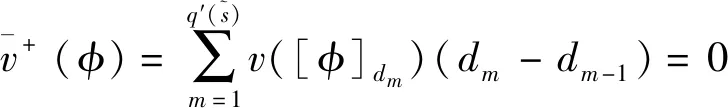
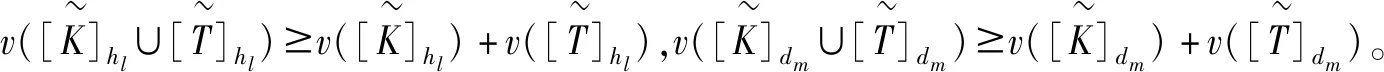
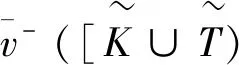
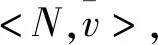
由性质1证明，性质2易证。

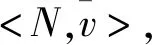
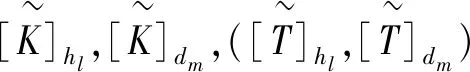
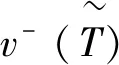
同理可得

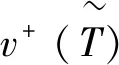
3 具有Choquet积分的直觉模糊联盟Shapley值及性质

由式(2)可知，具有Choquet积分形式的直觉模糊联盟合作博弈的特征函数为区间数，为了避免区间数的减法，我们拓展了文献[14]具有模糊Choquet积分的模糊联盟合作博弈的Shapley值的计算方法，给出具有区间Choquet积分的直觉模糊联盟合作博弈的Shapley值定义。

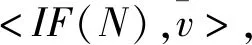
(3)

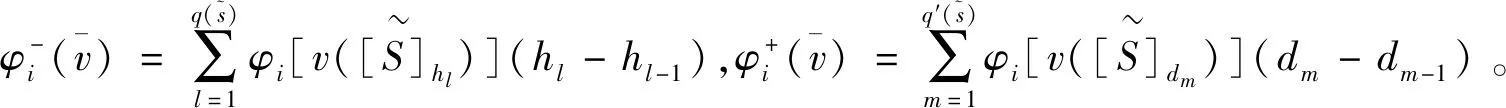
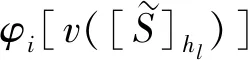
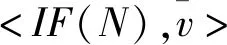
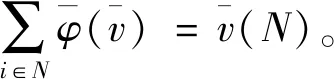
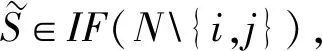
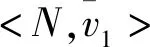
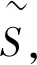
证明公理1(有效性),由经典Shapley值有效性可得

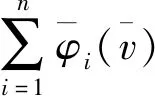
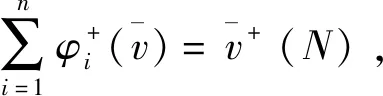
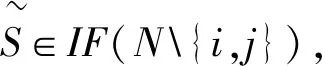
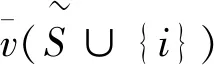
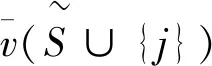
进而有

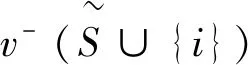
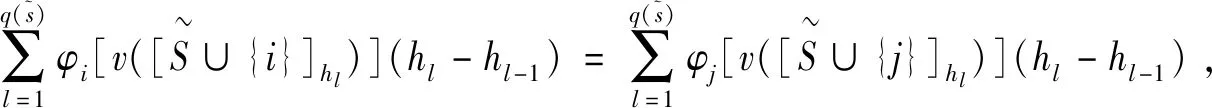
由经典Shapley值可加性及式(2)可得

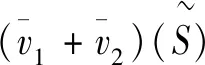
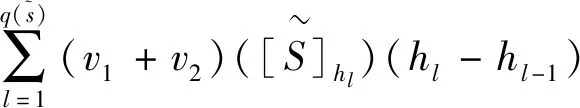
因此有

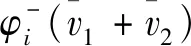
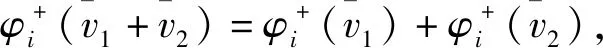
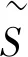
由经典Shapley值哑元性及式(2)可得

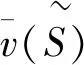
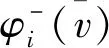
=0

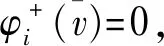
4 数值实例分析

假设有甲，乙，丙三个药商(分别代表1，2，3参与人)如果完全参与到一个种药的研发时，联盟的收益值如下(单位：万元)

v({1})=100,v({2})=200,v({3})=200,v({1,2})=600

v({1,3})=600,v({2,3})=800,v({1,2,3})=1200

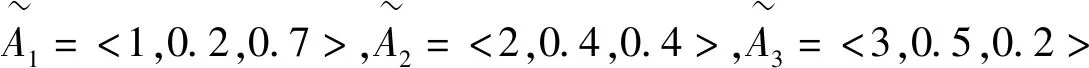
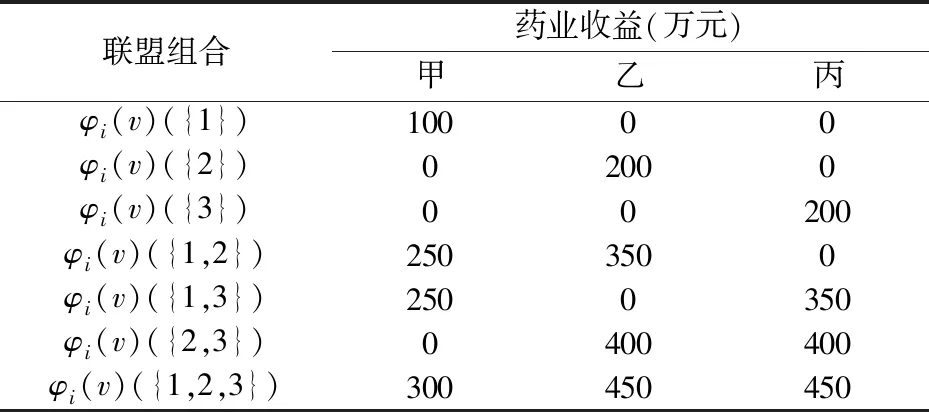
表1 清晰联盟下的收益分配

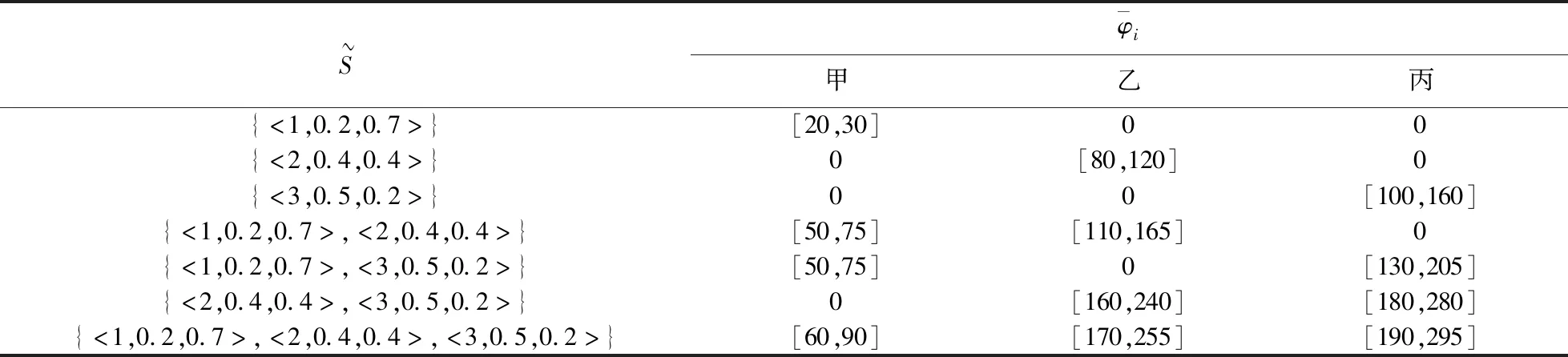
表2 直觉模糊联盟下收益分配

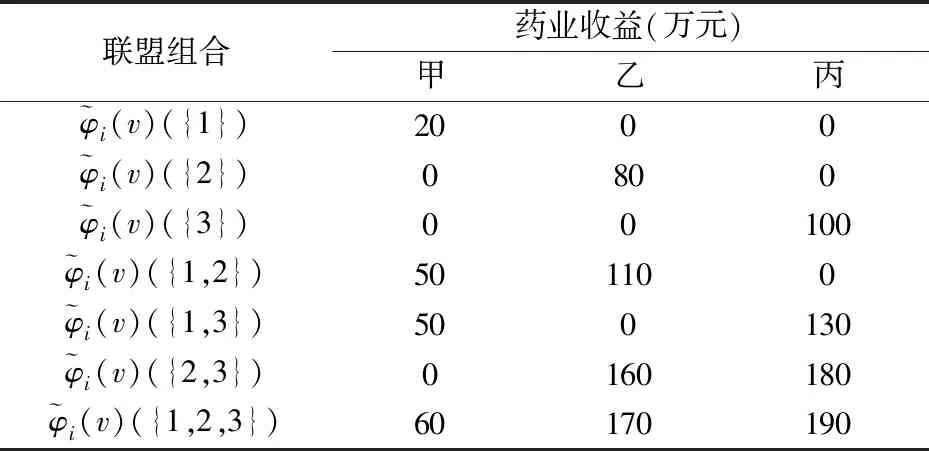
表3 模糊联盟合作博弈的收益分配

由表2和表3可得，模糊联盟下的收益分配值是直觉模糊联盟下收益分配值的左端点值。因此，直觉模糊联盟Shapley值是模糊联盟Shapley值的推广。

5 结论

本文是将模糊联盟合作博弈拓展到直觉模糊联盟合作博弈，给出了带有区间Choquet积分的直觉模糊联盟合作博弈的Shapley值的求解公式，并证明其满足经典Shapley值的公理性，即有效性公理、对称性公理、可加性公理和哑元性公理。本文先求出清晰联盟合作博弈的Shapley值，再求出带有区间Choquet积分的直觉模糊联盟合作博弈Shapley值，其优点是避免了先用Choquet积分集结特征函数再求Shapley值的过程中遇到区间数的减法，进而简化了计算量。