考虑预付定金和退货的SMPEs产品定价与优化策略
2019-10-24程明宝张弓亮
程 硕, 曹 铭, 程明宝, 张弓亮
(1.仲恺农业工程学院 管理学院,广东 广州 510230; 2.广东金融学院 经济贸易学院,广东 广州 510521; 3.广东工业大学 管理学院,广东 广州 510520)
0 引言
在互联网经济高速发展的时代,各经济主体的决策、交易等行为越来越多地依赖信息网络,但由于当前经济下行压力加大,制造业尤其是中小制造型企业(SMPEs)增长严重缺乏动力,想要从困境中突围,除了加大R&D投入,更要注重利用互联网经济进行营销和推广。互联网下信息传播速度快、广度大、成本低等特点,能够形成规模效应,对SMPEs的产品推广、销售、售后以及迅速回笼资金、降低风险等方面均有促进作用[1]。如何有效的利用网络技术提高制造型企业的生产效率、降低产品生产成本、增强企业的核心竞争力,有机的耦合“互联网+”和SMPEs之间的关系,运用互联网思维完成对产业的改造和升级,成为传统制造业发展和突破的关键所在。较多B2B/B2C企业都通过利用互联网的手段,通过采取“OEM生产”、“网络营销”、“网上预付订购”等策略[2],取得了巨大的成果。例如今年“双十一”中苹果、小米等多家电子产品生产商,均采用产品预售预付定金给与相应价格折扣的方法,刺激消费者的购买行为,降低市场需求不确定性所带来的风险,进而提高产品销售带来的收益[3]。但是由于商品是在线销售,顾客只能在商品配送完成后才能接触到商品,就会出现因商品达不到顾客的个性化要求而出现退货[4]。但是,当顾客的退货成为大概率事件时,如何协调顾客退货与产品定价和生产策略之间的关系,成为目前互联网时代下SMPEs十分关注的热点问题。
近年来,很多学者对退货问题进行了研究,对于线上销售环境下的退货机制与退货策略的研究较为突出。为清晰的展示相关文献的研究成果,文献主要研究内容整理如表1所示。Vlachos等[5]专门针对电子商务中的退货问题,对邮购、网上购物或电子商务中发生的退货进行分类处理,通过建立随机市场需求下单周期产品的订货决策模型,得到不同情形下的最优订货策略;Huang等[6]研究了二级供应链(单一供应商和多零售商)下的退货与供应协调问题,通过分析和数值算例验证了该条件下的最优产品库存水平;Li等[7]运用禁忌搜索算法研究存在产品退货和再制造情况下的动态批量问题,针对此类NP-hard问题,设计了环链状的生产/再生产结构,并通过TB算法得出成本约束条件下的最优批量;Liu等[8]在前人研究的基础上,研究了存在顾客退货需求与退款有关情况下的供应链协调问题,构建了以退款金额为决策变量的供应链利润最大化模型,设计了需求不确定的情况下供应链的回购契约,分析验证了该模型的利润最大化下的最优退款金额;Radhi和Zhang[9]进一步分析探讨双渠道下退货问题,研究同渠道和跨渠道退货模式下的零售商产品定价模型,得出集中式和分散式决策模式下零售商最优产品定价策略。上述文献均是考虑了存在顾客退货的背景下分析研究了单因素决策问题,反映出退货现象是一个不可忽视的重要问题。对顾客的意愿的重视增加了销售的难度,尤其是在当前信息较为“透明”环境下,消费者在决策时会更为“聪明”,商品的性价比会直接的影响商品的退货概率,退货又会对生产商和销售商造成一定程度负面影响。因此对电商环境下的供应链退货分析的研究有着现实意义。

表1 相关文献综述
也较多学者进一步分析存在退货情况下多因素决策问题。Chen和Bell[10]研究了顾客退货情况下零售企业的定价和订货策略,给出了加法模式的随机需求下的最优零售价格和最优订货量;Özer等[11]对存在退货和不退货两种销售途径市场条件下,考虑需求关于价格敏感、顾客行为和渠道盈利性等多因素,构建交货期时间、产品定价和生产量多决策变量的利润最大化模型,通过分析得出决策变量与企业利润及企业产品销售策略之间的关系;李健等[12]分析了顾客有限理性退货下的两阶段C2B模式的回购策略,通过调节退货后的制造商回购价格实现两阶段销售协调;Flapper等[13]研究了顾客退货信息影响下的生产库存系统优化问题,其中退货的需求和退货信息服从Poisson分布,退货信息包括实际退货和取消退货两种情况,运用一个Markov决策过程构建信息对称和信息不对称情况下的最优生产量-价格折扣模型;樊双蛟和王旭坪[14]通过构建退货再次销售的库存模型,对商品定价和订货量进行联合决策分析,给出最优解存在的条件并给出求解方法;陈敬贤和梁樑[15]以Hotelling模型为基础,利用产品匹配概率刻画顾客的退货行为,分析了存在顾客退货下的产品定价和产品定位决策问题。上述文献中考虑退货均只是与市场需求或产品销售量有关,考虑条件较为单一,与实际可能存在些许偏差。而现实中,消费者的无缺陷退货主要是由于产品价值与消费者的需求偏好存在差异。本文在考虑存在多类顾客不同退货概率和直销商采用“预付款+价格折扣”销售模式的情况下,研究商品退货量是确定型和随机型(与市场需求、产品销售量和产品折扣有相关性条件下)下直销商的产品定价和产品折扣策略决策。
在目前电商行业不断壮大的情况下,网购日益普遍,几乎所有的网购平台和第三方支付软件均是向侧重维护消费者的利益进行倾斜,消费者可以随时进行商品下单购买、随时随地的进行撤单退货,这就会给制造商和销售商带来相应的损失。面对此类情况,不同的线上销售商会采用不同的销售策略,关于预付定金方面的研究,Maiti等[16]研究了产品定价受需求和预付款影响、交货期时间随机条件下的产品库存系统优化问题,通过设计GA算法证明了批发商的预付策略对其库存系统有着正面积极的影响作用;Thangam[17]对存在预付折扣和商业信用的三级供应链库存系统EOQ模型进行研究,并通过模型推导和数值证明得出供应链中最优价格折扣和订货批量策略;王文利和骆建文[18]研究了预付款模式下二级供应链的最优生产和融资决策问题,并分析了供应商的自有资金、价格折扣两种因素对供应链融资绩效的影响;李超和骆建文[19]建立供应链存在资金约束的动态博弈模型,分析了预付款对资金约束下的供应链效率的改进效果,通过设计零售商预付款的收益共享协调机制,实现供应链利益最大化;Taleizadeh[20]和Tavakoli[21]分析了存在零售商退货情形下,采用支付预付款方式的零售商最优批量决策问题,通过设计算法和数值算例进行了验证,并设计一种基于预付款的库存控制系统,实现模型和研究结果解决实际问题。基于对预付定金问题的分析,本文研究中的直销商采用“预付款+价格折扣”销售模式,采用其中比较普遍的一种模式:顾客先预付一部分定金,在线上进行下单购买商品,此时线上销售商会在顾客确定收货后,给与顾客相应的折扣;但是如果预付定金的顾客最终选择退货或没有购买该商品,则不退还定金。
基于对以上文献的阅读,在前人的研究基础上,本文针对生产商网上直销模式下的单周期的单一生产商、多类顾客的二级供应链,分别研究市场需求确定和不确定两种情况下,存在顾客可预付定金和产品可退货的生产商产品定价及优化策略问题。并在此基础上,针对多类不同顾客预付定金比例、产品退货数量均是关于产品折扣系数敏感的情况下,采用拉格朗日乘子法对模型解的最优性进行讨论和分析,进一步研究生产商产品定价和产品价格折扣的协调策略。
1 问题描述
考虑某一生产商生产并网上直销一种产品,市场需求Q是关于价格p的随机函数,由于产品销售的特性,可接受预付订单产品款项,并存在顾客产品退货行为。其中,市场存在两类顾客,即A类为提交预付定金的顾客,B类则为不预付定金的顾客。企业为了减少产品销售中存在的风险,尽量的鼓励顾客预付定金,会给与A类顾客一定的价格折扣。同时,两类顾客若对该产品不满意,可进行退货。但A类顾客退货,不返还其预付定金,B类顾客退货返还货款。AB两类顾客退货的产品不进行二次售卖,若期末销售产品剩余,则转换为相应的产品残值;若存在缺货现象,则生产商进行外部采购满足顾客需求。
p:产品的单位售价;p0:为不考虑预付定金销售模式的产品价格;w:产品的单位生产成本;s:期末未销售产品的单位残值;v:为单位产品的外包成本;其中存在关系式:p>w>s。
Q:产品的市场需求,且Q=D(p)=kp-ε(K>0,ε>1),本文考虑的产品是关于价格弹性的商品[22],例如一些畅销品、可替代品等一般都是价格弹性较大的产品;
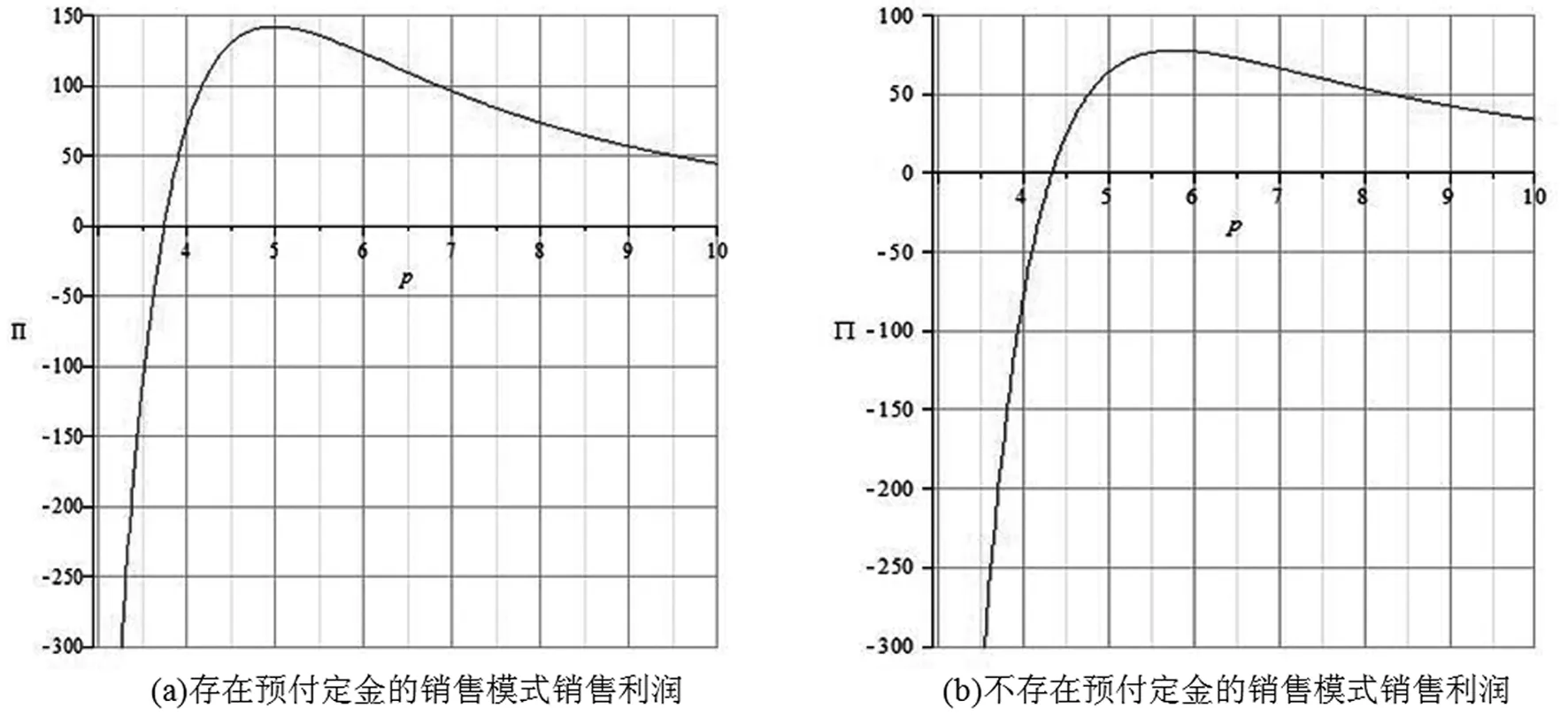
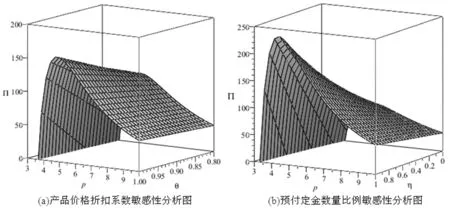
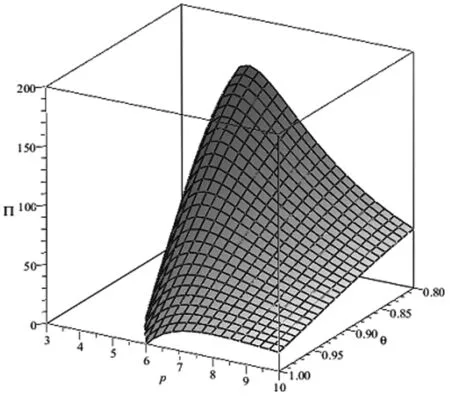
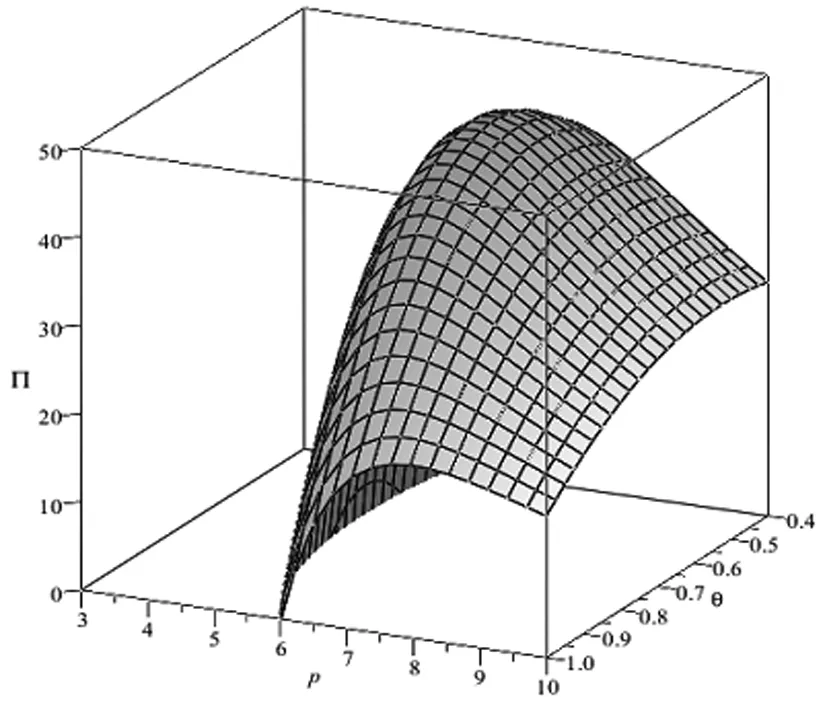
ηD(p):为预付定金的产品数量,其中0<η<1;则假设预付定金的顾客中最终购买该产品的产品数量为aηD(p),其中0 (1-η)D(p):为不预付定金的产品数量,则假设该类顾客中,最终购买该产品的数量为b(1-η)D(p),其中0 rp:为预付单位产品的定金,其中0 θp:为给与预付定金的顾客优惠折扣后的单位产品价格,θ为折扣系数,0<θ<1; 该种商品的购买和退货遵循以下原则: (1)预付定金的顾客可享受价格优惠,但该类顾客若退货,则定金不返还,其余货款返还; (2)不预付定金的顾客不享受产品价格优惠,但该类顾客退货,返还全部货款; (3)预付定金的顾客中最终退货的产品所占的比例小于不预付定金的顾客中最终退货产品的所占的比例,即a>b。 (a)考虑不存在预付定金的销售模式 为了更为明显的对比是否预付定金两种不同的销售模式对制造企业的影响,现对不存在预付定金的销售模式进行研究。在不预付定金的情况中,顾客则全部按B类顾客(不预付定金类型)计算,则该种销售模式的产品利润函数Π0(p0)可表示为: Π0(p0)=p0×bD(p0)+s×(1-b)D(p0)-wD(p0) (1) 对公式(4)对价格p0进行一阶求导,可得: (b)考虑存在预付定金的销售模式 假设生产商企业的生产量为X,若X=D(p),则在某单销售周期内,此四类顾客的产品销售收入如表1所示。其中,A类顾客最终购买的产品数量为aηD(p),因A类顾客预付定金,制造商企业会给予A类顾客相应的价格折扣θp,则制造商企业在A类顾客方面最终获得的产品销售收入则为(θp)×aηD(p);对于A类顾客中最终退货的顾客,制造商企业会选择不返还顾客预先交付的定金,同时,会将这部分退货的产品(1-a)ηD(p)做残值的处理,则这时的相应收入为(rp+s)×(1-a)ηD(p);对于B类顾客中最终选择购买的产品数量为b(1-η)D(p),因B类顾客没有预付定金,则产品的价格是没有相应优惠的,则这部分产品的销售收入为p×b(1-η)D(p);对应的B类顾客中最终选择退货的这部分产品,该部分的产品需全额退款,其收入为s×(1-b)(1-η)D(p)。 表1 不同情况下的产品销售收入分布表 该生产商企业单销售周期的利润收入模型为: Π(p)=(θp)×aηD(p)+(rp+s)×(1-a)ηD(p)+ p×b(1-η)D(p)+s×(1-b)(1-η)D(p)-wD(p) (2) 定理1在市场需求确定的情况下,存在最优的产品销售价格p*,使得制造商产品销售利润达到最大值Π(p*),其中 证明分别对Π(p)进行一阶求导和二阶求导,存在最优解的一阶条件和二阶条件如下 (ε/p)[s×(1-a)η+s×(1-b)(1-η)-w]} (3) (4) X*=D(p*)=K(p*)-ε(其中,K>0,ε>1) Π(p*)=(θp*)×aηD(p*)+(rp*+s)×(1-a)ηD(p*)+ p*×b(1-η)D(p*)+s×(1-b)(1-η)D(p*)-wD(p*) 定理1表明在市场需求确定的情况下,消费者是否采用预付定金方式以及产品退货率都会对制造商的产品定价和总收益有很大的影响。作为决策的制定者,在制定最优的产品定价决策时要充分考虑到消费者中采用预付定金的数量比例以及产品退货率,然后再根据自身特性进行决策。 对上述预付定金和不预付定金的两种销售模式进行比较,可得两种销售模式利润之差M(p): M(p)=Π(p)-Π0(p) ={(θp)×aηD(p)+[rp×(1-a)ηD(p)+ s×(1-a)ηD(p)]+p×b(1-η)D(p)+ s×(1-b)(1-η)D(p)-wD(p)}- {p×bD(p)+s×(1-b)D(p)-wD(p)} =[(θa-b)p+s×(b-a)+rp×(1-a)]ηD(p) (5) 若M(p)>0时,则Π(p)>Π0(p),由(5)式推导可得:[(θ-r)p-s]a>(b-r)p-sb,则分析推导可得定理2。 单生产周期内,若该产品的市场需求量随机,假设市场需求量Q=σD(p),其中σ是定义取值范围为[A,+∞)上的随机变量(A>0),其均值为μ(其中μ≥1),f(σ)和F(σ)分别是概率密度函数和分布函数。将市场产品的需求量Q和企业的实际生产量X进行分段讨论分析。 当X ①若0 ②若ηQ (6) 上式可转换为: maxE[Π(p)]=[θp×aη+p×b(1-η)+rp×(1-a)η-w]D(p)μ- (7) (8) (9) (10) (11) 对需求随机情况下的退货方程(公式(11))可转换为: E[Ω(g,p)]=(1-b)(μ-Λ(g))+(b-a)(μ-Υ(g)) (12) 则将(8)~(10)式和(12)式代入(7)式可得: maxE[Π(p)]=[θp×aη+p×b(1-η)+rp×(1-a)η-w]μD(p)-(p-s)× D(p)Ω(g,p)-(w-s)×D(p)Γ(g)-(p+v-w)×D(p)Λ(g)-rp×D(p)Υ(g) (13) 假设(13)式中[θp×aη+b(1-η)+r×(1-a)η]=M,则对(13)式中总利润关于价格p的一阶导数为: [D(p)+(p-s)×D′(p)]Ω(g,p)-(w-s)[D′(p)Γ(g)]- [D(p)+(p+v-w)D′(p)]Λ(g)- [D(p)+p×D′(p)]rΥ(g) +(p+v-w)×Λ′(g)+rp×Υ′(g)} (14) 另外,假若Q=σD(p)中的σ=1,则可以把确定性问题看作是随机性问题的一个特例,即在生产商生产的产品存在X≠Q情况时,此时生产商的产品最优生产量X满足以下条件 除了上述针对市场需求确定型和随机型两种情况的考虑外,本文考虑了一种更为贴近市场实际的需求情况:市场需求中顾客预付定金产品的数量比例(η)、预付定金的比例(r)、产品销售数量比例(a和b)均是关于生产商产品折扣系数θ敏感的。在参考了文献[18]的基础上,预付定金的顾客数量与折扣系数和预付定金额成反比,产品销售数量与折扣系数成反比。则假设η=A1-λ1θ-λ2r,r=k0(1-θ),其中A1为常量,λ1>0,λ2>0,k0≥0且1>A1-λ1θ-λ2r>0,1>k0(1-θ)>0。假设a=A2+k1(1-θ),b=A2+k2(1-θ),其中A2为常量,k1>k2>0且1>A2+k1(1-θ)>A2+k2(1-θ)>0(即a>b,A类顾客在折扣θ下最终购买产品的比例比B类顾客大,并且随着价格折扣优惠越大,η值越大,则B类顾客的数量越少,则会导致B类顾客中最终选择购买产品的比例增加)[23]。其中,η、r、a、b均在[0,1]范围内。则此时生产商产品利润Π(p,θ)表达形式如(15)式所示: Π(p,θ)=(θp)×(A2+k1(1-θ))(A1-λ1θ-λ2r)D(p)+ [k0(1-θ)p×[1-(A2+k1(1-θ))]ηD(p)+s×[1-(A2+k1(1-θ))] (A1-λ1θ-λ2r)D(p)]+p×(A2+k2(1-θ)) [1-(A1-λ1θ-λ2r)]D(p)+s×[1-(A2+k2(1-θ))] [1-(A1-λ1θ-λ2r)]D(p)-wD(p) (15) 定理4生产商总利润最大值Π(p,θ)存在近似最优解(p*,θ*)。 [s(k1-k2)+pk1(θ-r)+p(k0(1-a)-b)]} (16) 令x1=p,x2=θ,对(15)式关于(p,θ)及其约束条件转化如下: (17) 显然(17)式中有8个不等式约束,令gj(x1,x2)(j=1,2,…,J,J=8)为(17)式从左往右的第j个不等式约束条件,f(x1,x2)及gj(x1,x2)表示对应函数的梯度,λ=(λ1,λ2,…,λJ)。对于(17)式,由于f(x1,x2)二阶连续可微,若为局部最优解,则存在拉格朗日乘子满足以下条件(或称为KKT条件): (18) 以该KKT条件为理论基础,采用拉格朗日乘子罚函数法对(17)式求近似局部最优解,该方法如下:设δ为大于零的罚参数,令 φ(x1,x2,λ,δ) (19) (20) 通过比较上述算法得到的局部最优解与边界点处的函数值可得到(15)式全局最优解。由上述推导过程,可得存在生产商利润Π(p,θ)最大值的近似最优解(p*,θ*)。关于上述算法收敛性说明,在文献[24,25]的研究中有关于此算法及其改进算法的介绍及收敛性分析,此处不再赘述。 定理4表明若预付定金产品的数量、预付定金比例系数、退货数量是关于价格折扣敏感的,存在近似最优的产品定价和价格折扣组合策略(p*,θ*)。此协调策略(p*,θ*)可以很好的满足不同类型顾客的需求,还能使得生产商获得更好的效益,有效的实现供需双方共赢的局面。 假设二级供应链中相关参数满足以下条件,其中w=3,s=1,a=0.70,b=0.60,θ=0.95,r=0.50,ε=4,K=100000,η=0.50。运用Maple 14.0软件,将各参数代入生产商的确定性模型(1)式和(2)式中,结果如图1所示。 图1 确定性下的生产商销售利润-产品定价分布图 图2 市场需求随机下的生产商销售利润-产品定价分布图 图3 相关参数敏感性分析 为了进一步分析各参数与产品定价、生产商利润之间的关系,采用控制变量,分别对价格折扣系数、预付定金数量比例、A类和B类顾客最终购买比例进行敏感性分析(其中假设a∈[0.6,1],b∈[0.4,0.6]),结果如图3所示。并通过计算,得出不同参数变化情况的生产商利润最大条件下的近似最优决策条件如表1所示。从图3和表1结果可得以下结论:①在保持产品定价和其他条件不变的情况下(图3中各图的横坐标),产品价格折扣系数θ、预付定金数量比例η、A/B类顾客最终购买比例(a和b)均与产品销售利润呈正相关;②在保持产品价格折扣系数、预付定金数量比例、A/B类顾客最终购买比例不变的条件下(图3中各图纵坐标),产品销售利润是随着产品定价的提高而呈现先增加后减少的趋势;③从图3中结果可以得出,θ和η、a和b对产品销售利润影响程度从大到小排列是η>θ,a>b。 表1 不同假设条件下的决策条件 图4 销售利润与产品定价、产品折扣的关系 图5r=0时,利润与定价、折扣的关系 对于相关参数的敏感性分析中,可以看出最优决策条件值均为参数临界值。但是在实际情况中,某些参数会受其他参数的影响和限制。则对于顾客预付定金和退货的优化策略问题,其中η、r、a、b均是关于产品价格折扣敏感的。假设相关参数具体数值为w=3,s=1,ε=4,K=100000,A1=15,A2=0.4,λ1=15,λ2=2,k0=5,k1=3,k2=2。将上述参数数值代入(15)式中,结合定理4中拉格朗日乘子法,运用软件Maple 14.0,得到仿真结果如图4所示。从图4的仿真结果可知:①在保持产品定价和其他条件不变的情况下,随着产品折扣系数η的不断降低,产品的销售利润呈现先增长后降低的趋势;②在保持产品折扣系数和其他条件不变的情况下,随着产品定价p的提高,产品的销售利润也呈现先增长后降低的趋势。③在各参数取值范围内,存在近似最优的(p*,θ*)使得生产商利润获得最大值。以上结论均与定理4中证明结果相符。 根据定理4,在约束条件下,通过求解方程组得到近似最优解(p*,θ*)满足生产商销售利润最大。求得方程组的解为(p=4.68,θ=0.84),生产商利润maxΠ(p)=198.70。进一步获得其他相关参数的具体数值为a=0.88,b=0.72,r=0.81,η=0.81。 假若对于A类顾客退货也返还其预付定金(即r=0),相关参数也用上述数值,通过Maple软件处理得到结果如图5所示。从图5中的仿真结果分析可得其产品近似最优定价和折扣系数p*=5.00,θ*=0.80,最大利润maxΠ(p)=159.94。由于从相关参数数值假设,推导得出θ∈[0.80,1],由此可知θ*=0.80是θ∈[0.80,1]中的最小值。即说明假若顾客退货需全额退款的条件下,生产商需尽量的给与顾客较大的产品价格折扣,来降低由顾客退货所导致的销售损失,进而获得较高的产品销售利润。但是,过低的产品价格折扣,也会给生产商带来损失。如假设参数中k1=1,k2=0.5,η=0.5,其他参数不变,运用Maple软件得到仿真结果,如图6所示。得到此时的产品最优定价和最优产品折扣系数p*=6.68,θ*=0.56,最大利润maxΠ(p)=45.71。此时,在产品定价p=6.68保持不变的情况下,若θ<0.56,则生产商的销售利润会降低。 假设a,b与θ无关,令a=1,b=0.8,其他参数不变。代入相关参数数值,可得仿真图7。从仿真结果分析可得其产品最优定价和最优折扣系数p*=4.53,θ*=0.92,生产商获得最大利润maxΠ(p)=227.96,另计算得r=0.39,η=0.39。从图7仿真结果可得,在保持产品定价不变的情况下,随着产品折扣系数数值不断降低,产品的销售利润是出现先增长后降低的趋势;在保持产品折扣系数不变的情况下,随着产品定价p的不断提高,产品的销售利润也出现先增长后降低的趋势。 图6r=0,k1,k2,η为定值时,利润与定价、折扣的关系 图7a,b与θ无关时,利润与定价、折扣的关系 随着互联网经济的蓬勃发展,“互联网+”相关问题成为近些年被关注的研究热点。其中,“互联网+制造业”将成为未来工业发展新红利的主要途径,并逐渐出现很多新的产品销售模式来推动制造业的发展。本文针对生产商网上直销模式中,产品销售存在顾客预付订单和顾客退货的背景条件下,研究生产商的产品定价及优化问题。构建了存在预付定金和退货的销售模式下市场需求确定和随机的利润最大化模型,利用极大值原理和两阶段优化法,分别得出了生产商产品网上直销最优定价的解析解;并同原不考虑预付定金的销售模式进行比较,得出相关参数在满足定理2的条件下,采用预付定金的销售模式会获得更好的收益;通过数值算例验证了产品定价和销售利润之间的存在着先增长后降低的趋势,通过对比可得出市场需求随机情况下的销售利润小于确定型市场需求类型的销售利润;并对模型中的价格折扣系数、预付定金数量比例、A类和B类顾客最终购买比例进行敏感性分析,得出各类情况下商品网上直销的销售利润与各变量指标之间的关系,即变量指标在最大值情况下,生产商直销的销售利润最大。然后,进一步对预付定金产品的数量、预付定金比例系数、退货数量关于价格折扣敏感的决策问题进行研究,构建该类情况下生产商直销销售利润最大化模型,运用拉格朗日乘子法构建相应算法,并通过实例验证了其存在利润最大化情况下的近似最优的产品定价和价格折扣组合策略,并得出此时最优的预付定金的产品数量、预付定金比例系数和产品退货数量。最后,讨论了A类/B类顾客退货均全额退款(r=0)情况下的产品销售利润与产品定价、价格折扣之间的关系,进过分析得出其也存在最优的定价和价格折扣方案;同时,也对A类/B类顾客其退货量为定值的这一特殊情况进行分析,得出该种情况下亦存在其产品最优定价和最优折扣。 根据本文研究结果可以得出,线上直销的生产商需根据不同的市场需求和类型,及时适当的调整销售模式和销售策略,进而获得更大的销售收益。其中,较为有效的措施之一是保证产品的质量,尽量降低商品在配送途中的损耗,进而有效的降低顾客的退货率,从而保证产品销售利润;另一主要途径为适当的给与预付定金的顾客相应的价格折扣优惠,刺激顾客的购买行为,进而降低市场需求不稳定带来的风险,保证生产商获得较高收益。另外,本文还有一些方面可以进一步拓展和研究。首先,模型可以扩展为多周期产品销售问题,其中退货的产品可以考虑进行二次销售。其次,模型可以拓展为多产品销售模式,或者是多代产品销售的模式(可以“以旧换新”)。最后,关于顾客的购买行为、退货行为的行为研究,也可以是以后进一步深入的方向。2 模型构建
2.1 确定性问题
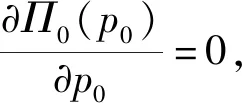

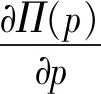

2.2 两种不同的销售方式比较
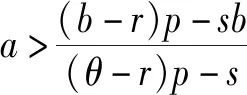
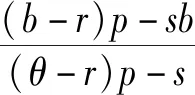
2.3 随机性问题
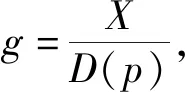













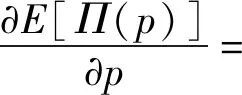

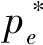
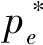

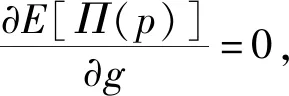

3 顾客预付定金和退货的优化策略研究

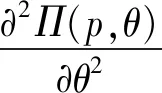
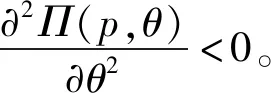
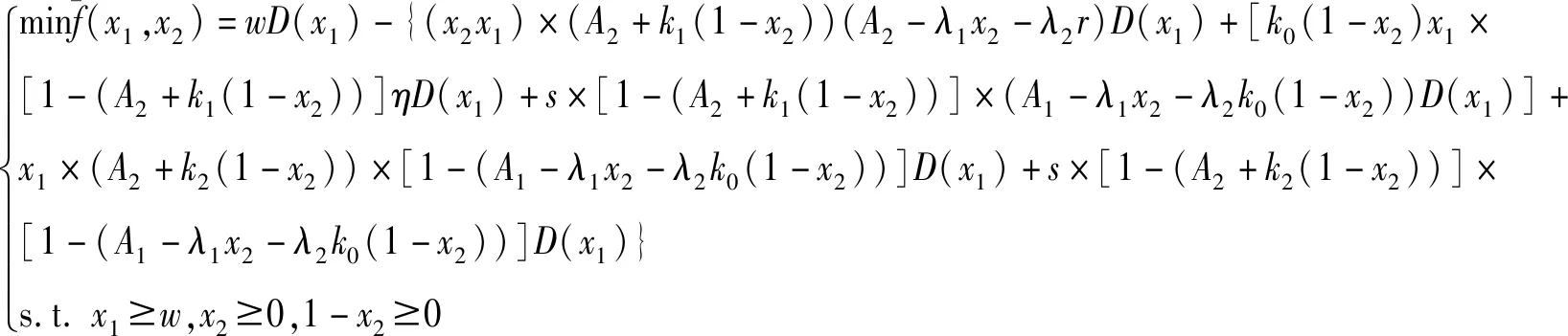

4 数值算例








5 结论
