我国大类资产信息溢出机制研究——基于方差分解的网络拓扑分析

周 亮

(1.湖南财政经济学院 学报编辑部，湖南 长沙 410205; 2.湖南师范大学 商学院，湖南 长沙 410081)

0 引言

随着经济一体化程度越来越高、投资者越来越成熟，大类资产市场之间不再是分割的个体，而是联系越来越紧密，相互之间的影响越来越密切，风险的传染也越来越迅速。国际上关于金融市场互动关系的研究文献，多数是以欧美主要股市为研究对象(Koutmos and Booth[1]；Fratzscher[2]；Bodart and Candelon[3])，后来扩展到对于汇市之间、债券市场间联动关系的研究(Hong[4]；Inagaki[5])，研究结论表明国际主要股市间存在明显的溢出效应，可以称之为金融传染(Forbes and Rigobon[6])。国内学者方面，大部分研究同样集中在对股市信息溢出的研究(冯旭南和徐宗宇[7])以及沪深股市与香港或美国股市之间的信息溢出机制(李红权、洪永淼和汪寿阳[8]；刘磊和王宇[9])，还有学者研究了股市内部行业间的信息溢出情况(黄玮强、庄新田和姚爽)[10]，也有学者对股市与债市之间的信息溢出(徐信喆、杨朝军和陈强)[11]、国际石油价格对股市的信息溢出(宋科艳)[12]、人民币汇率市场对股市的信息溢出(陈云)[13]进行了研究。还有一些文献研究了其他市场间的信息溢出情况，如刘向丽等[14]分析了商品期、现货两个市场间的信息溢出效应；陆凤彬和洪永淼[15]研究了上海期货交易所(SHFE)和伦敦金属交易所(LME)铜期货市场间信息溢出的时变特征；罗荣华和门明[16]建立基于t分布的VECM-MVGARCH-BEKK模型研究了股指期货和现货市场的信息溢出效应；邓宏亮和黄太洋[17]采用线性及非线性Granger因果检验方法研究了我国粮食期货市场价格与汇率之间不同阶段的信息传递溢出；黄文彬和李海栗[18]分析了全球主要碳金融工具的信息溢出效应；张海亮和饶永恒[19]运用信息溢出检验方法(Hong方法)详细分析了我国稀有金属现货市场内各品种间的信息溢出效应及国内外稀有金属现货市场间的信息溢出效应。

常见的用于检验信息溢出的方法有线性或非线性Granger因果检验、多元GARCH模型、CoVaR等。而Diebold和Yilmaz[20]基于向量自回归模型中传统正交方差分解方法提出的总体溢出指数，能够更直观地描述多个市场间的总体溢出方向和大小。但该方法同样存在缺陷，其所依赖的Cholesky分解方法的结果会受到变量次序的影响。因此Diebold和Yilmaz[21]对该方法进行改进，在广义预测误差方差分解的基础上构建更具有普遍性的溢出指数，消除了由于变量排序不同造成的结果差异问题。Barunik et al.[22]对Diebold和Yilmaz的模型进行了改进，采用高频数据区分出正向波动和负向波动，从而考察了美国股市上波动溢出的非对称性。随后该方法被引入国内，大量学者采用该方法对不同金融市场之间的信息溢出进行了研究。梁琪、李政和郝项超[23]采用溢出指数方法研究了全球17个国家或地区的股票市场的联动，测度了中国股市信息溢出的方向、水平和动态趋势；李政、梁琪和涂晓枫[24]构建了我国上市金融机构之间的关联网络，通过网络分析法解构了金融网络的总体关联性以及部门内和部门间的关联特征；欧阳红兵和汪清梅[25]基于方差分解的网络拓扑结构对我国13家主要上市银行机构的股票波动率的关联度进行了度量及分析；尹力博和吴优[27]采用广义溢出指数法研究了离岸人民币与中国周边国家(地区)货币的溢出效应及其时变特征；徐晓光、廖文欣和郑尊信[27]运用广义溢出指数法对比分析了沪港通开通前后中国内地与中国香港股市行业间波动溢出效应的变化及其形成机理。

但是较少有学者将股票市场、期货市场及债券市场综合一起考虑，用广义溢出指数法分析三个市场之间信息溢出的更为少见。考虑到采用经济周期或货币周期划分的投资时钟，可以有效的在大类资产之间进行轮动配置，从而获得较为稳定的超额投资收益(周亮[28]；郜哲[29])，因此从信息溢出角度研究三个市场之间的内在传导机制，具有较强的理论和现实意义。并且，目前国内对Diebold和Yilmaz方法进行研究的文献，还很少有涉及到对正负波动溢出非对称性的研究。因此，本文将借鉴Diebold和Yilmaz[21]提出的广义溢出指数研究方法，通过基于方差分解的关联性表及拓扑网络来分析我国股票、期货和债券三个市场间的收益率溢出和波动率溢出情况，并且通过将波动分为正向波动和负向波动，考察了波动溢出的非对称性；同时考虑到2015年6月我国发生了举世瞩目的股灾，不仅导致股市千股一再跌停，同时风险也向其他资产市场扩散，因此讨论了股灾发生前后6个月时间里三个市场的波动率溢出的变动情况，除了可以更好的利用广义溢出指数分析三个市场的溢出机制外，也能为投资理论和实践提供更充分的指导依据。

1 研究设计

1.1 大类资产关联网络的构建及特征刻画

网状拓扑结构主要指各节点通过传输线互相连接起来，并且每一个节点至少与其他两个节点相连，主要应用在计算机领域，用网络拓扑结构来描述大类资产之间的关联网络，可以很好的描述出大类资产之间的信息溢出机制。采用向量自回归(VAR)模型来研究大类资产之间的关联关系，向量自回归模型是基于数据的统计特征，将系统中每一个内生变量作为系统中每一个内生变量的滞后值的函数来构造的模型，常用来预测相互联系的时间序列系统及分析随机扰动对变量系统的动态冲击。方差分解给出的则是VAR模型中的变量产生影响的每个随机扰动的相对重要性的信息，可以用方差分解将网络拓扑分析中复杂的系数矩阵转化为可反映系统关联性的矩阵——关联性表。根据Diebold and Yilmaz[21]的方法，选择冲击期为12期的方差分解可以测算出大类资产之间的关联性表。略有不同的是，本文选取的是2010年1月至2017年12月的所有周数据进行测算，考虑到一年的交易周约为50周，因此形成期采用50期，而不是像Diebold and Yilmaz[21]采用的100期。具体的关联性表构造如表1所示：

表1 拓扑网络的关联性表

1.2 样本选择及描述性分析

表2 三类资产收益率及波动率的描述性统计情况

表3报告了三类资产在整体样本区间的收益率和波动率之间的相关系数。可以看到，收益率方面，股票和期货在1%的显著性水平下存在着正相关关系，期货与债券在5%的显著性水平下存在着负相关关系，但是股票和债券之间却没有显著的相关性；波动率方面，股票与债券在1%的显著性水平下存在着正相关关系，期货与债券之间也存在着显著的正相关关系，但是股票和期货之间的相关性却不显著。因此，综合来看，三类资产之间的收益率或波动率之间存在着一定的相关关系。但是表3只是整体样本区间的静态分析，且只能简单看出资产之间的两两相关性，无法判别相互之间的影响机制，因此下文将采用基于方差分解的网络拓扑分析来研究资产之间的信息溢出机制。

表3 三类资产之间的收益率及波动率间的相关系数表

注：*、**、***分别表示在10%、5%、1%水平下显著。

2 实证检验与结果分析

2.1 全样本信息溢出分析

采用表1的方法研究样本区间内三类资产之间的信息溢出机制，表4报告了相关研究结果。可以看到，无论是收益率还是波动率，三类资产均主要是受到自身的影响(从对角线上的数值大小看出)，综合来看，股票对自身的影响最大，债券对自身的影响最小。收益率溢出方面，股票对其他资产的溢出值为28.6，而受到其他两类资产的溢出影响为14.13，因此股票的净溢出为14.47；期货对其他两类资产的溢出影响为23.67，但是受到其他两类资产的溢出影响为25.96，净溢出为-2.29；债券对其他两类资产的溢出影响为16.48，受到其他两类资产的溢出影响为28.67，净溢出为-12.19；综合来看，股票对其他两类资产有收益率溢出影响，而期货和债券则处于收益率的被溢出影响状态。波动率溢出方面，股票的净溢出为9.82，期货的净溢出为8.74，债券的净溢出为-18.56，因此与收益率溢出有所不同，股票仍然对其他资产有波动率溢出影响，但是期货也是处于波动率溢出状态，只有债券处于被溢出状态。因此，整体来看，股票对期货和债券均有收益率溢出影响，而股票和期货对债券均有波动率溢出影响。从整体溢出指数来看，收益率溢出的综合值为22.92，波动率溢出的综合值为20.82，相对于100的总体分值，综合值均偏低，表明我国不同资本市场之间的相互影响相对来说并不是很大。

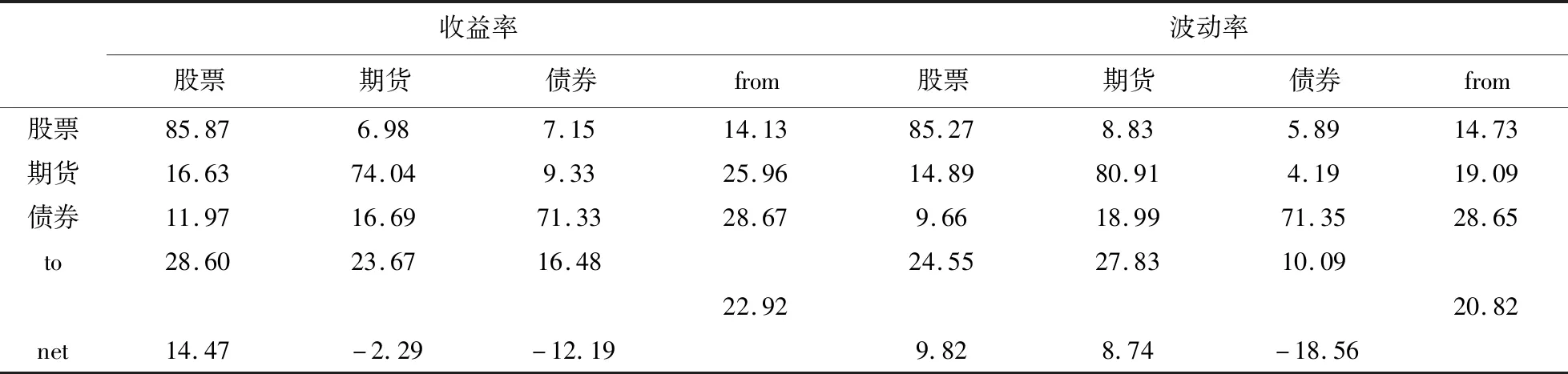
表4 全样本信息溢出情况表

通过大类资产两两之间的溢出值大小，可以更清晰的看到资产之间的溢出情况，图1报告了收益率溢出和波动率溢出的拓扑网络图。可以看到，在收益率溢出方面，股票对期货有9.65的净溢出，而对债券有4.82的净溢出，期货则对债券有7.37的净溢出；波动率溢出的方向与收益率溢出相同，只是数值上有所差异，股票对期货的净溢出为6.06、对债券的净溢出为3.76，而期货对债券的净溢出为14.79。因此可以看到，股票在三类资产中处于净溢出状态，而期货则受到股票的溢出、以及对债券进行溢出，相对来说，股票对期货市场的溢出比对债券市场的溢出更大，而期货对债券市场的溢出比股票对债券市场的溢出更大，说明股票与期货市场之间、期货与债券市场之间的联系相对更为紧密。

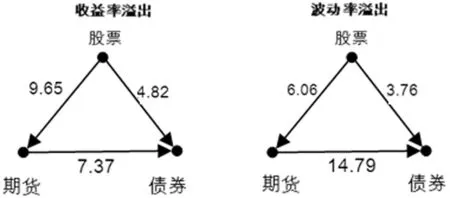
图1 资产之间净溢出拓扑网络图

2.2 信息溢出的时变特征分析

2.2.1 整体溢出时变特征

三个市场的整体溢出情况如图2所示，可以看到，对于收益率整体溢出而言，2015年之前总体处于下降趋势，但是在2015年之后逐渐上升；溢出值最大的是2012年的33.36，说明各资产之间的影响占到了整体影响的三分之一(33.36/100)左右，总体溢出较高，溢出值最小的是2015年的15.70，各资产之间的相互影响只占到整体影响的七分之一(15.70/100)左右，相对于2012年有了明显下降，2017年整体收益率溢出又上升到了23.26，各资产之间的收益率溢出有进一步上升的趋势。对于波动率整体溢出而言，2015年之前总体处于下降趋势，这与收益率溢出相似，但是2016年波动率溢出虽然上升了，2017年却下降了；波动率溢出的最大值出现在2011年的28.55，最小值出现在2015年的14.48。相对于收益率溢出而言，波动率溢出整体趋势大体相似，但是数值略小。

图2 大类资产整体溢出情况

2.2.2 各资产净溢出时变特征

图3报告了三类资产净溢出的时序变动特征。可以看到，不同于整体溢出，各资产的收益率净溢出与波动率净溢出并不同步。股票的净溢出方面，除了2011年波动率净溢出为负之外，其他所有年份的收益率净溢出和波动率净溢出都为正，说明股票资产整体处于对其他资产有溢出影响的状态；收益率净溢出的最高值出现在2017年的31.01，最小值出现在2016年的0.88；波动率净溢出的最高值出现在2014年的36.61，最小值出现在2011年的-7.69；总体而言，股票处于净溢出状态，且部分年份对其他资产的溢出影响效应很强。期货的净溢出方向则并不稳定，无论是收益率溢出还是波动率溢出，均是有正有负，说明期货资产部分年份对其他两类资产有净溢出影响，部分年份则是受其他两类资产的净溢出影响。债券资产除了收益率溢出在2016年为正，其他年份的收益率溢出和波动率溢出均为负，且收益率溢出的最小值出现在2017年的-28.63，波动率溢出的最小值出现在2016年的-35.42，说明债券资产处于受其他两类资产溢出影响的状态，而且被溢出的程度还较高。

图3 各类资产的净溢出情况

2.2.3 资产间信息溢出时变特征

图4报告了三类资产两两之间的信息溢出时变特征情况。可以看到，股票对期货的信息溢出在大部分年份均为正，除了2014年的收益率溢出及2011年的波动率溢出，且收益率溢出的最大值为2012年的25.59，波动率溢出的最大值为2014年的21.38，说明股票对期货的信息溢出较大。股票对债券的信息溢出在大部分年份均为正，除了2016年的收益率溢出及2012、2013年的波动率溢出，且收益率溢出的最大值为2017年的17.36，波动率溢出的最大值为2014年的15.24，相对于股票对期货的信息溢出值而言，股票对债券的信息溢出相对较弱。期货对债券的信息溢出大部分年份为正，除了2014年的收益率溢出和2017年的波动率溢出，且收益率溢出的最大值为2011年的26.65，波动率溢出的最大值为2012年的34.89，均要大于股票对期货的信息溢出，说明期货对债券的信息溢出是所有资产间溢出最大的。

图4 资产间的信息溢出

2.3 基于GARCH波动率和已实现波动率(RV)的稳健性检验

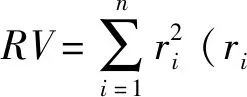
表5 GARCH波动率和RV波动率的信息溢出情况表

图5 资产之间GARCH波动率和RV波动率溢出拓扑网络图

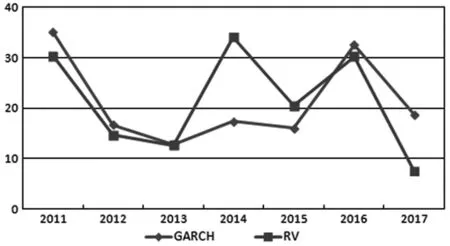
图6 GARCH波动率和RV波动率溢出时变特征

2.4 波动率溢出的非对称性检验

考虑到波动率溢出可能存在着非对称性(Barunik et al.[22])，即正向波动溢出跟负向波动溢出可能存在着差异，因此通过采用高频数据来区分正向波动和负向波动，从而考察大类资产间波动溢出的非对称性。正向波动的计算公式为

负向波动的计算公式为

分别计算出股票、期货和债券三个序列的正负向波动序列，并采用Diebold and Yilmaz方法分别计算出正负波动溢出情况，结果如表6和图7所示。从表6可以看到，整体来看，正向波动溢出要比负向波动溢出高：正向波动总溢出值为21.92，高于负向波动总溢出值的18.78；股票、期货和债券正向波动净溢出分别为31.54、19.15和15.08，均要高于负向波动净溢出的25.45、18.21和12.67；股票、期货和债券正向波动接受溢出值分别为16.40、24.44和24.93，均要高于负向波动接受溢出值的14.64、19.27和22.43。从图7正负向波动总溢出值的走势图来看，除2012年外，正向波动溢出均高于负向波动溢出，但是经检验，两个序列配对检验T值为1.11，在5%水平上并不显著。因此综合来看，大类资产间正向波动的溢出要略高于负向波动的溢出。这与Barunik et al.等学者的研究结论有差异，大多数学者研究均指出负向波动的溢出会高于正向波动，这是由于羊群效应更容易导致危机扩散。但是考虑到本文研究的是国内的大类资产市场，受到共同的货币环境、经济政策等影响，在货币宽松时期，更容易出现共同上涨现象；但是由于国内金融工具不如发达市场多元，在某个市场发生危机时，为了资产分散化需要，在其他市场的资产配置可能受到的影响更小，从而才导致了负向波动溢出值更小。

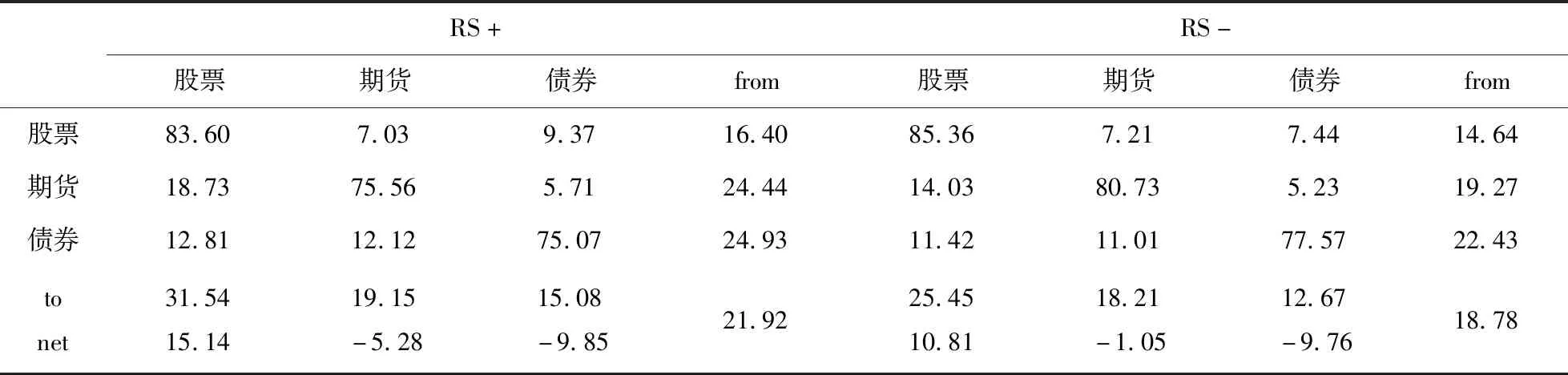
表6 正负向波动的信息溢出情况表

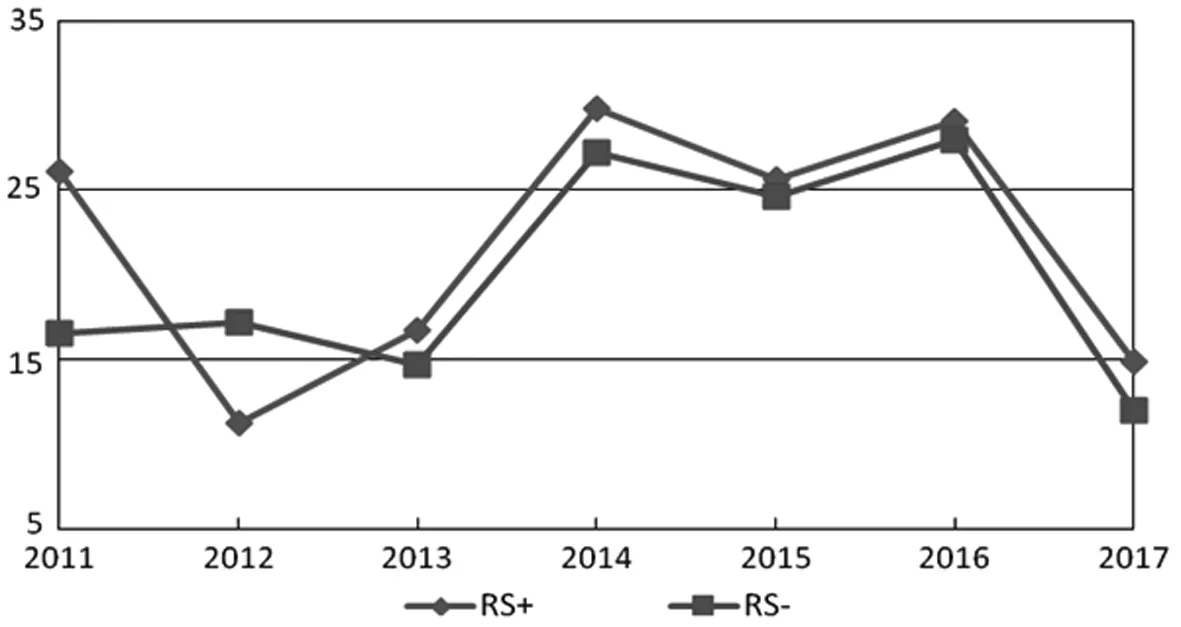
图7 正负向波动溢出时变特征

2.5 进一步讨论：股灾对资产间信息溢出的影响

2015年6月我国股市发生了举世瞩目的股灾，不仅传染到了国际股市，而且对我国期货和债券市场也产生了一定影响。通过信息溢出机制可以较好的反映出股灾前后我国大类资产之间的风险传染情况，选取股灾前后一共6个月的时间，采用50周的滚动时间窗口计算这6个月内每周的波动溢出状况，如2015年6月19日当周的波动溢出采用2014年7月4日至2015年6月19日的数据计算，依次类推。图8报告了三类资产在股灾前后的波动率净溢出情况。可以看到，股票市场一直处于波动净溢出状态，但是在股灾发生前净溢出逐渐降低，但是在7月10日当周突然增大。这里需要说明的是，股票市场净溢出突然增大之所以不是股灾发生的6月末，主要原因有两点：一是广义方差分解法采用的是50周的滚动时间窗口数据，虽然近期的数据影响更大，但是也会受到远期数据的影响，因此会导致结果存在一定的时滞；二是股灾虽然发生在6月末，但是恐慌情绪往其他市场传染存在时滞，如期货市场在6月份并没有出现下跌，在7月10日当周却出现了4%以上的下挫。因此可以看出，股票市场的风险在发生股灾之后向期货市场进行了扩散，而从图8可以看到，债券市场在股灾期间的风险溢出并没有扩大，反而从股灾前的被溢出状态转变为微弱的净溢出状态。图9对资产间两两之间的溢出关系进行了详细说明，可以更清晰的看到，股灾期间股票市场对期货市场产生了极大的风险溢出，且在股灾之后的溢出水平比股灾之前均有所提高；但是债券市场的被溢出状态却一直处于下降，股灾之后甚至对股票市场从被溢出变成了净溢出。因此，综合来看，在股灾等极端风险发生时，股市的风险更容易向期货市场传染，而债券市场却相对更为稳定，不容易被极端风险感染。这是由于我国资本市场上股市和期货市场的投机氛围更重，股市和期货市场上散户投资者参与甚众，当一个市场因极端事件发生暴跌时，另一个市场也容易因羊群效应而出现踩踏；而债券市场主要是银行间市场，外部监管和内部风控更严格，且我国债市由于政府隐性担保，因此总体波动极小，相对来说也更为稳定。

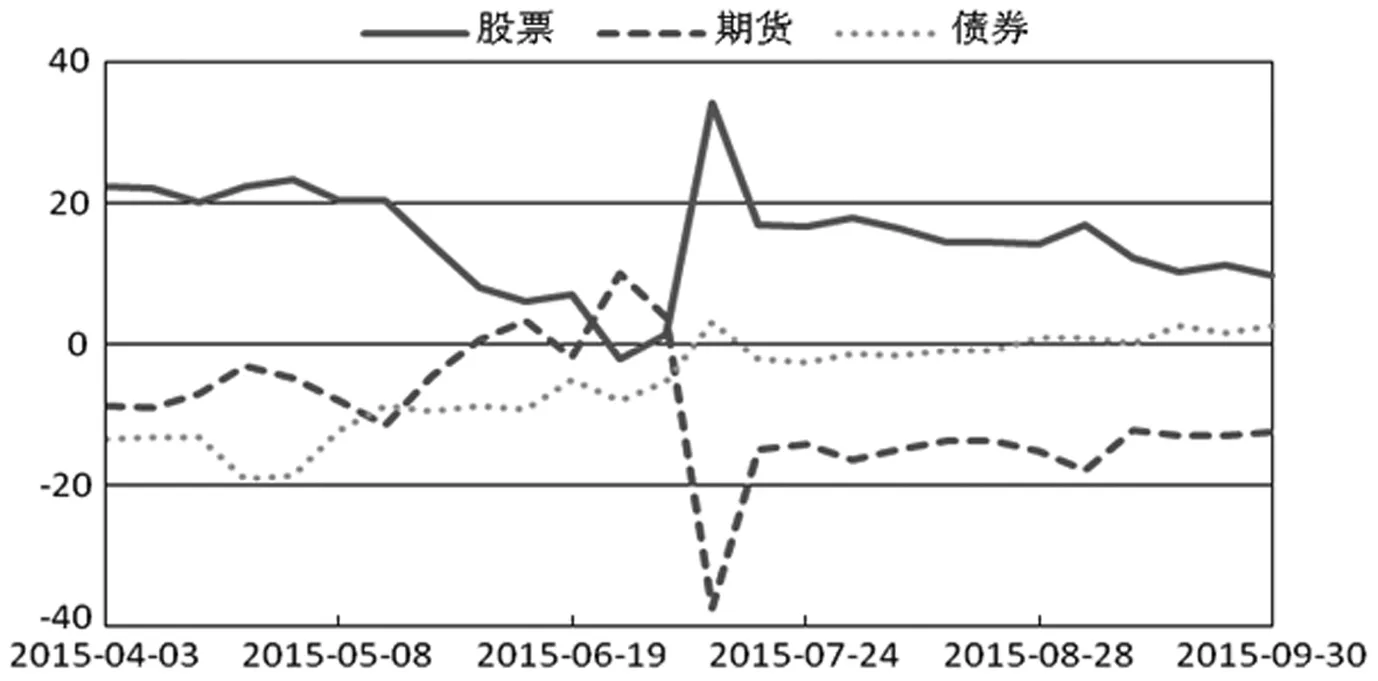
图8 三类资产在2015年股灾前后的波动率净溢出时变特征图

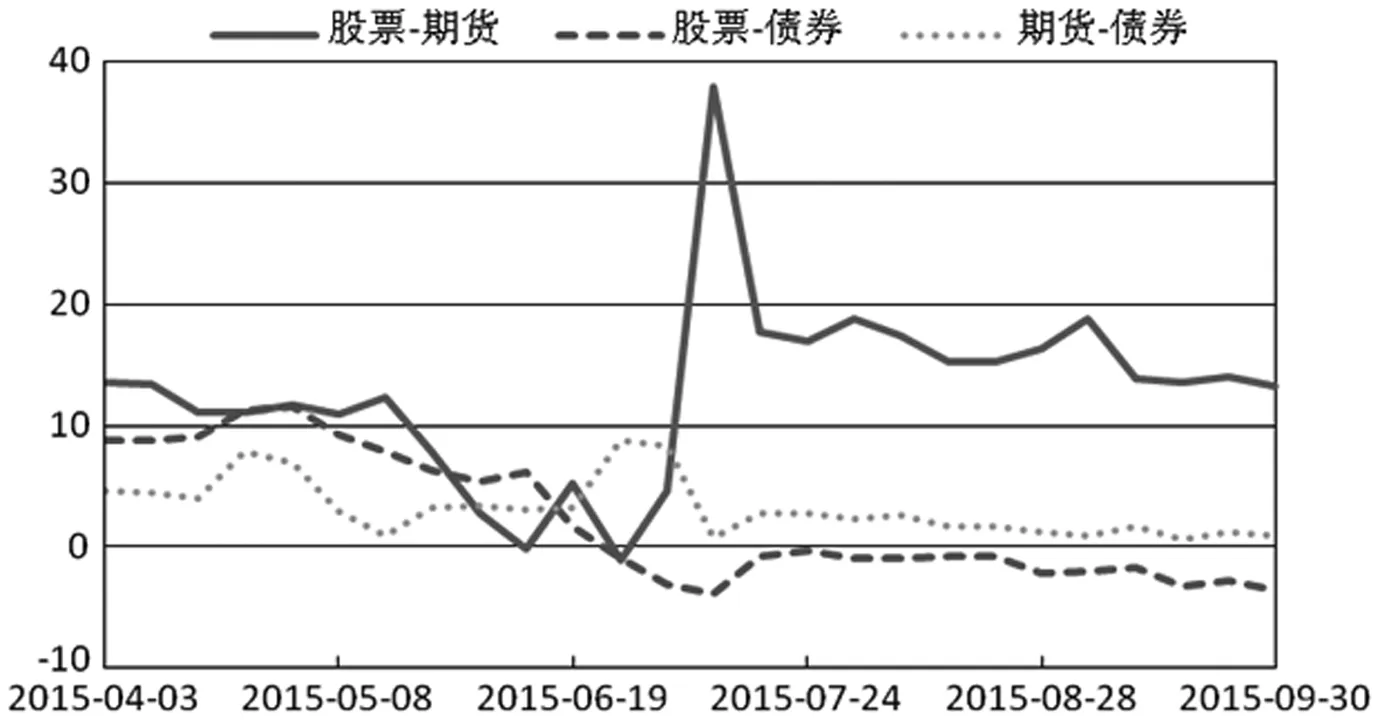
图9 股灾前后资产间的波动率溢出时变特征图

3 研究结论与政策建议

根据Diebold和Yilmaz[21]提出的广义溢出指数研究方法，对2011年至2017年我国股票市场、期货市场及债券市场的周收益率和周波动率数据进行分析，以探讨三个市场之间的信息溢出机制，结果发现：收益率溢出方面，股票对其他两类资产有溢出影响，而期货和债券则处于被溢出的状态；波动率溢出方面，股票和期货均处于溢出状态，只有债券的处于被溢出状态；从整体溢出指数来看，收益率溢出的综合值为22.92，波动率溢出的综合值为20.82，相对于100的总体分值，综合值均偏低，表明我国不同资本市场之间的相互影响相对来说较小；从时变特征上也能看出相同的状况，股票在所有年份里的收益率净溢出和波动率净溢出大多为正，期货则时正时负，债券则大多为负，表明股票大多数情况处于溢出状态，期货方向并不明确，而债券则大多数情况处于被溢出状态；通过对正负向波动溢出情况进行对比分析波动溢出的非对称性，结果发现正向波动溢出整体来看要高于负向波动的溢出，但是在统计上并不显著。对2015年6月股灾前后三个市场的波动率溢出分析后可以发现，在股灾等极端风险发生时，股市的风险更容易向期货市场传染，而债券市场相对更为稳定，不容易被极端风险感染。本文的研究很好的将其他学者对资本市场信息溢出的结论和方法扩展到了更大范围的大类资产，同时对波动溢出的非对称性进行了探讨，这也是本文的创新之处。

本文的研究具有一定的理论和现实意义，对于投资者和监管层也提供了很好的政策依据：第一，我国股票市场和期货市场的联动更为紧密，而且更多的是股票市场对期货市场的传染，因此对于期货市场投资者而言，除了加强对期货市场本身的研究之外，需要对股市也保持足够的关注，对于监管层而言，则应该在股市发生风险时，即时出台政策，防止期货市场也出现过度的反应；第二，债券市场虽然整体而言处于被溢出状态，相对于股票和期货市场，更容易受到其他市场的影响，但是通过对股灾期间波动率溢出的分析，可以看到，在其他市场极端风险发生时，债券市场反而会从被溢出状态转变为溢出状态，因此应该加大债券市场建设的力度，同时加强投资者教育，吸引更多的投资者进行债券市场的投资，而不是只关注更高风险的股票和期货市场；第三，本文的研究验证了各资产市场之间的联动性，因此通过识别周期拐点进行大类资产配置是合适的，正像很多学者所证明的，投资的绝大部分收益来自于资产配置，而不是择时或选股，因此对于机构投资者而言，应该大力加强资产轮动配置的研究，在降低投资风险的同时也能够有效扩大投资收益。