具有质量差异的项目支付进度问题研究——以软件项目为例

曹 萍， 张 剑， 熊 焰

(1.上海应用技术大学 经济与管理学院,上海 201418; 2.上海工程技术大学 航空运输学院,上海 201620)

0 引言

项目支付进度问题(Project Payment Scheduling Problems, PPSP)是现金流管理的一个重要内容，以资金的净现值最大化为目标，研究如何合理的安排支付的时间和次数等，是项目管理的热点研究领域[1]。由于项目的支付进度会对双方的收益产生重要影响，因此是承包商和客户共同关注的问题[2]。Russell首次将净现金流量(Net Present Value，NPV)引入项目进度领域，将项目支付进度问题描述为基于活动弧(Activity on Arc，AOA)的非线性规划问题；Naber等研究了不同资源分配模式下的项目进度支付问题[3]；Dayanand和Padman分别从承包商和客户角度，以NPV为目标构建了各自的优化模型，设计了基于AOA两阶段搜索的启发式算法和混合整数规划算法分别对模型进行了求解[4,5]；Ulusoy和Cebelli则从双方联合的角度研究了项目支付进度问题[6]，提出用double-loop遗传算法对模型进行求解；Antonio等研究了资源约束和多种执行模式的项目支付进度问题，并设计了MM-HGA算法对模型进行了求解[7]；Wolfram和Daniel研究了不确定环境下的项目支付进度问题[8]。这些研究均未考虑奖惩机制的影响。

在项目实践中，为了使项目在规定的时间内尽快完工，客户通常以项目到期时间为基准设置奖惩机制以防止承包商拖延时间,从而提高项目的收益[9]，而承包商则在客户给定的奖惩强度下安排项目进度。具有奖惩结构的项目进度问题一度成为研究者们关注的热点，并出现了许多研究成果。如Jin等针对工期设计了激励合同，用于对工期的激励[10]；Abdulaziz等设计了对成本进行激励的激励合同[11]；He和Xu研究了在项目截止日期设置奖惩机制的多模式项目进度支付问题[12]；Moslem以时间作为激励因子，构建了含有时间奖惩结构的项目支付进度模型[13]，并设计了求解模型的遗传算法。Hosseinian等将成本与工期同时作为激励因子构建了承包商效益优化模型[14]；等。可见，现有关于奖惩因素的基本上与时间和成本有关，缺乏针对其它激励因素的研究。但项目管理中并非只有这两个目标，Berends就认为环境保护、质量等也是重要的激励因素[15]。陈勇强等认为工程项目中质量目标随着时间推移而逐渐增强[16]。因此，以质量为激励因子设置合理的奖惩结构，以及在此条件下如何合理的安排项目支付进度使各方收益最大化，是项目管理领域一个具有重要的理论意义和现实价值的研究问题。

近年来，随着信息技术的快速发展和企业信息化需求的日益增加，软件项目的数量和规模均快速增长。与传统工程项目相比，软件项目通常具有开发时间长、复杂程度和风险程度高等特点，并且客户对质量更为敏感，所以软件项目中常以质量作为衡量项目成败的重要指标。此外，软件项目开发中，客户的需求经常会发生变化，这种变化会干扰接包方的工作，导致延期或增加额外的成本，降低项目质量。因此，软件项目的质量问题更为突出，合同的设计是缓解该问题的有效手段[17]。本文以软件项目为例，研究一定资金约束下具有质量激励因子的项目支付进度问题，分别从客户和承包商的不同视角构建具有奖惩结构的收益优化模型，寻找平衡客户—承包商收益的相对“公平”的支付进度，并考查了风险态度对收益的影响。收益滞后性的影响。针对模型的特点，本文采用混合的启发式算法对模型进行求解。

1 问题的描述及研究的假设条件

软件外包中常见的合同类型有固价合同和时间材料合同。固价合同是承包商按照要求完成项目后，客户以确定的价格进行支付，通常适用于需求变化不大的情况。这种合同缺乏灵活性，需要有明确的质量评价标准和绩效指标依据，对客户较为有利[18]。时间材料合同按照承包商投入的成本进行支付，要求客户全程观测和监控项目过程，掌握承包商的投入和努力程度，适用于客户需求变化大的外包项目。这类合同具有较好的灵活性，对承包商更为有利。Dey等认为软件外包项目的合同可以分为两个阶段：设计阶段和开发阶段[19]，并在两个阶段分别采用固定价格合同和基于绩效的合同，来达到系统的最优收益水平。张宗明等将IT 服务外包合同分为三个阶段：合同签订阶段、实施阶段和支付阶段，认为第一个阶段是最重要的阶段，客户企业根据需求和目标提供合同，承包商根据合同计算期望收益，选择接受或拒绝合同[20]。因此，当客户具有较大的议价权时，客户为减少风险，会倾向于选择固价合同；如果同时客户需求较明确，不会存在大的范围变更，即需求波动不大的情况，此时承包商会接受采用固价合同。

软件外包项目的高风险性导致其结果通常具有不确定性，如不符合要求、超出预算、项目滞后以及接包方的服务不能达到要求等。任龙等根据风险的来源，认为外包项目中最主要的风险是道德风险与逆向选择问题[21]，而承包商努力程度是最常见的道德风险[22]。为减轻这些风险，合同的设计和优化是广泛应用的工具和手段[20]。外包中客户在合同设计上掌握着更大的主动权，为规范承包商行为，通常会在合同中采取激励或惩罚机制。其中合同中付款条款的设计是最为有利的工具，在不违背激励相容的原则下设计合同中的付款条款，从而起到既能有效控制风险又能约束承包商行为的目的[23]。

本文考查固价合同情境下客户为激励承包商交付高质量产品的支付进度问题，具体思路是：将合同总价分为两部分，后一部分为“留置”部分，作为一种“激励”基金，这部分钱款在项目交付时通过对项目质量的评价等级决定其去向。即通过“留置”部分对承包商的行为进行约束。以上分析和已有的研究成果，提出研究的假设条件并对符号进行定义。

1.1 研究假设

1)软件质量与承包商的表现水平正相关[24]；即软件质量等级由承包商的表现水平决定；

2)软件项目合同采用固定总价合同方式，即项目的应付款是固定的；

3)总价、支付的数量、费用结算的比例由双方协商确定；总价由固定款项及“留置”款项两部分构成，即U=UA+UB，UA是固定款项，与软件质量无关，UB的支付数量与交付质量有关。

4)合同款中预留一定比例的资金在项目结束后依据软件质量的等级进行支付，留置款的比例由双方协商确定；

5)软件项目发生的费用按一定比例在其开始和结束节点之间进行分配；承包商的费用在每个活动执行的期间发生，但在活动完成后支付；

6)在项目结束时, 软件项目的质量按照事先约定的标准进行评估。根据评估结果，确定留置款项的分配；

7)客户的收益与软件质量水平有关，客户的现金流在项目结束交付使用后发生；

8)承包商在不同的表现水平下花费的费用和时间不同；

9)客户在里程碑事件发生时对承包商进行支付， 在每一个里程碑事件完成后支付一部分工程款。

1.2 问题描述

假设该软件项目由N个活动和E个事件组成，其中活动集N={1,2，…，n}，事件集E={1,2，…，e}。本文采用基于事件的方法研究该项目, 即将项目用一个具有现金流入和流出的Activity-on-Arc(AoA)网络来描述。该网络图是一个由节点和箭线组成的有向图，图中每一个节点代表一个事件，每一条箭线代表一个活动。K代表支付点集合，K= {1,2，…，k} 。pk表示第k次支付的数量。设该项目的合同总价款为U,项目预期收益为B，表1是文中用到的符号定义。

表1 符号及其定义

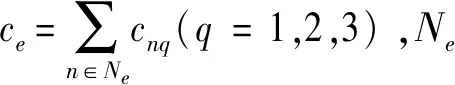
本问题是求解使承包商和客户收益最大的最优支付进度安排，由4个向量组成：最优支付事件集合X*={e:xke=1,k=1,2,…,K}、事件发生时间集合T*={t:yet=1,e=1,2,…,E}、表现水平q和支付量集合P*={pk,k=1,2,…,K}。后两个向量并非独立向量，受到前两个向量的影响。

2 模型构建

根据以上对问题的描述，分两步构建模型。首先构建没有惩罚结构下承包商和客户的净现金流量最大化的模型，在此基础上，构建具有质量惩罚结构的双方现金流最大化模型。

2.1 基本优化模型

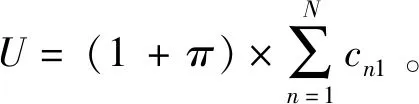
(1)

(10)

目标函数式(1)表示对承包商的收益最大化，本模型中承包商收益用NPV表示；约束表达式(2)是对事件发生时间的约束，即事件e一定在其时间窗[ESe,LSe]内发生；约束式(3)将支付与事件联系起来，即支付在事件处发生；约束式(4)表示在一个事件处安排的支付次数最多为一次；式(5)为活动(v,w)的开始和结束事件的优先关系约束。 式(6)是支付量约束, 在时期T内支付总量不超过承包商累积发生费用的一个比例β；式(7)表示所有支付的总和对于项目合同中的支付总额。约束(8)和(9)表示0-1变量；(10)表示支付量是一个连续变量。

客户的收益为使用软件项目带来的收益减去支付给承包商的费用。软件项目中客户的收益并非一次性获得，而是在软件系统使用期内逐步获得。客户第τ期的收益和费用根据资金的时间价值折算到参考点(t=0)，μ为年贴现率。从客户的角度建立无惩罚结构的优化模型：

(11)

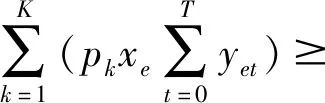
(12)

2.2 惩罚结构下的优化模型

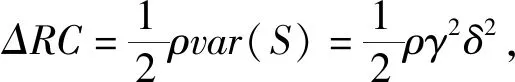
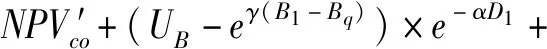
(13)

(14)

(13)是具有惩罚结构的承包商收益的目标函数，(14)是定义一个0-1变量Zq，当质量q=1时，其约束条件与目标函数(1)的约束条件相同。

在此情况下，由于客户是风险中性的，则其实际收益等于其期望收益，期望收益为:

(15)

(16)

(15)是具有惩罚结构时客户的目标函数。由于承包商的努力程度是私人信息, 客户无法对承包商的表现水平进行评价, 只有对软件产品的质量进行评价从而决定对承包商的奖惩。项目完成时若质量等级q>1,则在项目结束后客户向承包商支付时扣除部分款作为罚款。扣除部分为eγ(B1-Bq)。

2 算法设计

支付进度问题已经证明属于NP-hard问题，而具有惩罚结构的进度支付问题的求解更为复杂，在本文构建的组合模型中，确定最优支付进度需要确定三个变量序列：最优支付事件发生时间集合T*、最优支付量集合P*和质量等级集合Q*。启发式算法可成功的用于解决此类问题[12]。近年来，混合进化算法由于解决了大量的现实问题研发了极大的关注和兴趣。其中遗传算法(Genetic Algorithm, GA)因为具有优良的全局搜索能力被认为是解决该类问题最有效的算法。遗传算法是一种建立在一系列操作(选择、交叉、变异和改进)上的随机搜索方法和优化技术，其初始种群是随机产生的，并且其搜索方向采用按概率随机选择机制，因此遗传算法具有良好的全局搜索能力。禁忌搜索(Tabu Search, TS)是一个采用局部搜索方法进行数学优化的启发式算法，随机生成一个单一的解决方案，然后跳到这个解邻近的解，希望找到一个更好的解决方案。为提高局部搜索性能的技术，禁忌搜索算法采用记忆结构对访问过的解进行跟踪记录。如果一个解在一个特定的较短的时间内被访问过，那么该解将被标注成“禁忌”，不会被重复。因为记忆结构的原因，禁忌搜索避免了被困在局部最优的境况。本文设计了遗传算法和禁忌搜索算法的混合算法(GATS)对构建的模型求解，该混合算法采用遗传算法的基本结构，在父代个体交叉和变异时使用禁忌搜索的规则以增加种群的多样性，加快收敛速度。GATS算法的流程图如图1所示。

图1 GATS算法流图

算法中初始种群是随机产生的，采用轮盘法在配对库中选择一对个体作为父代。为降低近亲繁殖带来的种群多样性丢失和快速收敛的风险，采用禁忌表记录交配历史和家族号以区别染色体。当选择一对个体作为父代进行繁殖时，先检查交配的有效性。如果这对个体的家族号相同或者在禁忌表中存在，则生成一个邻解作为父代个体去产生后代。并将父代的两个个体插入禁忌表中，当禁忌列表超过预设限制时，将最前面的两个要素从禁忌表中移除，更新禁忌表。

4 算例分析

某企业因为信息化的需求要建设一个软件项目A，为节约成本和提高开发效率，企业选择将软件项目外包给专业软件公司去完成。假设该项目合同总价为U=78万元, 该软件项目的预计完成时间是30周。图1是一个采用AOA表示的某软件项目的活动网络图，每条弧上的数字代表了活动的序号。里程碑事件为{3,6,13,15}。活动费用在开始和结束时间之间按一定比例分配，分配比例η=0.6。项目双方约定价款分5次支付。为激励承包商保证项目质量以及弥补客户损失，客户在总价款中扣除一部分作为惩罚金，预留比例系数为ξ，则预留金额为UB=ξU。软件交付后根据对软件质量的评估结果来决定该部分金额的支付情况。软件质量从高到低分成三个等级q=1,2,3，对应承包商的3种表现水平，并且在三种质量等级下客户收益为Bq={120,100,90}。质量等级越低，扣款越多。1级为最高级，满足客户预期，这种情况下客户将预留款项UB全部付给承包商。客户对承包商的支付在项目开始时及里程碑事件处进行支付。本例中，承包商的边际利润率为π=18%，β=105%，贴现率α=0.0026,各项活动的工期和费用如表2所示。

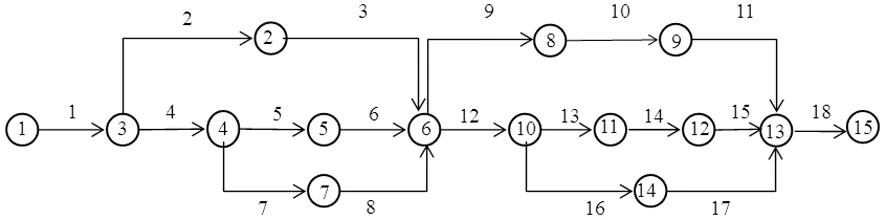
图2 某软件项目A网络图

表2 不同质量等级下软件项目各项活动的工期和费用

表3 软件项目A收益及支出的现金流量表

假设该软件系统预期使用5年，预计该系统运行后各年收益及支出(运行及维护费用)的现金流量如表3所示。

4.1 计算结果

首先由表2计算出各事件发生的时间窗, 取ε=0.001, 预留款比例ξ=0.05, 利用上述算法求得在不同质量等级，不同质量等级下项目的进度和双方收益如表4所示。

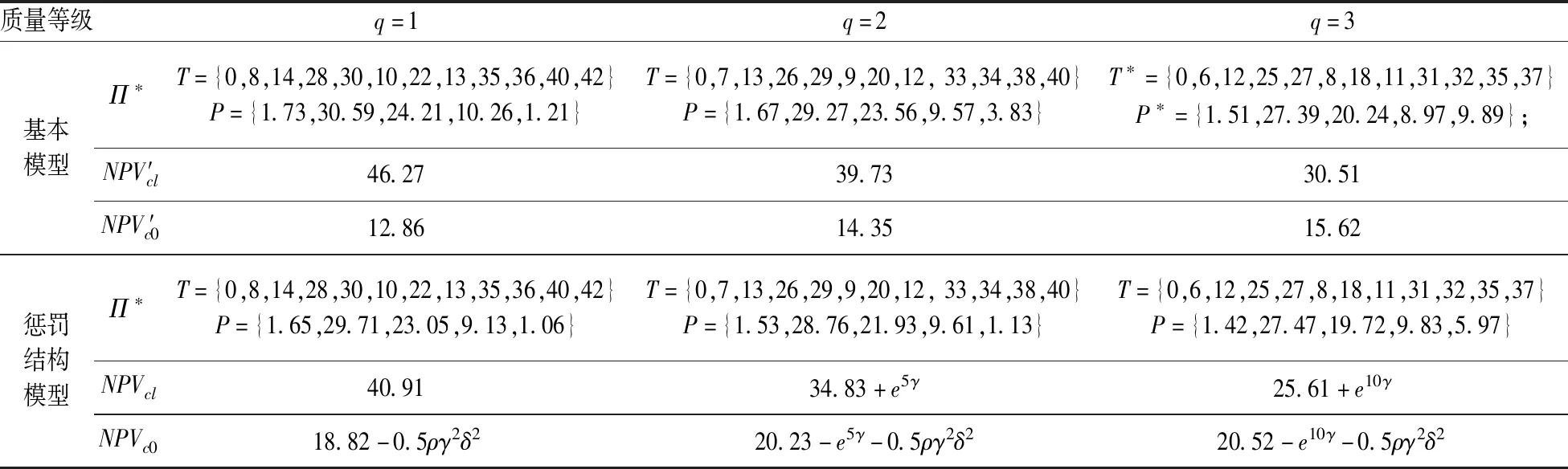
表4 不同质量等级下最优支付进度及双方收益

4.2 结果分析

表4显示了不同质量等级下的支付进度及双方的收益。从表4可看出, 在基本模型中, 质量等级较低时承包商花费的成本较低从而可获得较高的收益。这种情况下，当承包商交付的质量等级为1级时，客户获得最大收益为46.27，此时承包商获得的收益却最低，为12.86；而当承包商选择最低级(3级)的质量水平时，可获得最大的收益15.62，因此，承包商倾向于选择较差的能力程度以获取最大的收益，而此时客户的收益相对处于较低的状态，为30.51。当引入惩罚机制后, 因为惩罚系数γ的存在, 使得承包商不会贸然选择较差的表现水平。 只有当γ较低时, 承包商才会选择较差的表现水平, 且承包商的收益相对较高；反之，客户收益较低。

由表中数据计算出, 当γ≥0.07时, 承包商努力水平必须保持在使软件质量等级为1级的程度，才能获取较高的收益，此时，客户也获得最高收益40.91，即承包商与客户的偏好水平一致。反之，如果承包商降低努力程度, 虽然较低的努力水平能够使承包商较低成本, 缩短完工时间, 但因为惩罚结构的存在, 却并不能提高承包商的收益水平。当0.053≤γ≤0.07, 选择提供2级质量水平不会受到惩罚，会为承包商带来最大的收益。因此，承包商会倾向于选择2级质量水平。当γ≤0.053时, 惩罚机制不会起作用，承包商会选择质量水平3, 从而获得较高的收益，而此时客户的收益最低。因此, 较低的惩罚系数γ对承包商有益但对客户不利，无法起到激励承包商提高努力程度的作用。

此外，承包商最终实际收益还受到外部不确定性与风险规避态度有关，较高的外部不确定性和风险规避会增加承包商的风险成本，此时，承包商为提高收益也会偏向于选择较低的惩罚系数。

5 结论

本文在传统工程项目的支付进度模型的基础上, 建立了软件外包项目支付进度优化模型。 该模型反映了软件项目周期长、收益滞后性和分期获得性的特点, 以质量为激励因子, 构建了具有惩罚结构的承包商和客户的收益模型。 该模型用净现金流量作为双方的目标函数, 能够更准确地反映双方的真实收益。 并根据模型的特点设计了模型的求解算法, 最后利用一个数值算例对模型和求解结果进行了说明。本文的研究表明, 项目双方的收益与客户的支付行为、留置款比例及惩罚系数密切相关, 这对外包双方在合同签订时的谈判策略具有重要的借鉴意义。

本文以质量为激励因子研究了质量等级对项目支付进度的影响，并且以软件项目为例分别从承包商和客户的角度构建了项目支付进度模型。不仅是对项目支付进度问题的扩充和深入，也为软件项目支付进度问题的进一步研究提供了思路。但本文的研究还存在一些不足：首先，在构建的模型中未考虑通货膨胀的作用，但在软件项目实践中，由于许多项目持续的时间都较长，所以通货膨胀因素将对收益造成较大的影响；此外，为了可操作性在示例中将质量等级的分为三级，这种划分可能略显粗略。此外，本文考虑的是固价合同的支付情况，对于范围变更较大的情况，承包商往往不愿意接受固价合同方式，而倾向于选择时间材料合同，或者需要协商需求变动的价格支付。这些问题也是未来需要进一步研究的方向。