基于整数线性规划方法的舰载机航空保障资源优化调度

谭大力，王云飞，于连飞，朱承

1 海军研究院，北京100161

2 国防科技大学信息系统工程重点实验室，湖南长沙410073

3 中国人民解放军陆军边海防学院，新疆乌鲁木齐830001

0 引 言

航空母舰（以下简称“航母”）战斗力最直接的体现是架次率，即在规定时间内舰载机出动的架次数。为了分析影响架次率的主要因素，美军先后组织过多次大规模演习，其中，1997 年以“尼米兹”级航母战斗群为基础，进行了为期4 天的高强度演习，形成了2 份报告［1-2］。报告明确指出，舰载机的航空保障资源调度是制约架次率的关键因素之一。随着技术的进步，舰载机航空保障流程也在发生变化，美军还提出了“一站式”保障模式［3］。

目前，国内外已有一些针对舰载机航空保障流程分析和保障资源调度模型的研究。李梦龙等［4］以“尼米兹”级航母传统的多站式保障作为参考，对保障流程进行简化，将舰载机保障作业调度问题转换成车间作业调度问题，建立保障作业调度模型，并提出了一种改进的禁忌搜索算法来求解该模型。魏昌全等［5］根据不同出动方式下舰载机所需航空保障组织实施方式的区别，建立了舰载机的航空保障资源调度模型，即分波出动舰载机航空保障调度模型［6］和连续出动舰载机航空保障重调度模型［7］，并分别采用柔性流水车间调度和重调度的理论对这2种模型进行了研究。但在2个模型中，舰载机的航空保障过程都简化为了一系列的串行约束，降低了保障调度的难度，所以模型还需要进一步完善。岳奎志等［8］基于系统动力学理论，以舰载机在飞行甲板、机库、升降机之间转运与飞行后再次出动准备的保障任务为基础，建立了舰载机动态调运复杂时变系统的存量流量图与数学模型，并针对舰载机再次出动时挂弹与非挂弹2 种方案的舰载机动态调运过程进行了实例验证。

司维超等［9］在分析舰载机出动流程共性以及Petri 网优点的基础上，设计了一种面向任务的综合T-Petri 网模型，只是其模型中的模块比较简单，只能概略地对舰载机出动流程进行仿真。MIT 的Ryan 等［10］通过对一款名为甲板运作行动过程规划者（Deck operation Course of Action Planner，DCAP）的辅助飞行甲板管理软件的开发，研究了反向强化学习方法［11］和基于排队网络的策略［12］，优化了在舰载机自适应多阶段调度问题中的应用，并通过甲板作业仿真，将基于整数线性规划模型的优化算法与传统的专家启发式规则进行了调度性能上的对比［13］。

目前类似的研究中，较少考虑单机保障流程和波次多机保障流程的特点，即使在生产调度领域，比如车间作业调度等，也很难找到相同特点的流程，因此基于以上特点考虑保障资源的调度，不但有助于提高航母的架次率，而且在此基础上的资源调度方法研究也对调度问题的理论研究进行了拓展。

为此，本文将考虑按波次起飞时多种类型舰载机的起飞顺序，以及对单架舰载机保障过程中保障任务之间的执行顺序要求，以最小化保障一波次舰载机所需的时间为目标，建立多类型舰载机航空保障资源调度模型，并对模型进行求解，然后以“福特”级航母舰载机航空保障流程为例，验证模型的准确性。

1 舰载机典型出动模式的出动特点及航空保障流程分析

舰载机航空保障流程是一个复杂而严密的过程。舰载机类型多样，机群典型出动模式具有以下特点：

1）不同类型舰载机的保障需求和航空保障流程存在较大差异，例如直升机不需要弹射起飞保障，预警机不需要挂弹保障，而战斗机则两者都需要；

2）航空保障作业流程中涉及任务之间的执行顺序包括串行、并行和柔性关系；

3）执行一项机群波次作战任务时，起飞出动的舰载机通常有多种类型，包括勤务直升机、预警机、护航战斗机和执行任务战斗机等，且各舰载机起飞也存在严格的先后顺序，例如预警机需要比执行任务的战斗机先起飞。

上述特点会给保障资源的调度带来重要影响，因此在建模时需要考虑上述特点。

考虑到“一站式”保障设置是未来航母普遍采用的保障样式，本文基于“一站式”保障模式开展研究，即舰载机着舰后自行滑入甲板保障站位，在同一站位上完成所有保障作业后，再滑出站位转入起飞。“福特”级航母单机保障的流程如图1 所示。其中：有些任务有严格的先后顺序，例如必须先进行军械检查才能进行挂弹，这种任务关系称为串行关系，需要在一个任务之前先执行的保障任务称为该任务的紧前任务；有些任务可以同时进行，例如加电和通风，这种任务关系称为并行关系；还有些任务不能同时进行但是没有严格的先后顺序，例如充氧和加油不能同时进行，但是具体的先后顺序没有要求，这种任务关系称为柔性关系。在机群按波次出动的情况下，还需要考虑不同舰载机的起飞顺序，称为舰载机的优先权，优先权高的舰载机要先于优先权低的舰载机起飞。以上特点都会对保障资源的调度产生重要影响。

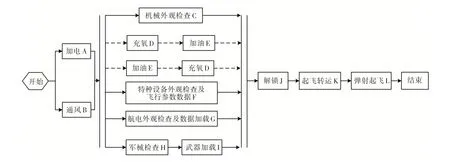
图1 单机保障流程图Fig.1 The flow chart of single-carrier aircraft maintenance

在“一站式”保障中，航空保障资源以保障小组为单位对舰载机进行保障，每个保障任务都有多个保障小组，并且保障小组不固定保障某一特定舰载机，可以对所有类型的舰载机进行相应任务的保障，由于训练效果不同，其完成保障的时间也有所区别。

2 航空保障作业流程整数线性规划模型构建

本文旨在建立一个可指导不同型号航母舰载机航空保障资源调度的通用优化模型，该模型的输入为：舰载机的起飞顺序、舰载机航空保障流程中各任务之间的串行、并行和柔性关系，以及舰载机航空保障资源的数量和保障能力；输出为优化的资源调度方案。建立的模型应为适用于不同型号航母的普适性模型，通过调整模型的输入，可以对不同型号航母舰载机的保障资源进行优化调度。为建立该模型，先给出模型想定如下：

1）优先权假设：不同类型舰载机的起飞顺序不同，优先权较高的舰载机先起飞。

2）航空保障资源以保障小组为单位进行。

3）每个保障小组在任一时刻只能保障一架舰载机。

4）不同保障小组保障同一任务所需时间可以不相同。

5）一架舰载机的一个保障任务只接受一个小组保障。

6）保障任务之间实行快速无缝转换，转换时间忽略不计。

根据以上分析和想定，对舰载机航空保障资源进行调度需要考虑2 个方面的内容：一是对需要保障的所有舰载机的保障任务进行排序，并为每个任务分配合适的保障小组；二是根据舰载机类型的不同，考虑起飞优先权给资源调度带来的影响。下面，将对航空保障资源调度的目标和约束进行抽象，建立航空保障资源调度模型。

多类型舰载机航空保障建模的目标是获得使一波次所有舰载机起飞时间最短的资源调度方案，可得到目标函数为：

式中，Cmax为所有舰载机的保障完成时间，min。式（1）表示目标函数为使所有舰载机的保障完成时间最短。

每架舰载机的每个任务只需要一个保障小组进行保障，可得

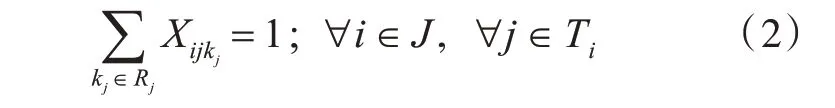
式中：J为舰载机集合；i为舰载机的编号（i∈J）；j为任务的编号（j∈T），T为任务集合；Ti为舰载机i包含的任务集合；Rj为可以保障第j个任务的保障小组集合；kj为可以保障第j个任务的保障小组编号（kj∈Rj）；Xijkj为决策变量，表示保障小组与保障任务的对应关系，如果保障小组kj保障任务Tij，Xijkj取值为1，否则Xijkj取值为0。

每个保障小组在任意时刻只能保障1 架舰载机，用下式表示：

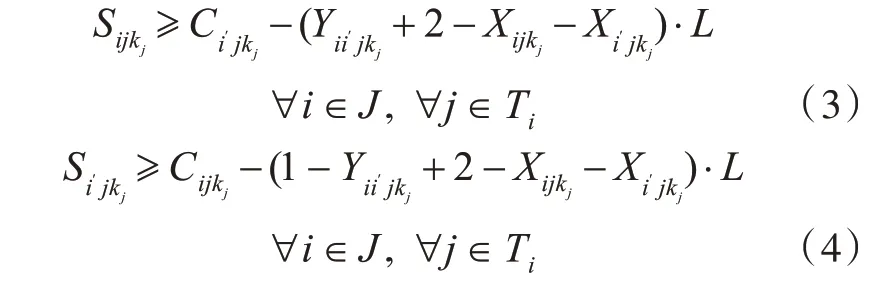
式中：i′为与i 不同的另外舰载机的编号(i′∈J)；Sijkj为非负决策变量，表示保障小组kj开始保障任务Tij的时间，min；Cijkj为非负决策变量，表示保障小组kj结束保障任务Tij的时间，min；Yii′jkj为决策变量，如果保障小组kj保障任务Tij先于任务Ti′j，Yii′jkj取值为1，否则取值为0；L为一个足够大的正实数。

对每个任务的保障时间需要达到一定时长，用下式表示：

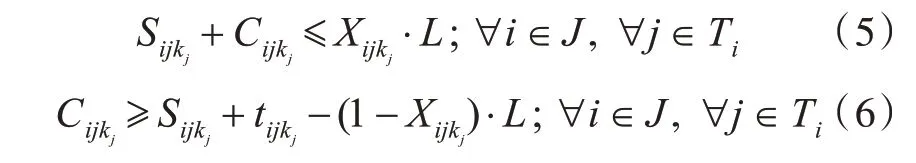
式中，tijkj为保障小组kj保障任务Tij所需要的时间，min。

舰载机任务之间的串行关系为

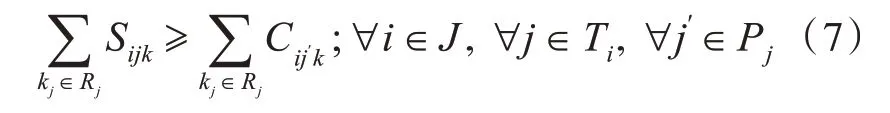
式中，Pj为任务j的紧前任务集合。

舰载机任务之间的柔性关系为

式中：Fj为任务j的柔性任务集合；Zijj′为决策变量，如 果 舰 载 机i的 任 务j先 于 任 务j′保 障（j′∈Fj），Zijj′取值为1，否则取值为0。

舰载机的起飞优先权为

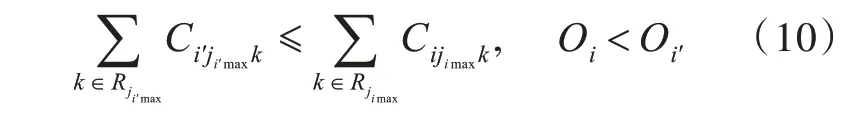
式中：Oi为舰载机i的优先权，优先权大的舰载机先起飞；jimax为舰载机i最后一个任务的编号。

Cmax为所有舰载机都完成保障的时间：

得到完整的航空保障资源调度模型如下：

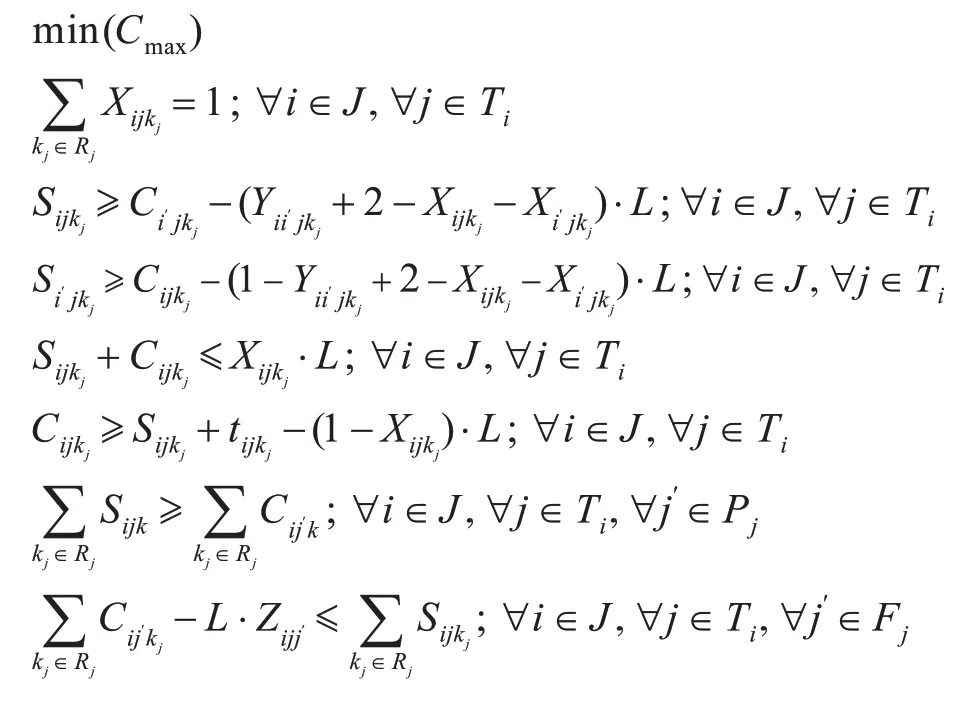
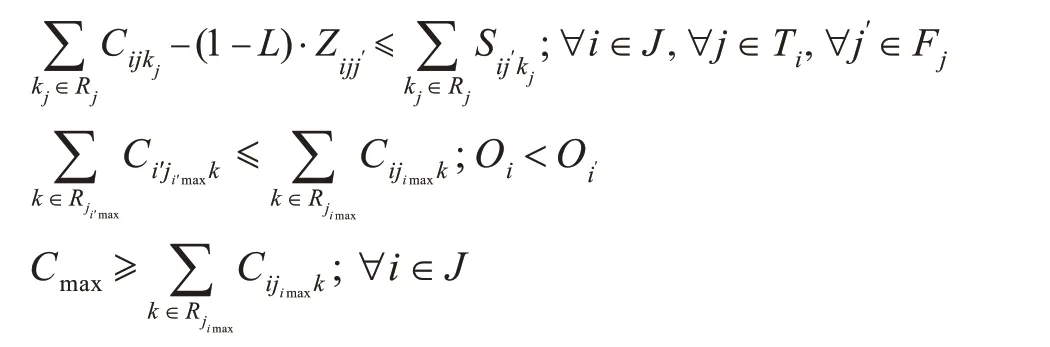
根据对变量的描述和约束的表达方式可以看出，以上建立的模型为混合整数线性规划模型。

3 CPLEX 和改进的差分进化算法求解

混合整数线性规划是整数规划的一种类型，不同于一般的线性规划问题，整数规划和0-1 规划至今尚未找到一般的多项式解法。对于整数规划问题的求解，在可行域有界的情况下最容易想到的是穷举法，但对于大规模问题，穷举法的计算时间过长。除了穷举法，最典型的方法是分支定界法和割平面法，这2 种方法的思想类似，都是将整数规划问题转化为一系列非整数规划问题，通过不断的求解和衍生子问题，逐渐减小解空间并不断向最优解靠近。现在大部分整数规划商业软件，包括CPLEX，LINGO 和BARON 等都是基于分支定界框架的。随着计算机技术的发展，智能优化算法在求解优化问题上的应用越来越多。本文选取IBM ILOG CPLEX 的混合整数线性规划求解器cplexmilp 和 改 进 差 分 进 化 算 法［14］（Improved Differential Evolution with Local Search，IDELS）来对模型进行求解。

CPLEX 可用来求解线性规划（LP）、二次方程规划（QP）、带约束的二次规划（QCQP）和二阶锥规划（SOCP）等4 类基本问题，以及相应的混合整数规划（MIP）问题。该软件有自带的语言，简单易懂，同时与众多优化软件及语言兼容（与C++，Java，Excel，Matlab 等都有接口），可以较容易地通过这些语言调用CPLEX 优化引擎进行问题求解。对于处理数百万个约束和变量的大规模问题，有非常快的运行速度和较好的求解优势，求解速度持续刷新了解决数学规划问题的最高记录，可以解决许多现实中的大规模问题。CPLEX 的混合整数线性规划求解器cplexmilp 可以直接用于整数线性规划模型的求解。在求解过程中，只需将标准模型的目标函数和约束条件中各个决策变量的系数以及资源约束向量作为cplexmilp 求解器的输入参数，并输入舰载机航空保障流程决定的任务关系等其他初始参数，即可利用cplexmilp求解器自动求解。

差分进化（Differential Evolution，DE）算法是由Storn 和Price 共同提出的一种采用浮点矢量编码在连续空间中进行随机搜索的优化算法。Yu等［14］提出对差分进化算法进行改进用于求解舰载机航空保障资源调度问题，主要对差分进化算法的编码、解码、变异规则进行改进并结合了局部搜索算法，改进的差分进化算法用IDELS 表示，其算法流程图如图2 所示。

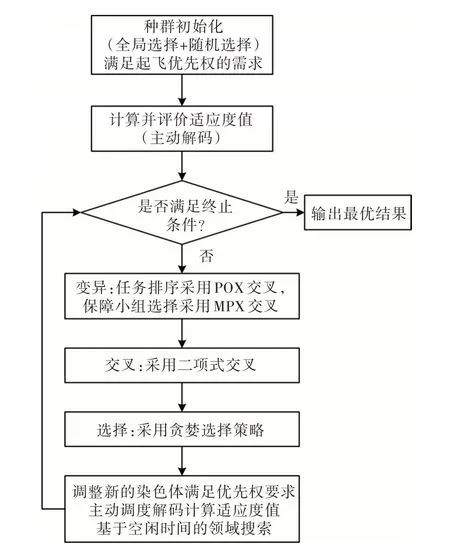
图2 IDELS 算法流程图Fig.2 Flow chart of IDELS algorithm

4 仿真计算

本次实验平台的计算机的配置为Intel（R）Core（TM）i7-4790 CPU@3.6 GHz，16GB 内 存，Windows 7.0 操作系统。

由于没有标准测试集可供调用，为完成仿真实验，以美军最新的“福特”级航母为背景，其战斗机的航空保障流程如图1 所示。根据图1，可以得到任务之间的串行、并行和柔性关系，例如“军械检查”和“武器加载”是串行关系、“加电”和“通风”是并行关系、“充氧”和“加油”是柔性关系。想定以下测试场景：

1）舰载机的类型有5 种：勤务直升机1 架、预警机1 架、护航战斗机1 架、反潜机1 架、战斗机4～12 架，所有类型的舰载机可以在甲板上同时开始保障。

2）舰载机的起飞顺序为勤务直升机（编号：1）、预警机（编号：2）、护航战斗机（编号：3）、反潜机（编号：4）、战斗机。根据任务强度不同，起飞的数量也不同，假设有以下5 种出动场景：

场景1：4 架战斗机，编号5～8；

场景2：6 架战斗机，编号5～10；

场景3：8 架战斗机，编号5～12；

场景4：10 架战斗机，编号5～14；

场景5：12 架战斗机，编号5～16。

3）假设所需舰载机都已在甲板，除直升机、预警机不需要挂弹，直升机不需要弹射起飞外，其他舰载机的保障流程相同，都有12 个任务（A～L），如图1 所示。

4）共有30 个保障小组，每个小组可以保障的任务及所需时间（时间单位：min），如表1 所示。

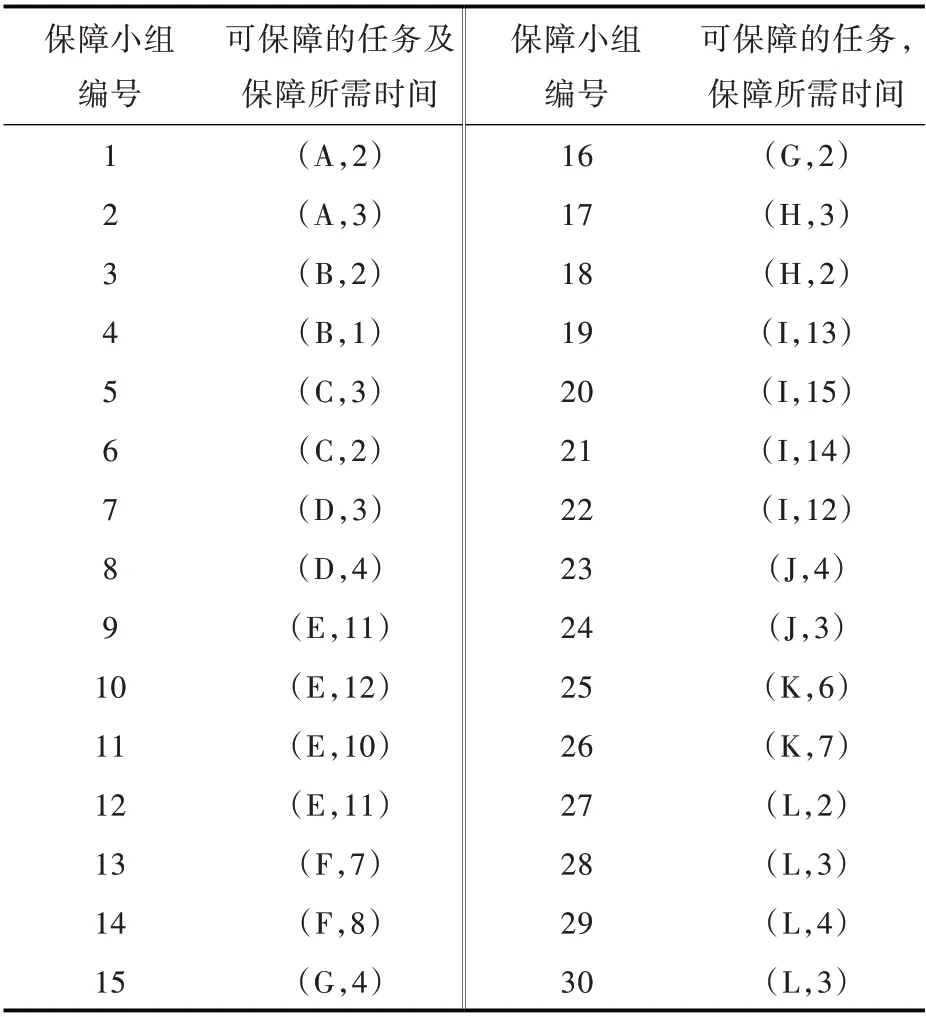
表1 每个保障小组可以保障的任务及持续时间Table 1 Process and duration of each group

将上述想定的舰载机航空保障流程结构、舰载机机群的数量和起飞顺序，以及保障小组的保障能力作为初始输入数据，将12 个保障任务分别编号A～L，则根据保障流程结构即可得到T，Pj和Fj的输入值；根据保障小组的数量和保障能力，可以得到R和tijkj的输入值；根据舰载机起飞顺序，可以得到Oi的输入值。本文算法在Matlab 2014（a）中编程实现，设定差分进化算法的参数为：缩放因子F=0.5，交叉概率CR=0.9，种群规模NP=100，最大迭代次数Gmax=400，在每种场景下对改进的差分进化算法进行20 次计算，取20 次计算结果的平均值，并记录IDELS 迭代400 代所需的平均时间；cplexmilp 的算法运行时间设置为与改进的差分进化算法相同，其余参数采用cplexmilp 的默认值。得到不同算法计算出的保障一波次所需时间以及算法运行时间如表2 所示。表中第1 列表示5 种不同场景下的舰载机数量，第2 列表示IDELS 迭代400 代所需的平均时间，也即cplexmilp的运行时间，第3 列和第4 列分别表示IDELS 和cplexmilp 的计算结果。由于2 种计算方法的运行时间相同，根据表2 中的计算结果，2 种计算方法的计算精度和收敛速度各有优劣，在设定的5 种场景下，cplexmilp 的计算结果比IDELS 的计算结果优，但随着出动舰载机规模的增大，计算结果间的差别在逐渐缩小，这是因为IDELS 求解的收敛速度虽受问题规模影响较小，但是易陷入局部最优，而cplexmilp 求解的收敛速度受问题规模影响较大。因此，如果需要在较短时间内得到可以接受的较优资源调度方案，可以选择IDELS 进行求解；如果要求得到尽可能好的资源调度方案，可以选择cplexmilp 进行求解。

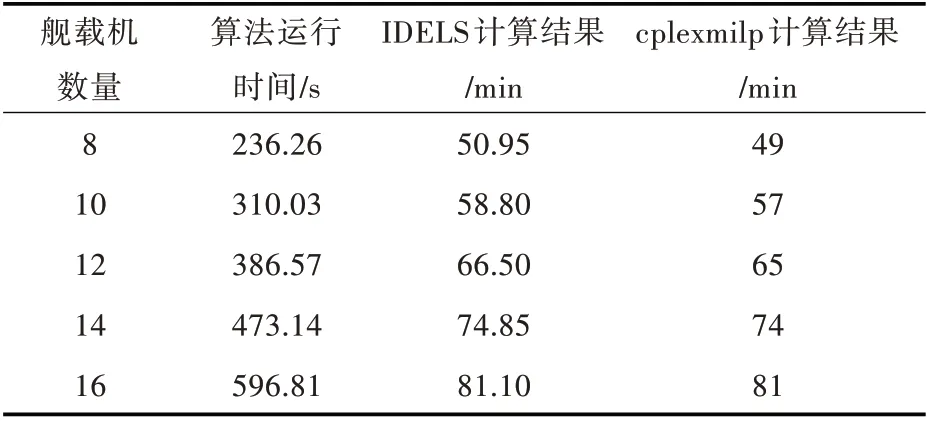
表2 改进的差分进化算法与cplexmilp 求解结果对比Table 2 Comparison of IDELS and cplexmilp

根据cplexmilp 求解得到的保障一波次16 架舰载机的资源调度甘特图如图3 所示。图中不同颜色的矩形条表示不同舰载机，矩形条中代号组成为：舰载机编号+任务编号，例如图3 中右上角的矩形条“8L”表示第8 架舰载机的第L 个任务由第30 个保障小组从78 min 开始保障至第81 min结束。从图中可以看出决策变量的取值：保障每架舰载机的每个保障任务的保障小组编号及其保障的起始时间，保障全部16 架舰载机所用时间与美军航母甲板波次舰载机保障作业周期通常采用的1.5 h（90 min）基本吻合。通过对比每个保障任务的开始时间和结束时间可以看出，资源调度方案符合舰载机航空保障流程中保障任务之间的执行顺序、舰载机的起飞顺序以及保障小组的数量和保障能力约束，说明了本文建立的资源调度模型的正确性，该资源调度模型可以用于指导航空保障流程中的资源优化调度问题。

5 结 语

图3 保障资源调度甘特图Fig.3 Gantt chart of resource scheduling

本文分析了“一站式”保障模式下多类型舰载机航空保障流程中不同舰载机的起飞顺序，每架舰载机的保障任务之间的串行、并行和柔性关系；基于整数线性规划方法建立了舰载机航空保障资源调度的混合整数线性规划模型，模型的输入为：舰载机的起飞顺序、舰载机航空保障流程中各任务之间的串行、并行和柔性关系以及舰载机航空保障资源的数量和保障能力；输出为优化的资源调度方案；是一个可应用于不同型号航母的舰载机资源优化调度模型。利用cplexmilp 和IDELS 对模型进行了求解。以美军“福特”级航母舰载机航空保障流程为例进行了仿真计算，验证了模型的准确性，本文建立的模型可用于指导舰载机航空保障资源的优化调度。两种求解方法存在计算精度和收敛速度上的差异，求解时具体选用哪种方法需根据出动规模以及对求解时间和精度的要求来确定。