基于动柔度方法的管路动力吸振器设计研究

张琳，李华峰，陈勇，张涛*，丁杨建

1 华中科技大学船舶与海洋工程学院，湖北武汉430074

2 武汉第二船舶设计研究所，湖北武汉430205

0 引 言

目前，载流管路作为输送流体的重要载体已被广泛应用于船舶、汽车等相关领域。而载流管路在泵或者其他设备的激励作用下会产生振动，影响管路上的精密仪器稳定工作，对管路安全构成威胁，所以针对载流管路的减振研究成为了学术和工程界的重要课题［1］。

动柔度矩阵（Receptance matrix）用于表示结构某节点各个自由度在单位力激励作用下的运动量的大小，其中运动量包括位移、速度和加速度。动柔度方法（Receptance Method）是一种利用结构的频响函数对系统进行减振分析的方法。该方法以系统结构的动柔度矩阵为基础，通过被动修改或者主动控制修改结构的质量、刚度或阻尼矩阵，从而达到控制振动的目的。运用该方法时，若结构简单，可根据模态理论建立结构的数学模型，得到结构的动柔度矩阵；若结构复杂不易建模，则可通过试验测量关注点在一定激励作用下的响应函数，得到该点的动柔度矩阵。因此，动柔度方法在分析大型复杂结构振动时具有明显的优点。运用该方法，在分析过程中无需针对复杂的结构进行精确的有限元建模，也无需分析确定振动的激励源，故可满足实际工程中的经济性、快捷性需求。运用动柔度方法对结构进行振动控制主要有被动修改和主动控制2 种方法，其中应用最广泛的是被动修改法。

在结构被动修改方面，早在1968 年，Weissenburger［2］在其研究工作中就使用了秩为1 的动柔度矩阵来修改结构的模态参数，配置结构的固有频率。Pomazal 和Synder［3］将文献［2］所述方法扩展到弹簧阻尼系统，计算得到了该系统的固有频率和振型。1972 年，英国在直升机设计制造中运用动柔度方法进行了结构零点配置。Vincent［4］研究发现，当某个受固定频率的外载荷激励的系统被修改时，系统其他频率点的响应将随着修改参数的变化在复平面上呈现出一个圆，由此将系统在物理上的减振问题简化为了在复平面圆上寻找离原点最近频率点的数学问题。Berman 和Nagy［5］进一步研究了Vincent 的复平面圆理论，提出了由弹簧质量系统组成的吸振器。Tehrani等［6］将Vincent的复平面圆理论扩展到了对典型的弹簧阻尼系统的不同位置进行修改，从而达到抑制所关注频率点的振动的目的。然而，该理论仍有一定的缺陷，即在结构被动修改后会导致原始结构中未参与修改的其他固有频率发生变化，这种改变可能导致其他位置的振动变大等其他不良后果。鉴于此，Belotti 等［7］提出了一种特殊的质量弹簧系统，利用该系统对结构的部分固有频率进行配置时，几乎不影响结构的其他频率。

Frahm［8］于1909年提出的动力吸振器（Dynamic Vibration Absorber，DVA）是一种典型的结构被动修改形式，其可用来吸收主系统在某个频率点的振动能量，从而达到结构减振的目的。动力吸振器由质量块、弹簧和阻尼器组成。该吸振器可被视为一个附加在需要减振的主结构上的单自由度系统，当主体结构受到激励产生振动，且激励频率接近于吸振器的调谐频率时，吸振器将被动地在主体结构上施加一个反作用力，以抵消外部激励力。吸振器在工作状态下，外界激励的能量会被传递到吸振器上，从而避免了主体结构因振动而受到破坏。针对动力吸振器的减振效果，任意［9］在分析多种调谐质量阻尼器的基础上，发现采用多个调谐方式的减振效果最好，并通过试验对管路上应用调谐质量阻尼器的减振效果进行了验证。

综上所述，动力吸振器具有结构简单、安装方便、无需求解数学模型的优点，在管路减振研究中具有很好的应用前景。因此，本文将基于动柔度法中的被动修改理论，推导得出利用弹簧质量系统对多自由度系统进行被动修改后的动柔度矩阵，并利用弹簧质量系统增加的自由度，对原多自由度系统中的目标自由度进行零点（反向共振点）配置，使该自由度下的振动得到相应的抑制。在此基础上，设计一种应用于载流管路上的动力吸振器，并通过试验验证理论的有效性，研究其减振效果。

1 结构修改的弹簧质量系统

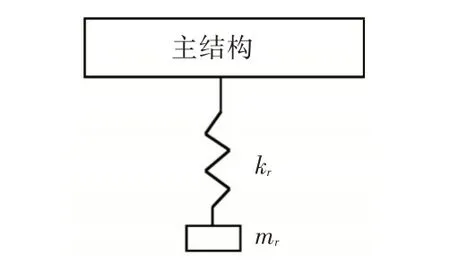
图1 利用弹簧质量系统修改主结构第r自由度示意图Fig.1 Schematic diagram of the r-DOF main structure modification using a spring mass system

由上文可知，动力吸振器本质上是一种附加在主结构上的弹簧质量系统。假设主结构为一个多自由度系统，且吸振器附加在该多自由度系统的第r 自由度（节点）上，如图1 所示。图中，mr为吸振器质量，kr为吸振器弹簧刚度。动力吸振器工作时会产生竖向运动，从而增加了整个系统的自由度。因此，若原结构的自由度为n，附加了吸振器后的结构的自由度则为n+1。

由模态理论可知，受迫振动的多自由度系统的运动微分方程为

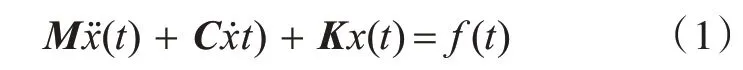
式中：M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；x为结构的位移；f(t)为施加到第q 自由度上的载荷，t为运动时间。

对式（1）进行拉氏变换，可得

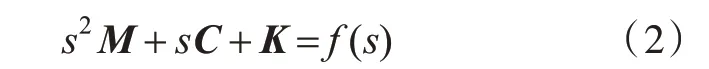
式中，f(s)为系统受到的外界激励，其中s为结构的复频率。

将系统的动刚度矩阵Z(s)定义为

式（2）可表示为

式中，x(s)为系统受到激励后的运动量（位移、速度、加速度）。

将式（4）写成如下矩阵形式：

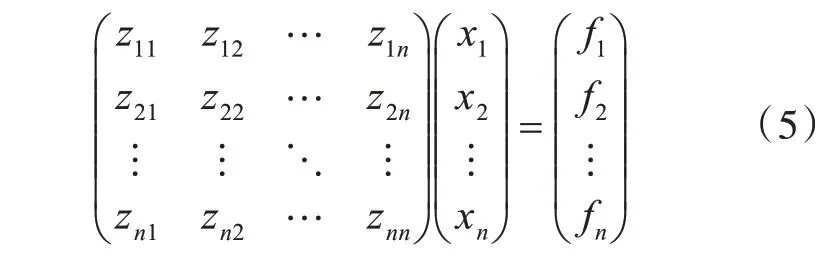
式中：zij为多自由度系统在第i 自由度上产生的单位运动量需要在第j 自由度上施加的激励；xi为第i 自由度的运动量；fi为外界在第i 自由度上施加的激励。

假设多自由度系统的自由度为n，则在系统的第r 自由度上附加弹簧质量系统后，式（5）可表示为

式中：等号左侧为多自由度系统在增加弹簧质量系统后动刚度矩阵与各自由度上的运动量的积，其中系统的新动刚度矩阵为原动刚度矩阵增加了一行及一列0 元素；等号右侧为弹簧质量系统对结构的修改与外力向量之和；dx 为系统附加的弹簧质量系统在外界激励作用下的运动量；ω为多自由度系统第r自由度的固有圆频率。

为了消去附加弹簧质量系统后多自由度系统额外增加的自由度，提取式（6）最后一行：

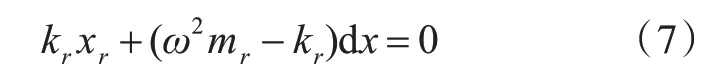
则dx 可表示为

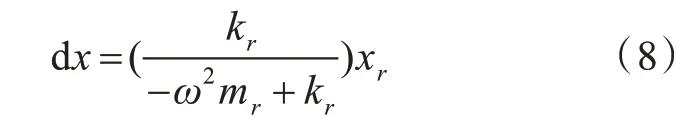
式中，xr为系统在第r自由度结构的位移量。

将式（8）代入式（6）中，则式（6）等号右侧可写为

提取式（9）中第r行，可得

式中，fr为外界在第r自由度施加的激励。

将式（10）再代入式（6），并消去式（6）的第n+1行及n+1 列，可得

式（11）中的动刚度矩阵与结构修改前的动刚度矩阵具有相同的维度。这里，定义式（11）中等号两侧同时左乘原系统的动刚度矩阵的逆Z(s)-1为动柔度矩阵H(s)，来表示单位作用力下运动量的大小，其表达式为

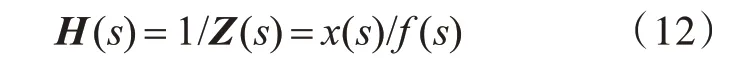
因此，将式（11）中的等号两侧左乘动柔度矩阵H(s)并移项，可得

简化式（13），可得

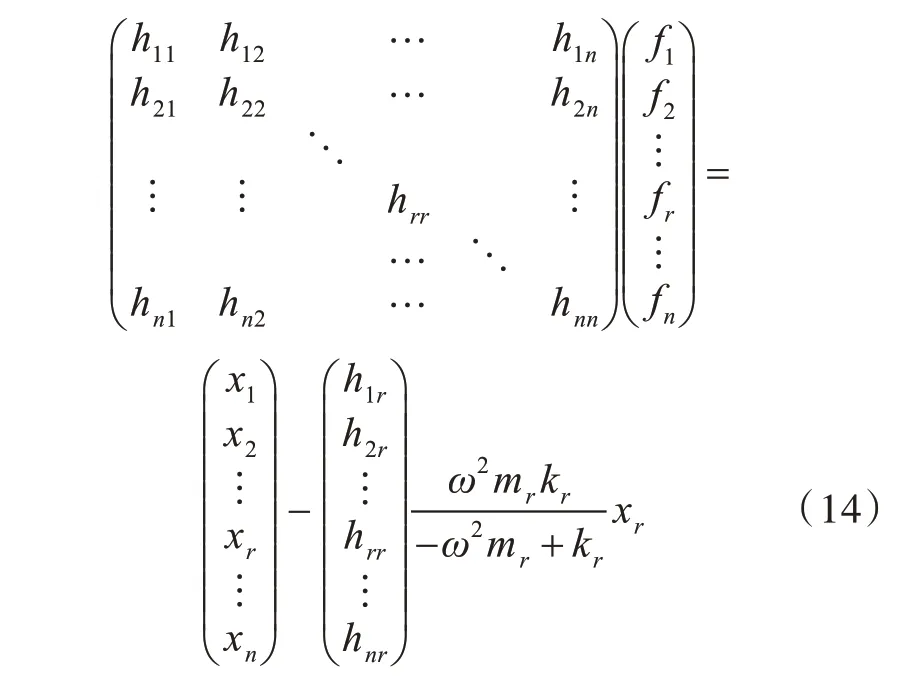
提取式（14）第r行，可得

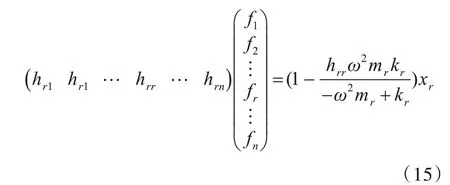
式（15）也可写为

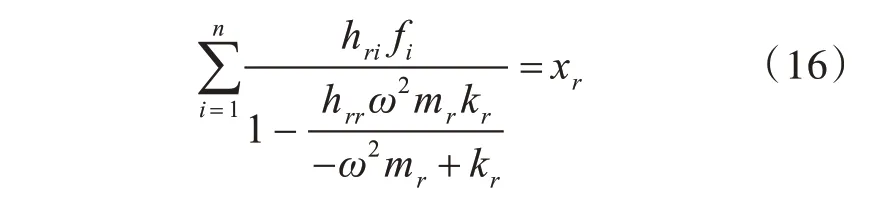
式中，hri为第r 自由度施加单位激励下，在第i 自由度的位移；hrr为在第r 自由度施加单位激励下第r自由度的位移；fi为在第r自由度施加的外力。

由式（16），可得附加了弹簧质量系统后系统的动柔度，即

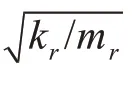
若考虑附加的吸振器中存在阻尼项cr，则按照以上推导，式（17）可写为

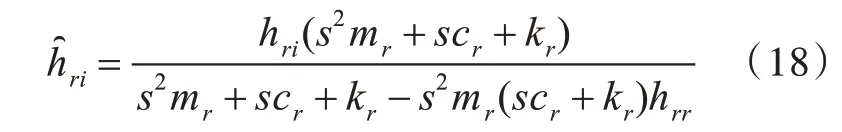
令式（18）右侧分子hri(s2mr+scr+kr) =0，则由式（19）可确定系统增加的零点。

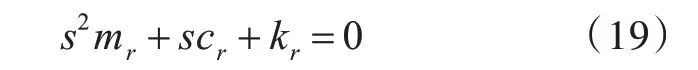
式（19）与计算单自由度阻尼系统振动频率的特征方程相同，其解为

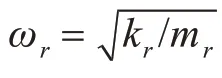
2 管路动力吸振器设计

根据上节的结论，本文设计了一种用于载流管路减振的动力吸振器。该吸振器将2 组弹簧质量系统安装在管路某节点的同一自由度上，以吸收该节点上2 个频段的外界激励能量。

2.1 动力吸振器的三维模型

由于载流管路的结构形状为圆柱形，本文将动力吸振器的安装结构设计为环形，并将用于吸振的弹簧质量系统附加在柱形结构上，如图2 所示。此吸振器具有安装拆卸方便及适用范围广的特点。

图2 管路动力吸振器模型Fig.2 Model of the dynamic vibration absorber for pipeline

图2 中的环形安装结构为吸振器的安装结构和弹簧质量系统的支撑结构。为了减少不用于振动能量吸收的附加质量，环形安装结构采用密度较小的塑料制造，而质量块则采用密度较大的钢材制造。根据文献［11］的研究结论，质量块与主结构的质量比越大，减振效果越好。但为了不大幅度增加管路结构的负载，质量块的质量应为管路两端的支撑内部结构（节点10 到节点11 的管路段，参见图5）质量的1/30～1/10［12］。吸振器的刚度由弹簧提供，其弹性系数可根据管路的目标减振频率确定。

2.2 动力吸振器的安装

选取工业领域常用的典型复杂载流管路，并通过载流管路的振动实验研究动力吸振器对典型载流管路振动特性的影响。典型载流管路的实验模型如图3 所示，其各项物理参数见表1。

图3 典型载流管路的实验模型Fig.3 Experimental model of a typical fluid-conveying pipeline

本文设计的动力吸振器安装结构采用3D 打印技术制造，如图4 所示。根据管路尺寸，确定环形安装结构的内径为25 mm，厚度为5 mm，而动力吸振器的质量参数与弹簧弹性系数根据载流管路的目标减振频率确定。实验中，将吸振器安装在载流管路节点10 与节点11 之间的中间位置（定义该位置为节点r），与节点11 的间距为300 mm，如图5 所示。实验中，复杂载流管路中注满水，设流体流速为0（静水），采用激光位移传感器测量节点r处的位移。用力锤或者激振器激励节点11，得到节点r处的动柔度曲线如图6～图8 所示。

表1 载流管路物理参数Table 1 The physical parameters of fluid-conveying pipeline

图4 管路动力吸振器实物图Fig.4 The physical photo of dynamic vibration absorber for pipeline

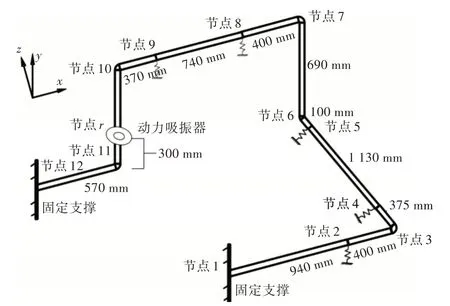
图5 动力吸振器安装位置示意图Fig.5 Diagram of installation position for the dynamic vibration absorber

3 结果分析

3.1 动力吸振器的作用

实验中，测量得到载流管路在未安装动力吸振器时的动柔度曲线，如图6 中的蓝色曲线所示。由图6 可以看出，载流管路在8.85 Hz 时的动柔度最大，而根据式（13）中动柔度的定义可知，动柔度越大，管路的振动越大，故为了减小管路8.85 Hz 处的振动，取动力吸振器中质量块的质量mr1=0.1 kg，弹簧刚度kr1=(2πf1)2mr1= 394.78 N/m（f1为弹簧质量系统的频率）。通过振动实验，测量得到载流管路在安装动力吸振器后节点r 处的动柔度曲线，如图6 中的红色曲线所示。

由图6 可见，根据原结构动柔度曲线配置动力吸振器的质量与刚度参数后，节点r处的动柔度曲线在8.85 Hz 处出现了一个零点，即反向共振点。这说明吸振器较好地吸收了8.85 Hz 附近频带的振动能量，且在其他频率下未出现较大的尖峰。这说明，本文设计的吸振器可有效抑制管路在节点r处的振动。

3.2 附加两个弹簧质量系统的动力吸振器

由图4 可以看出，本节在3.1 节的动力吸振器中增加一个弹簧质量系统，使动力吸振器配置2个弹簧质量系统，用以吸收管路节点处2 个频带的振动能量。为研究吸振器的吸振效果，设定管路的目标减振频率为10 和20 Hz，配置吸振器上2 个弹簧质量系统的各项参数为：mr1=0.1 kg，kr1=(2πf1)2mr1=394.78N/m；mr2=0.1kg，kr2=(2πf2)2·mr2=1 579.14 N/m。通过实验，测量得到附加新的动力吸振器后节点r处的动柔度曲线如图7所示。

由图7 可见，在节点r 处安装附加2 个弹簧质量系统的动力吸振器后，节点r 的动柔度曲线上10 和20 Hz 处分别出现了一个零点，这说明新安装的动力吸振器较好地抑制了节点r 在10 和20 Hz 附近的振动。

图7 安装附加2 个弹簧质量系统的吸振器后管路节点r处的动柔度传递曲线Fig.7 Receptance at the node r attached the vibration absorber with two spring mass systems

3.3 不同参数的吸振器的吸振效果对比

本文给出了3 种不同参数（质量块质量mr与弹簧刚度kr）的动力吸振器，以探究吸振效果。表2 给出了3 种吸振器的参数。

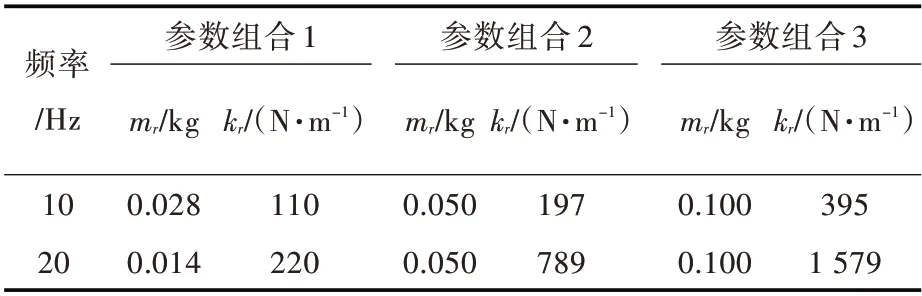
表2 不同参数的吸振器Table 2 Vibration absorber at various parameters

图8 所示为安装了不同参数的动力吸振器后节点r 处的动柔度曲线。由图8 可见，对于相同的目标减振频率，使用质量、刚度更大的弹簧质量系统可以增加减振频带，但附加了弹簧质量系统的自重会造成新的振动尖峰。因此，需要综合考虑动力吸振器的设计参数。

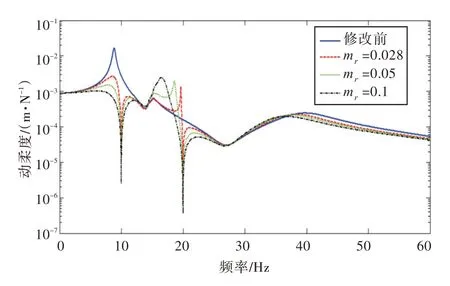
图8 安装不同参数的吸振器后管路节点r处的动柔度传递曲线Fig.8 Receptance at the node r of the vibration absorber with various parameters

4 结 语

本文根据结构被动修改理论，设计了一种应用于载流管路上的动力吸振器，推导得出了利用弹簧质量系统对多自由度系统的动柔度矩阵进行被动修改的理论过程，并通过零点配置实现了对多自由度系统在某自由度下的振动抑制。在管路振动实验中，通过配置动力吸振器的弹簧质量系统的质量参数及刚度参数，使吸振器较好地抑制了管路在目标减振频率下的振动。

通过对比3 种不同参数动力吸振器的吸振效果，发现其调谐质量越大，吸振频带越宽，减振效果越好。