基于波动理论的共振转换器减振特性分析

李良伟，赵耀

1 中国人民解放军92942 部队，北京100161

2 华中科技大学船舶与海洋工程学院，湖北武汉430074

0 引 言

共振转换器（Resonance Changer，RC）作为一种振动控制装置，早在文献［1］中已被提到。该装置的概念模型如图1 所示，其减振方式主要是将流体作为减振介质，在外部激励下能够同时产生流体的惯性力、沿程阻尼力和流体弹性力，进而改善原系统的振动特性，其主要特点是在满足静载荷稳定传递的同时能有效控制脉动激励力。图1中，xb和x1分别为推力轴承和共振转换器的纵向响应位移，L1为外接管系长度，A0为活塞截面积，A1为外接管系截面积，V1为外接腔体体积。

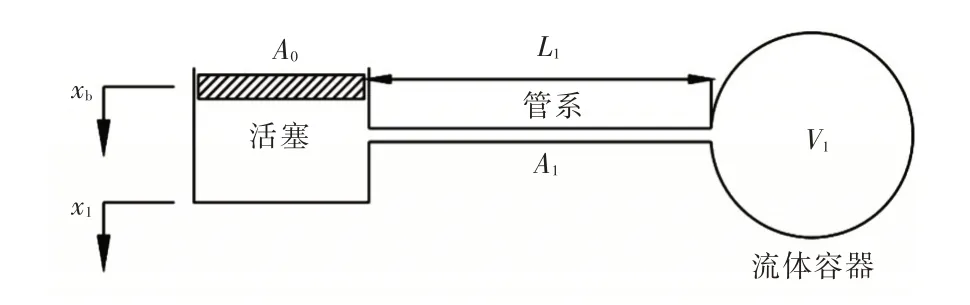
图1 RC 的结构简图Fig.1 Structure diagram of RC

当前，船舶螺旋桨—轴系—船体耦合纵向振动及辐射噪声控制问题备受关注，RC 减振理论模型已逐渐推广运用到船舶振动控制领域。国外学者提出将RC 作为控制船舶轴系纵向振动的减振装置，建立了轴系—船体耦合纵向振动和声辐射响应模型，以求解系统的力传递率和能量传递率，分析等效参数优化和灵敏度，并讨论了参数优化算法及振动控制效果，研究了螺旋桨在不均匀伴流场中旋转产生的纵向脉动力对船体纵向振动和声辐射特性带来的影响［2-5］。近年来，国内学者也陆续开展了基于RC 的船舶轴系纵向振动控制特性分析，针对该装置的参数优化算法、非线性减振特性、振动滤波特性等关键技术问题开展了研究［6-8］。

RC 减振理论模型主要源于Goodwin［1］最早提出的简化经验结论。鉴于RC 内部结构参数与其减振效果密切相关，本文以RC 工程化设计为切入点，拟基于波动理论推导声压在RC 内传播的解析式，构建RC 内部结构参数与其减振机理的物理关系，并对其外接管系通径、长度和外接腔体体积等设计参数的变化对主系统插入损失及宽频带内声压级的影响规律以及灵敏度进行分析，以为RC 实际设计提供理论支持。

1 基于波动理论的RC 振动机理分析

由目前国内外研究现状可知，RC 主要基于动力谐调消振理论来实现对系统特征线谱的抑制。为深入分析RC 对原系统振动特性的影响规律，本文提出基于波动理论研究RC 的振动机理，分析中，主要考虑将理论模型分为2 个部分：活塞纵向行程区域（即原系统设计状态）和外接管系及外接腔体（即RC 设计方案）。首先，分析活塞纵向行程区域中的声压传递特性；然后，求解加装外接管系及外接腔体后系统的振动响应。

1.1 活塞纵向行程区域内声压传递特性分析

图2 所示为活塞纵向行程区域内波动理论分析模型。假设该区域充满流体，且活塞处受到简谐力（F=F0ejωt，其中F0为简谐力倍数值）激励，其他边界均为刚性固定。考虑到RC 以流体为介质，主要利用流体受力产生小变形的特性，在形成相对位移的状态下实现对原系统振动响应的控制。图2 中，L0为活塞在静平衡时受激励力作用纵向可运动的最大范围（行程），La为活塞腔体边界位置，P0为腔体内的流体压力，ox 为活塞纵向行程方向。本文以控制轴系—船体耦合纵向振动为背景，在RC 减振特性研究中重点关注纵向方向。

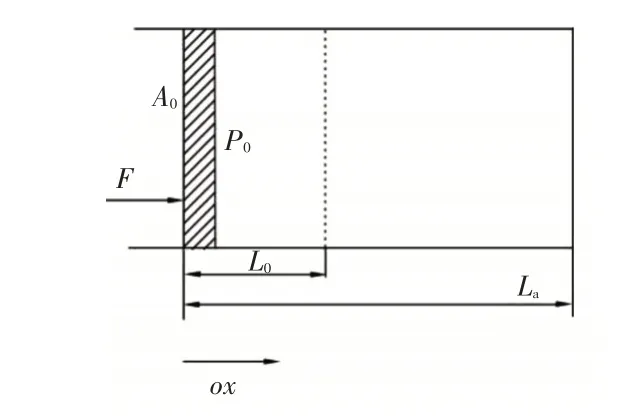
图2 活塞纵向行程区域内波动理论分析模型Fig.2 Analysis model of piston longitudinal motion region based on wave theory

由现有安装方式可知，图2 所示的活塞纵向尺寸相对于外接管系较小，且活塞内流体运动压缩变形小，故不考虑活塞纵向行程区域内的阻尼贡献。

根据连续介质的连续性方程、运动方程和状态方程，求解得到的无阻尼流体介质中小振幅波传播方程为［9］

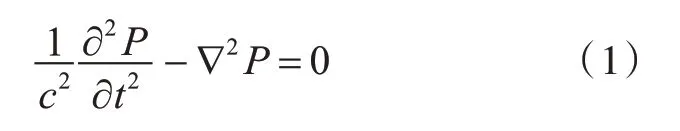
式中：c 为流体声速；P 为流体声压；∇为拉普拉斯算子；t为时间。

流体介质在小振幅声场中的运动方程为

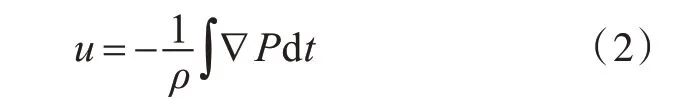
式中：u 为流体介质振动速度；ρ为流体密度。

假设波面振幅均匀声压由P(x，t) 表示，则式（1）可简化为

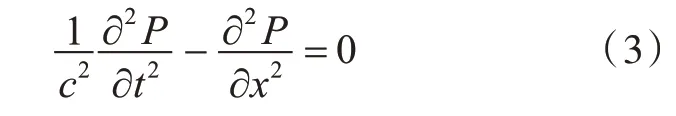
活塞在简谐力激励下的声压通解P(x，t) 一般可表示为

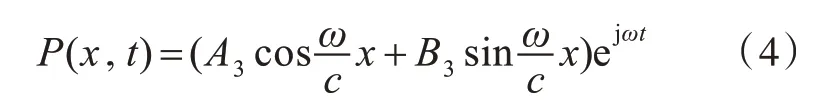
式中：A3，B3分别为待求解的常数；ω为角频率。

图2 所示活塞纵向行程区域内x=L0处为流体受压极限边界，满足u（L0，t）=0，则由式（2）可得

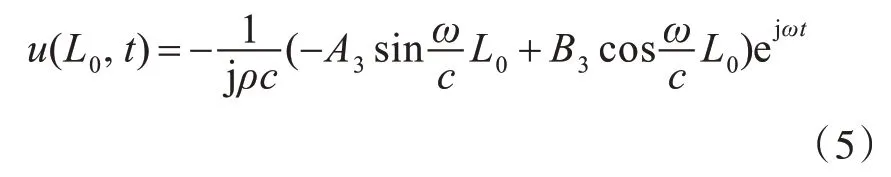
结合边界条件，简化式（5），可得

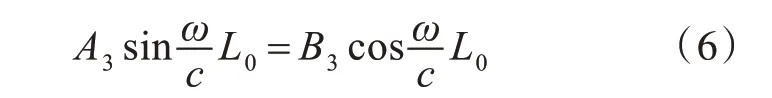
为构建初始状态下压强与激励力之间的关系，针对小幅波传播响应的特点，在不考虑活塞质量的情况下，图2 所示的振动系统可等效为没有质量的等效弹簧系统。故当x=0 时，可知P（0，t）=F0ejωt/A0，将其代入式（4）求解A3，并由式（7）求解P(x，t)。

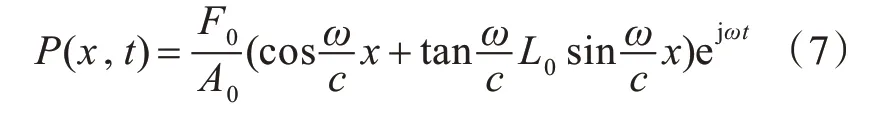
1.2 加装RC 后的系统声压传递特性分析

假设在活塞纵向行程区域x=lh处加装外接管系和外接腔体，将外接管系及外接腔体的集合定义为RC。图3 所示为加装外接管系及外接腔体的波动理论分析模型。图中，d1为外接管系通径，P1为外接腔体内声压。

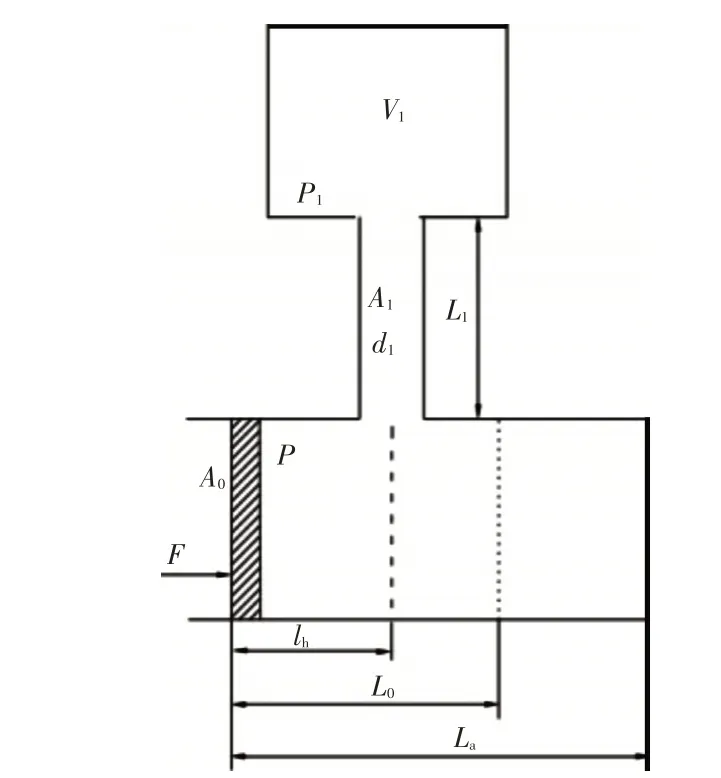
图3 主系统加装RC 后的波动理论分析模型Fig.3 Theoretical model of main system with RC based on wave theory

考虑到RC 与赫姆霍兹共振器的结构形式类似，赫姆霍兹共振器中管系内流体位移与腔内压强变化的对应关系如式（8）所示［10］。

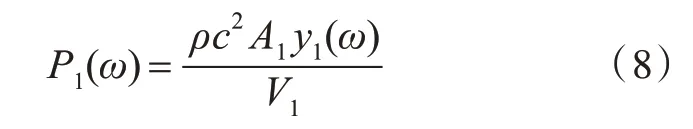
式中，y1(ω) 为管系内流体位移，且假设P1(ω，t)仅为频率与时间的函数。加装外接管系和外接腔体后，根据小振幅波传播的叠加性，在活塞纵向行程lh≤x≤L0范围内的波动响应可等效为活塞处简谐力响应，并叠加了x=lh（lh为RC 加装位置）处因增加RC 而产生的激励源Ph(x′，t)，其中x′的取值范围为［lh，L0］。考虑到叠加波在传播过程中与图2所示边界条件相同，故Ph(x′，t)通解的形式与式（4）一致，可表示为

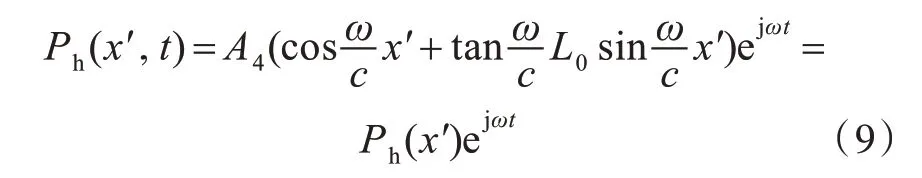
式中，A4为待求解的常数。

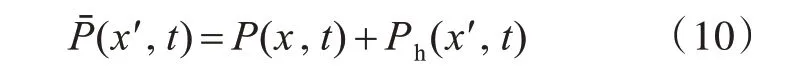
分析外接管系内流体质量（ρA1L1）运动特性，在x′=lh处，计入流体沿程阻尼力的运动方程为

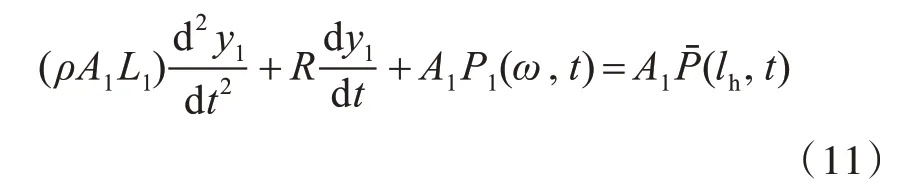
式中，R 为阻尼力系数。

将式（8）代入式（11），可知

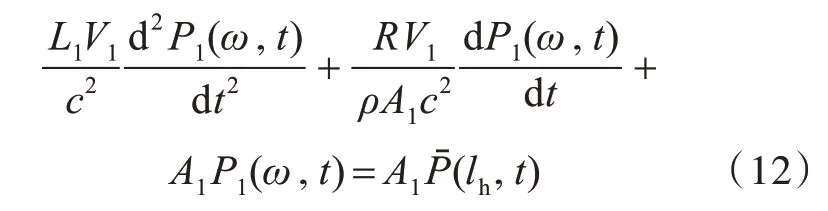
假设流体处于层流状态，则流体经过长度为L1、通径为d1的管系沿程压力损失ΔPf可满足［11］：

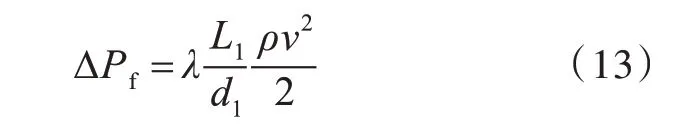
式中：v为流体的特征速度；λ为沿程压力损失因数。

在层流状态下，λ与雷诺系数Re 满足

式中，a 为常数，其取值与流体特性相关。

联立式（13）和式（14）求解R，可得

式中，μ为流体运动粘性系数。引用赫姆霍兹共振器的固有频率ω1与结构尺寸的对应关系［11］：

将式（16）代入式（12）化简，可得

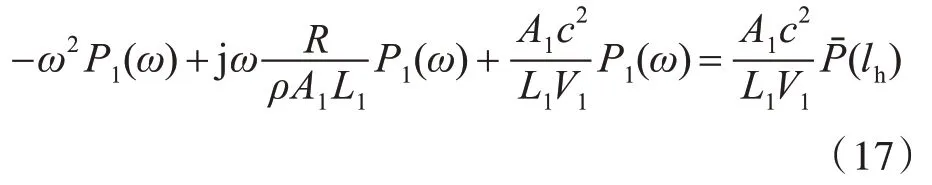
进一步化简式（17），可得P1(ω)与Ph(lh)之间的关系满足

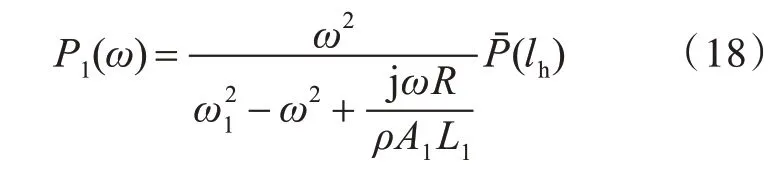
1.3 加装RC 后系统振动特性的解析式

由式（2），可求得活塞在简谐力F 激励下纵向行程区域内x=lh处的流体运动速度u（lh，t）为

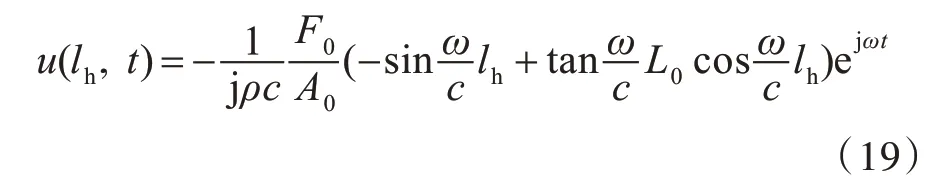
相应地，位移y(lh，t)满足下式：

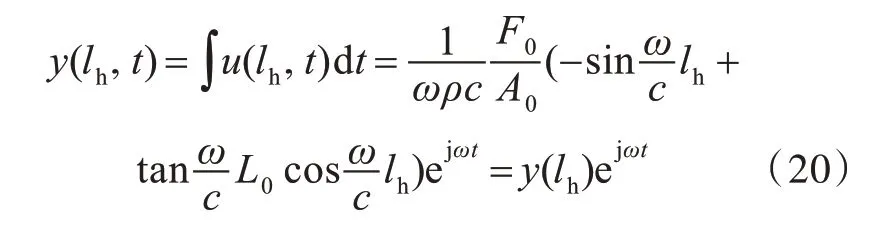
根据x=lh处流体质量守恒，即A0y（lh）=A1y1，结合式（8），可知

联立式（11）、式（18）和式（21），可求解A4，并最终得到(x，t)：

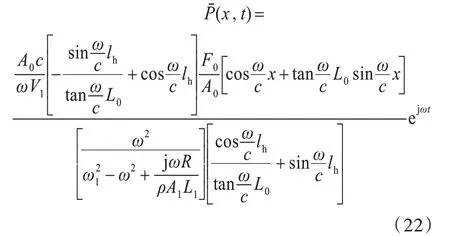
由式（7）和式（22）求解x=L0处的系统插入损失IL，可得

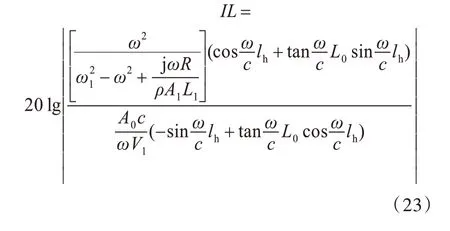
2 RC 结构尺寸对系统减振特性的影响分析

2.1 对系统插入损失的影响分析

根据RC 工程化应用的实际情况，将图2 所示活塞腔体边界位置设为刚性约束，引入系统插入损失作为减振效果的评价指标，并结合图2 和图3研究加装RC 前、后系统的响应差异，分析RC 的减振机理。由式（23）可知，系统插入损失与流体的特征参数、外接管系尺寸、外接腔体尺寸以及活塞尺寸相关。针对初步考虑的RC 减振效果，验证结构尺寸及现有实验条件，开展了不同参数对减振效果的灵敏度分析。表1 给出了相关的初始计算参数。

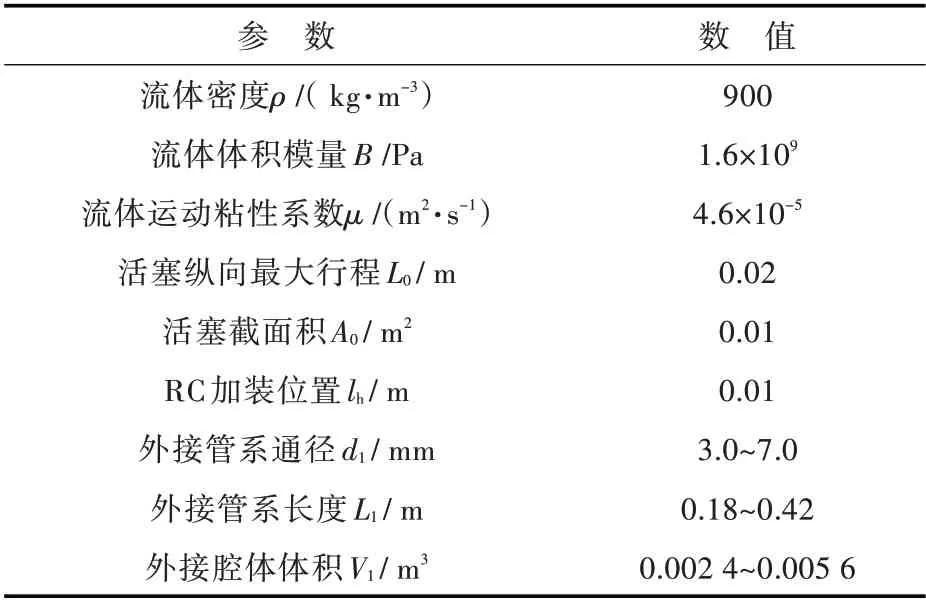
表1 初始计算参数Table 1 Initial calculation parameters

表1 中，流体的密度、体积模量、运动粘性系数与流体的特性相关，活塞纵向最大行程、活塞截面积、RC 加装位置与原系统的设计状态相关。为了合理地对比分析RC 不同结构尺寸对系统减振效果的影响，在后续计算中假设上述基本参数均保持不变。RC 的外接管系通径d1、长度L1以及外接腔体体积V1在设定的取值范围内，以按照从小到大等量增加10%为基准，离散为9 组初始值，并在以上相同变化幅度基准下，对比分析不同结构尺寸对系统减振效果的灵敏度。

2.1.1 外接管系通径

根据定义的外接管系通径d1的取值范围，计算得到系统插入损失和RC 的固有频率f1，如图4所示。

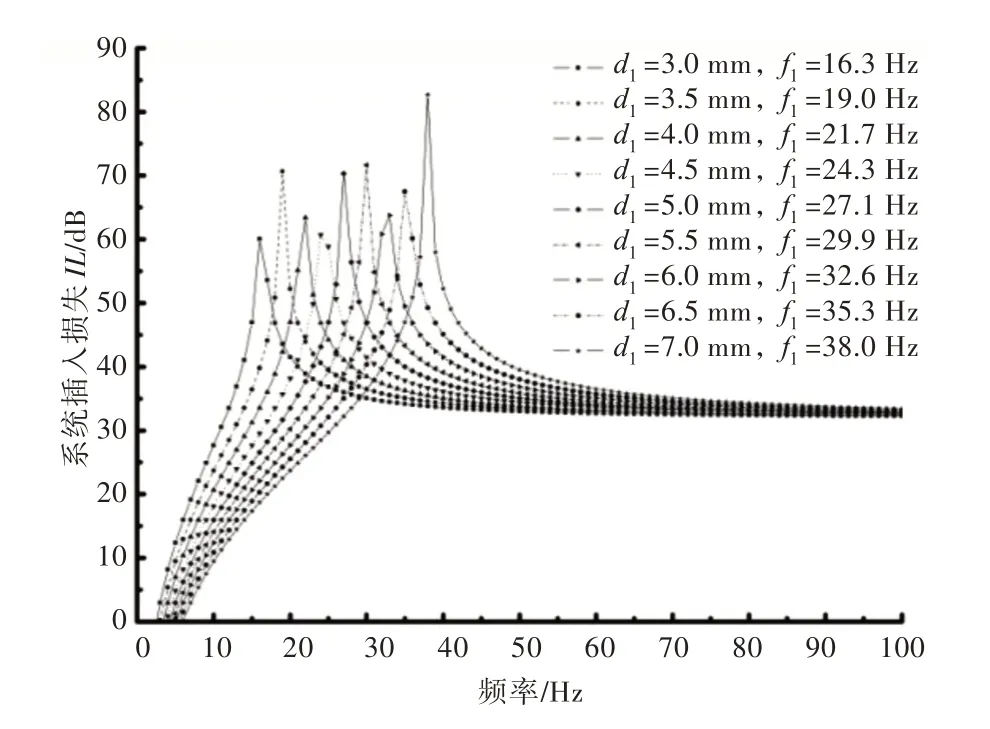
图4 RC 不同外接管系通径对系统插入损失的影响（L1=0.30 m，V1=0.004 m3）Fig.4 Influence of RC pipe diameter variation on insertion loss of system（L1=0.30 m，V1=0.004 m3）

由图4 可知，随着外接管系通径的增加，RC的固有频率增加，插入损失最大幅值对应的频率值与RC 的固有频率相等，这说明RC 对与其固有频率相等的主系统的特征线谱减振效果最好。此结论与RC 的动力谐调消振特征吻合，从固有频率的求解来看，也能相应地验证插入损失推导结果的合理性。针对不同外接管系通径的取值，随着频率的增加，系统插入损失幅值基本为定值，总体呈小幅增大的趋势。

2.1.2 外接管系长度

根据定义的外接管系长度L1的取值范围，计算得到系统插入损失和RC的固有频率f1，如图5所示。

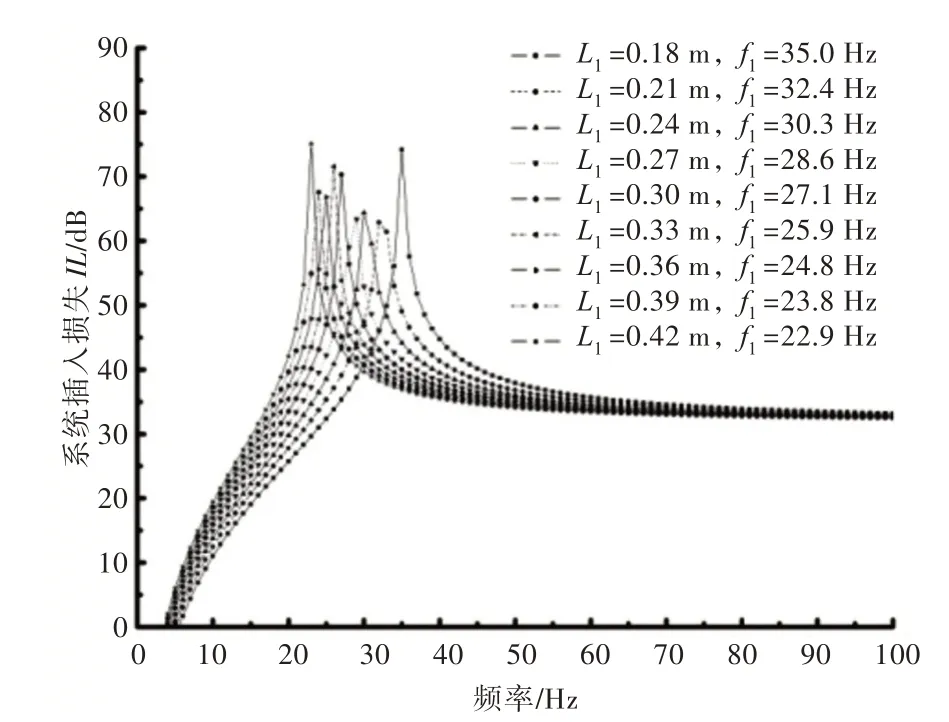
图5 RC 不同外接管系长度对系统插入损失的影响（d1=5.0 mm，V1=0.004 m3）Fig.5 Influence of RC pipe length variation on insertion loss of system（d1=5.0 mm，V1=0.004 m3）

由图5 可知，随着外接管系长度的增加，RC的固有频率减小，而长度变化对不同固有频率处插入损失幅值的影响并非单调增或单调减的关系。随着频率的增加，采用不同的外接管系长度取值计算得到的插入损失幅值基本不变，总体呈小幅减小的趋势。

2.1.3 外接腔体体积

根据定义的外接腔体积V1取值范围，计算得到系统插入损失和RC 的固有频率f1，如图6 所示。

由图6 可知，外接腔体体积变化对系统插入损失幅值的影响与外接管系长度的变化规律接近，系统插入损失随外接腔体体积的增加呈增长的趋势，其递增幅度相比外接管系的影响相对较明显。

2.2 对系统频带内声压级的影响分析

考虑到减振控制中系统频带内声压级变化也是评价减振装置减振效果的重要指标之一，为从系统总体角度研究RC 的减振特性，选取0～100 Hz频率分析RC 对系统频带内声压级的控制效果。根据表1 所列相关参数的取值，结合式（7）和式（22），可求解得到加装RC 前、后的声压级减少量。图7 所示为外接管系通径、长度及外接腔体体积在离散取值下计算得到的系统频带内声压级减少量。

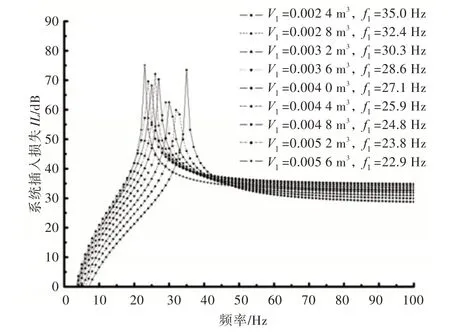
图6 RC 外接腔体体积对系统插入损失的影响（d1=5.0 mm，L1=0.30 m）Fig.6 Influence of RC cavity volume variation on insertion loss of system（d1=5.0 mm，L1=0.30 m）

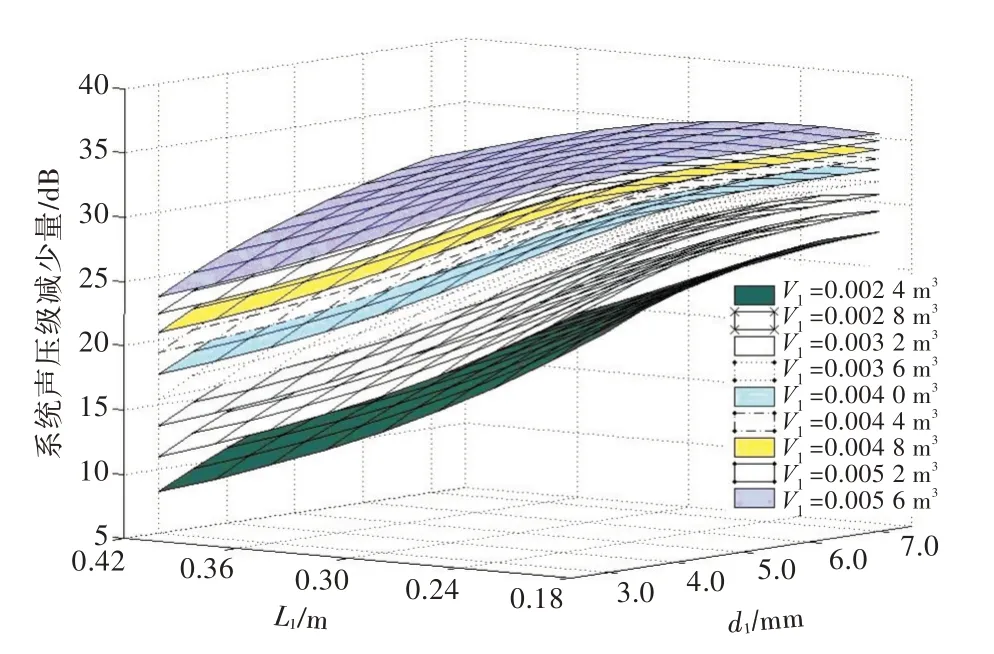
图7 在0～100 Hz频带内RC结构参数对声压级减小量的影响Fig.7 Influence of RC structural size variation on sound pressure level reduction within 0～100 Hz frequency band

由图7 可知：外接腔体体积V1从0.002 4 m3增至0.005 6 m3，在0～100 Hz 分析频带内，系统声压级减少量提高了约15 dB；外接管系通径的增加将提高RC 对系统频带内声压的减振效果，但增幅随着外接腔体体积的增大而逐步减缓；外接管系长度的增加总体上能够实现对系统频带内声压的减振，但尺寸越大，对系统的减振效果呈逐步下降的趋势。

3 RC 结构尺寸变化对系统减振效果的灵敏度分析

根据以上RC 结构尺寸变化对系统减振效果的影响规律可知，在RC 的固有频率处，系统插入损失幅值最大；从0～100 Hz 频带内的声压级减少量来看，不同结构尺寸对系统的减振效果影响有所不同。为此，针对各类结构尺寸变化的幅度同步细化开展了系统减振效果的灵敏度分析，结果分别如表2～表4 所示。由各表可知外接管系的通径、长度及外接腔体体积取值与RC 固有频率处插入损失最大值（ILmax）、频带内声压级减少量的对应关系。

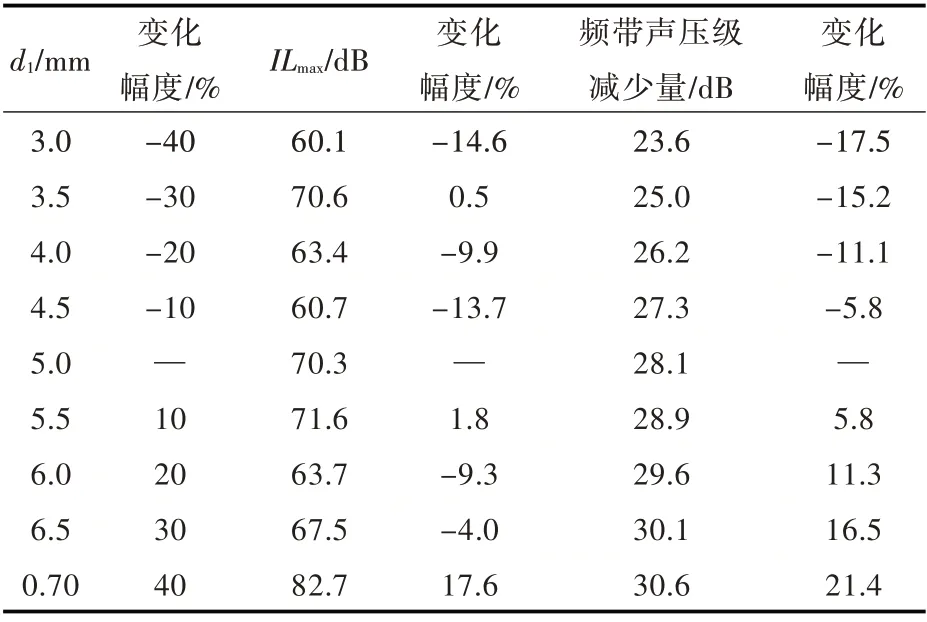
表2 外接管系通径与系统插入损失最大值、频带内声压级减少量的对应关系（L1=0.30 m，V1=0.004 m3）Table 2 Interrelation between pipe diameter variations and insertion loss maximum，sound pressure level reduction（L1=0.30 m，V1=0.004 m3）

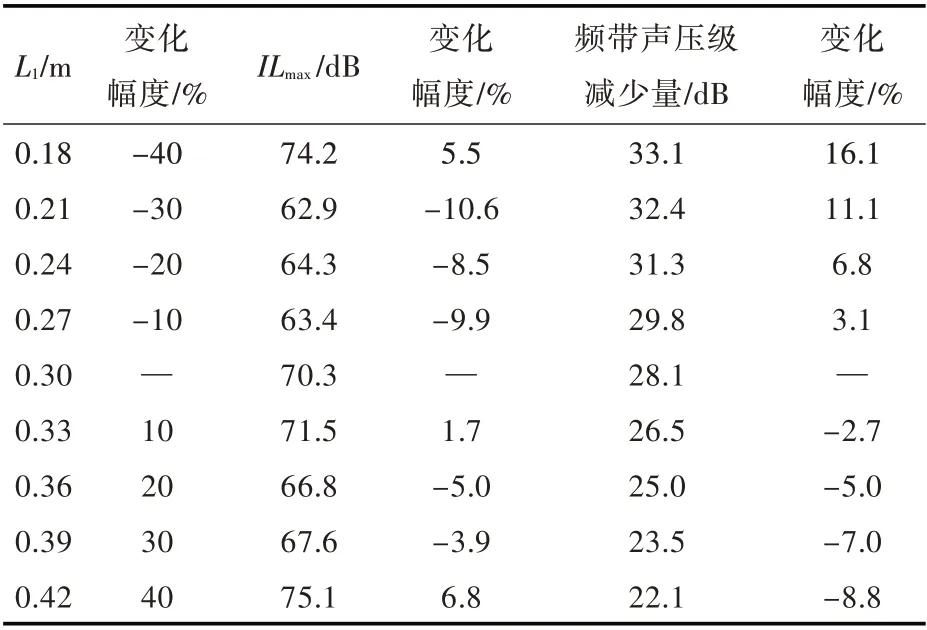
表3 外接管系长度与系统插入损失最大值、频带内声压级减小量的对应关系（d1=5.0 mm，V1=0.004 m3）Table 3 Interrelation between pipe length variation and maximum insertion loss，sound pressure level reduction（d1=5.0 mm，V1=0.004 m3）

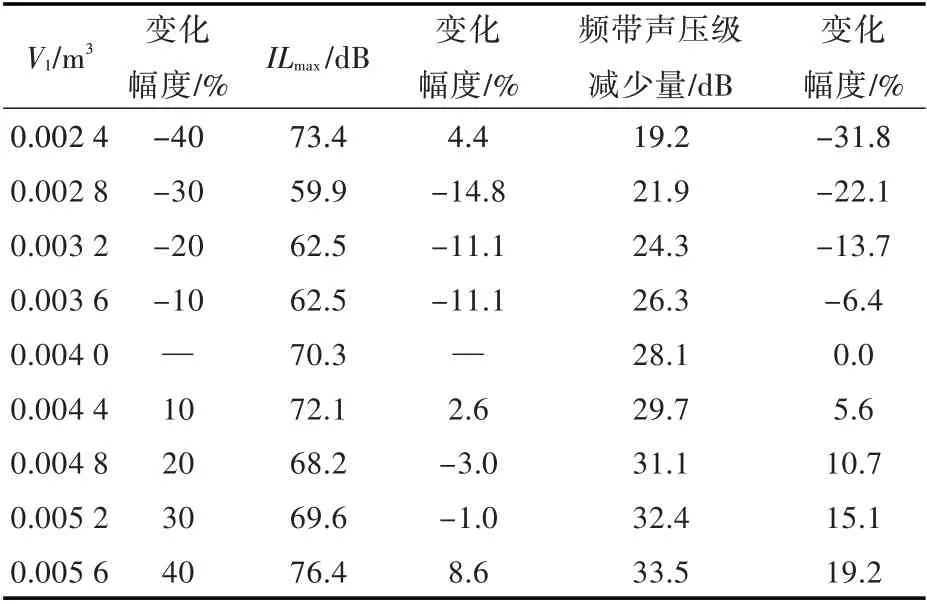
表4 外接腔体体积与系统插入损失最大值、频带内声压级减小量的对应关系（d1=5.0 mm，L1=0.30 m）Table 4 Interrelation between cavity volume variation and maximum insertion loss，sound pressure level reduction（d1=5.0 mm，L1=0.30 m）

图8 和图9 所示为RC 各结构参数变化幅度对系统振动控制效果的灵敏度分析结果。

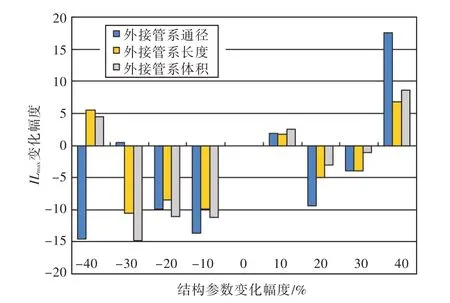
图8 RC结构参数变化幅度对系统插入损失最大值的灵敏度Fig.8 Sensitivity of RC structural parameter variation to maximum insertion loss

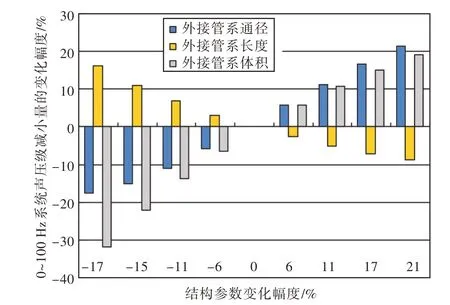
图9 RC 结构参数变化幅度对系统声压级减少量的灵敏度Fig.9 Sensitivity of RC structural parameter variation to sound pressure level reduction

由图8 可知，以RC 外接管系通径d1=5.0 mm、外接管系长度L1=0.30 m、外接腔体体积V1=0.004 m3为基准，针对各类参数在±10%，±20%，±30%，±40%变化条件下，分析系统插入损失最大值的变化幅度改变情况。总体上，外接管系通径对系统插入损失最大值的影响较为敏感，外接管系长度的影响次之，外接腔体体积的影响相对较小。因此，在针对特征线谱消振需求开展RC 结构参数设计时，建议重点关注外接管系尺寸的选择。

由图9 可知，外接腔体体积对系统频带内声压级减少量的影响较为敏感，外接管系通径的影响次之，而外接管系长度的影响则相对较小。因此，针对频带内减振控制需求开展RC 结构参数设计时，建议重点关注外接腔体尺寸的选择。

4 结 论

本文基于波动理论开展了RC 减振特性研究，求解了加装RC 后声压传播的解析式，并选择不同的RC 外接管系通径、长度及外接腔体体积，开展了各结构尺寸变化对系统插入损失幅值和频带内声压级的影响特性分析及灵敏度分析，得到如下主要结论：

1）RC 在其固有频率处能够对主系统共振峰实现有效控制，减振效果明显；外接管系通径、长度和外接腔体体积的变化对固有频率处插入损失最大值的影响不具有单调增或单调减的规律；随着频率的增加，插入损失随着外接管系通径、外接腔体体积的增加呈小幅增长的趋势，而随外接管系长度的增加则呈小幅减小的趋势；同时，由各结构尺寸的变化对插入损失最大值的灵敏度分析可知，针对特征线谱消振需求开展RC 结构参数设计时需重点关注外接管系尺寸的选择。

2）以实现在0～100 Hz 频带内减小系统声压级为目的，分析RC 结构尺寸变化对减振效果的影响可知，外接腔体体积和外接管系通径的增加可提高频带内的减振效果，外接管系长度的增加对系统频带内的减振效果呈逐渐下降的趋势；同时，由各结构尺寸变化对频带内声压级减少量的灵敏度分析可知，针对频带内减振控制需求开展RC 结构参数设计时需重点关注外接腔体尺寸的选择。