罗经方位对准的收敛时间分析

何东旭，葛磊，张鑫，臧新乐

1 哈尔滨工程大学自动化学院，黑龙江哈尔滨150001

2 北京计算机技术及应用研究所，北京100854

0 引 言

罗经对准是惯性导航系统常用的一种初始对准方法，该方法基于“罗经效应”原理［1］，应用经典控制理论，在频域上设计罗经对准回路，罗经对准具有设计参数少、计算量小、易于实现等优点，因此，该方法一直是初始对准研究方向的热点。

罗经对准分为水平对准和方位对准2 种，一般来讲，水平对准速度快、精度高，难度较小，而方位对准则是整个对准过程的关键和难点。李瑶等［2］研究了摇摆状态下的捷联惯导系统罗经法自对准技术，设计优化了水平和方位对准参数，该方法在不同海情、不同初始姿态误差和全方位条件下具有良好的对准结果。徐博等［3］研究了航行转台下的罗经回路初始对准，并基于器件误差情况等效分析了航行状态下的对准误差；张娟秀等［4］分析了随机噪声对罗经方位对准的影响，并创新性地提出了时域下的分析方法；Gao 等［5］研究了基于姿态逆向解算的罗经对准方法，并提出陀螺输出的周期震荡误差会使罗经方位对准产生额外的震荡误差，且方位误差会随切换次数的增加而放大；He 等［6］提出了基于最优模型的时变参数罗经对准算法，并利用遗传算法对大方位失准角条件下的罗经对准参数进行了优化。

尽管研究罗经对准的文献较多，但是针对罗经对准收敛时间的研究较少。而对于罗经对准来说，收敛时间也是一项较为重要的指标，因为在固定的初始对准时间内，既希望系统抗干扰能力强，能将环境的随机干扰降低到最小，又要使系统能在初始对准时间内收敛，而这二者往往相互矛盾［6］。严恭敏［7］设计了四阶罗经方位对准控制系统，指出罗经方位对准收敛时间与设置的二阶阻尼震荡周期有关，但其只对经典的二阶系统进行了分析，并以此类比了四阶罗经方位对准控制系统，但是采用二阶系统的分析方法类比分析四阶系统显然不够严谨。高钟毓［8］设计了三阶罗经对准系统，指出在选择相应的参数时，该系统会在30～50 min收敛，但是并没有给出具体的分析方法。

基于以上原因，本文将基于通常设置的四阶罗经方位对准系统，分析东向陀螺漂移和初始方位误差对罗经方位对准收敛时间的影响。提出将方位误差的频域响应转化成时域响应函数，并在时域上分析收敛时间，巧妙地将方位误差从频域转化到时域进行研究，并得出相关结论，为罗经方位对准设置相关参数以及控制收敛时间提供理论参考。

1 罗经方位对准原理

罗经方位对准是一种利用“罗经效应”原理、基于经典控制理论的自对准方法，罗经初始对准分为水平对准和方位对准2 个阶段，其中方位对准是在水平对准的基础上进行的，这里只简单介绍罗经方位对准的原理。

罗经方位对准原理如图1 所示。图中：R为当地子午圈半径；s 为拉普拉斯算子；εU为天向陀螺漂移，一般来说，对初始对准精度的影响较小；ωie为地球自转角速度；L为当地地理纬度；g为重力加速度；ΔN为北向加速度计偏置；εE为东向陀螺漂移；δVN为北向速度误差；φx为东向失准角，φz为方位失准角；K1，K2为北向水平回路的设计参数；K(s) 为罗经回路控制环节，K(s)=K3[ωiecosL(s+K4)]，其输入信号为δVN，输出信号为K(s)δVN，以代替天向控制指令角速度。在罗经方位对准过程中，从φz开始，经罗经效应的各个环节，到输出δVN，再经过方位控制环节K(s)，调整输出φz。

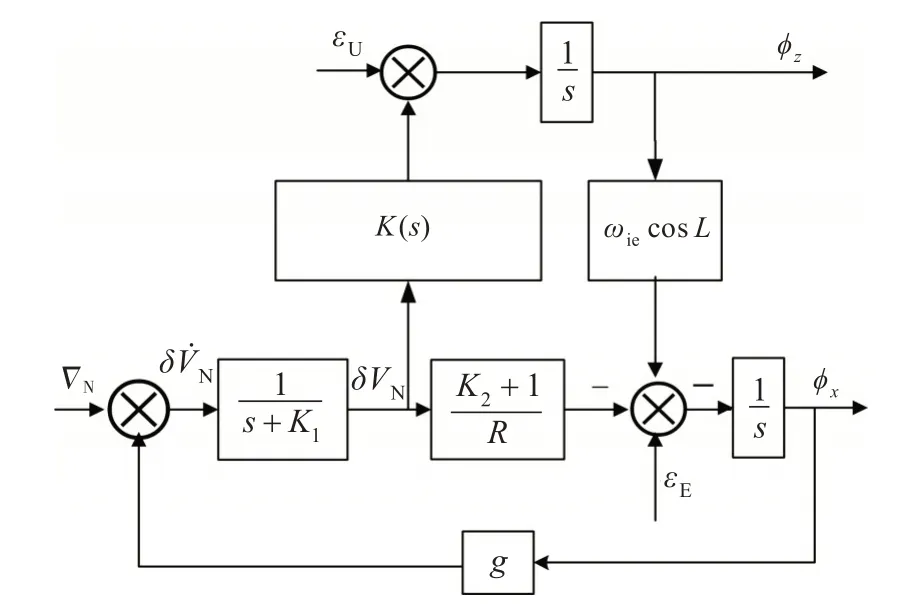
图1 罗经方位对准原理图Fig.1 Schematic diagram of compass azimuth alignment

根据上面罗经方位对准原理图，可知该四阶系统的响应为

式中：φx(0)为初始东向失准角，当罗经对准经水平调平后，这一项的值非常小，对罗经方位对准无影响；φz(0)为初始方位角误差，该误差会影响罗经方位对准的收敛特性，是需要重点研究的对象；εE会影响方位对准精度；Δ(s)为罗经方位对准系统的特征方程，且

一般来说，较为成熟的参数设置方法是将1 个四阶系统变成2 个相同的二阶系统的串联形式，且该系统的特征根有如下形式［2］：

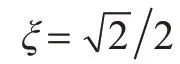
因此，在罗经方位对准中，只需设定好Td的值，其它参数也就相应确定［10］。实际上，参数Td的设置与初始对准时间、初始方位误差、惯性器件的随机漂移以及载体晃动干扰情况都有关，也是罗经方位对准中需重点研究的方向，不过在本文中，不讨论参数Td的设置问题。

从φz的频域响应函数可知，φz的输出受5 个参数的影响，但由相关文献可知，ΔN，φx(0)和εU对罗经方位对准的影响也较小，且其数量级都很小，所以这里不考虑这3 个参数对收敛速度的影响，本文重点分析东向陀螺漂移εE和初始方位角误差φz(0)对罗经方位对准收敛时间的影响。

2 罗经方位对准收敛时间分析

2.1 罗经方位对准收敛判定

一般在自动控制理论中，通常被控制参数进入到某个误差带中，则认为系统进入稳态过程，即系统收敛。并且在自动控制理论中，一般取误差带为稳态值的2%或5%。但在研究罗经方位对准时不宜这样选取，因为初始方位误差对罗经方位对准影响的稳态值为0，无法以稳态值的百分比取误差带；另外，在初始对准时，通常需要根据惯性器件精度及对方位角精度的要求，综合考虑方位收敛的判据，因此，本文以方位角进入到以角度为单位的误差带作为罗经方位对准收敛的判据。

在本文中，限定陀螺零偏稳定性在0.05（°）/h以内，根据初始对准误差公式可知，在北纬53 °以内，其初始对准误差在0.35 °以内，再综合考虑随机误差对初始对准的影响，本文取0.01 °的误差带，这对于中等惯性器件精度的初始对准来说，可以认为已经收敛。当然，在实际应用中，可根据实际应用环境、惯性器件精度及对准精度的要求，对收敛判据进行调整。如果陀螺零偏稳定性在0.001（°）/h 的量级，则可将误差带提高至0.005 °，如果陀螺零偏稳定性在0.1（°）/h 量级，则可将误差带放宽至0.02°或0.03°。

2.2 陀螺常值漂移对收敛时间的影响

由第1 节可知，与东向陀螺漂移有关的系统响应项为

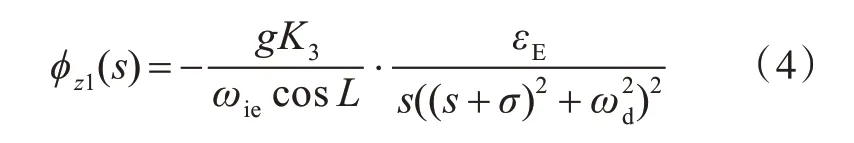
为了考察该响应的时间特性，将其频域响应转化成时域响应函数Td，对φz1(s)求取拉普拉斯反变换，则有

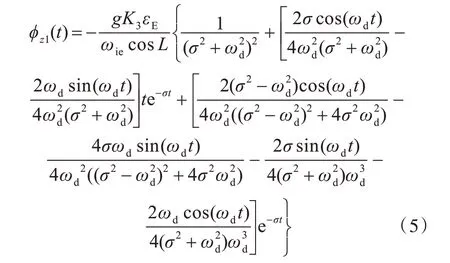
按照第1 节相关参数取值，有σ=ωd=2πTd，gK3=4σ4，因ωd与σ只是在数值上相等，其物理含义并不相同，因此，涉及到正余弦运算的ωd不用σ替换。式（5）可简化为

由上式可以看出，φz1(t)收敛于-εEωiecosL，这与相关文献中东向陀螺漂移对初始对准的影响的相关公式吻合［11］，而这里要考虑的是φz1(t)何时收敛。

由于在本文中限定陀螺零偏稳定性小于0.05（°）/h，则陀螺常值漂移一般小于0.05（°）/h，再取纬度为53°，则此时有

考虑上式中的4 个衰减震荡误差项，有

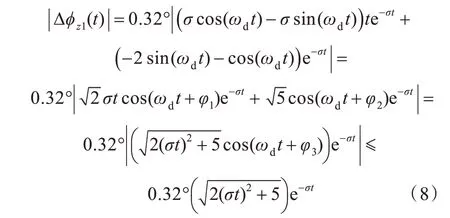
式中，φ1～φ3为相位角。

取0.01°误差带判定罗经方位对准收敛，则有

则 可 解 得σt=5.57 ，从 而 有t=5.57σ=5.57Td2π ≈0.9Td，即经过约0.9 个阻尼震荡周期，罗经方位对准收敛到0.01°的误差带。

因此，可以得出结论：东向陀螺漂移对罗经方位对准造成的影响至多可在0.9 个阻尼震荡周期内收敛。本文的分析过于保守，随着陀螺精度的提高，其常值漂移会减小，则其收敛时间将会更短。表1 列出几个典型陀螺常值漂移条件下的收敛时间。

表1 不同陀螺常值漂移的收敛时间Table 1 Convergence time of different gyros constant drift

从表1 可以看出，罗经方位对准的收敛时间与设置的二阶阻尼震荡周期和陀螺常值漂移有关，当陀螺常值漂移确定时，收敛时间与二阶阻尼震荡周期存在固定的比例关系；而当二阶阻尼震荡周期确定时，陀螺常值漂移越大，则收敛时间越长，陀螺常值漂移越小，则收敛时间越短。

还有一点要说明，在进行收敛时间的理论计算时，由于采用了不等式放大，故实际收敛时间往往会小于所计算的理论时间，因此，此处的收敛时间较为保守，是系统稳定所需的最长时间。

2.3 初始方位误差对收敛时间的影响

由第1 节可知，与初始方位误差有关的系统响应项为

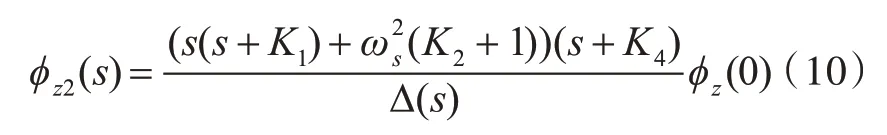
按照第1 节的相关参数取值，则有

对其求拉普拉斯反变换，得到时域响应函数：

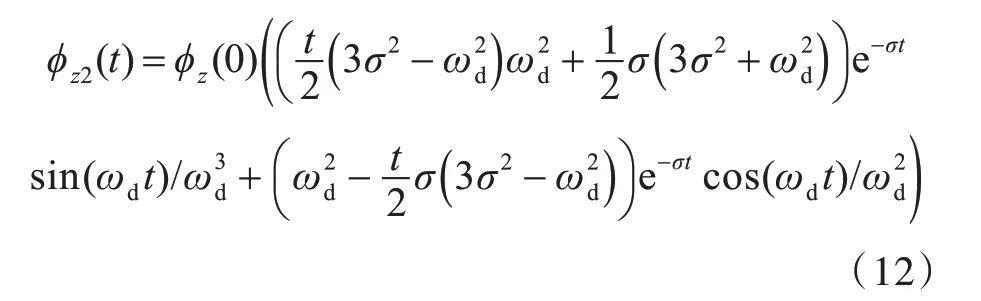
由于在参数设置中有ωd=σ，故有

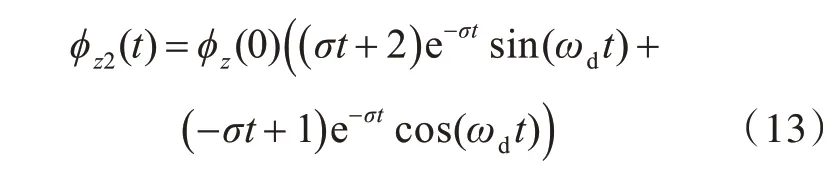
从上式可以看出，φz2(t) 最终收敛于0，而本文研究的目标是其何时收敛。

由于

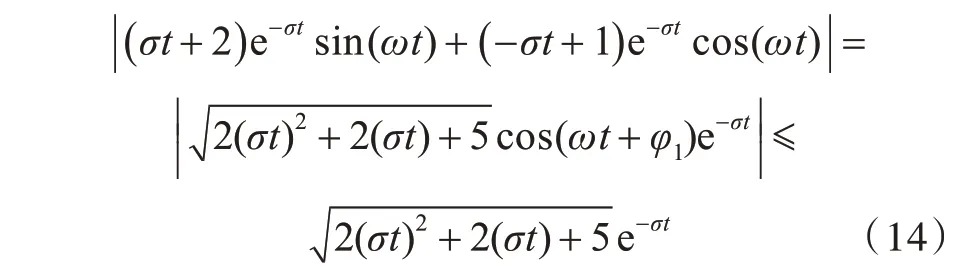
因此有

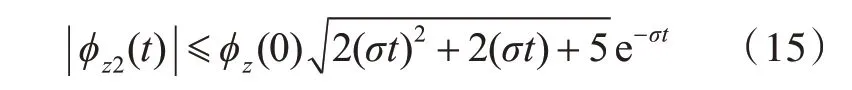
以0.01°的误差带为判定初始对准收敛的判据，则有

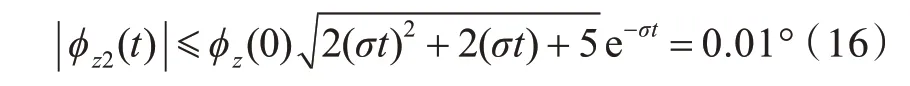
根据上式可知，φz2(t)的大小与初始方位误差φz(0)成比例关系，因此其收敛时间与初始方位角误差的大小有关。并且从上式还可以简单看出，φz(0)越大，收敛时间越长。

一般来说，在进行罗经对准前，需要进行粗对准［12］，以保证罗经方位对准误差模型的线性特性。当初始方位角误差在5 °以内时，惯导误差模型具有较好的线性特性，利用罗经方位对准进行初始对准效果较好；当初始方位角误差大于5 °时，惯导误差模型的线性度逐渐变差，罗经方位对准的性能就会变差。因此，在实际应用中，粗对准的误差一般要控制在5 °以内，而本节也只研究初始方位误差在5 °以内的罗经方位对准收敛时间。并且，由于水面舰艇上的罗经装备在实际使用中初始方位误差不会太大，一般会在1°以内，因此本文重点列出初始方位误差在1°以内时罗经方位对准的收敛时间。根据式（16），列出了在一些典型初始误差值条件下罗经方位对准的收敛时间，如表2所示。

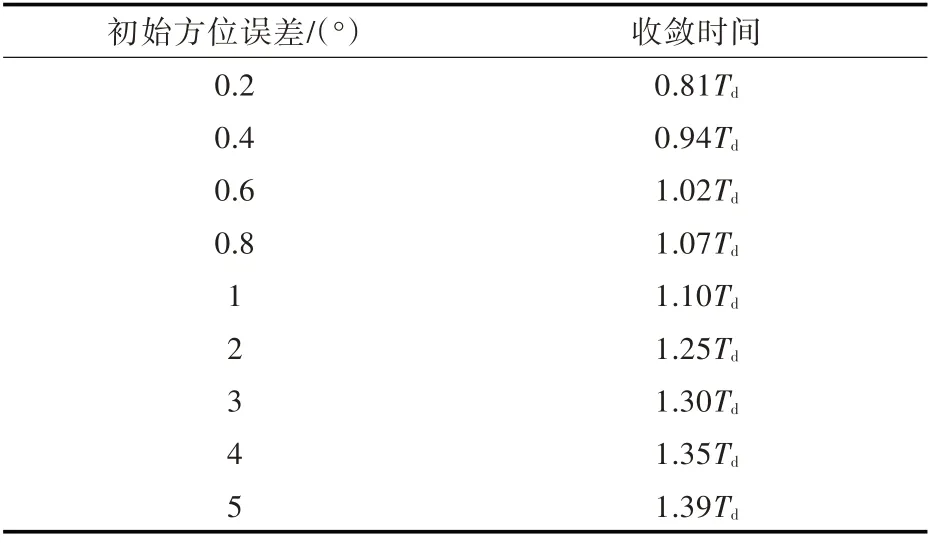
表2 不同初始方位误差的收敛时间Table 2 Convergence time of different initial azimuth misalignment

从表2 可以看出，罗经方位对准的收敛时间与设置的二阶阻尼震荡周期和初始方位误差有关，当初始方位误差确定时，收敛时间与二阶阻尼震荡周期存在固定的比例关系；而当二阶阻尼震荡周期确定时，初始方位误差越大，则罗经方位对准的收敛时间越长，初始方位误差越小，则罗经方位对准收敛时间越短。

与2.2 节同理，表2 所列的收敛时间也较为保守，一般情况下，实际收敛时间要小于理论计算出的时间。

2.4 两种误差共存时对收敛时间的影响

在惯导实际的初始对准中，陀螺常值漂移和初始方位误差是同时存在的，因此，分析2 种误差同时存在，对收敛时间的影响很有必要，对实际应用中罗经方位对准的参数设置具有重要的理论指导意义。

陀螺常值漂移和初始方位误差相互独立，则根据自动控制理论可知，二者经罗经方位对准传递函数得到的响应可以线性叠加，因此当2 种误差同时存在时，罗经方位对准误差的响应函数为

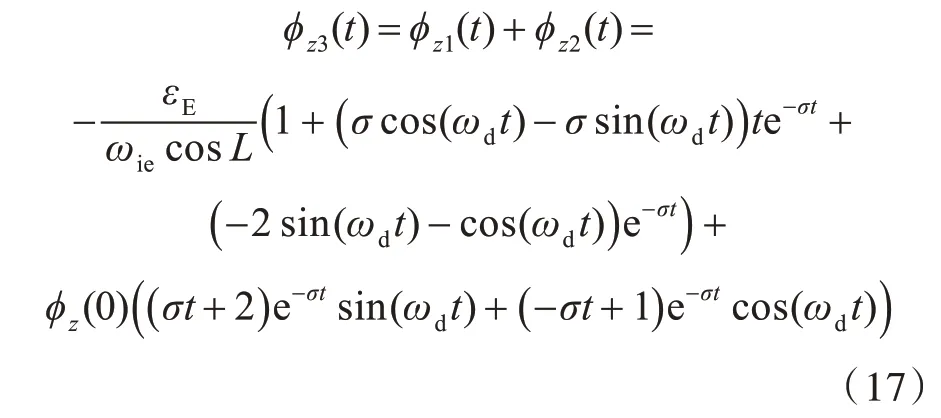
从上式可以看出，当2 项误差同时存在时，φz3(t)收敛于-εEωiecosL，误差衰减震荡项为

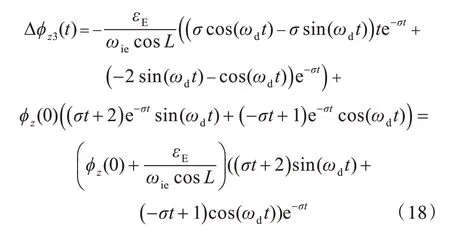
因此有

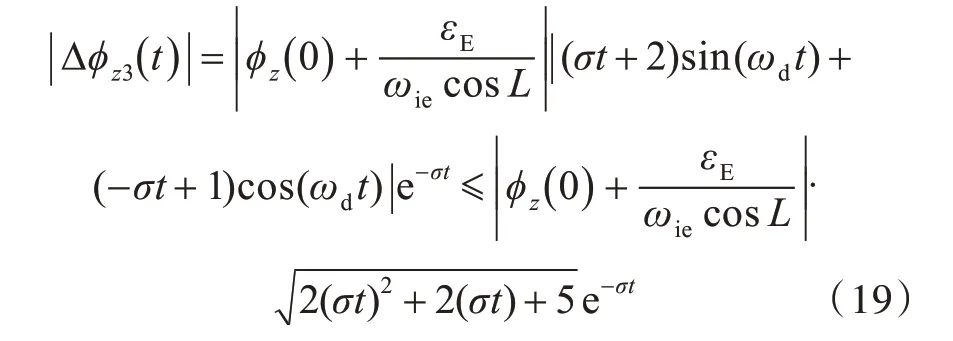
以0.01 °的误差带为判定初始对准收敛的判据，则有

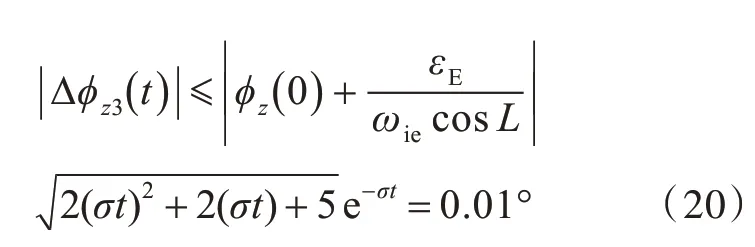
表3 列出了一些典型初始方位误差和陀螺常值漂移下的收敛时间。

表3 典型初始方位误差和陀螺常值漂移下的收敛时间Table 3 Typical convergence time of different initial azimuth misalignment and gyro constant drift

对比表2 和表3 可以看出，相对于初始方位误差，陀螺常值漂移对收敛时间影响不大，主要影响收敛时间的因素是初始方位误差。

因此，可以得出结论：当陀螺常值漂移和初始方位误差同时存在时，影响罗经方位对准的主要因素为初始方位误差；当陀螺常值漂移在0.05（°）/h以内，初始方位误差在5 °以内时，罗经方位对准会在至多1.41Td时间内收敛，初始方位误差越小，收敛时间也会越短。

3 仿真验证

在本节仿真中，首先分别验证陀螺常值漂移和初始方位误差对罗经方位对准收敛时间的影响，再验证二者共同存在时对罗经方位对准收敛时间的影响，主要验证这3 种条件下罗经方位对准收敛时间是否与理论分析相吻合。

3.1 陀螺常值漂移对收敛时间影响仿真

假设参考坐标系为东北天坐标系，当地地理纬度为53 °，惯导只有X 轴陀螺具有0.05（°）/h 的常值漂移，惯导的姿态为0 °，0 °，0 °，初始姿态误差皆为0°，设置Td分别等于200，300，400 和500 s，仿真时间为600 s，得到初始对准误差收敛曲线如图2 所示。

图2 陀螺常值漂移0.05（°）/h 时不同Td下的误差收敛曲线Fig.2 Convergence curves in different Td with 0.05（°）/h gyros constant drift

由初始对准相关理论可知，此时初始对准误差稳定值为-0.316 5°。因此，结合上图和本文0.01°误差带的定义可知，初始对准误差曲线在最后一次穿过-0.326 5 °时，即可认为罗经方位对准收敛，此时，对于不同的Td，收敛时间分别如表4所示。

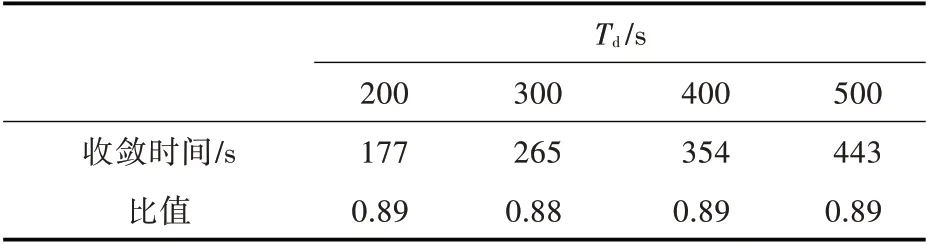
表4 陀螺漂移0.05（°）/h 时不同Td的收敛时间Table 4 Convergence time of different Td with 0.05（°）/h gyros constant drift

从表4 可以看出，对于不同的Td，虽然收敛时间不同，但是收敛时间与Td的比值与理论分析结果吻合较好，验证了所提出分析方法的有效性。

限于篇幅，这里不再画出其它陀螺漂移时的收敛曲线，只通过表5 列出陀螺漂移取0.01，0.02，0.03 和0.04（°）/h，Td取200，300，400 和500 s 时的收敛时间及收敛时间与Td的比值。

表5 不同Td和陀螺常值漂移下的收敛时间Table 5 Convergence time of different Td and different gyros constant drift

从表5 可以看出，当陀螺漂移在0.02（°）/h 以上时，与理论计算结果吻合较好，而在0.02 和0.01（°）/h 时，实际收敛时间要小于理论收敛时间，其原因是在理论推导过程中采用了不等式的放大，使得理论计算的收敛时间过于保守，但从总体来说，本文的分析方法是有效的。

3.2 初始方位误差对收敛时间影响仿真

假设惯性器件无误差，初始方位误差为5 °，设置Td分 别 为200，300 ，400 和500 s，仿 真 时间 为1 000 s，姿态为0 °，0 °，0 °，仿真结果如图3和表6 所示。

图3 初始方位误差5°时不同Td值下的收敛曲线Fig.3 Convergence curves in different Td with 5°initial azimuth misalignment

表6 初始方位误差5°时不同Td的收敛时间Table 6 Convergence time of different Td with 5°initial azimuth misalignment

从表6 可以看出，对于不同的Td，虽然收敛时间不同，但是收敛时间和Td的比值与理论分析结果吻合较好，验证了所提出分析方法的有效性。

限于篇幅，本文不再画出其它陀螺漂移时的收敛曲线，只通过表7 列出一些典型初始方位误差条件下的收敛时间。特别考虑了水面舰艇上罗经装备初始方位误差一般不超过1°的实际使用情况，也重点列出了初始方位误差在1°以内时对罗经方位对准收敛时间的影响。因此表7 列出了初始方位误差为4 °，3 °，2 °，1 °，0.8°，0.6°，0.4°和0.2°，Td取200，300 ，400 和500 s 时的收敛时间及其与Td的比值。

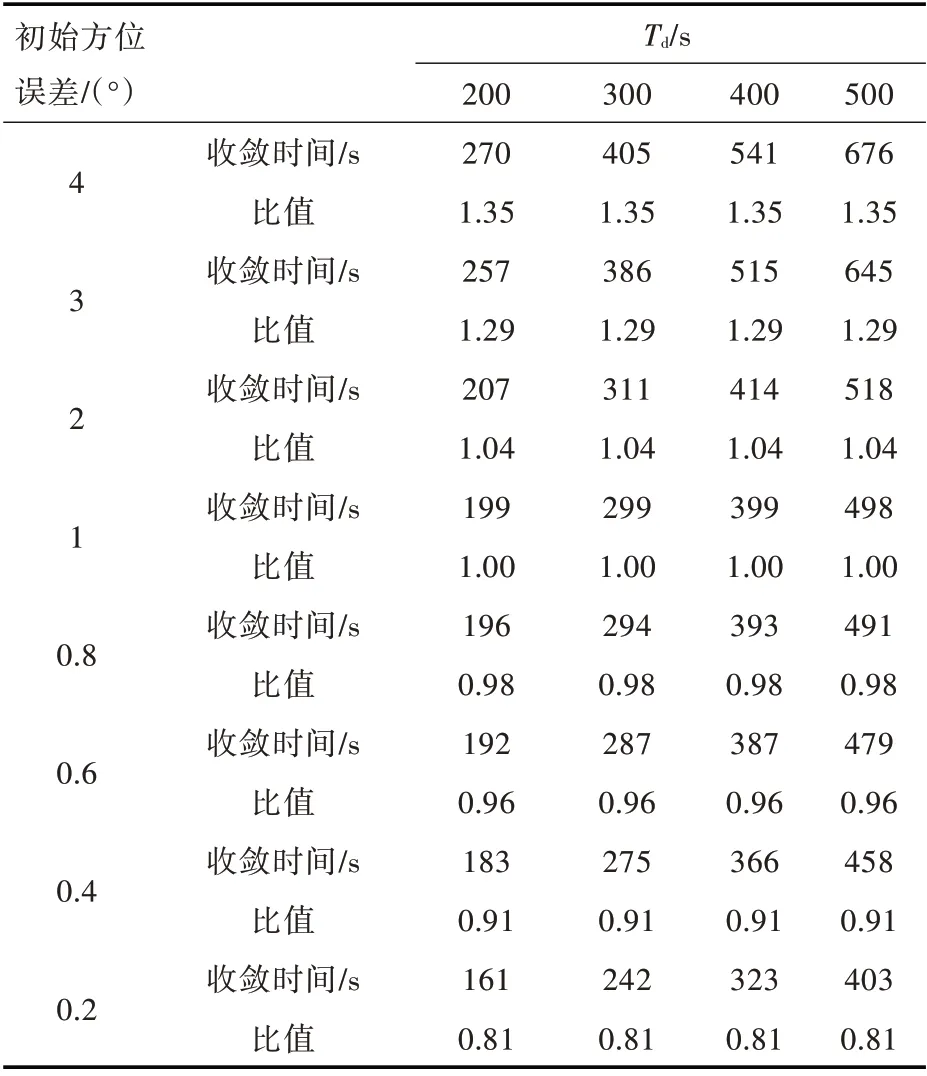
表7 不同Td和初始方位误差下的收敛时间Table 7 Convergence time of different Td and different initial azimuth misalignment

从表中可以看出，当初始方位误差大于2 °时与理论计算结果较为吻合，而当初始方位误差小于2°时，实际收敛时间要小于理论计算时间。这一现象是由于在理论分析中采用了不等式的放大而造成，但总体来说，本文所提出的分析方法有效。

3.3 两种误差共存时对收敛时间影响仿真

假设惯性器件无误差，初始方位误差为5 °，陀螺常值漂移为0.05（°）/h，设置Td分别为200 ，300，400 和500 s，仿真时间为1 000 s，姿态为0 °，0°，0°，仿真结果如图4 和表8 所示。

限于篇幅，这里不再画出其它条件下的收敛曲线，只通过表9 列出初始方位误差取4 °，3 °，2 °，1 °和0.5 °，陀螺常值漂移取0.05（°）/h，Td取200，300，400 和500 s 时的收敛时间及其与Td的比值，以验证理论分析的有效性。

图4 不同Td值下的收敛曲线Fig.4 Convergence curves in different Td

表8 陀螺漂移0.05（°）/h 和初始方位误差5°时不同Td的收敛时间Table 8 Convergence time of different Td with 0.05（°）/h gyro drift and 5°initial azimuth misalignment

表9 陀螺漂移0.05（°）/h 时不同Td和初始方位误差下的收敛时间Table 9 Convergence time of different Td and different initial azimuth misalignment with 0.05（°）/h gyro drift

对比表9 可以看出，当陀螺漂移设置到较大值0.05（°）/h 时，不同初始方位误差条件下的收敛时间差别不大，且都与Td时间相关，成比例关系，进而验证了本文所提分析方法的正确性。

4 结 论

罗经方位对准的精确性和快速性往往互相矛盾，在固定的初始对准时间内，既希望尽可能多地滤掉随机干扰，又要求罗经方位对准收敛，因此，分析罗经方位对准的收敛时间特性就显得十分有必要。本文在求得罗经方位对准传递函数的东向陀螺漂移和初始方位误差的频域响应基础上，通过拉普拉斯反变换将其转化成时域响应函数，在时域上针对东向陀螺漂移和初始方位误差对罗经方位对准收敛时间的影响进行了分析。通过分析，主要得出以下结论：

1）通过分析时域响应函数，表明罗经方位对准的收敛时间与陀螺常值漂移、初始方位误差和设置的二阶阻尼震荡周期Td有关。

2）当以0.01 °误差带为收敛判据时，由陀螺常值漂移引起的方位角误差会在至多0.9Td时间内收敛，由初始方位误差引起的方位角误差会在至多1.39Td时间内收敛。

3）当二者共同作用时，对收敛时间起主要作用的是初始方位误差，陀螺常值漂移对收敛时间的影响较小，基本可忽略不计。

本文所提出的方法为设置罗经方位对准相关参数，控制罗经方位对准收敛时间提供了理论依据。