初三数学教学中培养学生函数模型建立能力的实践与研究
2019-10-23蔡魏伟
蔡魏伟
【摘 要】 初三学生已经积累了一定的函数知识,并且具有一定的空间想象力与逻辑思维能力,此时强化函数建模能力培养对于提升学生解题能力具有重要意义。本文结合初三数学《二次函数》教学,重点就函数建模能力培养理念在教学中的渗透策略进行了探讨,希望为后续相关研究与应用提供一些借鉴。
【关键词】 初三数学;函数建模能力;培养策略
建模能力是初中生需要掌握的一种基本解题能力,主要是指学生能否将实际问题转化成对应的数学模型,之后运用相关的数学知识来求解相关问题。而函数作为初中数学教学的重要组成部分,相应的函数模型建立能力培养是进一步提升学生解决函数实际问题的重要保障,强化其专项研究具有重要教育意义。
一、创设问题情景,激发学习兴趣
为了顺利引导学生参与到二次函数模型构建中来,教师需要先创设一些贴合学生生活实际的事情,激发他们的学习兴趣,启发他们积极思考,最终可以通过深入剖析相关问题来建立建模思想。
例1:某旅游机构在自然风景区域当中配备了50辆观光巴士供游客游览使用,假定每辆观光巴士每天最多仅能够租赁一次,且每日的观光巴士租金x(元)为5的倍数。现有如下规律:如果x<100元,那么可以全部租出观光巴士;如果x>100元,每辆观光巴士日租金每增加5元,租出的观光巴士就会相应地减少1辆,且已知道每天全部观光巴士需要耗费1100元管理费,试求:
1.在优惠促销期间,为了全部租出观光巴士且要确保每天不出现亏损,那么每辆观光巴士的日租金至少控制在多少元?
2.为了使每天旅游机构获得最高的租赁净收入,应该将每辆车的日租金定位多少?
解析:该数学题目同学生的实际生活具有紧密联系,是学生外出旅行时常遇到的情况,这样有助于激发他们参与学习的兴趣以及建模的动机。首先,依据“每天全部租出观光巴士后所得的净收入=每天出租观光巴士总收入-每天管理费用”和“净收入为正”等条件,列出求解的不等式,之后结合“每天出租观光巴士净收入=每天观光车辆出租数目×每辆车日租金-每天管理费用”等量关系来分段构建函数模型,其中一段为一次函数模型,另一段则是二次函数模型,之后结合分段函数模型计算来最终的结果。
解:(1)根据题干信息可知,假定全部租出观光巴士,那么可知0
(2)假定每天租赁观光巴士的净收入为y元。
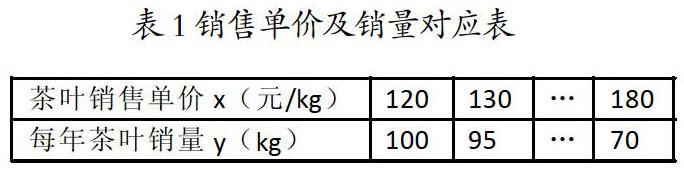
当0 当x>100时,y=(50-(x-100)/5)x-1100=-1/5x2+70x-1100=-1/5(x-175)x2+5025。因为y为二次函数模型,此时可知当x=175时,y取得最大值,最大值为5025元。 二、基于函数模型,解决实际问题 为了进一步强化学生的函数建模意识,深化学生对于函数建模思想的理解和认识,数学教师可以结合实际数学问题,引导学生利用函数模型建构思想来加以解决,使他们可以在利用函数模型解决实际问题的过程中享受到成功的乐趣,并最终逐步掌握这种数学建模思想。 例2:某茶叶店销售的某品牌茶叶的成本价为80元/kg,销售单价≥120元/kg,但<180元/kg,且在销售一段时间后获得,可知该品牌茶叶的销售单价及销量对应表1所示。 假定y和x之间的关系是我们所学过的一种函数关系,试求: 1.试列出函数y和x之间的函数关系式,求出自变量x的范围。 2.为了获得最大的销售利润,茶叶销售价该确定为多少?最大利润为多少? 解析:该道数学题借助表格数据的形式来给出了变量间数量关系,结合数形结合法,配合坐标系中的坐标点,可以直观地确定它们的函数关系为一次函数,之后结合“茶叶销售利润=茶叶销售单价×销售数量”构建求解问题的二次函数模型,最后利用二次函数特性与性质来求解有关问题。 解:(1)由表1可知,茶叶销售单价每增加10元,每天茶叶销售量就减少5kg,所以可知y与x之间呈现为一次函数关系,具体的关系式为:y=100-0.5(x-120)=-0.5x+160,相應的x取值范围为:0≤x≤180。 (2)假定茶叶销售利润为w元,那么w=(x-80)(-0.5x+160)=-1/2x2+200x-12800=-1/2(x-200)2+7200。此时可知当x=180时,销售利润最大,最大值w最大=7000元。 三、注重归纳总结,深化教学目标 初三数学教学期间,在引导学生运用函数模型来解决实际数学问题的同时,还要结合数学教学目标与要求,指导他们归纳和总结相关的函数建模知识,使他们可以对相关的函数模型知识以及脉络进行梳理,并逐步将这些函数模型知识内化于心,确保可以在后续解决实际问题中灵活应用这些知识。此外,在学习期间教师要注意强化小组合作学习,力求可以引导学生相互沟通与交流彼此的函数建模经验与技巧,逐步提升自身的函数建模能力,同时合作学习也可以培养学生的问题意识以及反思能力,最终可以熟练掌握函数建模思想。 总之,二次函数是对我们现实世界中各种变量之间变化规律进行刻画的一种数学模型,是解决现实生活中实际问题的一个重要工具,所以教师必须要高度重视培养学生的函数模型能力。在实际的教学中,教师要注意创设问题情景,激发学习建模兴趣,同时要基于函数模型,解决实际数学问题,并加以归纳、总结,确保提升学生的函数建模能力。
