一个正三角形面积最值的求法探究

许银伙

(福建省泉州外国语中学 362000)

分析一以边OA，OB所在直线分别为x，y轴，建立直角坐标系，通过正三角形的直观性质三边相等和已知条件求出OE，OG的长度关系，进而求出EG的最小值.

△EFG为正三角形，所以|EF|=|EG|=|FG|,

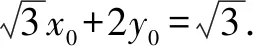
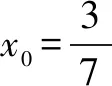
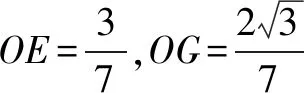
分析二以边OA，OB所在直线分别为x，y轴，建立直角坐标系，深入运用正三角形性质和已知条件求出OE，OG的长度关系，进而求出EG的最小值.

即得：

分析三由图形看出，等边△EFG的边长与∠OEG的大小有联系，考虑寻找它们之间的联系，把△EFG的边长用∠OEG表示， 从而把△EFG面积化为∠OEG的函数，利用三角函数知识解决问题.

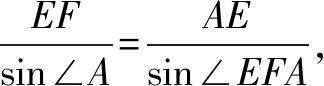
评注1.本方法通过对几何图形深入分析，找出角的相等关系，然后利用正弦定理和已知边的关系，快速得到所求正三角形边长关于引入的角的函数式，从而快速解决问题.利用平面几何知识解题，是高中同学的弱项，值得重视和加强.

分析四由图形看出，若引入直线EF的倾斜角∠AEF=α，可得直线EG的倾斜角∠AEG=α+60°，又因为EF=EG，所以考虑利用直线参数方程中参数的几何意义解题.

因为点G在y轴上，所以x0+rcos(α+60°)=0，即x0=-rcos(α+60°).

评注这种方法运用直线参数方程中参数的几何意义解题，紧扣选修4-4的教材知识，但对三角函数知识要求较高，需要熟练掌握三角函数知识才能完整解答.

分析五由图形看出，若引入直线EF的倾斜角∠AEF=α，可得直线EG的倾斜角∠AEG=α+60°，又因为EF=EG，所以考虑利用向量知识解题.

评注这种方法与方法四类似，但运用的却是必修系列教材的内容，对知识概念的理解和三角函数公式的运用能力要求较高.由此可知：向量与三角函数的结合可以作为解决旋转问题的有力工具.

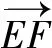
评注这种方法与方法五类似，思路与方法一相同.所运用的知识是原来全国大纲教材关于复数乘法运算的几何意义：若复数为z2对应的向量是复数为z1对应的向量绕逆时针或顺时针旋转θ(θ>0)得到，则z2=z1·(cosθ+isinθ)或z2=z1·[cos(-θ)+isin(-θ)]；如果复数的模长再变为原来的r倍，只需在上面式子右端乘上r即可.它们是解决向量旋转与伸缩的好工具.

以上方法一和方法二求正三角形面积纯粹设点的坐标，不设边长，思路距离问题的解决比较远，运算也比较复杂；方法三设了边长和角，利用平面几何知识和正弦定理，把边长化为角的三角函数，最为扣紧高中核心知识，但平面几何知识的运用是高中学生的弱项；方法四五六都是直接针正三角形边长，分别利用直线参数方程中参数的几何意义，向量与三角函数知识的结合，复数运算的几何意义把边长化为角的三角函数，运算量相对减少.通过这个问题解决方法的探索，可以把高中主要知识融会贯通，有效地提高数学解题能力.