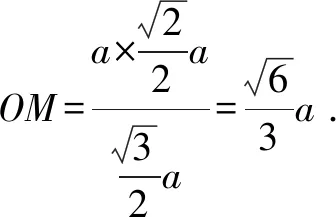正方体在立体几何中的模型作用
2019-10-23王建军郭金红
王建军 郭金红
(1.山西省阳泉市教研室 045000;2山西省阳泉市第二中学校 045000)
正方体是完美的对称图形,是立体几何中的基本模型.正方体中点、线、面之间的位置关系是立体几何的基础,几乎所有的立体几何题型都可以在正方体中找到模型,研究正方体中的立体几何问题可以培养学生的空间观念,理解数学的本质,达到快速解题的目的.
一、正方体中的平行问题
正方体中平行问题证明的思路具有一般性,是证明直线与平面平行,平面与平面平行的通性通法,可以迁移到其他几何体的相关问题学习中.
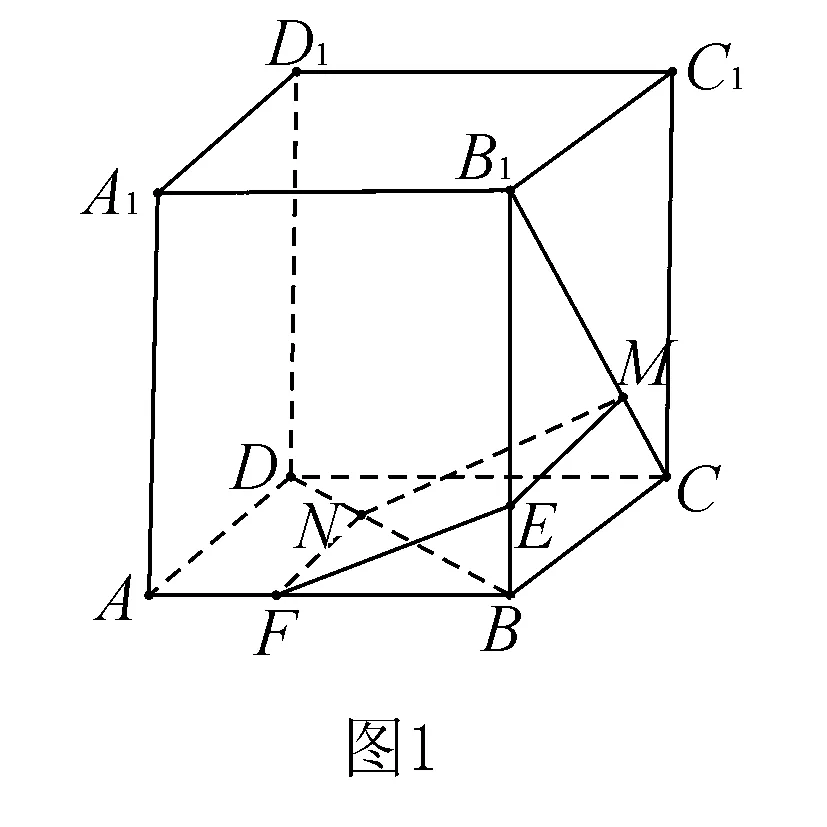
例1如图1,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
分析若能证明MN平行于平面AA1B1B中的一条直线,则依据直线与平面平行的判定定理,MN∥平面AA1B1B.于是有以下添辅助线的方法.
证明如图1,作ME∥BC,交BB1于E;作NF∥AD,交AB于F.连结EF,则EF⊂平面AA1B1B.
∵BD=B1C,DN=CM,
∴B1M=BN.
又ME∥BC∥AD∥NF,∴MEFN为平行四边形.
∴MN∥EF.
又MN⊄平面AA1B1B,EF⊂平面AA1B1B.
∴MN∥平面AA1B1B.
二、正方体中的垂直问题
正方体中隐含着许多线线,线面,面面的垂直关系,我们经常利用三种垂直关系来解题,是立体几何垂直问题的基础,利用正方体解有关线面垂直、面面垂直的问题,思路自然,解法多样.
例2如图2所示,正方体ABCD—A′B′C′D′的棱长为a,M是AD的中点,N是BD′上一点,且D′N∶NB=1∶2,MC与BD交于P.
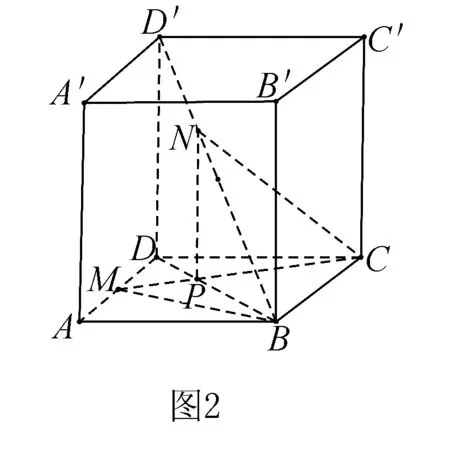
(1)求证:NP⊥平面ABCD;
(2)求平面PNC与平面CC′D′D所成角的正切值.
(3)求点C到平面D′MB的距离.
分析证明直线与平面垂直的方法有多种,最基本的是利用直线与平面垂直的判断定理和平面与平面垂直的性质定理.本题可以根据已知条件得到NP∥DD′,从而利用DD′⊥平面ABCD得证.
解(1)证明:在正方形ABCD中,
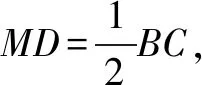
∴DP∶PB=MD∶BC=1∶2.
又已知D′N∶NB=1∶2,
由平行线分线段成比例定理得NP∥DD′.
又DD′⊥平面ABCD,
∴NP⊥平面ABCD.
(2)∵NP∥DD′∥CC′,
∴NP、CC′在同一平面内,CC′为平面NPC与平面CC′D′D所成二面角的棱.
又由CC′⊥平面ABCD,得CC′⊥CD,CC′⊥CM,
∴∠MCD为该二面角的平面角.
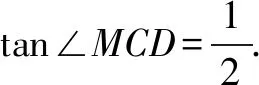

设所求距离为h,即为三棱锥C—D′MB的高.

三、正方体中的角问题
正方体中的异面直线所成的角、线面角、二面角是立体几何中角的代表,搞清正方体中这些角的求解探索过程,可以迁移到其他图形中解决问题.
例3在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.求直线AP与平面BCC1B1所成的角的正切值.
分析直线与平面所成的角是直线与平面关系的基本概念,从概念出发是本题的基本原则,关键是找到平面的垂线.
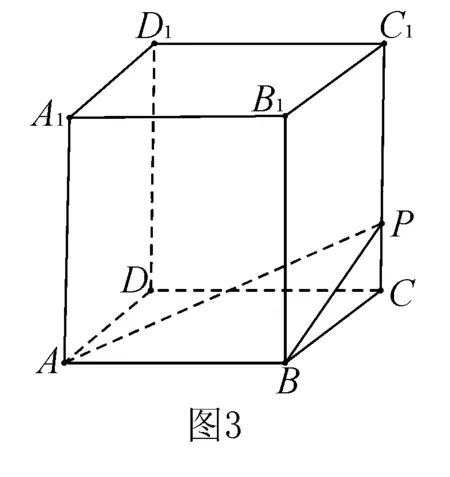
解连结BP.
∵AB⊥平面BCC1B1,
∴AP与平面BCC1B1所成的角就是∠APB,
∵CC1=4CP,CC1=4,∴CP=1.
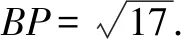
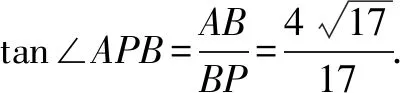

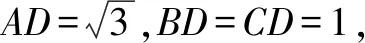
(1)求证:ADBC;
(2)求二面角B-AC-D的余弦值.






∴n1=(x,x,-x).不妨设n1=(1,1,-1).
同理可求得平面ACD的一个法向量为n2=(1,0,-1),
四、正方体中的距离问题
立体几何中的直线到平面的距离、平面到平面的距离最终要转化为点到平面的距离,在转化过程中各种距离的定义起到了关键的作用.
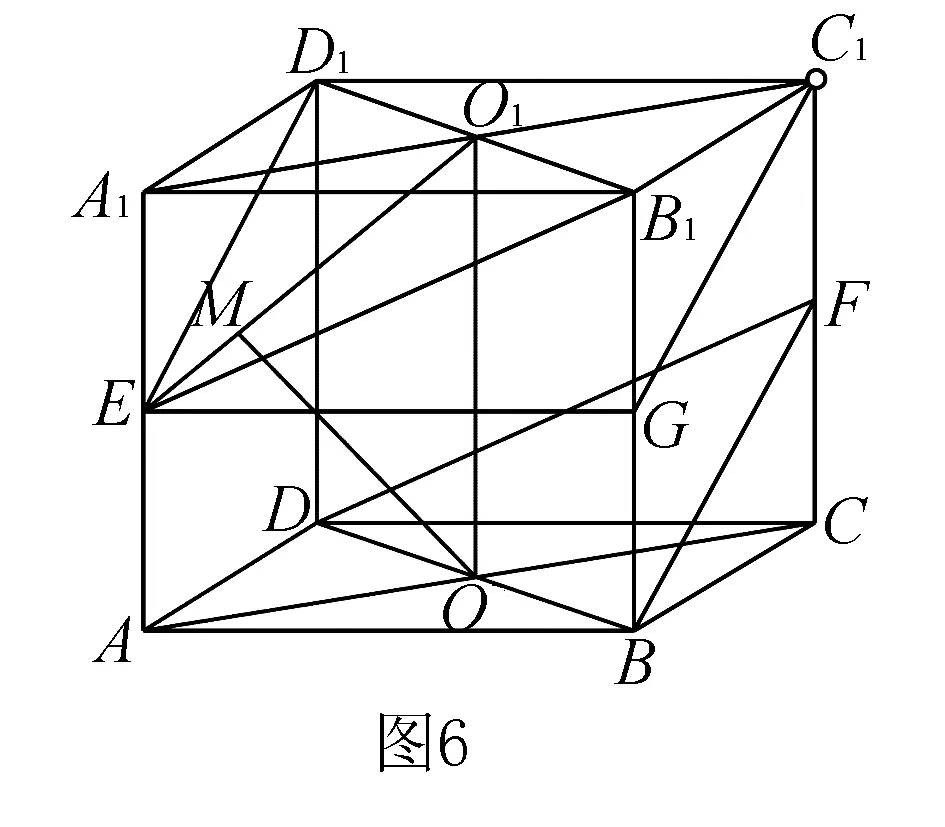
例5正方体ABCD-A1B1C1D1中,E、F分别是AA1,CC1的中点,
(1)求证:平面EB1D1∥平面FBD;
(2)若正方体棱长为a,求平面EB1D1与平面FBD间的距离.
分析证明面面平行要利用平面与平面平行的判定定理,要求平面EB1D1与平面FBD间的距离,根据定义可以在一个平面FBD内找一点作另一个平面的垂线,求出垂线段的长即为距离.
解(1)证明:取BB1的中点G,连接EG,C1G,根据平面几何知识,可得
ED1∥GC1,BF∥GC1,
∴ED1∥BF.
∵ED1⊄平面FBD,BF⊂平面FBD,
∴ED1∥平面FBD.
同样,B1D1∥BD,.
∵B1D1⊄平面FBD,BD⊂平面FBD,
∴B1D1∥平面FBD.
又ED1∩B1D1=D1,∴平面EB1D1∥平面FBD.
(2)连结AC,A1C1,由AC⊥BD,AA1⊥BD,可得
BD⊥平面ACC1A1.
又BD⊂平面FBD,
∴ 平面FBD⊥平面ACC1A1,平面EB1D1⊥平面ACC1A1.
连接O1O,O1E,过点O作OM⊥O1E,则OM⊥平面
EB1D1,OM即为平面EB1D1与平面FBD间的距离.