解决两类立体几何难题的新方法

朱小扣 蓝云波

(1.安徽省无为第三中学城北校区 238351;2.广东省兴宁市第一中学 514500)

《普通高中数学课程标准(2017版)》中指出：“数学学科核心素养包括：数学抽象，逻辑推理，数学建模，直观想象，运算能力，数据分析，这些核心素养既相对独立又相互交融，是一个有机的整体.”而高考的命题势必会考查这些核心素养，这就对学生的空间想象能力，化归能力等能力提出了更高的要求，所以有时在高考立体几何中取得高分非常不容易，有时必须要另辟蹊径.本文将用两个新的方法来解决此类问题，以期抛砖引玉.

一、利用标数法破解三视图问题

对三视图的考查一直是高中数学的重点，往往是通过三视图还原物体的直观图，从而计算直观图的表面积和体积.但还原物体的直观图却是学生学习和教师教学的难点.不少老师在讲解时往往在课件上用不同颜色区分不同的视图所表示的点，笔者觉得这样去教农村的考生而言并不好操作(条件差)，并且在考试时用不同的颜色画点线，重合时也有干扰.为此笔者创造出了“标数法”，举例如下，供大家参考.

例1 (2016年河北省邯郸一模)如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的表面积为( ).

图1

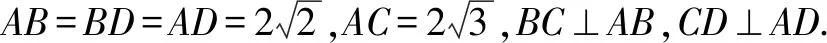
上题如不用标数法，极容易出错.又如：

例2 (2016年安徽省蚌埠一模)某空间几何体的三视图如图所示，则该几何体的体积为( ).

图2

解析如图2，利用正视图，在可能的长方体的顶点上标上“1”；利用侧视图，在可能的长方体的顶点上标上“2”；再利用俯视图，在可能的长方体的顶点上标上“3”，得到了同时拥有“1，2,3”的6个点A,B,C,D,E，F，再经过确认排除点F，于是得到所求几何体是多面体ABCDE：

点评在近几年的各类考试中，以三视图为背景的试题屡见不鲜，且常考常新，应引起高度的重视，但由于学生空间想象力的匮乏，无法迅速地还原出直观图，导致考试丢分.这同样给教师的教学带来麻烦.但如果利用标数法，标上“1”“2”“3”，就可以三位一体，使得问题迅速地，正确地解决.

二、三面角余弦定理破解二面角问题

在做二面角题时，有时不能用常规的方法(如找角法，垂面法，向量法等)来解决时，这时我们可以想想还可用三面角的余弦定理，三面角的余弦定理如下：

1.三面角余弦定理

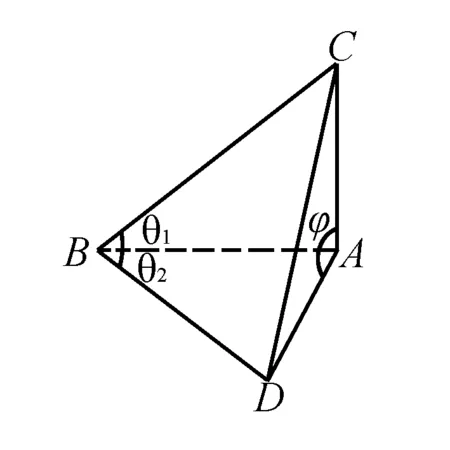
图3

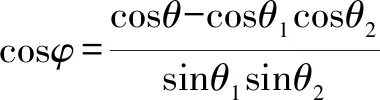
2.三面角定理的应用

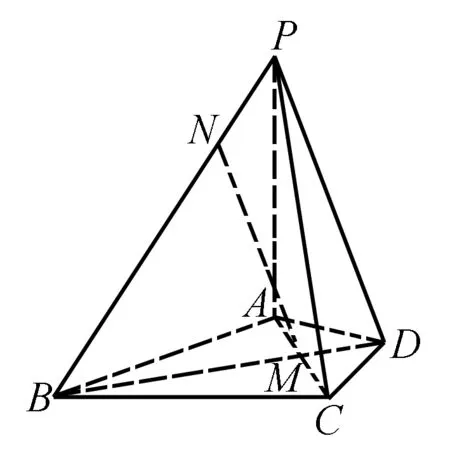
图4

(1)求证：BD⊥PC；

(2)求证：MN∥平面PDC；

(3)求二面角A-PC-B的余弦值.

解析(1)(2)(略).

故由三面角的余弦定理定理得：

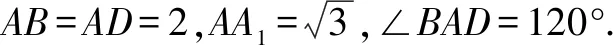
图5 图6

(1)求异面直线A1B与AC1所成角的余弦值；

(2)求二面角B-A1D-A的正弦值.

点评通过三面角的余弦定理，可以迅速地解决二面角问题，也可以弥补学生空间想象能力的不足.需要注意的是,三个角的位置不能搞混乱，才开始写的时候可以用图3“照葫芦画瓢”，多写几次就能熟练地掌握.

总结高考是选拔人才的考试，想取得高分，仅仅对知识达到初步的理解和掌握还是不行的，必须加以延拓并灵活运用.可能有的老师对介绍本文的“超纲”知识，并不认同，但正如不管是发现法教学，还是探究法，抛锚法，范例法等方法来教学，如果仅仅依靠某一种或几种教学方法，就能达到学生能力的提高，我觉得也是“教条主义”.教无定法，学无定法，解题亦无定法.