浅析用动量定理处理平均安培力问题的几个典型案例

刘 冰

(广西壮族自治区博白县中学 537600)

在分析电磁感应动力学问题时，常遇到安培力的变力问题，此类问题用牛顿第二定律结合运动学或动能定理的思维都无法或很难解决，但利用动量定理处理变力的思路问题就迎刃而解.

图1

案例一两根足够长的固定的平行金属导轨位于同一水平面内，两导轨间的距离为L，在导轨上面垂直于导轨放置两根导体棒ab和cd，构成矩形回路，如图1所示.两根导体棒的质量均为m，电阻均为R，回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场，磁感应强度为B，两导体棒均可沿导轨无摩擦地滑行.开始时，固定棒cd，用水平恒力F拉ab棒，使之由静止开始向右加速运动位移为S时，速度恰好达到最大.求：

(1)ab棒所能达到的最大速度是多少？

(2)当ab棒的速度为最大速度的一半时，ab棒的加速度是多少？

(3)当ab棒的速度达到最大速度时，突然撤去力F并同时释放cd棒，从ab开始运动至两棒速度稳定时，电路中共产生的热量以及通过导体横截面的电量各是多少？

(4)从cd棒开始运动到两棒速度稳定时，两棒之间增大的距离是多少？

(3)释放cd棒后至两棒共速的过程中，ab棒和cd棒所受的安培力等大反向，两棒组成的系统动量守恒，

由动量守恒得：mvm=2mv

ab棒由静止开始至速度最大的过程中，设通过导体横截面的电量q1，由法拉第电磁感应定律得：

从释放cd棒至两棒共速的过程中设通过导体横截面的电量q2

(4)设从cd棒开始运动到两棒速度稳定时，两棒之间增大的距离为Δx.此过程对cd棒由动量定理得：

案例二如图2所示，光滑水平面上停放一小车，车上固定一边长为L=0.5 m的正方形金属框abcd，金属框的总电阻R=0.25Ω，小车与金属框的总质量m=0.5 kg，在小车的右侧，有一宽度大于金属框边长，具有理想边界的匀强磁场，磁感应强度B=1.0T，方向水平且与线框平面垂直，现给小车一水平速度使其向右运动并能穿过磁场，当车上线框的ab边刚进入磁场时，测得小车的加速度a=10 m/s2.求：(1)金属框刚进入磁场时，小车的速度为多大？

(2)从金属框刚进入磁场开始，到其完全离开磁场，框中产生的焦耳热为多少？

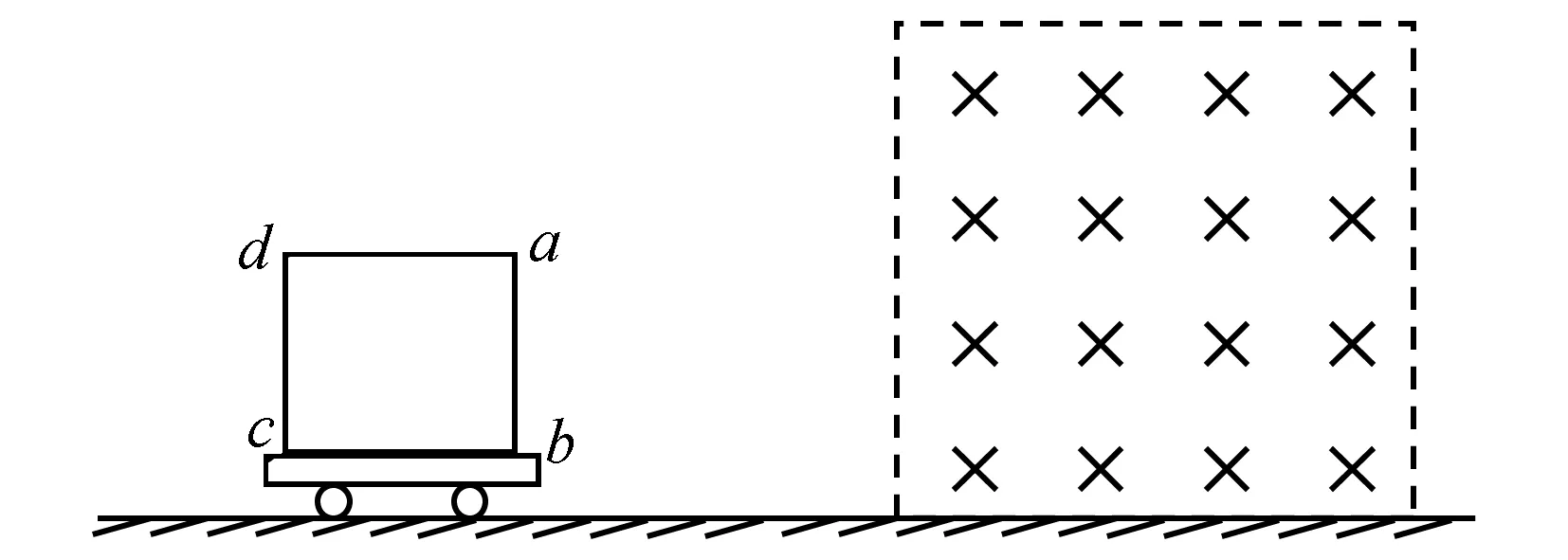
图2

解析(1)设小车初速度为v0，则金属框进入磁场时，ab边由于切割磁感线产生的电动势为：E=BLv0

根据牛顿定律：BIL=ma

由以上三式可解得：v0=5 m/s

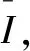
由上两式得v1=4 m/s

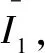
由上两式得v2=3 m/s

由以上各式解得Q=4.0 J

图3

A．金属棒a的质量ma=0.5 kg

B．t1时间内和t2时间内通过金属棒a某一横截面的电荷量之比为3∶2

C．a、b两金属棒最终均做匀速直线运动，速度均为4m/s，稳定后回路中电流为0

D．从开始运动至达到稳定状态，金属棒a上产生的焦耳热为8J，金属棒b上产生的焦耳热为4 J

答案:CD