用对立统一的观点来探究函数图象的变换

陈玉田

(福建省仙游县第二中学 351200)

函数图象的平移、伸缩、对称等变换在中学数学里扮演了一个特殊的角色，为便于掌握，有些教辅总结出一些变换规律，并记为“左加右减，上加下减”.但笔者认为，这些规律其实并没有看清图象变换的本质，带有机械性和局限性，以为不可取；进而认为教材中讨论函数y=Asin(ωx+φ)图象的变换也甚为不妥；同时发现，用对立统一的观点来理解、记忆函数图象的变换更具一般性，可操作性，更能体会到数学思想的作用.下面就让咱们一起一窥函数图象变换的端倪，为方便见，我们分别讨论平移、伸缩、对称变换.

一、平移变换

先讨论把函数y=f(x)所表示的图象向左平移k(k>0，以下均同)个单位后，要如何改变其表达式？假定点A(a，b)是函数上一点，那么图象向左平移k个单位后，观察坐标系可知点A移到了相应点A1(a-k，b)，显然，平移后的函数为y=f(x+k).即是把表达式中x变为x+k，注意到k>0，且坐标系的x轴为左负右正，这不就是我们常说的“左加右减”么.

辩证法认为，世上万物都是对立且统一的.上文中“负移正加”这种现象也是一种对立统一，那么它是偶然的呢，或是必然？深入思考：把图象向左(其实质是沿x轴负方向)平移k个单位，这时候，在对应法则不变情况下，取较小的数(因假定k>0，故有此说)就达到了原来的效果，因此，要把y=f(x)改为y=f(x+k).换个说法，用加上一个数去克服向左平移而导致自变量变小的矛盾.同样，把图象y=f(x)向右平移k个单位应是y=f(x-k)；而把图象y=f(x)向下平移k个单位，其实质是沿y轴负方向平移k个单位，依上述对立原理，应当改变函数表达式中的y为y+k，即改为y+k=f(x).故我们有：

定理1(函数图象平移变换定理)函数y=f(x)的图象沿x轴平移改变x，沿y轴平移改变y，且沿负方向平移k个单位就加上k，沿正方向平移k个单位就减去k.

具体说就是：若图象y=f(x)左右平移时(其实质是沿x轴平移)，要改变表达式中的x，且遵照“往负向移用加，往正向移用减”的原则；若图象y=f(x)上下平移时(其实质是沿y轴平移)，要改变表达式中的y，也遵照“往负向移用加，往正向移用减”的原则.用口诀可记为：左右变x，上下换y，左加右减，下加上减.

分析几道例题：

例1函数y=2x+1的图象向右平移1个单位后是____；向下平移2个单位后是____.

分析：向右，就是沿x轴，要改变x，并且是正方向，用减.即x→x-1.向下，就是沿y轴，要改变y，并且是负方向，用加，即y→y+2.

解新函数分别是：y=2(x-1)+1,即y=2x-1；y+2=2x+1,即y=2x-1.切记，分别是用x-1去代替原来式中的x，用y+2去代替原来式中的y.

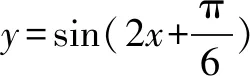
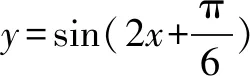
例3 函数y=3x2-2x+1的图象向左平移1个单位后，再向上平移2个单位后得到____.

分析按常规要先配方.其实，毋须如此费事，由定理1：向左平移1个单位，就是将所有的x→x+1；向上平移2个单位，就是将所有的y→y-2.

解平移后得到y-2=3(x+1)2-2(x+1)+1整理即得.

详述至此，细心的读者会发现，这里不过是将原规律的“上加下减”改为“下加上减”.可是，莫小看这一变动，它体现了x、y两条不同坐标轴的对立统一，具有普遍性，自然应适用于伸缩变换.我们知道，教材中讨论y=Asin(ωx+φ)时，A>1与0<ω<1都用伸长变换，这种不一致必然给我们的理解与记忆带来麻烦和负担.那么，对伸缩变换能否也淡化x、y的不同，从而将它们统一起来呢？答案是肯定的.

二、伸缩变换

考虑把图象y=f(x)变换为图象y=Af(kx)(A>0，k>0).这里头含有两种变换：①x→kx，②y→by，其中，b=1/A.由倍数关系要用伸缩变换，结合教材，对照平移变换的分析，利用对立统一原理不难得出：

变换①要这样进行：图象上所有点的横坐标变为原来的1/k，纵坐标不变(k>1时，缩为原来的1/k；0

变换②要这样进行：图象上所有点的纵坐标变为原来的1/b，横坐标不变(b>1时，缩为原来的1/b；0

需要指出的是，这里作了b=1/A，使得y轴上的伸缩变换用b来刻画，就与x轴上的伸缩变换高度一致，同时也体现了对立思想：大于1是缩短，小于1是伸长.故有：

定理2(函数图象伸缩变换定理)若函数y=f(x)图象上各点的纵(横)坐标不变，横(纵)坐标变为原来的1/k，就相应地改变表达式中的x(或y)，且遵循倒数原则：x→kx(y→ky).即：y=f(kx)(或ky=f(x)).反之亦真.

可记为：横x纵y，小伸大缩(大小相对1而言).当然，可以把平移、伸缩变换合起来记为：横x纵y，负移正加，小伸大缩，对立统一.

例4把y=sinx上所有的点的纵坐标不变，横坐标____就可以得到函数y=sin(x/4)的图象.

分析比较知，x→x/4.

解伸长到原来的4倍.

例5若函数y=sinx的图象上各点的纵坐标伸长为原来的3倍，而横坐标不变，再将其向上平移2个单位，得到____.

此外，利用两个定理，处理平移、伸缩的次序问题那便不费吹灰之力了，如：

前文提到，这种图象变换思想具一般性，所以定理可推广到多元函数的图象、曲线等变换.这时候，原来前人所总结的口诀就束手无策了.如：

例7将抛物线y2=4x向下平移3个单位，再向左平移2个单位后，得到____；将x3+y3=3axy(叶形线)上各点横坐标不变，纵坐标变为原来的1/3，所得到的图形为____.

解①(y+3)2=4(x+2);②x3+(3y)3=9axy.

三、对称、翻折变换

因篇幅所限，对对称、翻折变换不再加以讨论，这里只给出结果(函数图象或曲线对称变换定理)，请读者朋友们验证.

定理3-1f(x,y)=0的图象沿y轴(直线x=0)或沿x轴(直线y=0)翻折后，得到f(-x,y)=0或f(x,-y)=0.

定理3-2f(x,y)=0的图象沿直线x=a或沿直线y=b翻折后，得到f(2a-x,y)=0或f(x,2b-y)=0.

如前所述，这些定理也可推广到多元函数、曲线变换等，实在是一劳永逸了.

结束本文之前，不妨请读者们再注意文中定理之结构与几道例题的解答，整齐划一，在高度的严谨中渗透着内在和谐之美.也因如此，笔者以为，不应把函数图象变换的x、y轴分离开来，而应积极地在看似孤立的现象中寻找联系，寻找共同点，从而把它们统一起来，方为正道！