相对运动法在高中物理追及相遇问题中的妙用

林海生

(福建省莆田第十中学 351146 )

首先让我们先研究相对于静止参考系A所做的运动，在此平面中同时存在B、C两个物体，相对于A做直线运动，若B相对于A的运动为牵连运动，C相对于A的运动为绝对运动，则C相对于B的运动称之为相对运动.

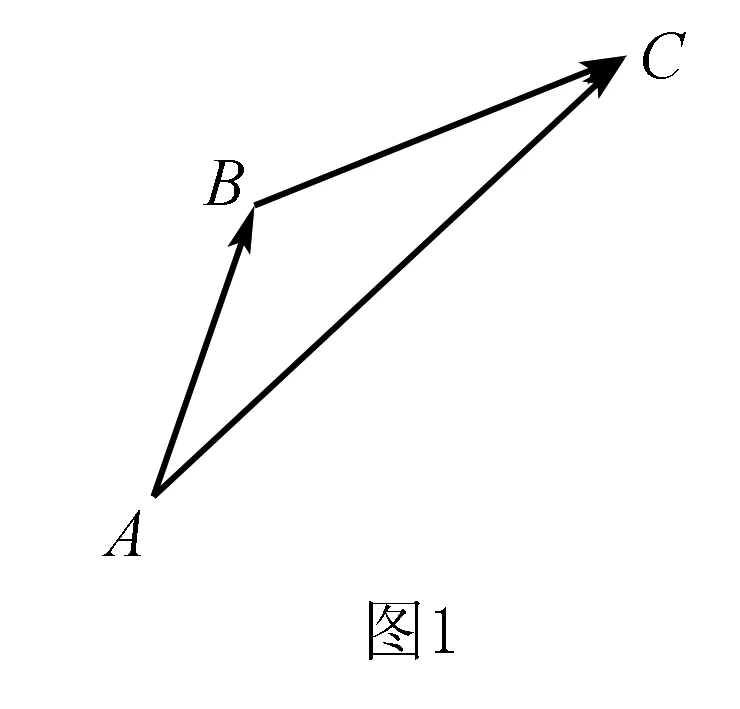
由图1可知 绝对运动=牵连运动+相对运动

可进一步写成：S相对=S绝对-S牵连

两边同时对t微商有：v相对=v绝对-v牵连

两边再次对t微商有：

a相对=a绝对-a牵连

应用相对运动法进行解题技巧性很高，需要一定的空间想象能力，掌握这种方法较为困难，下面通过一些例题来讲解这种方法的应用

一、一维追及相遇问题

例1如图2所示，A、B两棒长均为L=1 m，A的下端和B的上端相距h=20 m，若A、B同时运动，A做自由落体运动，B做竖直上抛运动，初速度v0=40 m/s，求： (1)A、B两棒何时相遇；(2)从相遇开始到分离所需的时间．

分析选择自由落体运动A为参考系，则

v相对=vB-vA=v0-0=v0

a相对=aB-aA=g-g=0

由此可知B相对于A向上做匀速直线运动

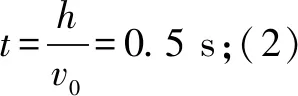
例2一辆汽车在十字路口遇红灯，当绿灯亮时汽车以4 m/s2的加速度开始行驶，恰在此时，一辆摩托车以10 m/s的速度匀速驶来与汽车同向行驶，汽车在后追摩托车，求：(1)汽车从路口开始加速起动，在追上摩托车之前两车相距的最大距离是多少；(2)汽车经过多少时间能追上摩托车?

分析以汽车为参考系，则

v相对=v摩托-v汽车=10-0=10 m/s

a相对=a摩托-a汽车=0-4=-4 m/s2

由此可知摩托车做初速度为10 m/s，加速度为-4 m/s2的匀减速直线运动，当摩拖车相对速度减为0时，两者距离最大；当摩擦车相对位移为0时，两者发生相遇.

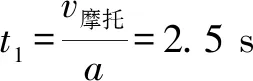
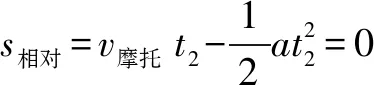
二、二维追及相遇问题

例题3水平面内有两个距离为L的物体A和B，A朝着B做速度为vA的匀速直线运动，B朝着垂直于AB所在直线的方向做速度为vB的匀速直线运动，试求AB之间的最小距离d.

分析以B为参考系，则在A水平方向有vx相对=0-vB=-vB,在竖直方向有vy相对=vA-0=vA.故A相对B的运动轨迹如图4所示,通过分析几何关系即可得到最小距离d.

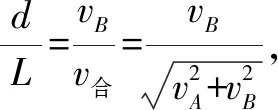
例4如图5，物体甲从高为H处以速度v1平抛，同时乙从距甲水平距离为S处由地面以初速度v2竖直上抛，不计空气阻力，则甲乙两物体相遇的条件是( ).

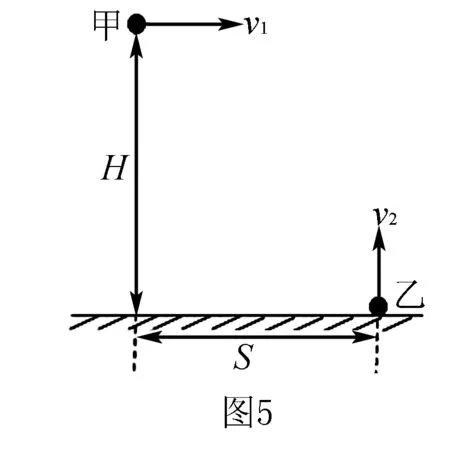
A.从抛出到相遇的时间为H/v2

B.若要在物体乙上升过程中遇甲，必须S/v1=H/v2，v22>gH

C.若要在物体乙下降过程中遇甲，必须S/v1=H/v2，2v22>gH

D.若相遇点离地面的高度为H/2，则v22=gH

分析以平抛运动物体甲为参考系，竖直上抛乙物体

在水平方向有：vx相对=0-v1=-v1

在竖直方向有：vy相对=v2-0=v2

a相对=a2-a1=g-g=0

由此可知乙相对甲水平方向向左做匀速，在竖直方向向上做匀速.

解答以甲为参考系，对乙有S=v1tH=v2t

采用相对运动法来分析物体间的追及相遇问题，尤其在二维中有极大地简便性.此外二维的追及相遇中需要综合分析水平和竖直两个方向的相对运动性质才可进一步作答.