例析中考中的“全等三角形”试题
2019-10-22文肖学军
文肖学军
在历年的中考试题中,考查全等三角形应用的试题比比皆是,拟以近年来部分省市的中考试题为例加以说明,给同学们热身练笔。
一、直接考查三角形是否全等
例1(2018·四川成都)如图1,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )。
A.∠A=∠DB.∠ACB=∠DBC
C.AC=DBD.AB=DC
【解析】本题已知∠ABC=∠DCB,图中有一条公共边BC=CB可以使用,一般不能用来判断三角形全等的条件只有“边边角”即“SSA”,于是容易知道选项C是正确的。
【点评】本题主要考查全等三角形的判断方法。用“边边角”判定三角形全等是一些同学常犯的错误之一,要引起重视。在证明三角形全等时,特别要注意利用题设或挖掘图形中隐藏的条件,如公共边、公共角、部分线段相等等。
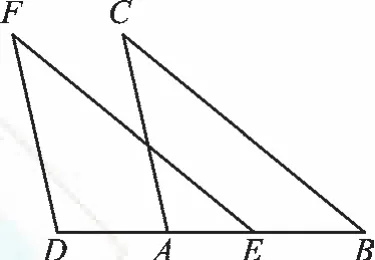
图2
二、证明两角或者两边相等
例2 (2018·四川泸州)如图2,EF=BC,DF=AC,DA=EB。求证:∠F=∠C。
【解析】要证明∠F=∠C,只需证明△ABC≌△DEF即可。由于题设条件中已经具备两组对应边相等这一条件,只要将DA=BE转化为DE=AB,即可利用“边边边”定理加以证明。
【点评】本题主要考查全等三角形的简单应用,题设条件DA=BE不可以直接使用,必须要转化为两边相等的条件。
例3(2019·陕西)如图3,点A、E、F、B在直线l上,AE=BF,AC∥BD,且AC=BD。求证:CF=DE。
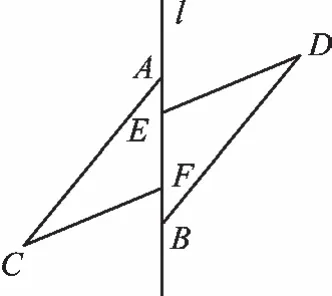
图3
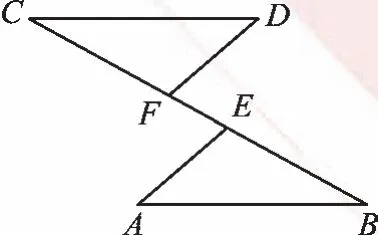
图4
【解析】要证明CF=DE,只要证明△ACF≌△BDE即可。由条件AC∥BD,可得∠CAF=∠DBE;又由AE=BF得到AF=BE,而AC=BD,利用“边角边”定理可得△ACF≌△BDE。
【点评】本题主要考查了全等三角形的判定和性质。证明线段和角相等常常需要先证明有关的三角形全等。
三、探求两边之间的关系
例4(2018·山东菏泽改编)如图4,AB∥CD,AB=CD,CE=BF。请写出DF与AE之间的关系,并证明你的结论。
【解析】DF与AE之间的关系为平行且相等。由题设条件,用“边角边”容易证明△CDF≌△BAE,从而有DF=AE和∠CFD=∠BEA;根据“等角的补角相等”,得到∠DFE=∠AEF,于是有DF∥AE。结论成立。
【点评】两边之间的关系分为位置关系和数量关系两种。位置关系一般为平行或垂直,数量关系为相等或者倍数。
【变式】本题若连接DE、AF,则图中还存在哪些全等三角形?你能够证明吗?请大家试一试。遇到较为复杂问题时,常需要证明两组或者多组三角形全等,本题变式便是一例。
四、计算边长和角度
例5(2018·江苏南京)如图5,AB⊥CD,且AB=CD。E、F是AD上两点,CE⊥AD,BF⊥AD。若CE=a,BF=b,EF=c,则AD的长为( )。
A.a+cB.b+c
C.a-b+cD.a+b-c

图5

图6
【解析】在Rt△ABF和Rt△CDE中,因为AB⊥CD,CE⊥AD,BF⊥AD,所以∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,于是有∠A=∠C。又因为AB=CD,从而△ABF≌△CDE。又因为BF=DE=b,EF=c,故有AD=AF+DF=a+(b-c)=a+b-c。因此答案选D。
例6(2019·湖北宜昌)如图6,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE。
(1)求证:△ABE≌△DBE;(2)若∠A=100°,∠C=50°,求∠AEB的度数。
【解析】(1)由角平分线定义得出∠ABE=∠DBE,由“边角边”定理证明△ABE≌△DBE即可;(2)由三角形内角和定理得出∠ABC=30°,由角平分线定义得出15°,在△ABE中,由三角形内角和定理即可得出答案。
【点评】例5和例6都考查了全等三角形的判定与性质,例6还考查了角平分线的定义、三角形内角和定理。熟练掌握相关概念、证明三角形全等是解题的关键。
五、考查全等三角形的综合应用
例7 (2019·北京)如图7,已知锐角∠AOB,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧PQ,交射线OB于点D,连接CD;(2)分别以点C、D为圆心,CD长为半径作弧,交弧PQ于点M、N;(3)连接OM、MN。根据以上作图过程及所作图形,下列结论中错误的是( )。
A.∠COM=∠COD
B.若OM=MN,则∠AOB=20°
C.MN∥CDD.MN=3CD

图7
【解析】连接ON,由作图可知△COM≌△COD。可得∠COM=∠COD,故A正确。若OM=MN,则△OMN为等边三角形,由全等可知,∠COM=∠COD=∠DON=20°,故B正确。由题意知,OC=OD,∴∠OCD=设OC、OD与MN分别交于R、S,易证△MOR≌△NOS,则OR=OS,∴∠ORS=∴∠OCD=∠ORS,∴MN∥CD,故C正确。又由题意,易证MC=CD=DN,∴MC+CD+DN=3CD。∵两点之间线段最短,∴MN<MC+CD+DN=3CD,故答案选D。
【点评】本题以常见的锐角为背景,通过画弧构建图形,着重考查了全等三角形的判定和性质、等边三角形、三角形内角和定理、平行线的判定、两点之间线段最短公理等众多数学概念和定理,将许多看似没有联系的知识点巧妙地连接在一起,立意较好,不失为一道匠心独运的好题!
