35CrMo钢高温流变行为及其本构方程
2019-10-21胡希磊韩鹏彪鲁素玲孟致安王同会王浩
胡希磊 韩鹏彪 鲁素玲 孟致安 王同会 王浩


摘 要:為了更好地描述35CrMo钢应力-应变关系,建立材料的本构模型,采用Gleeble3800热模拟试验机对热轧后的35CrMo钢进行了热模拟高温压缩实验,研究了35CrMo钢在变形温度为800,900,1 000,1 100,1 200 ℃,应变速率分别为0.01,0.1,1,10 s-1的条件下,变形温度和应变速率对材料流变应力的影响。实验结果表明:35CrMo钢高温变形时存在动态回复型与动态再结晶型两种应力-应变关系,通过求解材料临界应变与峰值应变的关系,间接建立了35CrMo钢峰值应力本构方程,并验证了其准确性。所提出的本构方程可以较好地描述35CrMo钢热变形条件下的应力-应变关系,对于35CrMo钢的热成形工艺设计及数值模拟工作具有基础理论意义。
关键词:黑色金属及其合金;35CrMo钢;热变形;本构方程;热模拟实验
中图分类号:TG136.2 文献标志码:A
文章编号:1008-1542(2019)04-0351-08
材料的高温流变本构方程是有限元模拟时计算物体应力-应变关系的基础,是提高模拟精度、计算力能参数、合理制定锻造工艺的关键[1-2]。35CrMo钢为合金结构钢,具有较高的抗冲击韧性、疲劳强度以及静力强度,淬透性高,具有良好的综合性能[3],可用于生产各种承受冲击、弯扭、高载荷的设备零件及各种大型受力构件,在钢结构、工程机械和船舶制造等领域有广泛应用。目前,已经有很多关于35CrMo钢热变形行为的研究[4-8],然而关于建立热轧后35CrMo钢高温流变本构方程的文章鲜有报道。通过35CrMo钢高温压缩热模拟实验,研究变形温度和变形速率对35CrMo钢流动应力的影响,建立了35CrMo钢高温变形条件下双曲正弦形式的Arrhenius本构方程,为后续反挤压成形过程模拟提供了模型参数。
1 实验材料与方法
1.1 实验材料
实验采用热轧后的35CrMo钢,其化学成分见表1。
1.2 实验方法
实验在Gleeble3800热模拟试验机上完成,由于35CrMo钢锻造温度为800~1 200 ℃,实验变形温度设定为800,900,1 000,1 100,1 200 ℃,应变速率为0.01,0.1,1,10 s-1。采用单向压缩,变形量为60%,具体的高温压缩过程如图1所示。试样首先以10 ℃/s的速度加热到1 200 ℃,保温6 min,再以10 ℃/s的速度降至变形温度,保温2 min以消除内部温度梯度,然后进行热压缩实验,实验结束后水淬冷却。
2 实验结果及分析
2.1 材料的流变行为
图2为不同温度及应变速率下,35CrMo钢热压缩的真应力-真应变曲线。从图2可以看到在变形初期,真应力-真应变曲线变化趋势基本相同,即真应变不断增加,真应力随之增加并达到峰值;在此之后,真应力-真应变曲线呈现两种不同的变化趋势[9-10]。
1)在应变速率为0.01 s-1、变形温度为900~1 200 ℃,应变速率为0.1 s-1、变形温度为1 000~1 200 ℃,应变速率为1 s-1、变形温度为1 100 ℃,1 200 ℃,应变速率为10 s-1、变形温度为1 200 ℃时,真应力与真应变呈现动态再结晶型曲线关系,即在曲线达到峰值后,真应力随真应变的增加而缓慢降低至某一稳态。这是由于加工硬化的强化作用小于动态回复与动态再结晶的软化作用,因此整体呈现为真应力-真应变曲线的降低。
2)应变速率为0.01 s-1、变形温度为800 ℃,应变速率为0.1 s-1、变形温度为800~900 ℃,应变速率为1 s-1、变形温度为800~1 000 ℃,应变速率为10 s-1、变形温度为800~1 100 ℃时,真应力与真应变呈现动态回复型曲线关系。其峰值应力随着真应变的增大而继续增大,这说明变形体内加工硬化的强化作用要大于动态回复的软化作用,曲线持续上升。
动态回复型真应力-真应变曲线不存在明显的应力峰值,需借助求取曲线临界应变εc的方式间接建立35CrMo钢高温变形条件下的峰值应力本构方程[10]。通过求取动态再结晶临界应变εc,再根据临界应变εc=αεp[11-12](其中εp为峰值应变,α为相关系数),获得动态再结晶型的峰值应变εp。
2.2 临界应变的确定
临界应变εc由材料加工硬化率θ与真应变σ的变化规律来确定。SELLARS[12]指出变形材料在化学成分、原始晶粒恒定的条件下,动态再结晶临界条件仅与变形条件(应变温度T和应变速率[AKε·])有关。陈学文等[13]和POLIAK等[14]认为材料发生再结晶时,其θ-σ曲线所呈现的拐点就是临界应变εc。动态再结晶临界条件的计算方法有很多,其中POLIAK等[14]和王一成等[15]根据热力学不可逆原理的动力学临界条件提出,将达到应力-应变曲线峰值点前的θ-σ散点图进行三次多项式拟合,即:
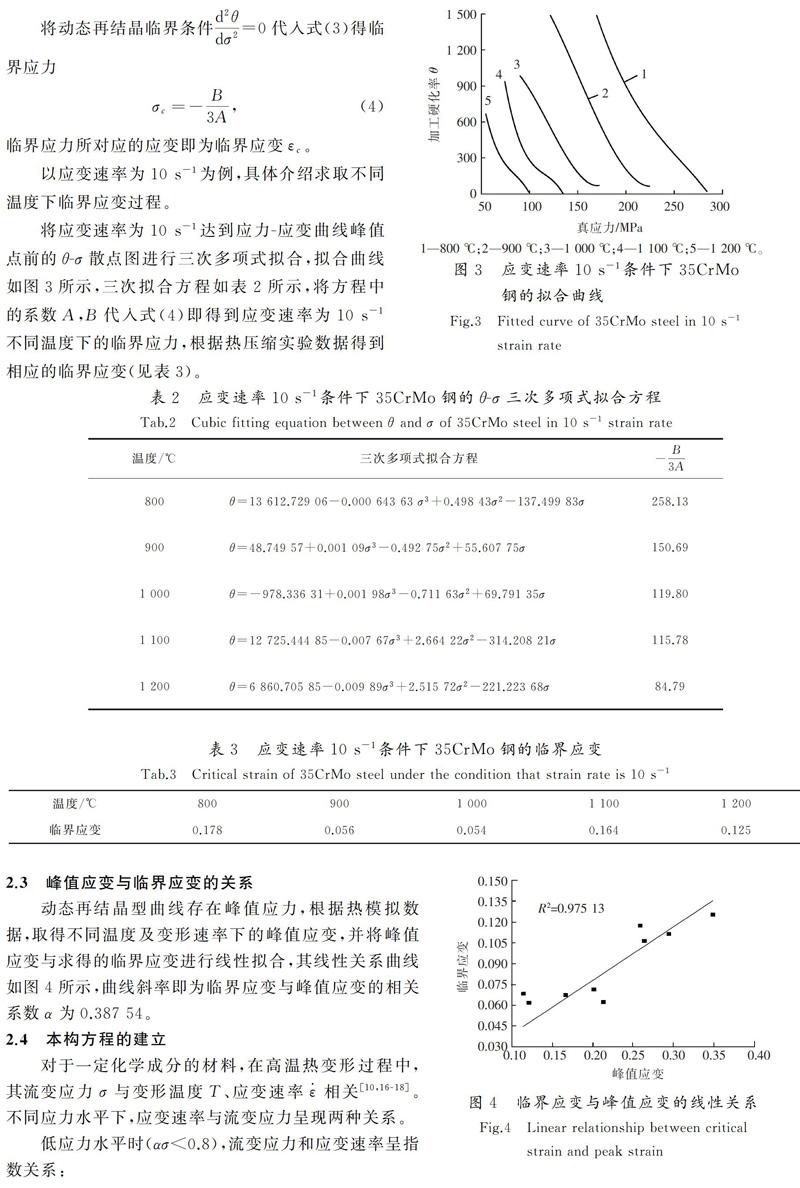
以应变速率为10 s-1为例,具体介绍求取不同温度下临界应变过程。
将应变速率为10 s-1达到应力-应变曲线峰值点前的θ-σ散点图进行三次多项式拟合,拟合曲线如图3所示,三次拟合方程如表2所示,将方程中的系数A,B代入式(4)即得到应变速率为10 s-1不同温度下的临界应力,根据热压缩实验数据得到相应的临界应变(见表3)。
2.3 峰值应变与临界应变的关系
动态再结晶型曲线存在峰值应力,根据热模拟数据,取得不同温度及变形速率下的峰值应变,并将峰值应变与求得的临界应变进行线性拟合,其线性关系曲线如图4所示,曲线斜率即为临界应变与峰值应变的相关系数α为0.387 54。
2.4 本構方程的建立
对于一定化学成分的材料,在高温热变形过程中,其流变应力σ与变形温度T、应变速率[AKε·]相关[10,16-18]。不同应力水平下,应变速率与流变应力呈现两种关系。
2.4.2 变形激活能的确定
当变形速率一定时,整理式(8)可得:
为了验证构建的35CrMo钢的双曲正弦形式Arrhenius本构方程的准确性和可靠性,利用所建立的本构方程,计算出不同变形条件下的峰值应力理论值,并计算出实验值与计算值的相对误差。峰值应力实验值与计算值统计表见表4,其中相对误差最大值为5.14%,说明本文所建立的本构方程可以较好地描述35CrMo钢热变形条件下的应力-应变关系。
3)利用所建立的本构方程,计算出不同变形条件下的峰值应力理论值,同实验值相比较,相对误差最大值为5.14%,说明该本构方程可以很好地描述35CrMo钢热变形条件下的应力-应变关系。
4)主要研究了35CrMo钢高温变形条件下的应力-应变关系,因此该本构方程仅适用于热变形,对于温变形或冷变形条件下35CrMo钢的应力-应变关系还有待进一步研究。
参考文献/References:
[1] 冀晓磊,韩鹏彪,鲁素玲,等.基于DEFORM的索具接头内孔反挤压成形数值模拟[J].河北科技大学学报,2017,38(4):383-388.
JI Xiaolei, HAN Pengbiao, LU Suling, et al.Numerical simulation for inverse extrusion forming of the hole of a rigging joint based on DEFORM[J].Journal of Hebei University of Science and Technology, 2017, 38(4):383-388.
[2] 肖政兵,黄元春,刘宇.基于微观机理的电磁铸造35CrMo钢的高温流变本构方程[J].金属热处理,2017,42(1):1-8.
XIAO Zhengbing, HUANG Yuanchun, LIU Yu. Physically-based constitutive model for high temperature deformation of electromagnetic casted 35CrMo steel[J].Heat Treatment of Metals, 2017,42(1):1-8.
[3] 黄元春,王三星,肖政兵,等.不同条件高温压缩变形后35CrMo钢的显微组织[J].机械工程材料,2017,41(6):84-89.
HUANG Yuanchun, WANG Sanxing, XIAO Zhengbing, et al. Microstructures of 35CrMo steel after high-temperature compression deformation under different conditions[J]. Materials for Mechanical Engineering, 2017,41(6):84-89.
[4] 郭会光,张巧丽,游晓红,等.35CrMo钢热变形机制的模拟研究[J].大型铸锻件,2000(2):22-25.
GUO Huiguang, ZHANG Qiaoli, YOU Xiaohong, et al. Simulated research on hot forming mechanism of 35CrMo steel[J]. Heavy Castings and Forgings,2000(2):22-25.
[5] 张斌,李波,张鸿冰.35CrMo钢动态再结晶过程数值模拟与试验研究[J].锻压技术,2004(6):36-39.
ZHANG Bin, LI Bo, ZHANG Hongbing. Value simulation and experiment study of dynamic re-crystal process of 35CrMo steel[J]. Forging & Stamping Technology,2004(6):36-39.
[6] 王进,陈军,张斌,等.35CrMo结构钢热塑性变形流动应力模型[J].上海交通大学学报,2005,39(11):1784-1786.
WANG Jin, CHEN Jun, ZHANG Bin, et al. The flow stress model of 35CrMo structural steel during hot forming[J]. Journal of Shanghai Jiaotong University,2005,39(11):1784-1786.
[7] 张斌,张鸿冰.35CrMo结构钢的热变形行为[J].金属学报,2004,40(10):1109-1114.
ZHANG Bin, ZHANG Hongbing. Hot deformation behavior of 35CrMo steel[J].Acta Metallurgica Sinica,2004,40(10):1109-1114.
[8] 叶健松,徐祖耀.35CrMo钢动态再结晶的实验研究与数值模拟[J].轧钢,2004,21(5):23-27.
YE Jiansong, XU Zuyao. Experimental research and numerical simulation of dynamic recrystallization of 35CrMo steel[J]. Steel Rolling, 2004,21(5):23-27.
[9] 杨莉. 300M钢热变形工艺研究[D]. 焦作:河南理工大学,2016.
YANG Li. Study on Hot Deformation Process of 300M Steel[D].Jiaozuo:Henan Polytechnic University,2016.
[10]章晓婷,黄亮,李建军,等.300M高强钢高温流变行为及本构方程[J].中南大学学报(自然科学版),2017,48(6):1439-1447.
ZHANG Xiaoting, HUANG Liang, LI Jianjun, et al. Flow behaviors and constitutive model of 300M high strength steel at elevated temperature[J]. Journal of Central South University (Science and Technology),2017,48(6):1439-1447.
[11]黄顺喆,厉勇,王春旭,等.高强渗碳钢高温热变形的本构方程[J].材料热处理学报,2014,35(10):210-217.
HUANG Shunzhe, LI Yong, WANG Chunxu, et al. Constitutive equations of a high-strength carburizing steel during high temperature thermal deformation[J]. Transactions of Materials and Heat Treatment,2014,35(10):210-217.
[12]SELLARS C M. Computer modelling of hot-working processes[J]. Materials Science and Technology, 1985, 1(4):325-332.
[13]陈学文,陈天安,周会军,等.45Cr4NiMoV合金动态再结晶临界应变[J].材料热处理学报,2015,36(1):109-113.
CHEN Xuewen, CHEN Tianan, ZHOU Huijun,et al. Critical strain of dynamic recrystallization of 45Cr4NiMoV steel[J].Transactions of Materials and Heat Treatment,2015,36(1):109-113.
[14]POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J]. Acta Materialia, 1996, 44(1):127-136.
[15]王一成,李峰.AISI1215钢动态再结晶临界应力应变的确定方法[J].安徽工业大学学报(自然科学版),2015,32(1):1-6.
WANG Yicheng, LI Feng. Methods of determining the critical stress or strain for initiation of dynamic recrystallization in AISI1215 steel[J]. Journal of Anhui University of Technology (Natural Science),2015,32(1):1-6.
[16]JONAS J J, SELLARS C M, TEGART W J M. Strength and structure under hot-working conditions[J]. Metallurgical Reviews, 1969, 14(1):1-24.
[17]ZENER C, HOLLOMON J H. Problems in non-elastic deformation of metals[J]. Journal of Applied Physics, 1946, 17(2):69-82.
[18]TAKUDA H, FUJIMOTO H, HATTA N. Modelling on flow stress of Mg-Al-Zn alloys at elevated temperatures[J]. Journal of Materials Processing Technology, 1998, 80:513-516.
[19]郝慶乐,韩静涛,宋晶杰,等.高强硼钢高温变形行为及其本构方程的建立[J].金属热处理,2016,41(2):131-135.
HAO Qingle, HAN Jingtao, SONG Jingjie, et al. Deformation behavior at high temperature and establishment of constitutive equation of high strength boron steel[J]. Heat Treatment of Metals, 2016,41(2):131-135.
[20]谭智林,向嵩.Q690低碳微合金钢热变形行为及动态再结晶临界应变[J].材料热处理学报,2013,34(5):42-46.
TAN Zhilin, XIANG Song. Behavior of hot deformation and critical strain for dynamic recrystallization of a Q690 low carbon microalloyed steel[J]. Transactions of Materials and Heat Treatment, 2013, 34(5):42-46.
[21]ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1):22-32.
