考虑磁致伸缩效应的偏转式发电机的振动特性研究

李争 杜磊 杨凯 刘令旗 董维超

摘 要：为了提高风能利用率，解决现有开关磁阻发电机转子旋转的单一性问题，提出一种新型可偏转双定子开关磁阻式风力发电机。首先，基于电磁-固体力学模块，建立定子结构磁固耦合数值模型，对电磁场、磁通密度、磁致伸缩密度进行了理论分析。其次，采用有限元平台对发电机进行了直观建模，基于力学理论建立考虑磁致伸缩效应的电磁-固体力学基本方程。最后，通过有限元法对发电机内、外双定子以及转子自转、偏转进行磁固耦合仿真，得到应力分布及对应的振动位移。仿真结果表明：磁致伸缩效应下的振动位移属纳米级别且所受应力较小，对发电机运行影响可忽略不计。磁固耦合的分析方法可为分析电机振动、进一步优化发电机参数提供理论参考。

关键词：电磁固体力学;磁固耦合;振动位移;双定子;磁致伸缩效应

中图分类号：TM352;O348.8 文献标志码：A

文章编号：1008-1542（2019）04-0325-08

开关磁阻式风力发电机具有结构简单、启动风速低、输出电能稳定等特性，因此在风力发电领域具有广阔的应用前景和较高的研究价值。双定子结构的发电机响应快、可高精度定位、过载能力强，在发电机本体结构和外界风速一定的情况下，其工作效率可大大提高。同时，根据以往可偏转多自由度电机[1-5]具有高效、灵活性高等优点，提出了一种可偏转双定子开关磁阻式发电机，其主要特征除了采用转子双侧具有齿槽式结构的转子和双定子进行设计外，还利用转子两侧连接的液压控制台来调节发电机的转向，以适应不同风向，提高风能利用率。

但随着人民物质生活水平的提高，人们对低振动噪声电机的需求越来越高，严重的振动和噪声会浪费能量，降低电机效率，阻碍其在一些场合的推广。对于电机电磁振动噪声的研究起源于20世纪30年代，基本上都是从电磁力的角度进行研究。1842年由英国学者JOULE[6]首先发现磁致伸缩效应，主要体现在结构场和电磁场之间，即：磁固耦合;文献[7—8]指出磁致伸缩现象是磁性材料处于磁场中并被磁化时，沿其磁化方向出现的缩短及伸长变化，表现为振动效果;文献[9—10]对电机的定子进行了受力分析，建立了二维非线性稳态有限元模型，分析了由磁致伸缩效应导致的电机定子形变;文献[11—12]从磁固耦合角度对发电机定子结构的振动开展了研究工作，取得了较系统的研究成果。文献[13—14]得出磁致伸缩力是电机定子结构应力的主要来源及振动因素，并且对无取向硅钢片在正弦及谐波激励下的磁化和磁致伸缩特性曲线进行了测量。因此，考虑磁致伸缩效应可以使模型更加完善精确，便于对电机进行结构的优化设计。

笔者在前人研究的基础上研究了可偏转双定子开关磁阻式发电机在结构力学和电磁场中的振动问题，利用comsol有限元软件对其进行仿真分析，最后得出发电机的磁通密度、双定子所受应力及振动位移等参数，其结果可为进一步优化发电机提供理论参考。

1 可偏转双定子开关磁阻式发电机的结构参数及控制机理

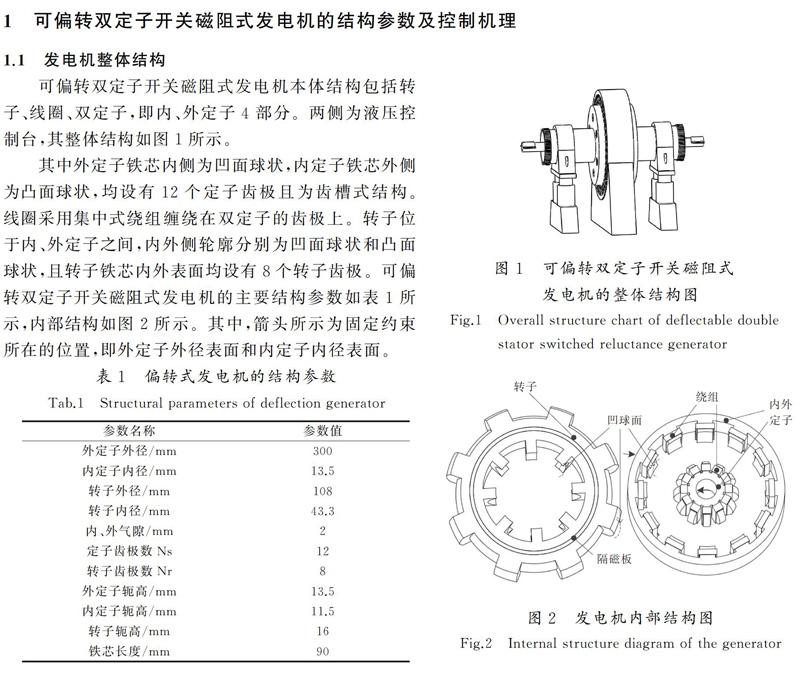
1.1 发电机整体结构

1.2 发电机的控制机理

根据发电机本体结构，可将其近似看成由内外两台发电机组成，分别是外定子、内转子组成一台内转子开关磁阻发电机;内定子、外转子组成一台外转子开关磁阻发电机。由于该发电机的结构为内、外双定子，所以须采用两套外控电路来分别连接内定子绕组（D，E，F）和外定子绕组（A，B，C）。该发电机转子由原动机拖动旋转，控制电机实现励磁和发电续流状态转换。如图3所示为发电机控制电路，承担着励磁功率输入与发电功率输出的双重任务，采用他励工作模式确保能提供稳定的励磁电压。其中励磁电压源Uc为100 V，二极管VD1，VD2，VD5，VD6，VD9，VD10确保励磁阶段电源向绕组供电，其余的二极管则为电感储存能量向负载供电提供通道。S1—S6是6个导通开关，由驱动电路控制其导通顺序。

规定逆时针方向为电机旋转正方向，当转子位置角为17.5°～27.5°，内定子D相绕组导通;当转子位置角为25°～35°，外定子B相绕组导通。本文选取转子位置角为38°，此时转子相对于外定子处于中间位置，即转子齿极与外定子齿极有部分重合的时刻，内定子的D相绕组与外定子的B相绕组处于同时发电状态，其中，B相绕组发电电流为25 A，D相绕组发电电流为13 A。图4所示为转子逆时针转过38°时绕组发电时的结构图。

2 发电机定子结构的磁固耦合数值模型

发电机B，D相绕组发电后，在电机内部产生磁势，进而在定子凸极与转子凸极之间的气隙建立电磁场，根据磁阻最小原理，定转子气隙间产生电磁力，其中径向电磁力会引起定子系统的电磁振动[15-19]，具体表现为定子系统受到应力后会产生振动位移现象。本文建立了电磁-固体力学耦合数值模型，并利用有限元法对磁致伸缩效应导致的电机定子结构振动特性进行了计算与分析。

2.1 磁场分析

电机绕组的磁场方程如式（1）所示：

2.2 磁致伸缩应力分析

使用弹性力学方法分析电机的振动特性，利用达朗贝尔原理等效惯性力及阻尼力的结构力学基本方程如式（2）所示：

磁致伸缩应变可由磁感应强度B与单值磁致伸缩特性曲线插值计算得出[20]。定转子气隙中的磁场是引起振动的主要原因[21-22]。

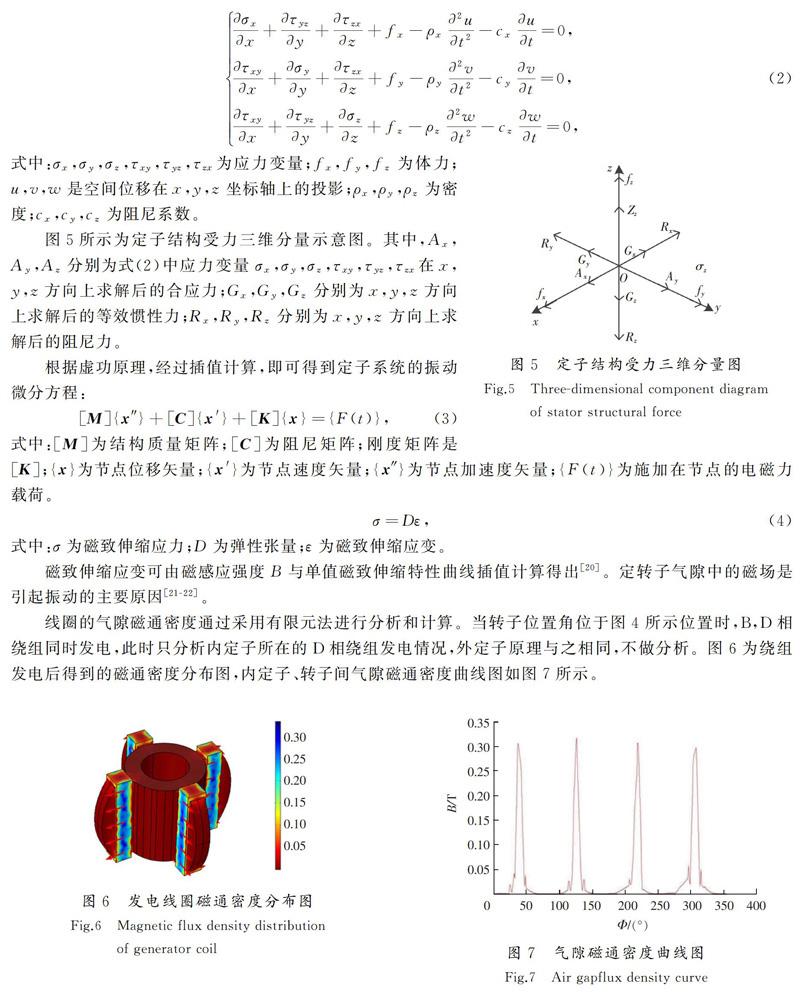
线圈的气隙磁通密度通过采用有限元法进行分析和计算。当转子位置角位于图4所示位置时，B，D相绕组同时发电，此时只分析内定子所在的D相绕组发电情况，外定子原理与之相同，不做分析。图6为绕组发电后得到的磁通密度分布图，内定子、转子间气隙磁通密度曲线图如图7所示。

观察图6和图7可知，3D圖形与曲线相对应。磁密最大值出现在发电绕组周围。定转子处于中间位置时磁阻最小，磁力线最密集，磁通密度最大，约为0.32 T。其中，当4个D相绕组同时发电时，绕组会在电流的作用下显现磁性。从图6中面上箭头可知，相邻绕组显示不同磁性，磁通密度方向相反;相隔绕组显示相同磁性，磁通密度方向相同。

图8所示为外定子、转子间气隙磁通密度B沿空间角度θ，Φ变化的分布图。其中气隙磁通密度B随θ角的变化周期为60°，在一个变化周期内，B的变化曲线呈矩形分布，对应于磁力线N极发出，流向同相相隔两侧的S极。磁通密度B沿Φ角的分布波形周期为360°，有2个波峰2个波谷，对应一个周期内发电机转子齿极与内定子齿极部分重合，即内定子4个D相绕组发电时，此时磁通密度最大值为0.32 T。通过对比发现磁密最大值及分布情况与图6相一致，由于在电磁力激励下电机模块的振动位移是电机机械变形的主要来源，这为下文研究由于电磁力导致的定子结构振动与位移奠定了良好基础。

3 定子结构振动位移与所受应力分析

3.1 外定子分析

为了在有限元分析中得到定子系统所受应力及振动位移情况，对电磁场、磁致伸缩应力、磁通密度进行理论分析。

由于本发电机为可偏转双定子式结构，本节先分析发电线圈对外定子结构振动特性的影响。其中，在有限元仿真中，将外定子与外定子壳表面的接触部分设置为边界条件，即固定约束，如图2左侧箭头所示。当外定子上的B相绕组发电后，发电机外定子结构引起的应力和所引起的振动位移如图9—图11所示。图10为外定子外径所在位置的位移曲线，外定子结构整体位移情况如图11所示。

由图9分析可知，外定子结构上不同位置所受的应力大小不同，主要集中分布在缠绕在定子齿上的4个B相发电绕组，所受最大应力为1.5×104 N/m2。与定子齿相接触的外定子轭部所受应力相比较小。观察图10可知，发电机定子结构受力产生的振动位移主要集中在4个B相发电绕组周围，与定子结构所受应力相对应。显示相同磁性的发电绕组的振动位移相近，相差不到0.02 mm，最大位移仅为0.06 mm。

从图11可以看出，发电绕组发电产生电磁场后，对外定子结构产生的振动位移最大仅为0.12 mm，对发电机工作的影响可忽略不计。

3.2 内定子分析

上节分析了发电线圈对外定子结构振动特性的影响。同理，将内定子与内定子轴接触部分设为边界条件，如图2右侧箭头所示。此外，本发电机内定子上共有12个内定子齿，根据图8分析可知，4个B相线圈发电后，对外定子结构的影响只集中在与之接触的外定子齿、外定子轭部，对相邻的定子齿没有影响。所以本节只分析内定子齿上4个D相发电绕组的发电情况，其余8个内定子齿及绕组由于不发电不做研究。发电机内定子结构引起的应力和所引起的位移如图12—15所示。

观察图12和图13看出，所受应力大的地方产生的振动位移大，内定子外径的振动位移主要集中在4个D相发电绕组四周。其中内定子所受最大应力为2.5×103 N/m2。由此导致的最大振动位移约为0.016 mm。由于内定子绕组发电电流为13 A，比外定子发电绕组所发电流小，所受最大应力与振动位移均比外定子的小，与实际情况相吻合。

如图14所示为内定子齿位移曲线图，走势呈左右对称，最大位移为0.106 mm。由于内定子齿离发电绕组近，所以其振动位移比图13中内定子外径的振动位移略大。内定子整体在电磁力作用下压缩或扩张导致的最大位移为0.1 mm，对发电机的工作几乎无影响。

分析图15可知，显示相同磁性的相隔发电绕组由于振动位移情况相近，与实际相符，最大位移为0.1 mm。

3.3 内、外双定子分析

3.3.1 内、外双定子自转分析

当发电机转子绕xy平面自转到如图4所示位置时，内、外双定子上相对应的B，D绕组同时发电，交变的气隙磁场产生电磁力，铁磁材料中的磁畴由杂乱无章变为沿着磁力线的方向压缩或扩张。内、外双定子结构及转子同时会受到应力及产生振动位移的影响。

当B，D相绕组发电，定转子气隙间产生的电磁力波引起定子结构振动的同时，会对气隙长度产生影响，即发生振动位移。反之，定转子间气隙长度的改变也会影响电磁力的大小。在磁场和振动位移场的相互影响作用下，导致发电机自转时，其所受应力较不考虑磁场、振动位移场相互影响时小，约为2×103 N/m2。通过观察图16可知，在转子齿和内外定子齿部分重合区域，也存在受力情况。

3.3.2 内、外双定子偏转分析

当发电机转子以y方向为轴，偏转9°时，得到如图16所示在偏转情况下，内、外双定子所受应力及转子受应力三维图，如图17所示。

当发电机工作在风力场合时，外界风迫使液压控制台升降，与之相连的转子实现偏转。此时研究绕y轴偏转9°时的工况，内、外定子齿与转子齿处于部分重合状态，致使接触面积不同，B，D相8个绕组发电电流也出现变化;另外磁致伸缩的大小不仅与定子结构所处的磁场大小有关，还与磁场的方向有关，不同电流产生不同的交变气隙磁场，致使偏转时所受最大应力如图17所示为1.8 N/m2，低于自转时所受应力。

4 结 论

本文提出的新型可偏转双定子开关磁阻式发电机，采用内、外双定子，利用液压升降台控制转子实现多自由度偏转，可满足不同风向的要求。

基于电磁-固体力学模块，通过建立定子结构磁固耦合数值模型，对磁场、磁通密度、磁致伸缩应力进行理论分析，采用有限元平台对发电机进行了直观建模，系统阐述了基于磁致伸缩效应下的定子系统所受应力，并计算了内、外双定子、内定子齿的振动情况，且均属于纳米级位移。其中定子结构中的定子轭部与定子齿所受应力较大，因此，对于电机的设计，应增加材料的強度，才有利于提高发电机运行稳定性及降低振动噪声，计算和分析的结果可为电机的优化设计提供了理论依据。

未来还需完善可偏转双定子开关磁阻式风力发电机中的偏转运动状态的振动研究，并将继续对影响发电机振动的温度场-应力场进行研究，以达到降低噪声、优化电机结构的目的。

参考文献/References：

[1] 李争，王咏涛，葛荣亮，等.永磁球形多自由度电机研究进展综述[J].微电机，2011，44（9）：66-70.

LI Zheng， WANG Yongtao， GE Rongliang， et al. The summary and latest research of PM spherical M-DOF motor [J]. Micromotors， 2011， 44（9）：66-70.

[2] 王群京，李争，陈丽霞，等.一种永磁球形步进电动机的运动分析与仿真[J].系统仿真学报， 2005，17（9）：2260-2264.

WANG Qunjing， LI Zheng， CHEN Lixia， et al. Kinematic analysis and simulation of permanent magnet spherical stepper motor[J]. Acta Simulata Systematica Sinica， 2005，17（9）：2260-2264.

[3] 夏长亮，李洪凤，宋鹏，等.基于Halbach阵列的永磁球形电动机磁场[J].电工技术学报， 2007， 22（7）：126-130.

XIA Changliang， LI Hongfeng， SONG Peng， et al. Magnetic field model of a PM spherical motor based on Halbach array[J].Transactions of China Electrotechnical Society， 2007， 22（7）：126-130.

[4] 李争，郭智虎，张玥.新型永磁转子偏转式三自由度电机磁场特性分析[J].河北科技大学学报， 2012， 33（5）：422-428.

LI  Zheng， GUO Zhihu， ZHANG Yue .Magnetic field analysis of a novel 3-DOF deflection type PM motor[J]. Journal of Hebei University of Science and Technology， 2012， 33（5）：422-428.

[5] 李争，邢殿辉，乜玮，等.永磁转子偏转式三自由度电机热特性分析[J].河北科技大学学报， 2015， 36（3）：279-285.

LI Zheng， XING Dianhui， NIE Wei， et al. Thermal characteristics analysis of  a novel 3-DOF deflection type PM motor[J]. Journal of Hebei University of Science and Technology， 2015， 36（3）： 279-285.

[6]    JOULE J P. On a new class of magnetic forces[J]. Electr  Magn Chem，1842，8：219-224.

[7] 祝麗花，杨庆新，闫荣格，等.考虑磁致伸缩效应电力变压器振动噪声的研究[J].电工技术学报， 2013， 28（4）：1-6.

ZHU Lihua， YANG Qingxin， YAN Rongge， et al. Research on vibration and noise of power transformer cores including magnetostriction effects[J].Transactions of China Electrotechnical Society，2013，28（4）：1-6.

[8] HUANG Xuzhen， TAN Qiang， LI Liyi， et al. Winding temperature field model considering void ratio and temperature rise of a permanent magnet synchronous motor with high current density[J] .IEEE Transactions on Industrial Electronics， 2017，64（3）：2168-2177.

[9] MOHAMMED O A， CALVERT T， MCCONNELL R. Coupled magnetoelastic finite element formulation including anisotropic reluctivity tensor and magnetostriction effects for machinery applications[J]. IEEE Transactions on Magnetics， 2001， 37（5）：3388-3392.

[10]HILGERT T G D， VANDEVELDE L， MELKEBEEK J A A. Numerical analysis of the contribution of magnetic forces and magnetostriction to the vibrations in induction machines[J]. Iet Science Measurement & Technology， 2007， 1（1）：21-24.

[11]胡宇达，邱家俊，黄良.大型发电机定子端部绕组的电磁特性[J].机械强度，2006，28（1）：20-24.

HU Yuda， QIU Jiajun， HUANG Liang. Electromagentic characteristics on stator end windings of large turbo-generator[J]. Journal of Mechanical Strength， 2006， 28（1）：20-24.

[12]张式勤，刘芸芸，吴建华.开关磁阻电机定子振动的有限元分析[J]. 中小型电机，2004，31（1）：5-8.

ZHANG Shiqin， LIU Yunyun， WU Jianhua. FEM analysis of stator vibration behavior for switched reluctance motors[J]. S & M Electric Machines， 2004，31（1）：5-8.

[13] 张欣，解超群，祝丽花，等. 考虑磁致伸缩效应的电机应力数值仿真与实验[J]. 电工技术学报， 2017，32（增2）：50-55.

ZHANG Xin， XIE Chaoqun， ZHU Lihua， et al. Numerical simulation and experimental research on stress of motor including magnetostriction effects[J]. Transactions of China Electrotechnical Society， 2017，32（sup2）：50-55.

[14] 贲彤，陈龙，闫荣格，等.考虑磁化及磁致伸缩特性各向异性的感应电机铁心电磁应力分析[J].电工技术学报，2019，34（1）：66-74.

BEN Tong， CHENG Long， YAN Rongge， et al. Stress analysis of induction motor core considering anisotropic magnetic and magnetostrictive properties [J]. Transactions of China Electrotechnical Society， 2019. 34（1）：66-74.

[15]DENG Zhangxian， DAPINO M. Review of magnetostrictive vibration energy harvesters[J]. Smart Materials and Structures， 2017， 26（10）：aa8347.

[16] VICTOR M， PAAVO R， FLORAN M， et al. Effect of magnetic forces and magnetostriction on the stator vibrations of a bearingless synchronous reluctance motor[J]. IEEE Transactions on Magnetics， 2019，55（6）：2894739.

[17]李争，高世豪，张岩，等.基于电场感应的水下无线电力传输[J].河北科技大学学报，2018，39（6）：552-558.

LI Zheng， GAO Shihao， ZHANG Yan， et al. Underwater radio power transmission based on electric field inductuon[J]. Journal of Hebei University of Science and Technology， 2018，39（6）：552-558.

[18]邱家俊.电机的机电耦联与磁固耦合非线性振动研究[J].中国电机工程学报，2002，22（5）：109-115.

QIU Jiajun. Investigation on coupled mechanical and electrical vibration and coupled magnetical and solid vibration of electrical machine[J]. Proceedings of the CSEE，2002， 22（5）：109-115.

[19]BEN Tong， YANG Qingxin， YAN Rongge， et al. Stress analysis of inverter-fed induction motor considering anisotropic magnetization and magnetostrictive properties[J]. IEEE Transactions on Applied Superconductivity， 2018，28（3）：5204904.

[20]ZHU Lihua，WANG Bin， YAN Rongge， et al. Numerical and experimental research of electromagnetic vibration of motor core including magnetostriction under different rotation speed[J]. IEEE Transactions on Magnetics，2015，52（3）：8102004.

[21]張磊， 刘闯， 王云林，等. 开关磁阻电机磁链特性检测与位置信号估计[J]. 电机与控制学报， 2013， 17（2）：28-33.

ZHANG Lei， LIU Chuang， WANG Yunlin， et al. Flux linkage characteristic detection of switched reluctance motor and the position estimate[J]. Electric Machines and Control， 2013，17（2）：28-33.

[22]王雅玲， 徐衍亮， 刘西全. 双定子永磁同步发电机（I）——结构原理及其响应面法设计[J]. 电工技术学报， 2011， 26（7）：167-172.

WANG Yalin， XU Yanliang， LIU Xiquan. Dual-stator permanent magnet synchronous generator （Ⅰ）：Schematic structure and design based on response surface method[J]. Transactions of China Electrotechnical Society， 2011， 26（7）：167-172.