基于偏移定位技术的水利探测方法及应用

吴学礼 郑文俭 胡雪松 孟凡华 甄然 武晓晶

摘 要：为了抑制探地雷达原始图像中较为强烈的直达波，突显较弱的目标信号，实现对隐患位置的精确定位，提出了结合鲁棒主成分分析的Stolt偏移方法。首先使用探地雷达分析程序包matGPR3.1生成合成数据，模拟坝体和坝体内空洞模型，通过扫描处理得到探地雷达原始图像，然后利用鲁棒主成分分析方法提取目标双曲线信号，最后采用Stolt偏移技术对目标信号进行聚焦处理，并通过最小熵速度估计选取合适的偏移速度得到最佳偏移效果。实验结果表明，提出的方法能够有效地抑制杂波，更清楚地判别目标空洞的位置。与之前方法相比，其得到的图像分辨率更高，性能更优，在水利工程隐患探测方面具有一定的应用价值。

关键词：空间物理探测;探地雷达;鲁棒主成分分析;Stolt偏移;最小熵

中图分类号：TP751;P631.8 文献标志码：A

文章编号：1008-1542（2019）04-0317-08

水利关乎国民经济的发展，水利工程的安全隐患问题是一个亟待解决的重点问题。水利工程隐患一般有堤坝渗漏、坝体裂缝、坝体内空洞等，这些隐患的存在使人们的生命财产安全受到了严重威胁，而探地雷达（ground penetrating radar，GPR）作为一种无损高效的地球物理探测手段，能够实时显示地下剖面图像，直观反映出工程的实际情况，在水利工程隐患探测方面有着很好的应用前景[1-2]。

探地雷达通过发射高频电磁波并接收反射回波再由计算机处理得到雷达图像[3]，但是，探地雷达接收到的回波图像中往往有杂波存在，这导致很难准确判读有用信息，因此，有效消除这些杂波非常必要。国内外学者已经研究出很多抑制杂波的方法，均值法是最为常见的杂波抑制方法，但其处理结果往往会造成图像中的信息丢失。基于时频域的方法如离散余弦变换、曲线变换和小波变换等，这些方法都较大程度上抑制了杂波但仍存在缺陷。目前，基于子空间域的杂波抑制方法最为有效，申家全等[4]提出了基于主成分分析（principal component analysis，PCA）自动选择准则的杂波抑制方法，但是当地下介质较为复杂时鲁棒性较差，抑制效果不理想。ZHANG等[5]提出了一种基于鲁棒主成分分析（robust principal component analysis，RPCA）探地雷达成像方法，通过将杂波分量和目标分量用稀疏低秩表示来有效分离杂波。 SONG等[6]提出了基于鲁棒主成分分析的快速筛选方法应用于杀伤人员地雷的检测。鲁棒主成分分析方法可以弥补PCA方法的不足以及其他方法的缺陷等问题，提高了探测性能。

然而上述研究只能抑制杂波，对于目标信号的散射现象无效。在探地雷达实际工程应用中，由于其收发天线波束具有一定的宽度，致使地下目标回波图像与实际位置和形状产生偏差。通常目标回波显示为双曲线，为了精确获取目标的实际位置则需要应用偏移技术进行处理。偏移技术是通过将探地雷达记录的波场进行反向延拓來实现偏移成像，其方法包括很多种，如Stolt偏移[7-9]、 有限差分偏移[10]、克希霍夫偏移[11-12]等。然而，在对探地雷达数据做偏移处理时，偏移效果的好坏与电磁波在介质中传播的速度有关。速度过小，将导致双曲线收敛不充分，聚焦不完全;速度过大，将会产生过聚焦现象，双曲线拖尾上翘。针对这类问题，修志杰等[13]利用偏移技术结合最小熵方法估计速度得到了很好的效果。ZHOU等[14]提出使用F-K滤波器结合最小熵技术实现了目标的准确定位。

本文提出了一种结合鲁棒主成分分析的Stolt偏移方法，通过仿真实验验证了其有效性，不仅可以有效抑制杂波，而且可以提高雷达图像分辨率实现精准定位，为探测水利工程隐患的精确位置提供了很大帮助。

1 鲁棒主成分分析算法

鲁棒主成分分析算法是一种基于压缩感知和稀疏表达理论的信号处理方法，它的思想是将观测数据矩阵分成一个低秩矩阵和一个稀疏矩阵之和，目前该算法已经应用于目标检测等许多领域[15]。在探地雷达二维原始数据中，杂波具有低阶特性可以近似为低秩矩阵，而目标通常是稀疏的可以近似为稀疏矩阵。假设探地雷达原始数据矩阵为[WTHX]D，它可以分解为

2.2 最小熵速度估计

偏移效果是否理想与电磁波在介质中的传播速度有关。如果偏移速度比实际速度小，则双曲线收敛不充分，聚焦不完全;如果偏移速度比实际速度大，则会出现过聚焦现象，双曲线拖尾上翘。合理的速度参数会改善目标图像的聚焦效果，使之定位精确。为了定量评价偏移效果的好坏，XU等[17]提出了一种基于熵最小化的频率波数偏移成像方法，引入图像熵的概念和偏移技术相结合用于估算地下介质的波速。

根据上述定义可知，对于单道探地雷达数据来说，当只包含一个单幅脉冲时，熵值取得最大值 1，单幅的脉冲越多，熵值就越小。对于一幅图像而言，其熵值的大小代表了图像的清晰程度。熵值越大，目标就越模糊，反之，熵值越小，图像能量就更集中，目标也越清晰。因此，在探地雷达偏移成像中，可以应用图像熵的这个性质来优化速度模型，改善探地雷达图像的聚焦效果。

3 仿真实验

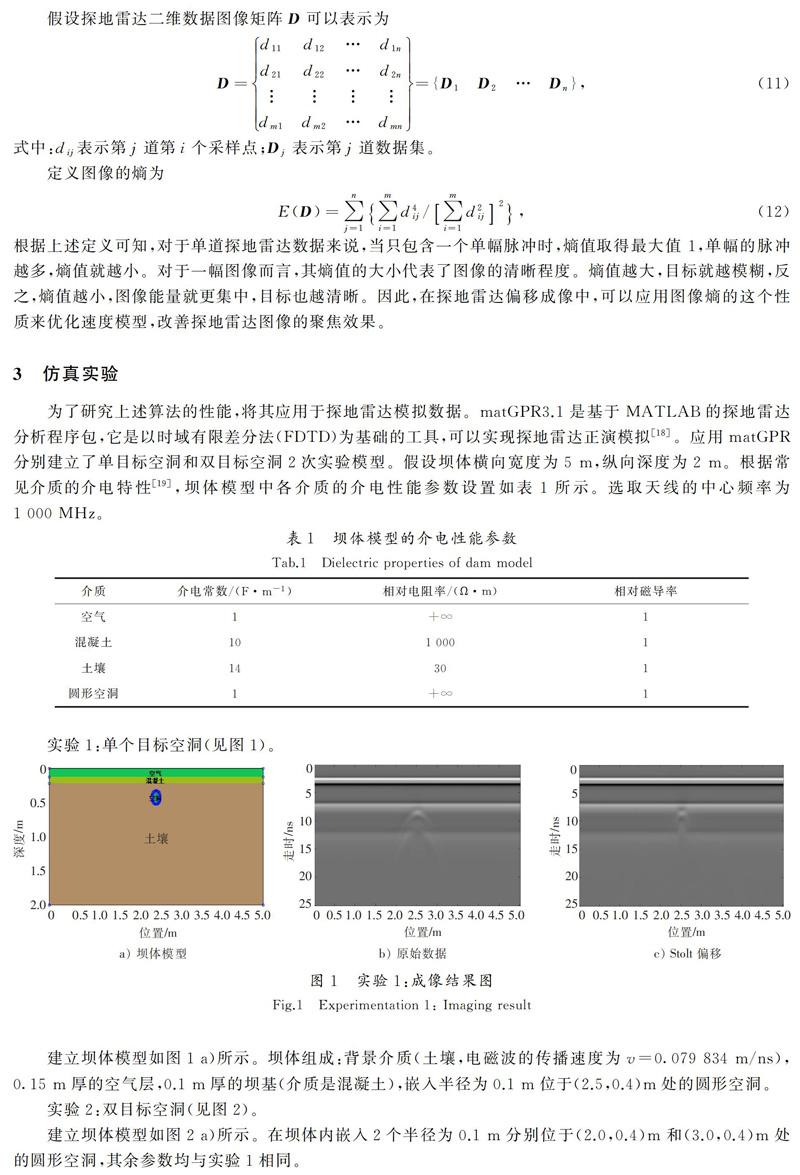
为了研究上述算法的性能，将其应用于探地雷达模拟数据。matGPR3.1是基于MATLAB的探地雷达分析程序包，它是以时域有限差分法（FDTD）为基础的工具，可以实现探地雷达正演模拟[18]。应用matGPR分别建立了单目标空洞和双目标空洞2次实验模型。假设坝体横向宽度为5 m，纵向深度为2 m。根据常见介质的介电特性[19]，坝体模型中各介质的介电性能参数设置如表1所示。选取天线的中心频率为1 000 MHz。

建立坝体模型如图1 a）所示。坝体组成：背景介质（土壤，电磁波的传播速度为v=0.079 834 m/ns），0.15 m厚的空气层，0.1 m厚的坝基（介质是混凝土），嵌入半径为0.1 m位于（2.5，0.4）m处的圆形空洞。

实验2：双目标空洞（见图2）。

建立坝体模型如图2 a）所示。在坝体内嵌入2个半径为0.1 m分别位于（2.0，0.4）m和（3.0，0.4）m处的圆形空洞，其余参数均与实验1相同。

分别对实验1和实验2坝体模型进行扫描仿真，得到原始数据图像，如图1 b）和图2 b）所示。从图中可以看出，由于坝基表面强烈的反射回波以及杂波的压制，导致目标空洞回波较微弱，不易观测空洞隐患的位置。如果直接进行Stolt偏移处理，由于目标信号是模糊的，同样也无法判断具体方位，结果如图1 c）和图2 c）所示。因此，需要对杂波进行抑制，本文采用鲁棒主成分分析算法分别对2个实验的原始数据进行处理，得到较为清晰的目标回波图像，如图3 a）和图4 a）所示。从目标回波图像中可以看出，杂波已基本得到抑制，而且没有了杂波的干扰，目標信号更易于观测。但是，目标信号的双曲线效应也显现出来。因此，再使用Stolt偏移技术进行聚焦处理，以获得较为精准的空洞位置。

本文实验1和实验2均仅选取0.065，0.070，0.075，0.080，0.085，0.090，0.095 m/ns的速度进行Stolt偏移聚焦处理，得到偏移图像，如图3 b）—h）和图4 b）—h）所示。从图3 b）和图4 b）中可以看出双曲线收敛不完全;从图3 h）和图4 h）中可以看出因过聚焦而出现拖尾上翘现象。但是仅通过肉眼不易观察出聚焦最佳的效果图像。因此，利用最小熵技术计算得到2组实验中与这些速度相对应的图像熵值分别为0.562 8，0.550 0，0.545 8，0.531 5，0.547 7，0.548 5，0.575 6和0.714 5，0.727 2，0.707 7，0.656 7，0.690 3，0.756 6，0.734 7。其2组实验的速度-熵值曲线图如图5所示。

从图5中可以看出速度为0.080 m/ns时，2组实验对应的熵值是最小的，分别为0.531 5和0.656 7，而此速度便为最优偏移速度，并且与设定的电磁波在土壤中传播的速度值最为接近，误差最小。根据此速度得到的偏移图像为图3 e）和图4 e），从图像中可以清楚地看出目标空洞的实际位置，还可以利用目标信号上下双曲线表面的时间差估计其大小。因此，在实际探测中，可以将最小熵技术用于估计电磁波在介质中的传播速度，结合Stolt偏移可以实现对目标空洞的精准定位。

4 结 语

针对使用探地雷达在水利隐患探测时得到的原始图像模糊不清而导致判断失误这一问题，提出了结合鲁棒主成分分析的Stolt偏移方法，首先利用鲁棒主成分分析算法抑制杂波改善信杂比，然后使用Stolt偏移进行聚焦处理，并结合最小熵技术估计速度有效提取到目标图像。模拟数据实验结果表明，所提方法不仅有效地抑制了坝基表面的反射回波以及杂波，而且改善了图像的分辨率，实现了对坝体内空洞的精确定位，证明了其有效性。本研究的不足之处在于Stolt偏移只适用于波速恒定的均匀介质，对于复杂的介质环境尚不能达到理想的偏移效果，之后将在算法的改进方面作进一步研究。

参考文献/References：

[1] 张伟， 李姝昱， 张诗悦， 等. 探地雷达在水利工程隐患探测中的应用[J]. 水利与建筑工程学报， 2011， 9（1）： 34-38.

ZHANG Wei， LI Shuyu， ZHANG Shiyue， et al. Application of GPR in detecting potential hazards of water conservancy projects[J]. Journal of Water Resources and Architectural Engineering， 2011， 9（1）： 34-38.

[2] 况冰. 探地雷达在水利工程隐患检测中的应用[J]. 黑龙江水利科技， 2013， 41（7）： 266-267.

[3] 张春城. 浅地层探地雷达中的信号处理技术研究[D]. 成都：电子科技大学， 2005.

ZHANG Chuncheng. Research on Signal Proeessing Technology of Shallow Subsurafce Ground Penetrating Radar [D]. Chengdu： University of Electronic Science and Technology of  China， 2005.

[4] 申家全，闫怀志，胡昌振. 基于主成分自动选择准则的探地雷达杂波抑制[J]. 电波科学学报， 2010， 25（1）： 83-87.

SHEN Jiaquan， YAN Huaizhi， HU Changzhen. Auto-selected rule on principal component analysis in ground penetrating radar signal denoising[J]. Chinese Journal of Radio Science， 2010， 25（1）： 83-87.

[5] ZHANG Yu， XIA Tian. In-wall clutter suppression based on low-rank and sparse representation for through-the-wall radar[J]. IEEE Geoscience and Remote Sensing Letters， 2016， 13（5）： 671-675.

[6] SONG Xiaoji， XIANG Deliang， ZHOU Kai， et al. Fast prescreening for GPR antipersonnel mine detection via Go decomposition [J]. IEEE Geoscience and Remote Sensing Letters， 2019， 16（1）： 15-19.

[7] 闵昆龙. 基于Stolt偏移的林木根系探地雷达SAR成像算法研究[D]. 哈尔滨：东北林业大学， 2014.

MIN Kunlong. The Study on Synthetic Aperture Imaging of Root's GPR Image Based on Stolt Migration[D]. Harbin：Northeast Forestry University， 2014.

[8] JUNG H， KANG W， KIM K. Multilayer stolt migration algorithm for subsurface target imaging in oblique layers[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing， 2017， 10（10）： 4295-4303.

[9] JUNG H， KIM K. Autofocusing technique based on generalized multilayer Stolt migration[J]. IEEE Transactions on Geoscience and Remote Sensing， 2018， 56（3）： 1386-1393.

[10]汪科. 高阶时域有限差分法的多偏移距电磁波数值成像[J]. 物探与化探， 2017， 41（3）： 489-495.

WANG Ke. High-order FDTD method for multi-offset electromagnetic numerical imaging[J]. Geophysical and Geochemical Exploration， 2017， 41（3）： 489-495.

[11]王甲勇， 肖丰霞. 克希霍夫积分偏移在探地雷达中的应用及实现[J]. 计算机应用， 2009， 29（sup2）： 385-387.

WANG Jiayong， XIAO Fengxia. Application and implementation of Kirchhoff migration integral in ground penetrating radar[J]. Journal of Computer Applications， 2009， 29（sup2）： 385-387.

[12]單刚义， 韩立国， 张丽华. 基于模型约束的Kirchhoff积分法叠前深度成像[J]. 吉林大学学报（地球科学版）， 2018， 48（2）： 379-383.

SHAN Gangyi， HAN Liguo， ZHANG Lihua. Pre-stack depth migration based on model confined Kirchhoff integration[J]. Journal of Jilin University （Earth Science Edition）， 2018， 48（2）： 379-383.

[13]修志杰， 陈洁， 方广有， 等. 基于F-K偏移及最小熵技术的探地雷达成像法[J]. 电子与信息学报， 2007， 29（4）： 827-830.

XIU Zhijie， CHEN Jie， FANG Guangyou， et al. Ground penetrating radar imaging based on F-K migration and minimum entropy method[J]. Journal of Electronic & Information Technology， 2007， 29（4）： 827-830.

[14]ZHOU Huilin， XING Wan， WEI Li， et al. Combining F-K filter with minimum entropy stolt migration algorithm for subsurface object imaging and background permittivity estimation [J]. Procedia Engineering， 2011， 23： 636-641.

[15]JAVED S， MAHMOOD A， Al-MADEED S， et al. Moving object detection in complex scene using spatiotemporal structured-sparse RPCA [J]. IEEE Transactions on Image Processing， 2019， 28（2）： 1007-1022.

[16]蔚建斌， 陈自力， 江涛. 基于偏移技术的探地雷达SAR成像方法[J]. 信号处理， 2010， 26（5）： 778-782.

WEI Jianbin， CHEN Zili， JIANG Tao. The SAR imaging method of GPR based on migration [J]. Signal Processing， 2010， 26（5）： 778-782.

[17]XU X Y， MILLER E L， RAPPAPORT C M. Minimum entropy regularization in frequency-wavenumber migration to localize subsurface objects[J]. IEEE Transactions on Geoscience and Remote Sensing， 2003， 41（8）： 1804-1812.

[18]吴学礼， 贾江波， 孟凡华， 等. 基于探地雷达的水库坝基渗漏正演模拟[J]. 河北科技大学学报， 2017， 38（4）： 389-394.

WU Xueli， JIA Jiangbo， MENG Fanhua， et al. Forward modeling of seepage of reservoir dam based on ground penetrating radar[J]. Journal of Hebei University of  Science and Technology， 2017， 38（4）： 389-394.

[19]LEGER E， DAFFLON B， SOOM F， et al. Quantification of arctic soil and permafrost properties using ground-penetrating radar and electrical resistivity tomography datasets [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2017， 10（10）： 4348-4359.