基于拓扑优化的四旋翼无人机结构设计

吉亮 丁文杰 谷春璐 李玉华 SAEED Nouman 陈卓 龙凯

摘要：为实现某四旋翼无人机的轻量化结构设计，采用Inspire进行拓扑优化设计，并对获得的拓扑优化结构进行静力分析和动力学分析。分析结果表明，通过拓扑优化方法获得的无人机结构应力分布合理，结构位移小且频率较高，满足静态和动态结构设计要求。研究结果可为实现低成本、轻量化的四旋翼无人机结构设计提供一条新的途径。

关键词：无人机; 四旋翼; 拓扑优化; Inspire

中图分类号：TH128;TB115.1

文献标志码：B

Structural design of quadrotor unmanned aerial vehicle based on topology optimization

JI Liang DING Wenjie GU Chunlu LI Yuhua SAEED Nouman CHEN Zhuo LONG Kai

（Renewable Energy School North China Electric Power University Beijing 102206 China）

Abstract：

To implement the lightweight structure design of a quadrotor unmanned aerial vehicle the topology optimization design is performed using Inspire and the static analysis and dynamic analysis of the obtained topology optimization structure are achieved. The analysis results show that stress distribution of the unmanned aerial vehicle structure derived from the topology optimization method is reasonable and the structure displacement is small and the structural frequency is high which meets the static and dynamic structure design requirements. The study results can provide an innovative way for the lowcost and light weight structure design of quadrotor unmanned aerial vehicle.

Key words：

unmanned aerial vehicle; quadrotor; topology optimization; Inspire

0 引 言

無人机广泛用于航拍、电力巡检、农业和影视拍摄等领域。四旋翼无人机以其结构相对简单、不需要反扭装置、成本低和悬停稳定等优点，得到广泛的应用。[1]目前，无人机结构设计研究大多数集中于对已有无人机结构进行刚度和强度校核，再根据分析结果反复修改结构。刘峰等[2]基于有限元法完成四旋翼无人机碳纤维结构优化设计与固有模态分析。田卫军等[3]结合振动特性设计四旋翼无人机结构。吴文志等[4]分析全力拉伸和降落工况下无人机结构的强度和刚度响应。喻辉[5]完成某重载四旋翼无人机的结构设计与强度计算。裴彦华[6]分析某多旋翼无人机结构的动态特性，同时采用拓扑优化方法对起落架连接结构进行优化。吴子毅[7]采用有限元法对惯性测量单元进行减振设计。冯琨程等[8]对某系留无人机的外壳进行自由尺寸优化。目前，有关无人机结构拓扑优化设计的系统性研究很少。

本文基于拓扑优化理论，应用商业软件Inspire，以频率为约束，对无人机进行结构拓扑优化，得到一种新型四旋翼无人机机架结构。

1 拓扑优化理论

按照层次划分，连续体结构优化分为拓扑优化、形状优化和尺寸优化3类。一般而言，形状优化和尺寸优化用于结构详细设计阶段，拓扑优化用于结构概念设计阶段。拓扑优化能够在结构初始设计阶段保证良好的传力路径，为提升结构性能和减小结构质量提供保障。[913]

现有的商业软件大多基于变密度拓扑优化方法开发。在变密度法中，材料的弹性模量与相对密度间采用假设的插值函数表示，用单元的相对密度表现材料的有无。各向同性惩罚微结构是目前应用广泛的弹性模量插值模型，其数学表达式为

式中：xi为单元i的相对密度;p为惩罚因子;Emin为相对密度为0的单元的弹性模量;E0为相对密度为1的单元的弹性模量。

为避免数值奇异性，通常取Emin=E0/109。通过引入p对中间密度单元的弹性模量进行惩罚，从而使单元的密度趋向于01分布，降低中间密度单元数量，从而获取材料清晰分布的拓扑优化结果。

在与结构频率相关的拓扑优化中，若直接采用式（1）的插值模型，会在低密度区域产生局部模态。为克服这一困难，PEDERSEN[14]在收敛判断中排除低密度区域节点自由度，提出弹性模量插值模型，即

式中：xmin为最小相对密度。

TCHERNIAK[15]提出单元质量矩阵插值模型以避免局部模态，即

式中：M*e为相对密度为1的单元质量矩阵;r为质量矩阵惩罚因子，r取6。

二者的共同点是修改低密度单元刚度与质量比值，达到避免局部模态的目的。

2 无人机结构拓扑优化

2.1 设计选型

四旋翼无人机设计要求起飞质量不小于1.6 kg。为完成起飞动作，无人机的单轴拉力F、整体结构最大质量M和载重L之间应当满足

根据经验数据，把所有电机输出动力的50%作为无人机自身平衡的动力，剩余的50%作为无人机机动飞行和抵抗风力的动力储备。[16]单个电机最大可负载质量为800 g，选择银燕XA2212KV820电机（见图1），搭配1147螺旋桨，作为无人机的动力模块，电机参数见表1。

2.2 设计区域图

根据设计要求，在Inspire中建立初始几何模型，其几何尺寸见图2。相邻电机安装座中心距为290 mm，四周高度为35 mm，中心正四边形区域为容纳电子设备的空间。

2.3 材料与属性

选用尼龙材料，其弹性模量为2.6 GPa，泊松比为0.34，密度为1.12×103 kg/m3，屈服强度为100 MPa。

2.4 优化模型与结果

考虑无人机的整体装配要求，将初始模型划分

为设计区域和非设计区域进行结构优化，机架优化

设计域模型见图3，机架总质量为805 g。电机和电机连接件质量为51 g，简化为集中质量点连接到电机座上;中心电子设备等简化为1kg质量点连接到无人机结构中心位置。

根据四旋翼无人机实际飞行时的受力情况可知，机架结构在飞行过程中受动力模块的激励。为避免飞行过程中产生共振，结构的1阶固有频率应高于电机工作频率。电机的最大工作转速为5 720 r/min，动力模块的最大激振频率为 95 Hz，故设定拓扑优化目标为结构质量最小，约束结构1阶频率大于130 Hz，其拓扑优化函数为

式中：Ne为单元总数;vi为单元i的体积;λj为结构第j阶特征值;Φj为第j阶特征值相关的特征向量;K为总刚度矩阵;M为总质量矩阵。

选择不同的最小尺寸约束进行结构拓扑优化，获得密度分布云图，见图4。采用不同的最小尺寸约束获得的拓扑构型整体上相似，翼臂类似于桁架结构，与传统的辐射状圆管翼臂结构具有较大的差别。翼臂由上、下两根较粗壮的杆和连接上、下杆的厚板构成：两根较粗壮的杆为主要的传力路径，中间厚板将上、下杆连接在一起，防止单个杆件的振动，同时提高翼臂上下振动振型和翼臂扭转振型的频率。当采用更小的最小尺寸约束时，翼臂上、下杆的连接倾向于面积更大更薄的板;当采用更大的最小尺寸约束时，获得的拓扑构型更加简洁。

a）最小尺寸约束为14 mm

b）最小尺寸约束为10 mm

c）最小尺寸约束为14 mm时的翼臂局部

3 新型机架结构分析

3.1 结构重构和静力学分析

对优化结果进行解读，机架重构对象选择约束最小尺寸为14 mm获得的拓扑构型。直接采用Inspire中的Polynurbs建模方式对优化后的机架拓扑构型进行重构。[17]重构的无人机机架结构见图5，其总质量为395 g，比最初给定的设计域总质量降低410 g。

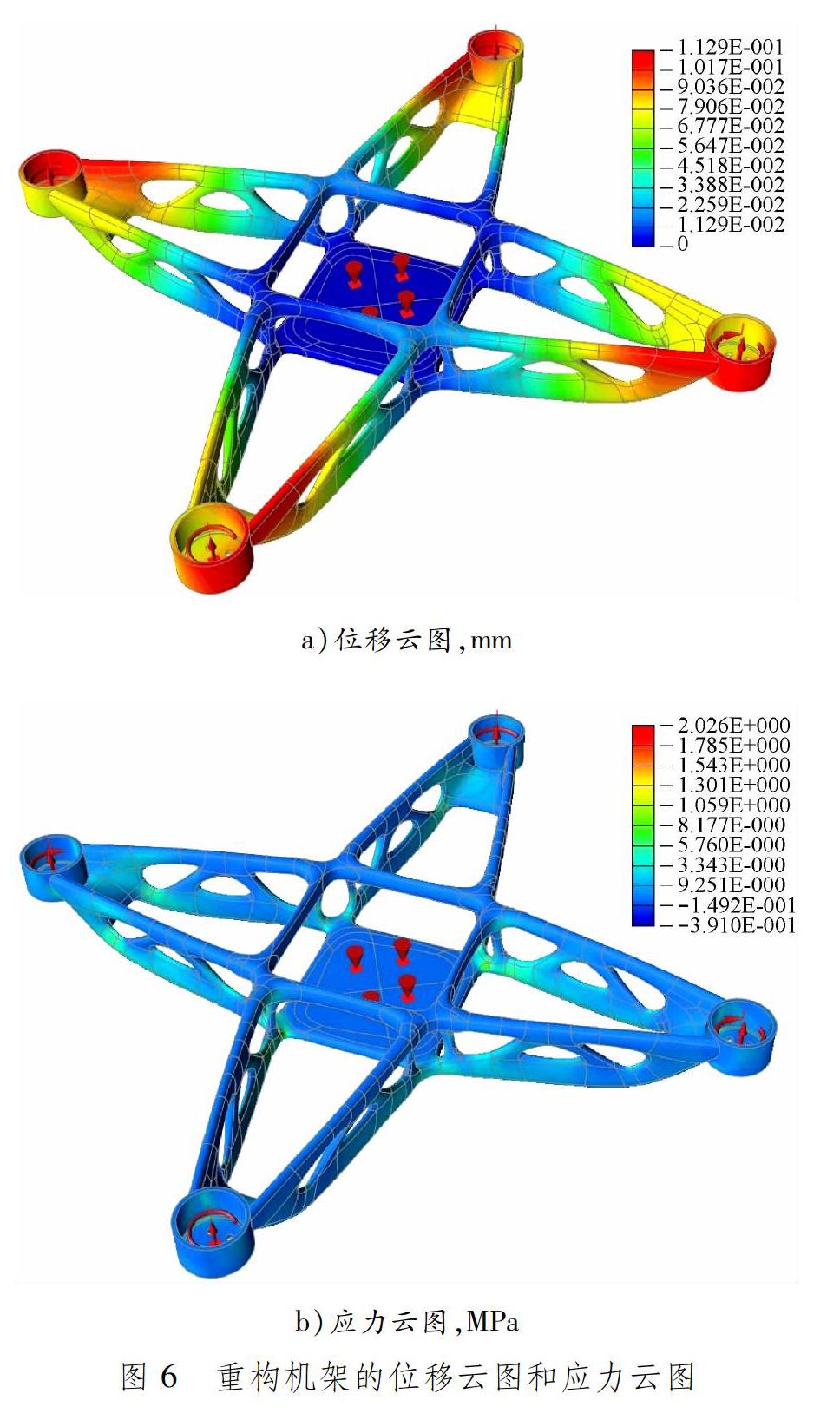
为更好地验证新型结构的合理性，在Inspire中对优化重构的无人机机架进行静力学分析。边界条件设置为每个电机座受竖直向上8.3 N的力和0.24 N·m的扭矩，固定中心部位，计算得到的位移和应力云图见图6，其最大位移为0.112 9 mm，最大应力为2.026 MPa。由此可知，结构最大位移较小，最大应力远小于材料的许用应力且分布合理，满足刚度和强度要求。

a）位移云图，mm

b）应力云图，MPa

3.2 结构动力学分析

对重构的无人机机架进行自由模态分析，校核其动力学性能。自由模态分析得到的前4阶固有频率见表2。结构的1阶频率为120.2 Hz，略低于拓扑优化中约束的130.0 Hz，但是结构1阶固有频率仍比动力模块的最大工作频率高25.0 Hz，能够有效避免共振现象发生，动力性能也能满足设计要求。重构机架的前4阶振型见图7。

无人机1阶、2阶振型为对称的2个翼臂的左右摆动，3阶振型为4个翼臂的左右摆动，4阶振型为4个翼臂的上下摆动。重构模型的频率低于约束值，一是因为在重构模型时不可能表达所有拓扑结构的细节，二是为整体结构美观，重构模型翼臂上下杆在高度方向的尺寸更大，而在左右宽度上有所降低，使得翼臂抵抗左右摆动的能力降低，即1阶频率有所降低。

5 结束语

采用拓扑优化软件Inspire，以结构1阶频率最小值为约束，以最小质量为优化目标，完成某四旋翼无人机翼臂与整体结构的同步设计。该结构与传统的四旋翼无人机结构存在较大的差别，整体结构类似桁架结构。无人机结构的静力学分析结果表明：设计的无人机结构最大位移较小，最大应力值远小于材料的许用应力值，结构的静力学性能满足要求。重构机架结构的自由模态分析结果表明：重构结构的1阶固有频率比动力模块最大工作频率高25.0 Hz，能够有效避免共振，动力性能满足要求。研究结果为四旋翼无人机机架结构的设计提供一种新的设计思路，为实现低成本、轻量化的四旋翼无人机结构设计提供一条新的途径。

参考文献：

[1] 何宇 刘海军 刘博. 微小型旋翼无人机总体设计与实现[J]. 战术导彈技术 2012（4）： 915.

[2] 刘峰 高鸿渐 喻辉 等. 基于有限元的四旋翼无人机碳纤维结构优化设计与固有模态分析[J]. 玻璃钢/复合材料 2017（4）： 1723. DOI： 10.3969/j.issn.10030999.2017.04.003.

[3] 田卫军 李郁 何扣芳 等. 四轴旋翼飞行器结构设计与模态分析[J]. 制造业自动化 2014 36（4）： 3739.

[4] 吴文志 吴斌 周星 等. 某四旋翼无人飞行器的力学仿真分析[J]. 电子机械工程 2016 32（1）： 5254.

[5] 喻辉. 重载四旋翼民用无人机设计与强度计算[D]. 广汉： 中国民用航空飞行学院 2017.

[6] 裴彦华. 多旋翼无人机动态特性分析与起落架连接件优化[D]. 长春： 中国科学院长春光学精密机械与物理研究所 2016.

[7] 吴子毅. 多旋翼无人机惯性测量单元振动分析和减振设计[D]. 长春： 中国科学院长春光学精密机械与物理研究所 2016.

[8] 冯琨程 高九州. 某型系留无人机复合材料机体结构优化设计与分析[J]. 玻璃钢/复合材料 2018（10）： 5661. DOI： 10.3969/j.issn.10030999.2018.10.009.

[9] BENDSE M P KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Applied Mechanics and Engineering 1988 71（1）： 197224. DOI： 10.1016/00457825（88）900862.

[10] BENDSE M P SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics 1999 69（9/10）： 635654. DOI： 10.1007/s004190050248.

[11] SIGMUND O MAUTE K. Topology optimization approaches[J]. Structural and Multidisciplinary Optimization 2013 48（6）： 10311055. DOI： 10.1007/s0015801309786.

[12] ANDREASSEN E CLAUSEN A SCHEVENELS M et al. Efficient topology optimization in MATLAB using 88 lines of code[J]. Structural and Multidisciplinary Optimization 2011 43（1）： 116. DOI： 10.1007/s0015801005947.

[13] THOMAS H ZHOU M SCHRAMM U. Issues of commercial optimization software development[J]. Structural and Multidisciplinary Optimization 2002 23（2）： 97110. DOI： 10.1007/s001580020170x.

[14] PEDERSEN N L. Maximization of eigenvalues using topology optimization[J]. Structural and Multidisciplinary Optimization 2000 20（1）：211. DOI： 10.1007/s001580050130.

[15] TCHERNIAK D. Topology optimization of resonating structures using SIMP method[J]. International Journal for Numerical Methods in Engineering 2002 54（11）： 16051622. DOI： 10.1002/nme.484.

[16] 高鴻渐. 微型碳纤维四旋翼无人机结构设计与优化[D]. 广汉： 中国民用航空飞行学院 2018.

[17] 徐成斌 路明村 张卫明. solidThinking Inspire优化设计基础与工程应用[M]. 北京： 机械工业出版社 2016