基于随机森林的SPS舱口盖结构性能预测

田阿利 魏震

摘要：为研究钢聚氨酯夹层板（steelpolyurethane sandwich plate SPS）舱口盖的力学性能，以结构变形和应力为设计目标，选取舱口盖7个主要设计变量，对SPS舱口盖进行静强度分析，并根据分析数据建立结构变形和应力的随机森林（random forest，RF）预测模型。预测结果表明，结构变形和应力的平均相对误差分别为3.71%和2.93%，预测精度较高，可满足工程应用。

关键词：钢聚氨酯夹层板; 舱口盖; 变形; 应力; 设计变量; 随机森林

中图分类号：U663.99;TP391.76

文献标志码：B

Structural performance prediction of SPS hatch cover based on random forest

TIAN Ali WEI Zhen

（School of Naval Architecture and Ocean Engineering Jiangsu University of Science and Technology Zhenjiang 212000 Jiansu China）

Abstract：

To study the mechanical properties of steelpolyurethane sandwich plate（SPS） hatch cover using seven main design variables of the hatch cover the static strength of SPS hatch cover is analyzed taking structural deformation and stress as design objective. The random forest（RF） forecasting model for structural deformation and stress based on analytical data is established. The prediction results show that the average relative errors of structural deformation and stress are 3.71% and 2.93% respectively. The prediction accuracy is high which can meet the engineering application.

Key words：

steelpolyurethane sandwich plate; hatch cover; deformation; stress; design variable; random forest

0 引 言

钢聚氨酯夹层板（steelpolyurethane sandwich plate SPS）结构具有轻质、高强度、耐腐蚀等优点，焊接施工量少[12]，因此使用SPS结构替代传统钢制板架形成的SPS舱口盖结构，被普遍应用于船舶制造和航空航天等领域。为研究各尺寸参数对SPS力学性能的影响并得到一定尺寸SPS舱口盖的力学性能，拟采用新型的预测方法进行分析建模。

随机森林（random forest RF）算法是一种高效的集成方法，常用于数据的回归和分类预测。[3]该方法能够在运算量变化不大的情况下有效提高模型的预测精度，对异常值和噪声具有较高的包容度，不易产生过拟合现象，且在处理大规模数据时性能表现优异，在各行各业得到广泛应用。[4]OSTMANN等[5]采用RF回归方法，对23个环境变量进行空间连续尺度上的小型底栖动物指数预测，利用RF算法可以很好地模拟物种丰富度和分类群数量的差异。DAI等[6]建立安全监测大坝的RF模型，根据袋外误差选择适当的参数并提取强解释变量，认为该模型可用于其他结构性能的分析和预测。SINGH等[7]和吴晶等[8]采用RF回归预测模型研究土壤的入滲速率，并与人工神经网络和M5P模型树技术进行比较，结果表明RF回归方法比其他2种模型效果更好。

本文针对新型SPS舱口盖结构设计，根据规范要求计算结构力学性能，并采用RF算法与有限元仿真结合的方法，建立结构变形与应力预测模型，对SPS舱口盖的应力和变形进行预测，预测结果与仿真计算结果对比验证模型的预测精度，可为舱口盖结构设计与性能预测提供参考。

1 随机森林（RF）算法

RF算法能够分析各个设计变量对因变量的影响情况。在建立决策树时，RF算法从原来的样本数据集中选取与数据样本容量相同的观测值，并且进行有放回的抽取，所以其中有些观测值会被抽取多次，有些会没有被抽取到，即为Bootstrap重新抽样方法。[9]利用Bootstrap重新抽样方法在数据集中随机抽取多个自生数据集，对样本集进行多次随机有放回取样，可得到多个Bootstrap数据集。[10]对生成的Bootstrap数据集建立相应的决策树模型，让每一棵决策树都可以完全生长、不进行剪枝，在生成决策树时保证使用变量和数据的随机化和差异化。在RF算法中，每棵决策树都在同一个数据集中独立抽取样本集，确保RF算法中的决策树具有同样的分布。[11]在分类问题中，最终的预测结果通过投票的方式产生;在回归问题中，组合多棵决策树进行预测，最终预测结果取多个决策树模型预测值的平均值。

2 随机森林（RF）模型的构建

2.1 样本数据获取

影响SPS舱口盖结构性能的因素很多，如材料属性、结构形式等，设计变量很多，模型复杂，且运算

成本大。本文主要考虑结构尺寸对SPS舱口盖的影响效果。对SPS夹层板结构性能影响较大的几何因素是上、下面板厚度和芯层厚度，对于舱口盖，强横梁和纵桁等强构件的高度对结构的变形影响也较大。保持其他条件不变，参数变量选取上层SPS的上面板厚度t11、下面板厚度t12和芯层厚度t1c，下层SPS的上面板厚度t21、下面板厚度t22和芯层厚度t2c，以及强构件高度h，建立预测SPS舱口盖结构变形和应力的RF回归模型。SPS舱口盖结构见图1。因舱口盖结构对称，且P12与P13盖板为结构最危险区域，故选择P12盖板进行有限元分析。

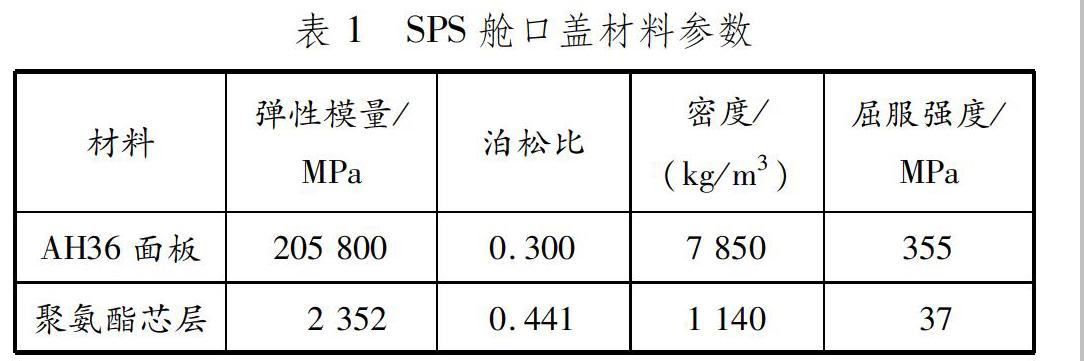
由于P12盖板两短边位于舱口围上且具有一定的限位装置，因此在短边设置简支边界条件，两长边设置为自由约束。根据《钢质海船入级规范》的要求，露天甲板舱口盖设计载荷为均布压力，大小为43.83 kN/m3，载荷施加于SPS舱口盖上面板的上表面。模型的材料参数见表1。

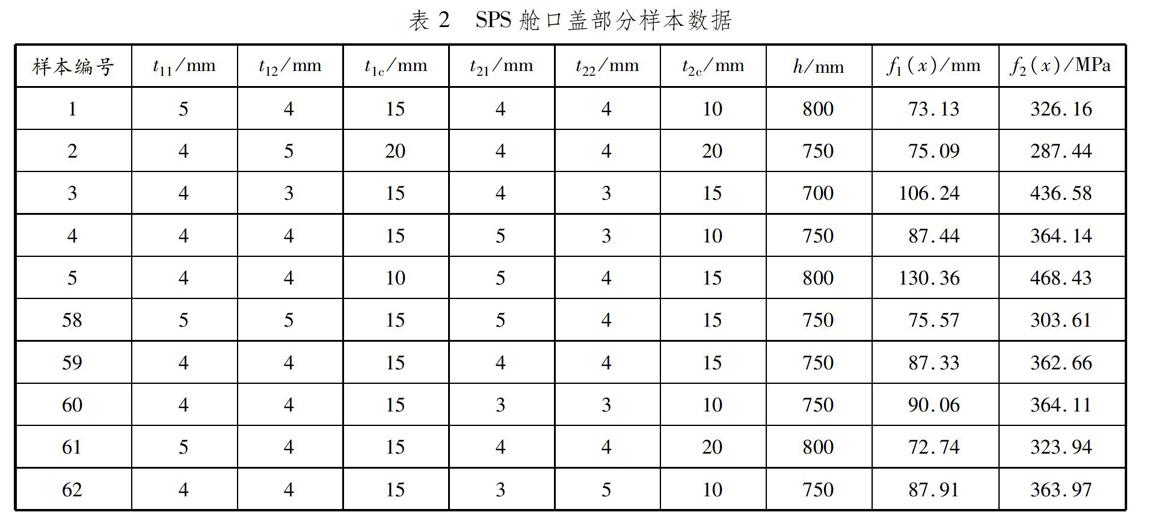
为得到试验数据，采用BoxBehnken方法对各个参数进行试验设计，充分考虑试验数据的特性，合理布置试验所需数据点在试验方案中的位置。该试验设计方法具有试验次数较少且精度较高的优点。根据各参数变量的范围，采用BoxBehnken试验设计方法选取合适的样本点，得出62组试验方案。使用ANSYS进行有限元分析计算，得到SPS舱口盖的结构变形和应力，设SPS舱口盖结构变形为f1（x）、单位为mm，结构等效应力为f2（x）、单位为MPa。以前54组试验方案数据为训练样本，后8组数据为测试样本，部分样本数据见表2。

2.2 建立RF回归模型

以f1（x）和f2（x）为因变量，影响f1（x）和f2（x）的7个参数为自变量，使用R语言构建RF回归模型[12]，将表1中f1（x）和f2（x）的训练样本数据分别保存为data_f1.csv和data_f2.csv文件。RF回归模型具有一种方便、实用的估计泛化误差的方法，即OOB袋外误差率估计方法。[13]对于每棵决策树来说，约有1/3的样本数据未参与决策树的生成，这些

样本数据称为决策树的OOB样本。通常认为特征值个数mtry最优取值为变量的平方根，决策树数目ntree通常采用网格搜索法筛选。[14]通过多次测试，当ntree设为1 000棵，在mtry=6个时，2个模型的OOB误差最小。分析不同决策树数目与OOB误差之间的关系，得到OOB误差的变化趋势见图2。2个模型的误差随ntree的增加而降低，并且逐渐达到稳定状态，说明此RF模型的泛化能力较强。

2.3 预测结果和精度

将表2中的f1（x）和f2（x）的测试数据分别存放在Newdata_f1.csv和Newdata_f2.csv文件中，使用R语言进行RF回归预测。RF算法得到的测试样本预测结果见图3，其中n为测试样本编号。为比较算法的优越性，另使用线性回归模型（linear regression model，LM）进行建模预测。由图3可知，2种不同算法均能够拟合结构变形和应力变化，RF模型预测点比LM模型更贴合实际值。f1（x）和f2（x）的预测误差见表3。由这3项误差可知，RF回归模型的预测误差均小于线性回归模型，这是因为结构参数对力学性能的影响为非线性的，不能简单使用线性模型拟合。RF模型在预测第1组数据时的误差较大，但整体误差较小。分析可知，与线性回归模型相比，RF模型能够更好地预测SPS舱口盖结构变形和应力，预测能力较好。

3 结 论

结合R语言和RF回归算法，建立SPS舱口盖结构变形和应力预测模型，并与线性回归模型进行比较。RF回归模型的拟合精度较高，结构变形和应力的平均相对误差分别为3.71%和2.93%，均方误差分别为3.43和10.45，均方根误差分别为4.54和14.57，优于传统的线性回归拟合。结构变形和应力预测与仿真值误差均较小，可为分析SPS舱口盖在各尺寸下的结构变形和应力提供参考。

参考文献：

[1] 薛启超 邹广平 何建 等. 聚氨酯弹性体隔板夹层结构的等效参数计算[J]. 复合材料学报 2017 34（3）： 564573. DOI： 10.13801/j.cnki.fhclxb.20160511.002.

[2] 周萍. 钢夹层板船体结构强度及振動性能分析[D]. 哈尔滨： 哈尔滨工程大学 2011. DOI： 10.7666/d.y2054178.

[3] 方匡南 吴见彬 朱建平 等. 随机森林方法研究综述[J]. 统计与信息论坛 2011 26（3）： 3238. DOI： 10.3969/j.issn.10073116.2011.03.006.

[4] 杨威 李维刚 赵云涛 等. 基于随机森林的钢材性能预报与影响因素筛选[J]. 钢铁 2018 53（3）： 44 49. DOI： 10.13228/j.boyuan.issn0449749x.20170427.

[5] OSTMANN A PEDRO M A. Predictive models using random forest regression for distribution patterns of meiofauna in Icelandic waters[J]. Marine Biodiversity 2018 48（10）： 714735. DOI： 10.1007/s1252601808829.

[6] DAI B GU C ZHAO E et al. Statistical model optimized random forest regression model for concrete dam deformation monitoring[J]. Structural Control and Health Monitoring 2018 25（8）： e2170. DOI： 10.1002/stc.2170.

[7] SINGH B SIHAG P SINGH K. Modeling of impact of water quality on infiltration rate of soil by random forest regression[J]. Modeling Earth Systems and Environment 2017 3（3）： 9991004. DOI： 10.1007/s4080801703473.

[8] 吴晶 陈元芳 余胜男. 基于随机森林模型的干旱预测研究[J]. 中国农村水利水电 2016（11）： 1722. DOI： 10.3969/j.issn.10072284.2016.11.005.

[9] 李欣海. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报 2013 50（4）： 11901197. DOI： 10.7679/j.issn.20951353.2013.163.

[10] 杨悦增 邓红卫 虞松涛. 基于随机森林模型的岩爆等级预测研究[J]. 矿冶工程 2017 37（4）： 2327. DOI： 10.3969/j.issn.02536099.2017.04.006.

[11] 李婉华 陈宏 郭昆 等. 基于随机森林算法的用电负荷预测研究[J]. 计算机工程与应用 2016 52（23）： 236243. DOI： 10.3778/j.issn.10028331.16060203.

[12] 陈妍 宋豫秦 王伟. 基于随机森林回归的草场植被盖度反演模型研究： 以新疆阿勒泰地区布尔津县为例[J]. 生態学报 2018 38（7）： 23842394. DOI： 10.5846/stxb201705030814.

[13] 宋康明 谭志祥 邓喀中 等. 利用随机森林回归模型预计水平移动系数[J]. 金属矿山 2016（6）： 180184. DOI： 10.3969/j.issn.10011250.2016.06.036.

[14] 宁永龙 邹蒙. 基于多元协变量和随机森林算法的宁夏用电量预测[J]. 机电信息 2019（6）： 1113. DOI： 10.19514/j.cnki.cn321628/tm.2019.06.006.