基于ANSYS Workbench的T形结构优化设计

张召颖 张帆 邹洵 张国胜 马保平

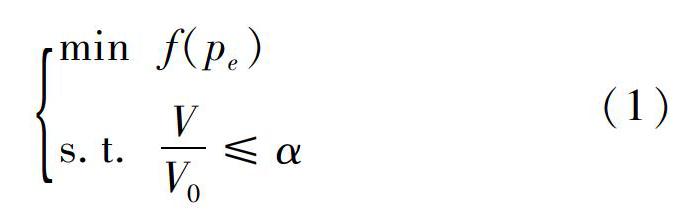
摘要：针对T形结构传统设计周期长、材料利用率低、设计成本高等问题，使用SolidWorks建立数字模型，将其转换成ANSYS Workbench可读的格式文件，进行拓扑优化设计。对T形结构在载荷作用下进行最优化设计，建立以单元材料密度为设计变量，以结构最小柔顺度为目标函数，以质量减少百分比为约束函数的数学模型。采用ANSYS Workbench的Topology Optimization模塊进行拓扑优化设计，对比优化前、后结构的应力和变形，可知运用拓扑优化技术实现T形结构的轻量化设计合理有效。

关键词：T形结构; 拓扑优化; 密度; 柔顺度; 有限元

中图分类号：TH131.9; TB115.1

文献标志码：B

Tshape structure optimization design

based on ANSYS Workbench

ZHANG Zhaoying ZHANG Fan ZOU Xun ZHANG Guosheng MA Baoping

（School of Mechanical and Automotive Engineering Shanghai University of Engineering Science Shanghai 201620 China）

Abstract：

As to the issuesthat the design cycle ofthe traditional design of Tshape structure is long the material utilization ratio is low and the design cost is high a digital model is built using SolidWorks the model is converted to the readable format file of ANSYS Workbench and the topology optimizationdesign is performed. The optimal design of Tshape structure under load is carried out. A mathematicalmodel is built in which the unit material density is design variable the minimum structural compliance is objective function and the percentage of mass reduction is constraint function. The topology optimization design is carried out using Topology Optimization module of ANSYS Workbench. The stress and deformation of optimized structure is compared with the initial one. The results show that the lightweight design of Tshape structure using topology optimization technology is reasonable and effective.

Key words：

Tshape structure; topology optimization; density; compliance; finite element

0 引 言

结构优化设计是20世纪60年代发展起来的一门新兴学科，其将数学中的最优化理论与工程设计结合[1]，运用计算机大规模处理技术，可以在众多方案中找到最优的设计方案，使结构设计使用最少的材料、采用最经济的制造方案实现结构的最佳性能。按照设计变量类型和求解问题的难易程度，优化设计可以分为3个层次：（1）尺寸优化是对某些零件的几何结构尺寸进行参数优化，比如梁的几何尺寸;（2）形状优化是优化产品的几何形状;（3）拓扑优化是在给定的设计空间内确定最优的材料分布。拓扑优化设计技术借助计算机数值仿真软件，速度快，可缩短产品的设计周期，减少企业的生产成本，降低设计研发人员的劳动强度。拓扑优化在优化设计领域是最难的，其中包括：连续体结构均匀拓扑优化方法[2]、基于均匀化方法改进的SIMP变密度法[3]等。渐进结构优化理论将变密度法0～1中的连续变量以离散的形式作为变量使用。[4]

拓扑优化技术的应用领域广泛，如航空航天、汽车和日用家电等。在市场上，有很多成熟的商业软件可以实现结构的拓扑优化设计，比如HyperWorks、SloidWorks和Nastran等。

本文基于ANSYS Workbench拓扑优化模块，对使用范围较广的T形结构进行拓扑优化设计，对比拓扑优化前、后结构的几何参数和性能参数，结果认为：在同样的边界条件下，优化后T形结构的应力和变形仍满足设计要求，质量明显减小，从而实现轻量化设计。

以“目标函数满足整体结构的柔顺度最小，约束条件满足最小柔顺度缩减结构的百分比”建立数学模型[5]，结合数值仿真分析技术优化T形结构[6]，在安全强度范围内实现减重。优化函数模型为

式中：f（pe）为目标函数;pe为第e个单元的伪密度;V为结构优化后的体积;V0为初始结构的体积;α为目标体积分数。

1 T形结构三维建模和有限元分析

1.1 T形结构三维建模

使用三维设计软件SloidWorks建立T形结构几何模型，该T形结构是一种简单结构。SloidWorks建模界面友好，与其他软件的兼容性很好。将几何模型转换为x_t格式后导入ANSYS Workbench 中进行静力学分析。该T形结构上部宽为30 mm、长为100 mm，下部结构宽为30 mm、长为120 mm，整体结构厚度为10 mm，几何尺寸示意见图1。

1.2 有限元分析

利用ANSYS Workbench，先對模型进行静力学分析，再进行拓扑优化。[79]有限元分析包括前处理和后处理2个阶段。前处理阶段包括设置材料的力学性能参数、划分网格和设置边界条件等。边界条件的设置根据真实的工况设计，将上部固定，在下部两侧施加集中载荷。软件求解后进入后处理阶段，利用软件自身提供的功能，查看载荷施加后结构的位移、应力和应变。

材料弹性模量设置为200 GPa，泊松比为0.3。前处理阶段最重要的是划分网格，网格质量好坏影响求解收敛速度和精度。从三维模型可以看出，该T形结构为薄板件，利用SloidWorks提取结构的中间面，然后进行网格划分。单元尺寸设置为2 mm，结构网格划分后共有1 781个节点和1 655个单元。T形结构网格划分结果见图2。正确设置边界条件可以使有限元模型求解收敛速度加快，结果更接近真实工况。T形结构的上部A处（T形结构上部表面）为固定约束;下部B处和C处施加竖直向下的集中载荷，大小各为10 N

。具体加载位置见图2。

求解模型得到T形结构的整体位移云图，见图3。由此可以看出：结构的最大变形为0.000 22 mm，最大变形发生在施加载荷的位置，最小变形发生在固定端的约束处。由位移云图可以看出，变形量具有对称性，符合真实工况。T形结构的等效应力云图见图4。由此可以看出：在集中载荷施加位置，T形结构应力最大;在梁的上部与下部的连接处存在应力集中现象（白色圆圈标记的区域），下部结构的左下角与右下角应力最小。存在应力集中现象，原因是上、下结构存在截面尺寸突变，符合力学变化规律。

2 拓扑优化

T形结构拓扑优化设计使用ANSYS Workbench的Topology Optimization模块，设计流程见图5。最大求解迭代次数设置为500次，收敛容差为0.1%，惩罚刚度因子为3。

T形结构上表面尺寸不变，设置为非设计区域，在求解过程中保留该区域特征。拓扑优化设计区域为结构整体，具体设置见图6。将整体结构的柔顺度最小设为目标函数，将体积函数设为约束函数，并将目标体积分数设为70%。

拓扑优化结果见图7。其中：红色区域表示要去除的部分，黄色区域表示边缘部分，灰色区域表示要保留的区域。

采用SpaceClaim进行几何处理，重建后的几何

模型见图8。将处理后的结构导入ANSYS

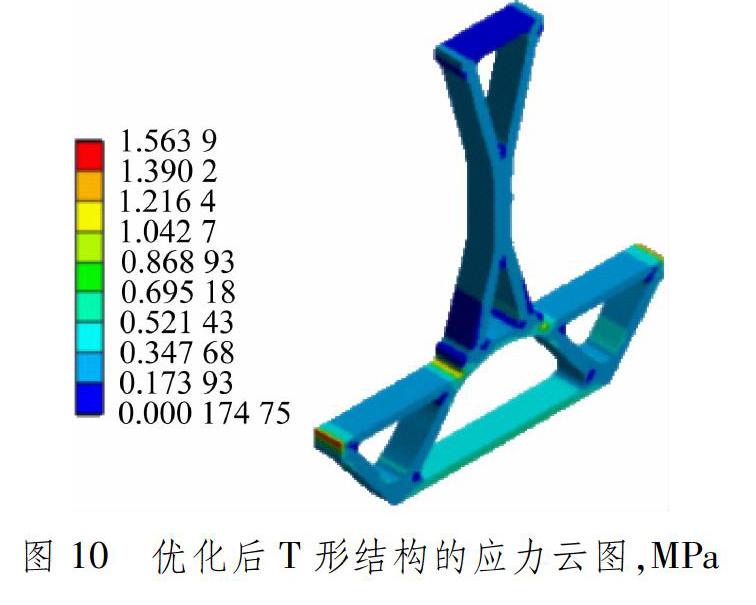
Workbench的静力学模块Static Structural中重新进行静力学分析，边界条件设置与初始模型相同：A处施加的边界条件为固定约束，B处和C处施加竖直向下10 N的载荷。优化后结构变形云图和应力云图分别见图9和10。

3 结果分析

拓扑优化前、后T形结构参数[10]对比见表1。由此可以看出：拓扑优化后T形结构的体积和质量降低69%左右;最大变形仅增加0.000 3 mm，仍在结构设计许可范围内，最大应力只增加0.02 MPa，两者均满足安全强度要求。

4 结束语

使用ANSYS Workbench中的拓扑优化模块对T形结构进行拓扑优化分析，优化后的T形结构不仅材料用量降低，而且结构受力更加均匀，符合工程实际需求。工程设计人员在产品的设计初期借助拓扑优化设计技术掌握材料的布局特点，可以大大提高设计效率。

参考文献：

[1]

谢涛 刘静 刘军考. 结构拓扑优化综述[J]. 机械工程师 2006（8）： 2225.

[2] 郭中泽 张卫红 陈裕泽. 结构拓扑优化设计综述[J]. 机械设计 2007 24（8）： 16.

[3] ROZVANY G I N ZHOU M BIRKER T. Generalized shape optimization without homogenization[J].Structural Optimization 1992 4（3/4）： 250252. DOI： 10.1007/BF01742754.

[4] XIE Y M，STEVEN G P. Evolutionary structural optimizaion[M]. Berlin： Springer Verlag 1997.

[5] 林丹益 李芳. 基于ANSYS的结构拓扑优化[J]. 机电工程 2012 29（8）： 898901. DOI： 10.3969/j.issn.10014551.2012.08.007.

[6] 范小南 文桂林. 基于Python的结构拓扑优化与3D打印试验研究[J]. 计算机仿真 2018 35（8）： 170174.

[7] 汤爱君 王红梅 李同 等. 基于ANSYS Workbench的低位缠绕机链轮支架的仿真与优化[J]. 制造业自动化 2019 41（1）： 145147.

[8] 刘韬 仲梁维 李森林. 基于ANSYS Workbench的发动机支架优化设计[J]. 农业装备与车辆工程 2018 56（11）： 7679. DOI： 10.3969/j.issn.16733142.2018.11.017.

[9] 霍洪鹏 侯晓坤 姜军生 等. 基于ANSYS拓扑优化的机器人末端结构设计[J]. 山东工业技术 2018（5）： 134135. DOI： 10.16640/j.cnki.371222/t.2018.05.117.

[10] 邢本东 王福雨 王向明. 拓扑优化在飞机舱门摇臂结构设计中的应用[J]. 计算机辅助工程 2018 27（5）： 4850. DOI： 10.13340/j.cae.2018.05.009.