不同离心力下的离心机强夯试验模拟

李玉岐 陈俊

摘要：采用PFC3D对离心机强夯试验进行数值离散模拟，在与试验对比验证模拟结果正确的基础上，研究不同离心力对数值模拟结果的影响。在30g～70g离心力下，夯沉量结果近似一致，土体的孔隙率增量、配位数和竖向峰值应力都近似相等，说明土体被夯实，符合实际情况。但是，随着离心力继续增大，即离心力在80g、90g和100g的情况下，夯锤下落时出现倾斜现象，且由于模型偏小，影响模拟数据的采集。总结认为，60g离心力为模型上限。数值模拟为研究不同离心力下的数值强夯试验提供参考。

关键词：强夯试验; 夯锤; 离心力; 夯沉量; 孔隙率; 配位数

中图分类号：TU472.31; TP391.77

文献标志码：B

Simulation of centrifuge dynamic compactiontestunder

different centrifugal force

LI Yuqi CHEN Jun

（Department of Civil Engineering Shanghai University Shanghai 200444 China）

Abstract：

The discrete numerical simulation of centrifuge dynamic compaction test is carried out using PFC3D. The simulation results are verified by the comparison with test and then the influence of different centrifugal forces on numerical simulation results is studied. When the centrifugal force is within 30g to 70g the crater depth porosity increment coordination number and vertical peak stress of soil are approximately equal. It shows that the soil is compacted which is in accordance with the actual situation. However as the centrifugal force continues to increase that is when the centrifugal force is 80g 90g and 100g the rammer inclines when it falls. Because the model is too small the collection of simulation data is affected. It is concluded that the upper centrifugal force limit of the model is 60g. The numerical simulation can provide reference for the study of numerical dynamic compaction test under different centrifuge forces.

Key words：

dynamic compaction test; rammer; centrifugal force; crater depth; porosity; coordination number

0 引 言

强夯法[13]是在20世纪60年代末70年代初由法国Menard公司首先提出的一种地基加固方法，又称为动力固结法或动力压实法。该方法将重锤提升到一定高度使其自由下落，通过夯实土层提高软土地基的承载力。[45]强夯法通常利用起吊装置，将10～40 t的重锤提升到10～40 m高度处，然后使其自由下落，夯实软土。

国内外主要有3种方法研究强夯法：室内试验、室外试验和数值模拟。OSHIMA等[6]通过室内离心机试验研究夯锤的质量、下落高度和夯击次数对加固区域和地基土体强度的影响，认为有效加固区域是由夯锤动量而非夯锤动能控制的，加固半径和加固深度与夯锤动量的对数呈线性关系。FENG等[7]对创新型锥形夯锤的底部进行强夯室内试验，认为锥形底夯锤的加固效果取决于砂土的粒度和砂颗粒的体积变化。HU等[8]通过室内试验，研究强夯加固对黄土剪切强度的影响，结果显示黄土抗剪强度随着夯击次数的增加而增大，但达到峰值后又随夯击次数的增加而减小。THILAKASIRI等[9]提出一种改进的分析方法。该方法在一系列实验室冲击试验的基础上制定，可以解决当前动态模型与软土相关的缺点。其研究结果表明，冲击应力历史和夯沉量的分析预测与试验结果一致。该研究结果有助于探索软土改良的有效强夯技术。

强夯的数值模拟主要采用有限元法或者有限差分法。PORAN等[10]最早提出一种二维有限元模型，用于模拟干砂的强夯试验，分析假设大变形公式和2种不同的弹塑性土壤模型的影响效应。GU等[11]利用有限元法分析干砂的强夯试验，使用弹塑性帽模型并假设模型的塑性行为比弹性行为作用更重要，弹性模量在多次冲击期间没有更新。虽然这个数值模型不能考虑饱和土壤中的动态固结，但其结果有利于找出强夯过程土壤的变化机理。PAN等[12]使用有限元软件Abaqus生成轴对称弹塑性土体模型模拟松土的强夯过程，并与现场试验中地面波、夯沉量和夯锤的峰值速度进行对比，结果表明该有限元模型有效。

然而，有限元法或者有限差分法都假定材料是连续体，对于某些材料来说，其本构关系不一定存在，或者说，即使这样的应力应变关系存在，也可能包含很多晦涩复杂的参数难于准确表述。对于强夯这样的大变形来说，用有限元法或者有限差分法模拟，结果可能不够理想，并且土体的細观行为难以获得，需要一种新的方法研究颗粒材料的力学行为，因此离散元法作为一种数值方法被引入。贾敏才等[13]利用PFC2D基于圆盘颗粒建立模拟砂土地基强夯加固过程的细观颗粒流模型，并与室内试验对比，验证颗粒流方法模拟强夯的可行性。MA等[14]采用PFC2D/PFC3D对块石土的强夯进行数值模拟，利用强夯过程中土体孔隙率的变化评价强夯对土体加固效果的影响，并分析颗粒的接触参数、颗粒级配和夯锤形状等对强夯效果和深度的影响。周梦佳等[15]研究颗粒形状和细粒含量对强夯效果的影响，并与现场试验进行对比。

本文基于文献[6]的离心机强夯试验，结合有关研究结果[1617]，采用PFC3D进行数值模拟，并与试验数据对比，在验证试验结果有效性的基础上，研究离心力改变对数值离心机强夯试验的影响。

1 数值模型建立

1.1 离心机强夯试验物理参数

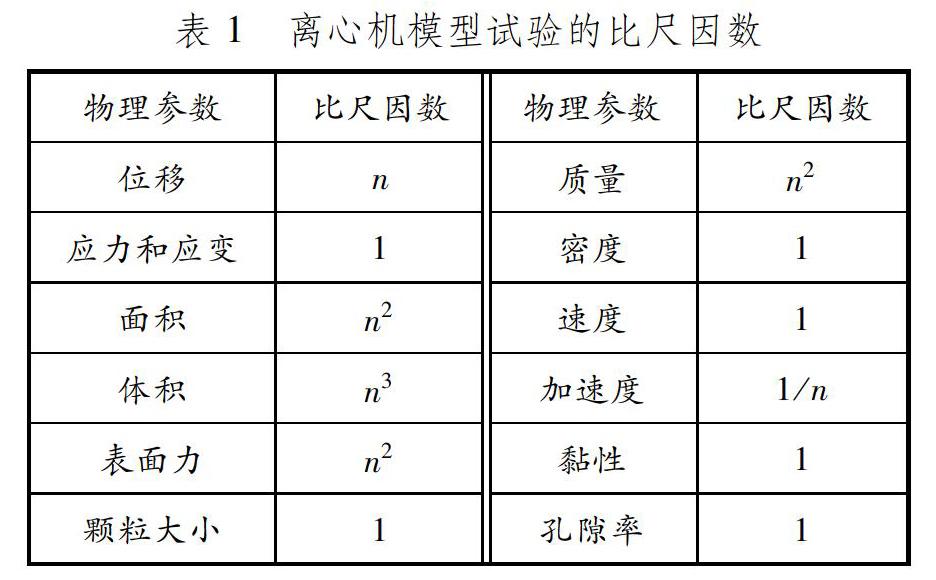
离心机模型试验的比尺因数见表1。文献[16]的离心机强夯试验示意见图1。

現场试验的地基高度为6.5 m，砂土的最大干密度和最小干密度分别为2.03和1.93 t/m3，夯锤的质量为20 t，夯锤下落高度为20 m。 为与文献中的试验结果进行对比，设定室内试验的夯锤质量为80 g，夯锤底面积为1 600 mm2，夯锤下落高度为4 380 mm;离心机的重力加速度为50g;地基采用半圆柱形模型，高度为130 mm，半径为150 mm;所用材料为干砂，孔隙比为0.44。土体颗粒的级配曲线见图2。

1.2 离心机试验模型

在PFC3D中建立模型，为减少计算量，根据对称性，采用wall命令建立1/4圆柱区域，然后在这个1/4圆柱区域内用半径扩大法建立数值模型;夯锤

采用clump命令创建;模型中不考虑粒径为0.3 mm以下的砂土，同时颗粒的粒径放大4倍。建立的离心机土体和夯锤数值模型见图3a），模型细观参数可通过三轴数值试验确定，三轴数值模型见图3b）。

最终确定的模型参数见表2。由于夯锤模型是采用clump生成的，这里给出具体夯锤的建立方法，不同离心力下的夯锤模型都按此方法生成。根据夯锤质量40 g和夯锤密度7.8 g/cm3，可确定夯锤的体积，夯锤底面积与物理试验中相同，因此可以确定夯锤的高度。在夯锤的几何尺寸确定的前提下，指

定一

定数量的小球组成夯锤，小球半径统一设置为 2

mm，

具体见图2。颗粒与颗粒之间的接触模型为滞回阻尼模型，滞回阻尼为0.75。

2 数值模拟结果分析

对于PFC3D模拟离心机强夯试验，前人已经进行研究，并给出一些分析结果[1718]，因此不再过多分析，这里仅给出夯沉量。夯沉量与夯击次数的关系见图4，图中同时给出现场试验和文献[16]室内离心机试验结果。由此可以看出，夯沉量随着夯击次数的增加而增大，且夯沉量的增加量越来越小，表明土体被夯实。

2.1 不同离心力下的数值模型

土体模型以50g离心力模型为参考，改变模型的尺寸，不改变颗粒的粒径和接触参数。50g离心力的土体数值模型尺寸为150.00 mm×130.00 mm（半径×高），相应的实际地基为7.5 m×6.5 m。同时建立离心力为30g、40g、50g和60g的数值模型。由离心机的比尺关系可以确定数值模型的参数，具体见表3。

2.2 不同离心力下的模拟结果分析

监测组成夯锤的小球位置，可以计算夯锤的竖向位移，即夯沉量。在不同离心力下，夯沉量（换算为真实尺寸）随夯击次数的变化见图5。由此可以看出，随着夯击次数的增加，整体夯沉量逐渐增大，夯沉量的增加量越来越小。4种离心力下的夯沉量趋于一致，表明离心力大小对夯沉量影响不大。

峰值应力与夯击次数的关系见图6。在整体上，随着夯击次数的增加，峰值应力逐渐增大，说明地基土体逐渐被压实。这与GU等[11]有限元法模拟强夯的峰值应力规律相同，且不同离心力下每夯的峰值应力也相近。在50g和60g离心力下，出现第5次夯击的峰值应力略小于第4次夯击的情况，有2个原因：第一，在第4次夯击完成后删除夯锤时，周围土颗粒滚入夯坑，由于50g和60g情况下夯锤的尺寸相对于土颗粒较小，因而滚入的颗粒实际上减小夯坑的高度，导致夯锤的下落速度减小，其峰值应力降低;第二，由于测量圆在50g和60g的情况下靠近模型边界，导致所测得的峰值应力数据不够稳定。

在颗粒流软件中，孔隙率表示为测量圆内空间被颗粒填充的程度。在不同离心力下6次夯击地基土体孔隙率增量对比见图7。由此可以看出，随着夯击次数的增加，土体孔隙率的增量越来越大。6次夯击后，不同离心力下土体孔隙率的增量达到0.04左右，且大致呈线性增长。从总体来看，不同离心力下土体孔隙率的增量趋于相等，表明离心力的改变对土体孔隙率的影响不明显。其中，30g离心力下的土体孔隙率增量略小于其他离心力下的土体孔隙率增量，原因是30g离心力下地基土体的初始孔隙率比其他3种离心力下的初始孔隙率小。

配位数的定义为与单个颗粒接触的周围颗粒数量，表征颗粒的紧密程度。配位数越大，颗粒接触的数目越多，模型结构越紧密。利用配位数的大小，可以分析强夯效果。在地下3.5 m处，不同离心力下土体配位数与第1夯夯击时间的关系见图8。由此可以看出：配位数总体在0.1 s左右达到峰值并随后增加，在0.6 s左右逐渐稳定;初始配位数小于稳定阶段的配位数，表明土体被夯实。在不同离心力下，配位数的变化趋势整体一致，表明在

30g～60g情况下，离心力的改变对配位数没有明显影响。

2.3 不恰当的离心力

当离心力增大时，整个模型的尺寸减小，模型中所含的颗粒数目随之减少，测量圆无法包含足够的颗粒，且夯锤容易出现倾斜现象。离心力分别为

70g、80g、90g和100g时，第6次夯击后的计算结果见图9。由此可以看出，随着离心力的增大，夯锤逐渐倾斜。这是由于颗粒相对夯锤越大，夯锤夯击后就越容易倾斜。同时，随着离心力增大，颗粒相对模型的尺寸越来越大，在这样的模型中布置测量圆，要使测量圆包含足够多的数目，测量圆的半径须相对较大。在某些情况下，第1夯过后，夯坑将出现在测量圆内，影响所测数据的准确性。因而，只有选择恰当的离心力模拟强夯试验，才可以获得更准确的细观数据。在本文中，比较6次夯击后夯锤的位置和测量圆的大小，确定60g为离心力上限。离心力越小，模型中的颗粒尺寸和数目越接近实际，模拟的结果就越理想。

3 结 论

（1） 离散元法模拟离心机强夯试验可行，模拟结果与试验结果相似。

（2） 通过改变离心力发现，在离心力为30g～60g情况下，夯沉量基本一致，同时孔隙率增量和峰值应力等都近似相等，第1次夯击后的配位数也近似相等。

（3）在70g～100g离心力情况下，模型的体积越来越小，所含颗粒数目逐渐减少，测量圆无法正确布置，夯锤逐渐出现倾斜，影响离心机强夯模拟结果。因此，建議模型的离心力最好设置在60g以下，同时模型应包含足够多的颗粒。

参考文献：

[1] 龚晓南. 地基处理手册[M]. 3版. 北京： 中国建筑工业出版社 2008： 312313.

[2] 王铁宏. 新编全国重大工程项目地基处理工程实录[M]. 北京： 中国建筑工业出版社 2004： 18.

[3] 叶书麟 韩杰 叶观宝. 地基处理与托换技术[M]. 2版. 北京： 中国建筑工业出版社 1994.

[4] 范维恒 史美筠 裘以惠. 关于强夯法加固地基的几个问题[J]. 太原工业学院学报 1982 2（2）： 1525.

[5] GAMBIN M P. Ten years of dynamic consolidation[EB/OL]. （19841231）[20190401]. https：//eurekamag.com/research/020/210/020210537.php

[6] OSHIMA A TAKADA N. Effect of tamping conditions on compaction and deformation by heavy tamping in centrifuge[DB/OL]. （2010/08/24）[20190401]. https：//www.jstage.jst.go.jp/article/jscej1984/1993/481/1993_481_135/_article/char/ja/. DOI： 10.2208/jscej.1993.481_135.

[7] FENG T W CHEN K H SU Y T et al. Laboratory investigation of efficiency of conicalbased pounders for dynamic compaction[J]. Géotechnique 2000 50（6）： 667674. DOI： 10.1680/geot.2000.50.6.667.

[8] HU R L YEUNG M R LEE C F et al. Mechanical behavior and microstructural variation of loess under dynamic compaction[J]. Engineering Geology 2001 59（3/4）： 203217. DOI： 10.1016/S00137952（00）000740.

[9] THILAKASIRI S GUNARATNE M MULLINS A G et al Investigation of impact stresses induced in laboratory dynamic compaction of soft soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics 1996 20（10）： 753767.

[10] PORAN C J RODRIGUEZ J A. Finite element analysis of impact behavior of sand[J]. Soils and Foundations 1992 32（4）： 6880. DOI： 10.3208/sandf1972.32.4_68.

[11] GU Q LEE F H. Ground response to dynamic compaction of dry sand[J]. Géotechnique 2002 52（7）： 481 493. DOI： 10.1680/geot.2002.52.7.481.

[12] PAN J L SELBY A R. Simulation of dynamic compaction of loose granular soils[J]. Advances in Engineering Software 2002 33（710）： 631640. DOI： 10.1016/s09659978（02）000674.

[13] 贾敏才 王磊 周健. 干砂强夯动力特性的细观颗粒流分析[J]. 岩土力学 2009 30（4）： 871878.

[14] MA Z Y DANG F N LIAO H J. Numerical study of dynamic compaction of gravel soil ground using discrete element method[J]. Granular Matter 2014 16（6）： 881889.

[15] 周梦佳 宋二祥. 高填方地基强夯处理的颗粒流模拟及其横观各向同性性质[J]. 清华大学学报（自然科学版） 2016 56（12）： 13121319.

[16] TAKADA N OSHIMA A. Comparison between field and centrifuge model tests of heavy test[C]// Proceedings of International Conference Centrifuge 94. Boca Raton： CRC Press 1994： 337342.

[17] LI Y Q CHEN J CHEN X H. Discrete element simulation of centrifuge test of dry sand under dynamic compaction[C]// Proceedings of GeoShanghai 2018 International Conference. Shanghai： Springer 2018： 819825. DOI： 10.1007/9789811301254_91.

[18] 陈小慧. 干砂强夯离心机试验的离散元模拟及细观特性分析[D]. 上海： 上海大学 2016.