贝叶斯统计思想在临床诊断思维训练中的应用价值

董加强 王睿 张文尧

[摘要] 临床诊断思维是在收集和分析诊断线索基础上形成诊断决策的过程。在传统的诊断学教学中往往重视诊断证据的收集，而忽视了诊断证据分析以及诊断决策形成的培训。从认知的角度讲诊断分析和决策涉及复杂的神经心理活动和经验的积累，往往具有显著的个体差异。因此，在诊断教学中加入证据分析和诊断决策形成的理论教学对于提高诊断思维培训效率具有重要意义。本文浅析贝叶斯统计思想在诊断分析和决策中的应用价值。

[关键词] 临床思维;贝叶斯定理;诊断;鉴别诊断

[中图分类号] R44;G424          [文献标识码] A          [文章编号] 1673-7210（2019）10（a）-0071-04

The application value of Bayes′ theorem in diagnostic clinical reasoning training

DONG Jiaqiang1   WANG Rui2   ZHANG Wenyao3

1.Xijing Hospital of Digestive Diseases， Air Force Medical University  State Key Laboratory of Cancer Biology， Shannxi Province， Xi′an   710032， China; 2.Department of Anesthesiology， the First Affiliated Hospital of Xi′an Jiaotong University， Shannxi Province， Xi′an   710061， China; 3.the 10th Squadron of the 3rd Brigade， School of Basic Medicine， Air Force Medical University， Shannxi Province， Xi′an   710032， China

[Abstract] Clinical diagnostic thinking is a process of making diagnostic decisions based on the collection and analysis of diagnostic clues. In the traditional teaching of diagnostics， the collection of diagnostic evidence is often emphasized， while the training of diagnostic evidence analysis and diagnosis decision-making is neglected. From the perspective of cognition， diagnostic analysis and decision-making involve complex neuropsychological activities and accumulation of experience， which often have significant individual differences. Therefore， it is of great significance to add the theory teaching of evidence analysis and diagnosis decision formation in diagnosis teaching to improve the training efficiency of diagnosis thinking. This paper analyzes the application value of bayesian statistics in diagnosis analysis and decision making.

[Key words] Clinical reasoning; Bayes theorem; Diagnosis; Differential diagnosis

臨床诊断思维是医生在收集疾病信息基础上通过综合分析确立临床诊断的思维过程。临床诊断思维的培训贯穿整个医疗执业生涯，其养成一定程度上依赖老师、前辈的言传身教，但更多的是在临床实践中的总结和领悟，是基于临床经验形成的直觉性思维，往往具有“只可意会，不可言传”的神秘色彩，导致临床思维的养成过程存在显著的个体差异。因此，将临床思维的培训从“经验”“直觉”上升到“理论”层面有利于提高医生，特别是医学生临床思维养成的效率。贝叶斯统计思想在涉及分析与决策的众多领域应用广泛[1-3]，在临床科研中也得到越来越多的应用[4-7]，但在临床教学中的应用研究仍有待深入[8]。

1 贝叶斯定理简述

贝叶斯定理是英国业余数学家Thomas Bayes于18世纪提出的用于计算“逆向概率”或称为“后验概率”的统计学思想，表述为P（A│B）=■，其中P（A│B）表示事件B发生时事件A发生的概率，P（A）表示事件A发生的概率，P（B│A）表示事件A发生时事件B发生的概率，P（B）表示事件B发生的概率，该公式可由P（A∩B）=P（A）×P（B│A）=P（B）×P（A│B）推导而来，即事件A、B同时发生的概率等于事件A发生的概率乘以事件A发生时事件B发生的概率，等于事件B发生的概率乘以事件B发生时事件A发生的概率[9]。P（A）和P（B）也通常被称为事件的“先验概率”，P（A│B）和P（B│A）则被称为事件的“后验概率”。

医学理论教学是将疾病特点分解的过程，讲述某种疾病表现为特定症状、体征、阳性辅助检查的“正向概率”或者“先验概率”，例如Ⅳ期结肠癌患者血清中癌胚抗原（CEA）升高的概率是65%。而临床诊断决策则是根据患者症状、体征和辅助检查结果反向推理，根据“反向概率”或者“后验概率”大小确定诊断，例如，患者体检发现血清CEA升高，医生要通过这一指标推测患者患结肠癌的概率大小。

2 诊断依据与诊断的区别

根据贝叶斯理论，症状、体征、辅助检查结果均可被定义为“检验（Test）”，而是否患病则被定义为“事件（Event）”。从某种程度上讲没有完美的“检验”，即任何检验均有可能得出“假阳性”或者“假阴性”的结果，也就是说几乎不存在“灵敏度”和“特异性”均為100%的“检验”[10]。因此，“检验”≠“事件”，从临床诊断思维的角度讲就是“诊断证据”≠“诊断”，例如“血清CEA升高”是一个“检验”，而“结肠癌”是一个“事件”，血清CEA升高可以为结肠癌提供诊断依据，但血清CEA升高并不意味着可以下结肠癌的诊断。贝叶斯理论就是通过对“检验”的“错误”（假阳性或者假阴性结果）进行校正，从而将“检验”的灵敏度和特异性转化为“事件”发生的概率。初接触临床的医生往往容易犯根据某一结果阳性而片面诊断某一疾病的错误，其本质就是没有分清“诊断依据”和“诊断”的区别。

在临床实践中有些“检验”可以作为诊断的“金标准”，“金标准”的特征是什么呢？贝叶斯公式可展开为P（A│B）=■=■，此公式分母中P（■）表示事件A不发生的概率，P（B│■）表示事件A不发生时事件B发生的概率，即事件B发生的概率等于事件A发生时事件B发生的概率与事件A不发生时事件B发生的概率之和。由此公式可推导当P（■）×P（B│■）=0时P（A│B）=1。P（■）×P（B│■）=0意味着“检验B”的假阳性率为0，即“检验B”的特异性为100%。因此，严格意义上讲只有特异性为100%的“检验”可以作为诊断“金标准”。同理可得只有灵敏度为100%的“检验”可以作为排除诊断的“金标准”。

3 流行病学：先验概率的重要来源

贝叶斯公式可以写成P（A│B）=P（A）×■，如前所述 P（A）为事件A的先验概率，P（A│B）为事件A的后验概率，■则可以理解为事件B对事件A先验概率的“校正系数”。流行病学资料提供疾病在人群中患病的基线数据，是疾病先验概率的重要来源。然而，流行病学资料的重要性在临床教学和实践中往往被忽视，但流行病学资料提供的疾病基础发病率的高低却是“先考虑常见多发病，后考虑少见罕见病”临床诊断思维的基础[11]。

以结直肠癌为例，其在不同的性别和年龄段发病率存在显著差异，表1为2015年中国癌症统计中发表的结直肠癌在不同年龄段不同性别人群中的发病率[12]。粪便免疫化学（fecal immunochemical test，FIT）是结直肠癌筛查最为普遍和简易的筛查方法，综合大样本的研究FIT对结直肠癌预测的灵敏度为0.73，特异性为0.95[13]。由表1可知<30岁的女性结直肠癌年发病率为1.1‰，而60～<75岁的男性结直肠癌年发病率可达90.9‰。假如一个20岁的年轻女性（YF）和一个70岁老年男性（OM）在体检中发现FIT阳性，由贝叶斯公式计算可知两者患结直肠癌的概率分别为：

P（YF│FIT）=■=0.016

P（OM│FIT）=■=0.579

前者患结直肠癌的可能性非常低，而后者接近60%的可能性为结直肠癌，这就从理论上解释了为何对于老年FIT阳性患者要高度怀疑结直肠癌，而在年轻患者中则要考虑排除其他疾病。

表1   2015年中国结直肠癌发病率统计结果（‰）

4 鉴别诊断：后验概率的比较

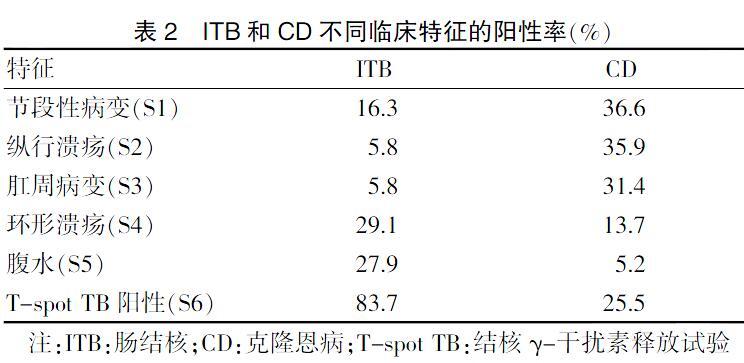
鉴别诊断是通过临床表现、辅助检查结果推断不同疾病患病可能性大小的过程，其本质是比较患不同疾病后验概率的大小。以肠结核（ITB）和克隆恩病（CD）的鉴别诊断为例：当肠道病变呈节段性，溃疡为纵行溃疡，伴有肛周病变时，临床上倾向于诊断CD;当肠道溃疡呈环形，伴有腹水，结核γ-干扰素释放试验（T-spot TB）阳性，临床上则倾向诊断ITB[14]。通过贝叶斯定理计算后验概率可以对上述诊断倾向从理论上得到解释。

回顾文献可知初诊疑似ITB和CD的患者最终确诊为ITB和CD的比例约为36%和64%。表2为不同症状、体征和辅助检查在ITB和CD中的阳性率。

此时涉及多个不同的“检验”，其贝叶斯后验概率可通过下述公式计算：

P（Ei│S1，S2，……Sr）=

■，i=1，2，3，..， k[15]。该公式中E1，E2，E3，…Ek表示不同事件发生的先验概率，在临床诊断中可以理解为不同的疾病如CD，ITB等的基础发病率;S1，S2，S3，…，Sr表示不同“检验”的阳性概率，在临床诊断中可以理解为不同症状、体征、辅助检查在某一特定疾病中出现的阳性率。

根据上述公式计算节段性病变、纵行溃疡、肛周病变患者患ITB和CD的概率分别为：

P（ITB│S1，S2，S3）=

■=

0.007，

P（CD│S1，S2，S3）=

■=

0.993。

可见根据节段性病变、纵行溃疡和肛周病变计算所得CD后验概率显著高于ITB后验概率。

同理，根据上述公式计算环形溃疡、结核病史和T-spot TB阳性患者ITB和CD的概率分别为：

P（ITB│S4，S5，S6）=

■=

0.954，

P（CD│S4，S5，S6）=

■=

0.045。

可见根据环形溃疡、腹水和T-spot TB阳性计算所得ITB后验概率显著高于CD后验概率。

5 综合诊断的理论基础

结合临床症状、体征及辅助检查“综合分析”是临床诊断思维的要点之一，其理论基础仍可通过贝叶斯理论获得解释。首先，支持证据越多诊断越可靠。以上述ITB与CD鉴别诊断为例：当影像学资料发现肠道节段性病变时，诊断为CD的概率为P（CD│S1）=■=0.80，如在此基础上肠镜检查发现肠道纵行溃疡，诊断CD的概率则从0.80提高到P（CD│S1，S2）=■=0.96。以此类推，支持诊断的证据越多，诊断的可靠程度越大。同样，不支持的证据也可以降低诊断的可靠性。如上述患者在影像和肠镜检查的基础上查体发现存在腹水，则此时诊断CD的概率会从0.96下降至P（CD│S1，S2，S6）=

■=

0.82，如同时发现T-spot TB阳性，则诊断CD的概率会进一步下降至P（CD│S1，S2，S5，S6）=

■=

0.58。

6 遗传咨询的正确解读

随诊基因检测技术的飞速发展和精准医学时代的到来，疾病遗传风险分析越来越受重视。理论上讲遗传风险的分析和解读应由受过专业训练并获得职业资格的遗传咨询师完成，然而我国目前遗传咨询行业尚处于起步阶段，遗传咨询师岗位空缺严重，从而导致临床医生成为潜在的咨询对象。因此，掌握遗传咨询的相关理论和方法可能是未来临床医生应具备的基本技能之一。

遗传风险评估从本质上讲其基本原理仍是贝叶斯统计思想，是结合家族史的“后验概率”计算的过程[16]。以林奇综合征为例，该病系由于染色体错配修复（MMR）基因胚系缺陷导致的常染色体显性遗传病，与结肠癌、子宫内膜癌等恶性肿瘤的发生密切相關[17-19]。MMR基因包括MLH1、MSH2、MSH6、MSH3、PMS1以及PMS2等，其中以MSH2表达缺失最为常见[20]。假如一名40岁男性进行了一项灵敏度和特异性均为99%的基因检测发现MSH2表达缺失，那么该男性患林奇综合征的概率究竟有多高呢？由表1数据可知该年龄段男性结直肠癌的发病率为1.3‰，在所有结直肠癌患者中约3%为林奇综合征所致，因此林奇综合征在该年龄段男性中先验概率约为0.004%。如该男性直系亲属中无早发结直肠癌等家族史，根据贝叶斯公式计算其林奇综合征的概率为■=0.004，患林奇综合征的可能性极低。如该男性父母亲有早发结直肠癌或者母亲有子宫内膜癌等恶性肿瘤病史，应推荐在相应的肿瘤标本中检测MSH2的表达，如证实MSH2表达缺失，根据常染色体显性遗传规律该男性林奇综合征的先验概率升高至50%，此时根据贝叶斯公式计算的林奇综合征后验概率升至■=0.99，该患者极有可能患有林奇综合征，应推荐其定期行结肠镜检查监测结直肠癌的发生。

可见结合家族史和基因检测结果综合计算遗传风险“后验概率”是形成正确遗传咨询结论的思维基础，是避免基因检测带来不必要恐慌，同时也不漏诊高遗传风险个体的关键。

7 总结

从认知角度讲临床诊断思维的形成是一个复杂的过程，是直觉与理性分析综合作用的结果。关于诊断思维的形成过程主流观点分为两派，即“假说-演绎法”和“经验-分析法”，前者是医学初级从业者常采用的方法，而后者多为经验丰富的医务工作者所采用[21-22]。但是，从某种程度上上述两类方法都涉及对初始“假说”或“诊断”的修正从而确立最终诊断。而修正的过程就是对不同疾病可能性的计算和筛选，本质上就是对贝叶斯定理自觉不自觉的实践[23]。

临床实践是讲究时效性的复杂的实践活动，很难要求所有的诊断都按部就班的去对比不同疾病的概率。本文的目的在于为刚接触临床的见实习生、规培生和低年资住院医师培养诊断思维提供一种工具和理论方法，提高诊断思维的养成效率和质量。

[参考文献]

[1]  浮豪豪，杨刘刘.基于贝叶斯定理的能源供应网络脆弱性研究[J].统计与决策，2019（16）：35-39.

[2]  邓世广，周龙泉，马亚伟，等.基于贝叶斯定理的地震危险性概率预测研究[J].中国地震，2019，35（1）：1-13.

[3]  孙惠丽，陈维华，刘东朝.基于深度学习的改进贝叶斯网络入侵检测算法[J].软件工程，2019，22（4）：17-20，16.

[4]  杨洋，黄启云，刘追星.基于贝叶斯网络之胃癌的辨证标准研究[J].陕西中医药大学学报，2019，42（2）：119-126.

[5]  黄孟欣，胡玲，张云展，等.中药注射剂联合FOLFOX4化疗方案治疗胃癌的贝叶斯网状Meta分析[J].中药药理与临床 2019，35（1）：160-164.

[6]  张飞飞，周涛，陆惠玲，等.基于贝叶斯粗糙集的肺部肿瘤CT图像高维特征选择算法[J].生物医学工程研究，2018， 37（4）：404-409.

[7]  罗文舒，胡湘，杨卓欣，等.基于MATLAB中风病常用中成药适宜人群的朴素贝叶斯分类器构建[J].山西中医 2018， 34（7）：51-53.

[8]  汤毕书.浅谈贝叶斯定理在疾病诊断中的应用[J].科技与创新，2019（1）：152-153.

[9]  Jaynes ET. Probability theory：the logic of science [M]. 3 edn. New York，NY：Cambridge Press;2003.

[10]  Kent P，Hancock MJ. Interpretation of dichotomous outcomes：sensitivity，specificity，likelihood ratios，and pre-test and post-test probability [J]. J Physiother，2016，62（4）：231-233.

[11]  Ashby D，Smith AF. Evidence-based medicine as Bayesian decision-making [J]. Stat Med，2000，19（23）：3291-3305.

[12]  Chen W，Zheng R，Baade PD，et al. Cancer statistics in China，2015 [J]. CA Cancer J Clin，2016，66（2）：115-132.

[13]  Song LL，Li YM. Current noninvasive tests for colorectal cancer screening：An overview of colorectal cancer screening tests [J]. World J Gastrointest Oncol，2016，8（11）：793-800.

[14]  Kedia S，Das P，Madhusudhan KS，et al. Differentiating Crohn′s disease from intestinal tuberculosis [J]. World J Gastroenterol，2019，25（4）：418-432.

[15]  Hall GH. The clinical application of Bayes' theorem [J]. Lancet 1967，2（7515）：555-557.

[16]  Hampel H. Genetic counseling and cascade genetic testing in Lynch syndrome [J]. Fam Cancer，2016，15（3）：423-427.

[17]  Sinicrope FA. Lynch Syndrome-Associated Colorectal Cancer [J]. N Engl J Med 2018，379（8）：764-773.

[18]  Singh S，Resnick KE. Lynch Syndrome and Endometrial Cancer [J]. South Med J，2017，110（4）：265-269.

[19]  Lynch HT，Snyder CL，Shaw TG，et al. Milestones of Lynch syndrome：1895-2015 [J]. Nat Rev Cancer，2015，15（3）：181-194.

[20]  Usha L，Dewdney SB，Buckingham LE. Tumor Screening and DNA Testing in the Diagnosis of Lynch Syndrome [J]. JAMA，2016，316（1）：93-94.

[21]  Elstein AS，Schwartz A. Clinical problem solving and diagnostic decision making：selective review of the cognitive literature [J]. BMJ，2002，324（7339）：729-732.

[22]  Herrle SR，Corbett EC Jr，Fagan MJ，et al. Bayes′ theorem and the physical examination：probability assessment and diagnostic decision making [J]. Acad Med，2011，86（5）：618-627.

[23]  Gill CJ，Sabin L，Schmid CH. Why clinicians are natural bayesians [J]. BMJ，2005，330（7499）：1080-1083.

（收稿日期：2019-05-10  本文編辑：封   华）