脉冲型地震下地震动强度指标与基础隔震结构位移响应相关性研究

王亚楠，于 娇，杜永峰

(1.西安工业大学 建筑工程学院，西安 710021；2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

与普通强地震动相比，近断层脉冲型地震动的特点非常明显，由于其在短时间内会对结构产生很高的能量输入，故这类地震动对结构物的潜在破坏力也更大[1-4]。隔震技术作为一种有效的控震技术，近年来已经越来越多地应用于实际工程，那么隔震结构在近断层脉冲型地震动作用下的抗震性能如何自然而然地引起了国内外研究者的重视[5-12]。地震动强度指标的筛选作为结构抗震性能研究工作的重要组成部分近年来备受关注，国内外相关研究者针对地震动强度指标与结构地震响应之间的关系进行了较深入的研究[13-20]。

对现有研究成果进行总结可以看出，结构类型不同、地震动特性不同，适用于结构抗震性能研究的地震动强度指标也不同，故应视具体情况进行专门研究。文中以隔震结构等效单自由度(Single Degree of Freedom,SDOF)体系为研究对象，以近断层脉冲型地震记录为输入，对不同地震动强度指标与等效SDOF体系脉冲型地震位移响应的相关性进行了统计研究，并分别以一榀5层和8层隔震框架为例，对分析结果进行了算例验证。

1 脉冲型地震记录的选取

从美国太平洋地震工程研究中心(PEER)强震记录数据库中选取部分近断层脉冲型地震记录，选取准则详见文献[12]，所选地震记录如表1所示。

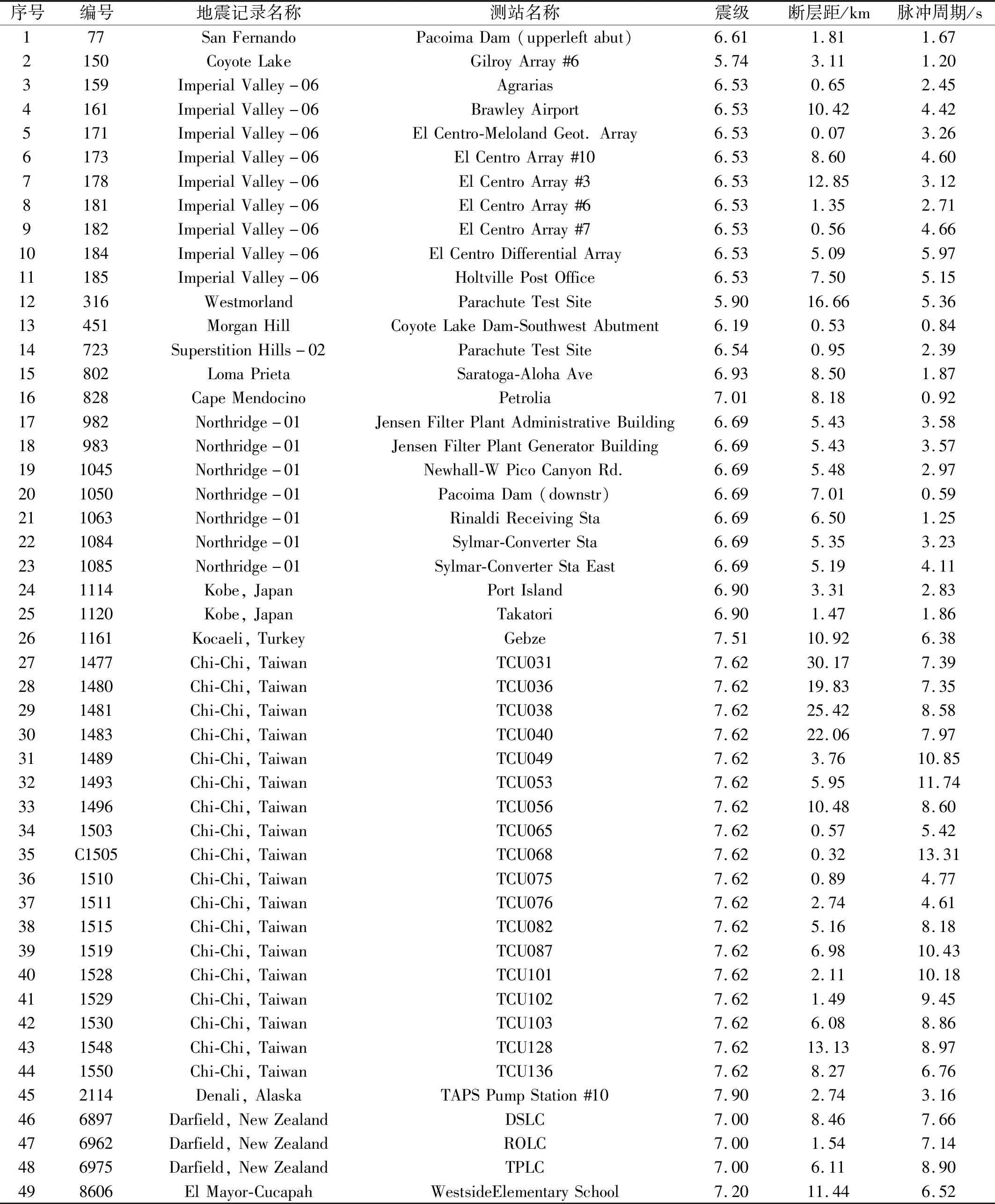
表1 近断层脉冲型地震记录Tab.1 Nearfault pulse-like ground motion records

2 等效SDOF体系及运动方程

以铅芯橡胶支座(Lead Rubber Bearing,LRB)多层基础隔震结构为例，考虑到该类结构在普通地震动作用下的运动特征，将其简化为SDOF体系进行相关性研究，非线性力-变形关系与隔震层一致。

地震作用下隔震等效SDOF体系的运动方程可写为

(1)

等效SODF体系的恢复力用隔震层恢复力来代替，是隔震层所有支座恢复力累加的结果。LRB隔震支座的恢复力采用Bouc-Wen模型进行描述，其数学表达式为

Fb=αk1xb+(1-α)FyZ

(2)

式中：k1为隔震支座屈服前刚度；α为隔震支座屈服后与屈服前的刚度比；xb为隔震支座的相对位移;Fy为支座屈服力；Z为考虑材料滞回特性的无量纲分量，其表达式为

(3)

式中：xy为支座屈服位移；A,β，γ，η为控制滞回环形状的无量纲参数，一般通过实验确定。

将式(2)代入式(1)，联立式(1)和式(3)可得

(4)

采用四阶龙格库塔法对式(4)进行求解，即可得到体系的非线性地震响应。

表2所列为利用式(4)求解SDOF体系地震响应时相关参数的取值，表2中屈重比SR在给定周期T1和屈服位移xy基础上通过计算得到，其余参数来源于隔震支座生产厂，分析时可参考文献[21]进行取值。

表2 等效SDOF体系参数取值Tab.2 Parameter values of the equivalent SDOF system

3 相关性分析

3.1 地震动强度指标选取

表3所列为文中选取的13个地震动强度指标，包括加速度型、速度型、位移型和其它指标。下文将研究这些地震动强度指标与等效SDOF体系脉冲型地震位移响应之间的相关性。

表3 地震动强度指标Tab.3 Seismic ground motion intensity measures

3.2 相关性统计分析

常用相关性统计分析方法有两种，Pearson相关系数法和Spearman秩相关系数法，其中，Pearson相关系数法在进行统计分析时要求成对存在的两连续变量数据所来自的总体是服从正态分布或接近正态的单峰对称分布，并且数据至少在逻辑范围内必须是等间距的。考虑到文中双变量的分布特征和间距等因素的影响，采用Spearman秩相关系数rs来评价地震动强度指标与隔震结构脉冲型地震位移响应之间的相关性，|rs|值越大，说明相关性越好。具体步骤如下：

步骤1体系自振周期的取值范围为0.2～3.0 s，间隔0.2 s，阻尼比取0.05。

步骤2依次计算与每一条地震记录对应的各地震动强度指标和该地震记录作用下体系的最大位移响应。

步骤3采用Spearman方法统计得到各地震动强度指标与体系最大位移响应之间的秩相关系数值rs。

Spearman秩相关系数rs为一个与分布无关的统计参数，适于一般的双变量相关性分析，它的取值范围为[-1,1]，其绝对值越接近1，表明两个变量之间的相关程度越高。一般根据|rs|的取值大小，将相关程度分为3个等级，0<|rs|≤0.3表示相关程度较低，0.3<|rs|≤0.6表示相关程度显著，0.6<|rs|≤1表示相关程度很高[22]。rs的数学表达式为

(5)

式中:di=rg(Xi)-rg(Yi)为双变量秩的差；n为统计变量的数量。

图1所示为近断层脉冲型地震记录作用下，地震动强度指标ASI与不同T1的等效SDOF体系位移响应之间的相关性分析结果。从其散点分布图与相关性系数rs之间的对应关系可以看出，采用Spearman方法对相关性进行统计研究是合理的。

表4所列为不同地震动强度指标与隔震等效SDOF体系最大位移响应之间的|rs|值。以|rs|≥0.6作为判别地震动强度指标是否适用的界限值，从表4可知，除CAV外的加速度型指标适于0.2 s≤T1≤0.8 s的短周期隔震结构；速度型指标分为两类，其中，VSI和HI适于0.2 s≤T1≤1.4 s的短、中周期隔震结构，PGV和Vrms适于0.2 s≤T1≤2.6 s的短、中、长周期隔震结构；位移型指标适于1.6 s≤T1≤3.0 s的中、长周期隔震结构；其它指标V/A适于2.0 s≤T1≤3.0 s的长周期隔震结构。由于CAV对应|rs|均小于0.6，故将其淘汰。

图1 ASI与最大位移响应之间的相关性Fig.1 Correlation between the maximum displacement response and ASI

表4 相关系数绝对值Tab.4 Absolute value of correlation coefficients

图2所示为各地震动强度指标(除CAV外)对应相关系数|rs|与周期T1的关系曲线，以下简称“相关系数曲线”。从图2可知，相关系数曲线的分类化特征明显，根据其变化趋势可分为3类。其中，第1类曲线簇由加速度型指标(PGA，Ia，Arms，Ic和ASI)和速度型指标(HI和VSI)对应的相关系数曲线组成，适于0.2 s≤T1≤0.8 s的隔震结构；第2类曲线簇由速度型指标(PGV和Vrms)对应的相关系数曲线组成，适于0.8 s

4 算例验证

利用SeismoStruct分别建立5层和8层基础隔震结构的非线性数值计算模型。其中，5层基础隔震结构的屈前周期T1为0.655 s，8层基础隔震结构的屈前周期T1为0.879 s。以表1所列脉冲型地震记录为输入进行动力时程分析，采用Spearman方法分别对隔震层最大变形和上部结构最大层间位移与地震动强度指标的相关性进行统计研究，对上文基于等效SDOF体系所得研究结果的适用性和有效性进行验证。

图3所示分别为5层和8层隔震结构的相关性分析结果。从图3可知，二者与地震动强度指标的相关性从趋势上看几乎一致，即与加速度型指标和速度型指标相比，位移型指标和其它指标与结构位移响应的相关性最差，速度型指标中VSI和HI与结构位移响应的相关性最好；经对比建议选取VSI或HI作为多层隔震结构地震位移响应预测等相关研究的优选地震动强度指标。

图4所示分别为5层和8层隔震结构相关性分析结果与上文基于等效SDOF体系相关性分析结果之间的对比。从图4中可知，隔震结构与其等效SDOF体系之间的相关系数曲线趋势一致，相关系数取值非常接近，说明以隔震等效SDOF体系为研究对象优选得到的地震动强度指标对于多层基础隔震结构具有较好的适用性和有效性。

图3 隔震结构位移响应与地震动强度指标间的相关性分析Fig.3 Correlation analysis between displacement responses of base-isolated structure and ground motion intensity measures

图4 隔震结构与其等效SDOF体系的相关性分析结果对比Fig.4 Comparison of correlation analysis results between base-isolated structure and its equivalent SDOF system

5 结 论

文中对近断层脉冲型地震动作用下常用地震动强度指标与基础隔震结构位移响应之间的相关性进行了研究，主要得到如下结论：

(1)与加速度型、位移型和其它指标V/A相比，速度型指标在短、中、长周期范围内均与隔震等效SDOF体系地震位移响应呈现出较高的相关性，适用范围相对更广。

(2)各地震动强度指标对应相关系数曲线的分类化特征明显，据其变化趋势可分为3类；其中对应第1类曲线的地震动强度指标更适于多层基础隔震结构。

(3)以隔震等效SDOF体系为研究对象优选得到的地震动强度指标对多层基础隔震结构具有较好的适用性和有效性，建议将VSI或HI作为优选指标进行多层基础隔震结构地震位移响应预测等相关方面研究。