基于参数优化时变滤波经验模态分解的转子故障诊断

唐贵基，周 翀，庞 彬，李楠楠

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

Keywords:rotor;fault diagnosis;time-varying filtering;empirical mode decomposition;parameter optimization;Hilbert transform(HT)

如何提取出转子不平衡、碰磨、油膜涡动、裂纹等典型非线性、非平稳故障信号的故障特征，以准确诊断出转子故障类型，是转子系统故障诊断研究的热点和难点[1]。

经验模态分解(Empirical Mode Decomposition,EMD)是一种自适应的非线性、非平稳信号分解方法[2]，在转子故障诊断中得到了广泛的应用[3-4]。但是，该方法存在模式混叠的现象。为解决这一问题,相关学者提出了集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[5]、噪声辅助多元经验模态分解(Noise Assisted Multivariate Empirical Mode Decomposition,N-A MEMD)[6]等噪声辅助方法,变分模态分解(Variational Mode Decomposition,VMD)[7]、经验小波变换(Empirical Wavelet Transform，EWT)[8]等基于滤波的方法。但噪声辅助方法存在噪声幅值、集合个数等参数选取困难，无法分离倍频程范围内的分量等不足。经验模态分解本质上是通过迭代对信号进行低通滤波以去除局部均值，从而分离出本征模态函数。现有基于滤波的方法构造截止频率恒定的低通滤波器进行滤波，不适合局部均值随时间改变的非平稳信号的分析。

基于此，Li等[9]提出了时变滤波经验模态分解(Time Varying Filtering EMD,TVFEMD)法。该方法克服了经验模态分解过程中的模式混叠现象，提高了信号在噪声和低采样频率下的鲁棒性，并且能够保持信号的时变特征，适合于非线性、非平稳信号的分析。林近山等[10]使用时变滤波经验模态分解的方法诊断齿轮箱的故障，取得了良好的效果。但是TVFEMD使用过程中，需人为设定带宽阈值和B样条阶数两个参数，具有较大的主观性，而且无法预知在所选参数组合下分解的有效性。因此，研究能够实现参数自动寻优的时变滤波经验模态分解方法，是十分必要的。Zhang 等[11]针对轴承、齿轮故障提出了改进的时变滤波经验模态分解方法实现参数自动寻优，但是衡量信号冲击性的加权峭度指标不适用于转子故障信号。寻找新的衡量指标并采用有效的寻优算法以实现转子故障信号TVFEMD过程的自动寻优十分必要。

本文以Hilbert边际谱部分频带能量比作为适应度函数，采用粒子群算法进行参数自动寻优，提出了参数优化时变滤波经验模态分解的方法，再将该方法和希尔伯特变换(Hilbert Transform,HT)相结合对转子故障信号进行时频分析，实现对转子故障的诊断。

1 时变滤波经验模态分解原理

时变滤波经验模态分解本质上是通过构造截止频率随时间变化的低通滤波器，来完成EMD分解过程中的迭代去除均值操作，并以局部窄带信号代替本征模态函数作为迭代停止条件。由于对于给定任意多分量信号x(t)，可以表示为一个双分量信号

x(t)=A(t)ejφ(t)=a1(t)ejφ1(t)+a2(t)ejφ2(t)

(1)

因此，只需考虑双分量信号的分解过程。对双分量信号进行时变滤波经验模态分解的基本步骤如下：

步骤1对x(t)进行希尔伯特变换，得到复解析信号的幅值A(t)和相位φ(t)，对瞬时相位求导可得瞬时频率φ′(t)。

(2)

步骤2确定幅值曲线A(t)的极小值和极大值所在的时刻{tmin},{tmax}以及幅值A({tmin}),A({tmax})。

步骤3对A(t)的极值点分别进行插值，所得曲线分别为β1(t)和β2(t)。

步骤4根据式(3)、式(4)计算出瞬时均值a1(t)和瞬时包络a2(t)。

a1(t)=[β1(t)+β2(t)]/2

(3)

a2(t)=[β2(t)-β1(t)]/2

(4)

步骤5令

(5)

(6)

(7)

(1)定义信号x(t)的极大值点的时间序列ui,i=1,2,3,...;

如果

(8)

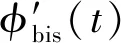
步骤7根据调整后的截止频率重构信号

(9)

将h(t)的极值点作为节点，将h(t)分成n段，每段步长为m。其中，n称之为B样条函数的阶数。使用式(10)～式(13)进行B样条插值逼近，逼近结果记为m(t)，代表局部均值曲线。

(10)

(11)

(12)

(13)

式中：[.]↓m为降采样，即每隔m个点进行采样；[.]↑m为过采样，即在每两个采样点之间插入m个采样点。

步骤8判断是否满足停止准则θ(t)<ξ，其中ξ为给定带宽阈值。如满足，x(t)为IMF；如不满足，令x(t)=x(t)-m(t)，重复步骤1～步骤7，直到满足停止准则为止，满足停止准则的x(t)为IMF。

(14)

(15)

(16)

2 参数优化时变滤波经验模态分解原理

TVFEMD执行过程中，需人为指定带宽阈值ξ和B样条阶数n两个参数，存在较大盲目性和不确定性。为实现参数的自动寻优，需首先定义目标函数，确定寻优算法。下面就本文所提Hilbert边际谱部分频带能量比作为目标函数的粒子群参数优化方法进行介绍。

2.1 Hilbert边际谱部分频带能量比

Hilbert 边际谱以概率的形式表示了每个频率上分布的整个时间序列累计的振幅或能量[12]。在边际谱中，不同的转子故障类型在转频及其分数谐波、倍频处表现出不同的特征，但故障特征频率集中于一定的时间和频率范围内[13]。参考文献[14]提出的轴承故障包络谱故障特征能量比指标来衡量解调效果，本文提出Hilbert边际谱部分频带能量比的指标来定量衡量转子故障信号TVFEMD的效果并作为粒子群算法寻优的适应度函数。该指标定义为边际谱0～5倍转频频带范围内能量与边际谱总能量的比值，其计算公式为

(17)

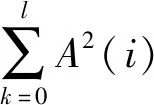
2.2 粒子群算法

粒子群算法是一种具备全局寻优能力的方法。X=(X1,X2,...,XM)代表M个粒子组成的种群，D维向量Xi=(xi1,xi2,...,xiD)表示第i个粒子的位置，向量Vi=(vi1,vi2,...,viD表示第i个粒子的速度，Qi=(qi1,qi2,...,qiD)为个体局部极值，G=(g1,g2,...,gD)为种群全局极值，各粒子通过式(18)和式(19)更新位置和速度

(18)

(19)

式中：ω为惯性权重;d=1,2,...,D;i=1,2,...,M;a为当前迭代次数;c1和c2为加速度因子;η为介于[0,1]的随机数。

2.3 参数优化时变滤波经验模态分解流程

步骤1初始化粒子群各参数。

步骤2以ξ和n的参数组合作为位置坐标，初始化粒子群的位置并随机初始化粒子群的速度。

步骤3在不同粒子位置下对信号进行TVFEMD，计算各个位置下的Hilbert边际谱部分频带能量比。

步骤4对比各个位置Hilbert边际谱部分频带能量比大小，初始化个体局部极值和整体局部极值。

步骤5利用式(18)和式(19)更新粒子群的位置和速度。

步骤6迭代循环，转至步骤3，直至迭代次数达到最大设定值后输出最佳适应度值和粒子位置。

3 诊断流程

基于参数优化时变滤波经验模态分解和希尔伯的转子故障诊断方法基本步骤如下：

步骤1确定参数寻优范围，初始化粒子群各参数。

Zhang等推荐带宽阈值0<ξ≤1。笔者经多次实验发现，随着ξ的取值接近于0，计算耗时增加，而且边际谱出现较多的特征频率外的成分干扰。一般ξ取值达到约0.1时即可获得较好的分解效果，边际谱图更加干净，计算速度较快。因此，本文中带宽阈值的寻优范围为0.1≤ξ≤1，B样条阶数的寻优范围在5≤n≤30，获得的参数组合在实际工程应用中已足够达到较好的分解性能。

参考文献[15-16]，并经过多次数值实验，本文中粒子群的参数设置见表1。

表1 粒子群算法参数设置Tab.1 Parameter setting of particle swarm optimization

步骤2使用粒子群寻优的最佳参数组合进行TVFEMD，获得若干IMF(Intrinsic Mode Function)。

步骤3对IMF进行HT，根据瞬时信息得到故障信号的Hilbert时频图和边际谱。

步骤4根据时频信息诊断转子故障类型。

4 实验验证

采用如图1所示的转子实验台验证本文所提方法的有效性和优越性。该实验台由圆盘转子、动压轴承、调速电机控制器、预紧力支架、ZonicBook/618E型信号采集设备、后处理计算机等设备组成。

4.1 恒定转速的转子不平衡故障

在转子圆盘转子45°的标记处安装1 g的不平衡质量来模拟转子不平衡故障。转子的转速为3 000 r/min，采样频率为2 560 Hz。分别在水平和垂直两个方向安装传感器采集信号，从水平方向的信号中任选连续的2 000点作为待分析信号。

图1 Bently RK4转子实验台和信号采集器Fig.1 Bently RK4 rotor test rig and signal collector

表2为在人为设定的不同参数组合下进行TVFEMD所得Hilbert边际谱部分频带的能量比值。

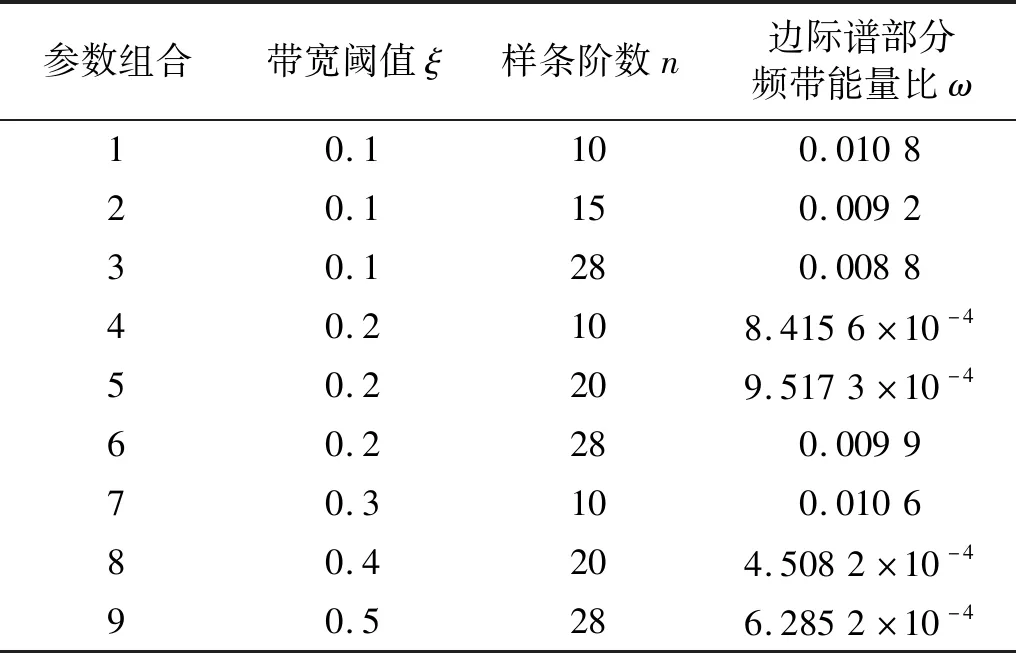
表2 不平衡故障不同参数组合的Hilbert边际谱部分频带能量比Tab.2 Partial spectrum energy ratio of Hilbert marginal spectrum with different parameter combinations for unbalanced faults

为对比分析不同参数取值时分解效果的差异，同时，验证使用边际谱部分频带能量比指标作为适应度函数衡量分解效果的有效性，现选取表2中能量比最大的参数组合1、居中的任意参数组合3以及最小的参数组合8，分别在三组参数组合下进行TVFEMD，得到Hilbert边际谱如图2所示。

图2(a)中可见清晰的基频及二倍频成分，且集聚性好，幅值较大；图2(b)虽然也存在清晰基频及二倍频成分，但与图2(a)相比幅值较低；图2(c)则完全无法分离出清晰的基频及倍频成分，分解的效果很差。可见随着边际谱部分频带能量比逐渐降低，其分解效果也随之变差。由此验证，使用Hilbert边际谱部分频带能量比作为衡量分离效果的指标是可行的。

同时，表2也表明不同的参数组合下进行TVFEDM所得Hilbert边际谱的部分频带能量比差距较大，且无明显规律性。因此，为达到良好的分解效果，适当的参数组合的选取十分必要。而人为选择参数存在较大的主观性和盲目性，使用优化算法获取最佳参数组合无疑具有重要的工程意义。

图3为使用粒子群算法进行参数寻优时Hilbert边际谱部分频带能量比随进化代数的变化曲线。粒子群进化到第5代即得到了信号最大的Hilbert边际谱部分频带能量比0.011 8。寻优所得最佳参数组合为ξ=0.31,n=13。在该参数组合下进行TVFEMD，结果如图4所示。

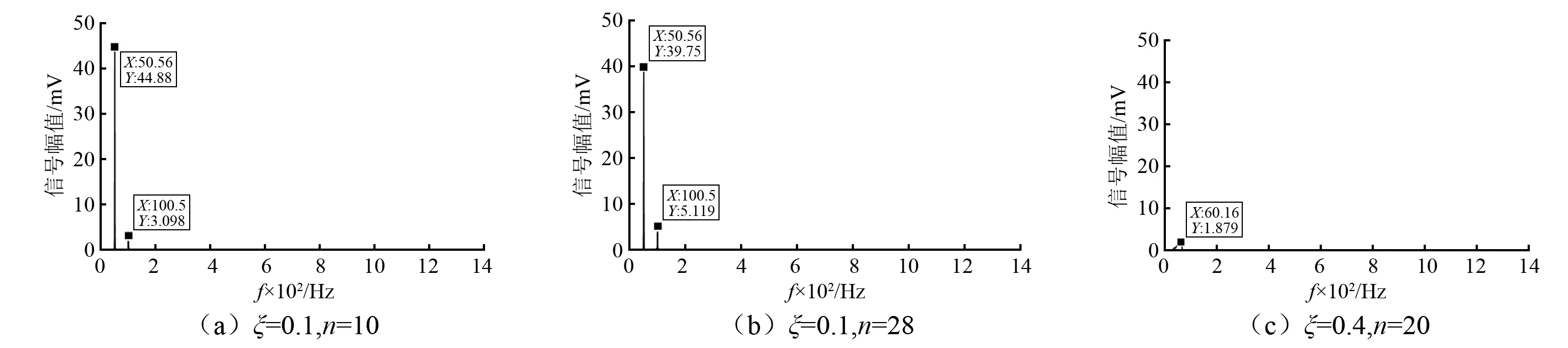
图2 不同参数组合下不平衡故障信号分解结果Fig.2 Decomposition results of unbalanced fault signals under different combinations of parameters

图3 不平衡故障Hilbert 边际谱部分频带能量比随进化代数的变化Fig.3 Hilbert partial spectrum energy ratio of unbalanced fault changes with evolutionary algebra

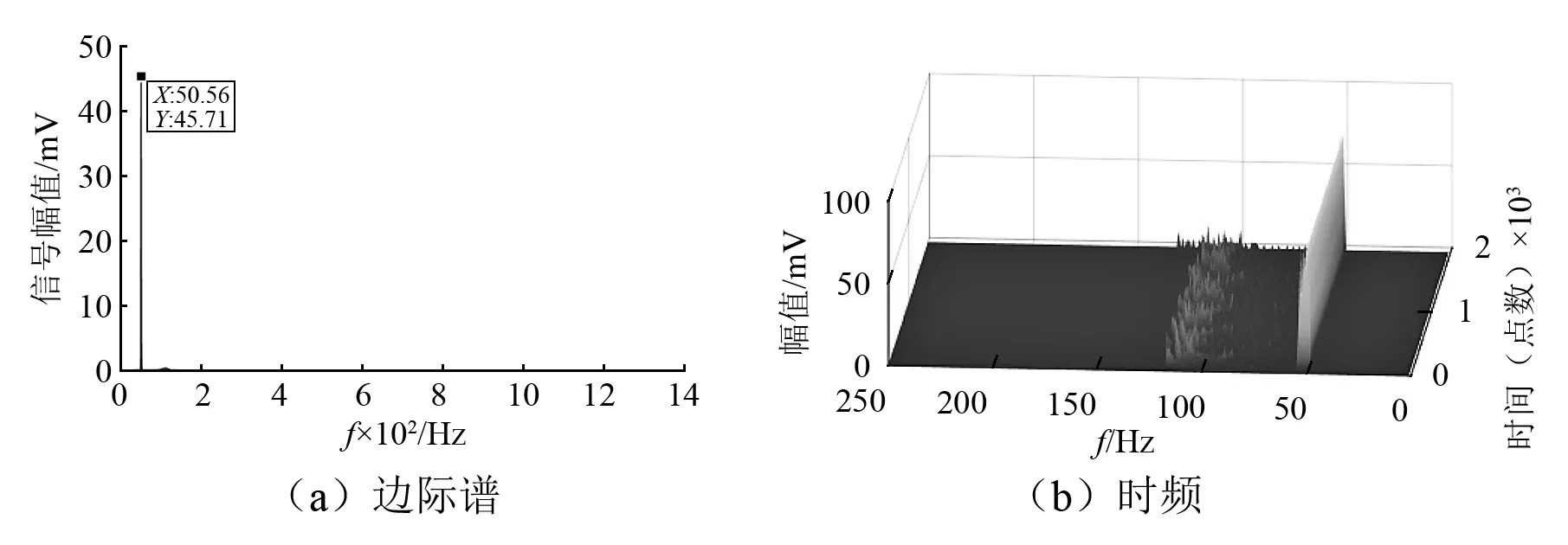
图4 不平衡故障信号使用本文方法分析所得Hilbert边际谱和时频图Fig.4 The Hilbert marginal spectrum and time-frequency diagram of the unbalanced fault signal are analyzed using this method

从图4可知，明显的50 Hz的转频成分，以及与基频相比微不足道的二倍频成分，不平衡故障特征明显。与图2(a)相比，基频的幅值更大，二倍频成分进一步压缩，分解的效果更好。图4中的时频图，基频集聚性强，不平衡特征明显。使用粒子群算法寻优的参数组合进行TVFEMD，能够有效的诊断不平衡故障，实现良好的分解效果。

为验证本文所提方法相比其他方法的优越性，分别使用原始EMD方法、文献[9]中的指定参数进行TVFEMD、文献[11]所提参数寻优方法对不平衡故障信号进行分析，结果如图5所示。其中，文献[9]采用ξ=0.1，n=28的参数组合；对实验采集的转子不平衡故障信号采用文献[11]所提基于相关峭度指标进行寻优所得参数组合为ξ=0.37，n=20。

图5 不同方法处理不平衡故障信号分析结果Fig.5 Analysis results of unbalanced fault signals processed by different methods

图5(a)所示采用原始EMD方法分析结果中，仅能发现幅值极小的基频附近成分。图5(b)所示采用文献[9]方法分析结果中，除基频外还存在幅值较为突出的二倍频成分。图5(c)所示采用文献[11]方法分析结果与图4所示采用本文方法进行分析的结果相比，集聚性较差，且边际谱基频幅值较低。总之，采用其他三种现有方法，无法突出故障特征频率，实现对故障类型的准确判断，而使用本文方法对故障信号进行处理故障特征频率突出，能够准确对不平衡故障进行诊断，从而验证了本文所提方法在转子恒定转速不平衡故障诊断中的优越性。

4.2 变转速的转子油膜涡动故障

为验证本文所提方法转子变转速工况下的适用性，采集实验台从1 400～2 000 r/min升速过程油膜涡动故障的振动信号，采样频率为1 280 Hz,采样点数为3 000。图6和图7分别为升速油膜涡动故障的时域波形和频谱。频谱中存在严重的频率模糊现象，无法准确提取故障特征频率。

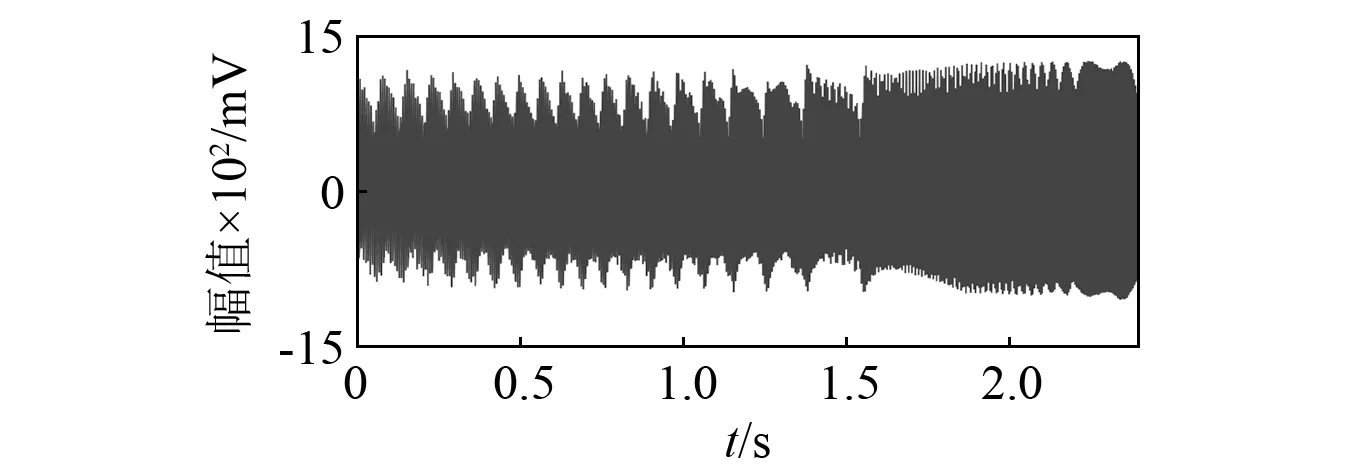
图6 升速油膜涡动故障的时域波形Fig.6 Time domain waveform of oil film whirling fault at rising speed

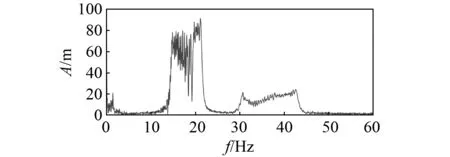
图7 升速油膜涡动故障的频谱Fig.7 Spectrum of oil film whirling fault at rising speed

图8为使用本文所提的方法对故障信号进行分析所得Hilbert边际谱部分频带能量比随进化代数的变化曲线。其中，对于变转速转子故障信号，粒子群进化到第3代即可得到最大的幅值能量比0.037 45。寻优所得最佳的参数组合ξ=0.12，n=20。在该参数组合下对故障信号进行分解，所得Hilbert时频图如图9(a)所示。图中能够清晰提取转频及其二分频成分，符合转子油膜涡动故障的特征，且集聚性较好，具有良好的分解效果。

图9(b)为采用原始EMD分析转子故障信号的Hilbert时频图，谱图中存在严重的频率模糊现象，无法准确提取故障特征频率。图9(c)为采用文献[9]指定的参数组合ξ=0.1，n=28进行TVFEMD和HT所得的Hilbert时频图。虽然也能较为清晰提取转频及其二分频，但特征频率处能量明显小于图9(a)采用本文方法分析所得结果。采用文献[11]所提出的相关峭度指标进行寻优，得到最优参数组合ξ=0.42，n=12，在该参数组合下进行TVFEMD和HT，所得Hilbert时频图如图9(d)所示。虽然能够准确提取转子的二分频，却无转频成分，与频谱所示的特征频率不一致，由此造成故障特征信息的丢失。总之，本文所提方法能够准确提取非平稳转子故障信号的特征频率，相比于其他三种方法具有明显的优越性。

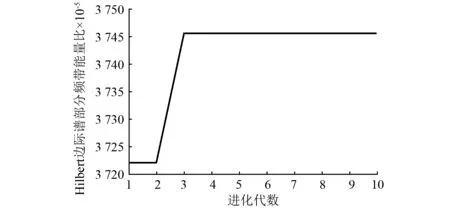
图8 油膜涡动故障Hilbert 边际谱部分频带能量比随进化代数的变化Fig.8 The variation of Hilbert marginal spectrum and partial band energy ratio of oil film whirling fault with evolution algebra

图9 升速油膜涡动故障信号不同方法分析Hilbert时频图Fig.9 Analysis of Hilbert time spectrum by different methods of rising oil film whirl fault signal

5 结 论

本文提出了一种基于参数优化时变滤波经验模态分解和希尔伯特变换诊断转子故障的方法。该方法以Hilbert边际谱部分频带能量比来定量衡量TVFEMD的分解效果，并作为粒子群寻优算法的适应度函数实现参数寻优；通过将分解所得的IMF进行HT得到的瞬时信息来诊断转子故障类型。分别将该方法应用于恒定转速下的转子不平衡和变转速下的油膜涡动两种典型转子故障，验证了该方法诊断转子故障的有效性和优越性，得到结论如下：

(1)使用Hilbert边际谱部分频带能量比作为衡量TVFEMD分离效果的指标是可行的。

(2)使用参数优化时变滤波经验模态分解结合希尔伯特变换对故障信号进行分析，能够突出故障特征频率成分，提高分解效果，从而有效的诊断非平稳转子故障。

(3)本文所提参数优化时变滤波经验模态分解方法相比于原始经验模态分解和现有方法相比能够克服模式混叠现象，更加准确提取故障特征频率，从而有效诊断转子不平衡、油膜涡动等典型故障。