基于Lamb波递归量化分析的复合材料裂纹损伤定征研究

刘小峰，杨康俊，柏 林

(重庆大学 机械传动国家重点实验室，重庆 400044)

复合材料层合板具有质量轻、成本低、比强度和比模量高等诸多优点，被广泛应用于航空航天产业和其它高新技术领域的同时，也给其基体微裂纹损伤和分层损伤的无损检测带来了挑战。在外力的作用下，基体微裂纹会引起层间应力集中，并随着微裂纹数量的增加，导致界面应力增加产生脱粘，显著降低了复合材料的压缩强度和刚度，而脱粘的扩展产生分层会导致最终结构的总体失效。Lamb波检测技术通过主动激发应力波对结构内部进行检测，可有效地感知粘接界面的变化，具有快速、长距离、大范围、成本相对低的特点，其在复合材料检测领域得到广泛应用[1]。但目前大部分基于Lamb波的复合材料板损伤检测主要集中在分层、孔或狭缝等后期严重损伤的检测与辨识方面[2]，而对复合材料早期出现的基体微裂纹的检测研究的文献还相对较少。Toyama等[3]研究了Lamb波速度如何受到基体微裂纹和分层的影响，却没有给出具体的检查方法。文献[4]采用了机器学习方法对基体微裂纹和分层的分类辨识进行了的初步研究，但未给出基体微裂纹的定量表征方法。文献[5]采用高斯判别方法对复合材料板中常规微损伤程度进行了分别识别，但尚未涉及基体微裂纹的损伤程度辨识。因此，对基体微裂纹的检测与定征研究对保证复合材料板的安全可靠的服役具有重要的研究意义。

复合材料的细观构造是一个复杂的各项异性多相体系，同时还具有较高的声衰减率，导致获取的Lamb波信号中噪声与损伤反射信号互相混杂，损伤信号波形不易分辨，信噪比低，这都给信号处理与损伤识别、定量评价带来了一定的困难。目前大多数Lamb波损伤特征提取方法都是基于平稳信号分析的时域或频域特征提取，而不同程度的基体微裂纹所引起的信号的特征在时域与频域上的差别不明显，再加上反射、散射波、模态转换波及噪声的影响与干扰，使得获取的Lamb波响应信号必然会表现出较强的非线性性、不确定性与复杂性。传统的Lamb波信号处理方法特征对微损伤程度缺乏足够的敏感性。目前的损伤波包识别方法[6-7]都缺乏损伤识别的可靠性、准确性、分析处理的快速性、恶劣检测环境的适应性。

针对以上问题，本文创新性地采用递归分析方法对复合材料的微损伤进行定征分析，并结合各项递归定量分析指数定义了复合材料损伤的统一表征指数UDI(Uniform Damage Index)，该指数对复合材料早期基体微裂纹损伤具有较好的敏感性，与损伤程度成良好的线性关系，为复合材料的损伤检测提供了一个有效可行的方法与手段。

1 递归图

递归图为揭示时间序列内部隐含的非线性系统内部信息提供了有效的定性分析方法。在状态空间内分析系统的动力学系统，确定系统的运动状态，就可以对系统进行完整的描述。在Lamb波对复合材料板进行无损检测时，可将Lamb波在板中的传播看作一个动力系统，这个系统是建立在Lamb波传播特性的基础上的，有许多可以描述其状态的变量，所有的这些变量可以支撑系统的相空间和状态空间。系统的状态会随着时间变化，其相应的Lamb波信号也展现出复杂的动力学行为。

当损伤尺寸较大，如基体微裂纹数目增多，严重分层时，这类损伤反射回波能量较大，其相应Lamb波信号的动力学非线性增强，导致其表现出来的递归特性有所不同。也就是，可将损伤状态下获得的Lamb波信号看作一个确定性的非线性动力系统，即可由该信号序列反推得到复合材料板损伤状态下的复杂的非线性动力系统。材料内部各个损伤间的多次散射、反射使得Lamb波的非线性特性增强，且内部损伤的发生具有明显随机性和不确定性。

递归图具有对演化规律的敏感性，因此每一种特征翻译了系统不同的演化规律，对于有限长度的信号而言则可以揭示信号内在的变化规律。如果复合材料板内部存在的基体微裂纹损伤增多，将导致反射与散射的Lamb波增加，而Lamb波反射及散射方向是多变的，考虑到超声换能器的位置和方向是固定的，因而可认为接受到的Lamb波信号的强度会随着裂纹的存在而改变，强度上可能变大也可能变相；另外基体微裂纹的分布具有较强的随机性，导致回波信号的随机成分增加，损伤对Lamb波的传播过程的影响具有显著的非线性特征，这从理论上支持了可以使用递归分析对Lamb波信号进行评价。

Lamb波信号的量化递归分析是利用损伤信号的混沌特性，分叉特征，子相似性及确定性，对复合材料板损伤状态下的结构动力学特性进行描述，从而达到对其内部损伤定征的目的。通常情况下，可以用相空间中的一个“点”来表示动态系统在该时刻的状态，对于d维动态系统在固定时刻t的状态可以用式(1)所示的向量来表达

(1)

这样的“点”称为相点。若该系统是一个连续时间系统，则其随时间的演化规律可以式(2)中的微分方程来表达，这样相点随时间的演化即在相空间中即构成了相轨迹。

(2)

有限的Lamb波时间序列，通过这些时间序列回复出结构系统相轨迹的几何结构并保持其基本性质，这就是相空间重构。根据Takens定理，对一个时间序列

X={yj|yj=[xj,xj+τ,…，xj+(m-1)τ]T}

(3)

式中：m为嵌入维数；τ为延迟时间；j=1,2,…,M,M=N-(m-1)τ为相空间中的相点个数。只要嵌入参数m和τ选取恰当，重构的相空间便于原系统相空间微分同胚。一般常选用互信息法[8]计算τ，用Cao[9]的方法计算m。递归图的定义是以相空间重构为基础的，它反映了重构后吸引子所具有的某种属性，不同性质的信号，其吸引子的表现不一样，递归图的结构也不同。递归图的数学表达式为

(4)

式中：Θ(·)为Heaviside阶跃函数；Θ(x<0)=0,Θ(x≥0)=1；‖·‖为距离范数；ε为递归阈值。当相空间中任意两点间的距离小于ε时，在递归图上显示为一白点，因此递归图表现为黑白图形来刻画时间序列[10]。递归图旨在显示化分析高维动力系统的相轨迹，其模式与系统特定的动力学行为相关。

2 递归定量分析(Recursive Quantitative Analysis,RQA)

尽管递归图能够展现系统状态随时间演化过程中的递归行为，但却无法对其进行定量描述。为了定量分析Lamb波信号中隐含的结构损伤信息，可采用递归量化指标[11]对递归图中的递归特性进行表征。基于递归图中递归点的密度，沿对角线纹理特征可定义如下5个参数指标，用以定量分析Lamb波激励下的复合材料板振动系统的递归行为。

确定率(Determinism,DET)：指两个以上的白点连成的对角线段在递归图中所有白点中占得百分比，用于描述系统的确定性变化。

(5)

式中:l等于组成线段的白点个数，代表对角线程度，lmin=2;p(l)为长度为l的对角线段出现的概率。

递归熵(Entropy,ENTR):对角线段的香农熵，通常表示系统变化的不确定程度。

(6)

捕获时间(Trapping Time,TT):递归点构成垂线或水平线段的长度，描述系统在某个特定状态下的平均保持时间。

(7)

平均对角线长度(L)：代表两段相轨迹在相空间中相互靠近的平均时间，即系统的平均可预测时间。

(8)

1型平均递归时间T1：反映了系统稳定性的程度，在重构相空间内，以参考向量点X0为中心，以临界距离ε为半径的球形区域内相应邻域点的集合定义为1型邻域点集合S1={Xt1,Xt2,…,Xti,…}，得到1型递归时间为{T1(i)=ti+1-ti,i=1,2,3,…}，取平均值即可得到1型平均递归时间T1。

(9)

式中：d1为系统的信息维数。

3 试验验证

3.1 疲劳循环实验

本文选择试验对象为美国航天局复合材料疲劳循环实验中的狗骨形复合材料层合板，其尺寸为15.24 cm×25.4 cm，铺层方向为[02/904]s，如图1所示。左端加工了一个凹槽，凹槽尺寸为5.08 mm×19.3 mm，经过加载和疲劳循环后，凹槽周围出现了微小基体微裂纹损伤。每次循环加载完成后，采用X光对板材进行扫描，记录其基体微裂纹的个数，具体信息如表1所示。

图1 复合材料试验板Fig.1 Composite test board

层合板上下布有12个传感器，编号为1～12，如图1所示，分别取传感器1～6作为信号激发器，传感器7～12作为信号接收器，共产生36组响应信号。激发信号是中心频率为250 kHz的5周期的汉宁窗调制波，信号的采样频率为12 MHz，每组信号采集2 000个点,取前1 024个点。从图1可知，路径5～7，5～8，6～8，6～9非常接近或者通过损伤区域，其对应的Lamb波信号最大程度上地包含了层合板损伤信息。

图2给出了工况1与工况6下，路径6～8上采集的Lamb波信号的时域波形图及其频谱图。从图2可知，不同损伤程度下的接受的Lamb波信号的不管在时域波形上还是其频谱成分上都极为相似。尽管可根据波包传播速度及其散射能量的变化，以直达波包传播时间及散射能量作为裂纹损伤程度的表征量，但这些时频域的特征量与损伤程度并不存在着较好的线性关系，无法对损伤程度进行准确的量化识别[12]。再者，在一般工程应用中，往往会产生直达波包与其他散射波包、反射波包混叠的情况，再加上噪声的影响，也会造成直达波包分离困难的问题。

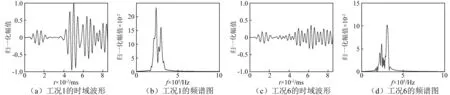
图2 不同工况下路径6～8上的Lamb波信号Fig.2 Lamb wave signal on path 6～8 for different conditions

3.2 递归图分析

分别对表1中不同工况下的路径5～8获得Lamb波信号进行递归分析。首先计算所用响应信号的嵌入维数m与时间延迟τ，进而可计算得到图3中的路径5～8不同工况下的Lamb波信号递归图。

从图3可知，每种递归图中的对角线分布并不相同，损伤程度大的情况的对角线的分裂较严重，并且白斑现象非常严重。这表明各路信号中反映的结构子相关特性与振动特性的各不相同。对角线代表了信号中固有的振动特性，各个子图中的带状结构，对角线的粗细也各不相同，这表示每个信号中的周期特性，自相关性也各不相同。随着微损伤个数的增加，递归图越来越分散(见图3)，在图3(a)～图3(d)4个递归图中，递归点相对比较集中，图3(e)～图3(f)中的两个递归图中，递归点就明显表现出分散性。可见，递归图未包含任何线性变化，是一种基于概率、普遍的提取结构振动特性的方法，可以作为用于提取损伤造成的Lamb波信号非线性特征的有效工具。

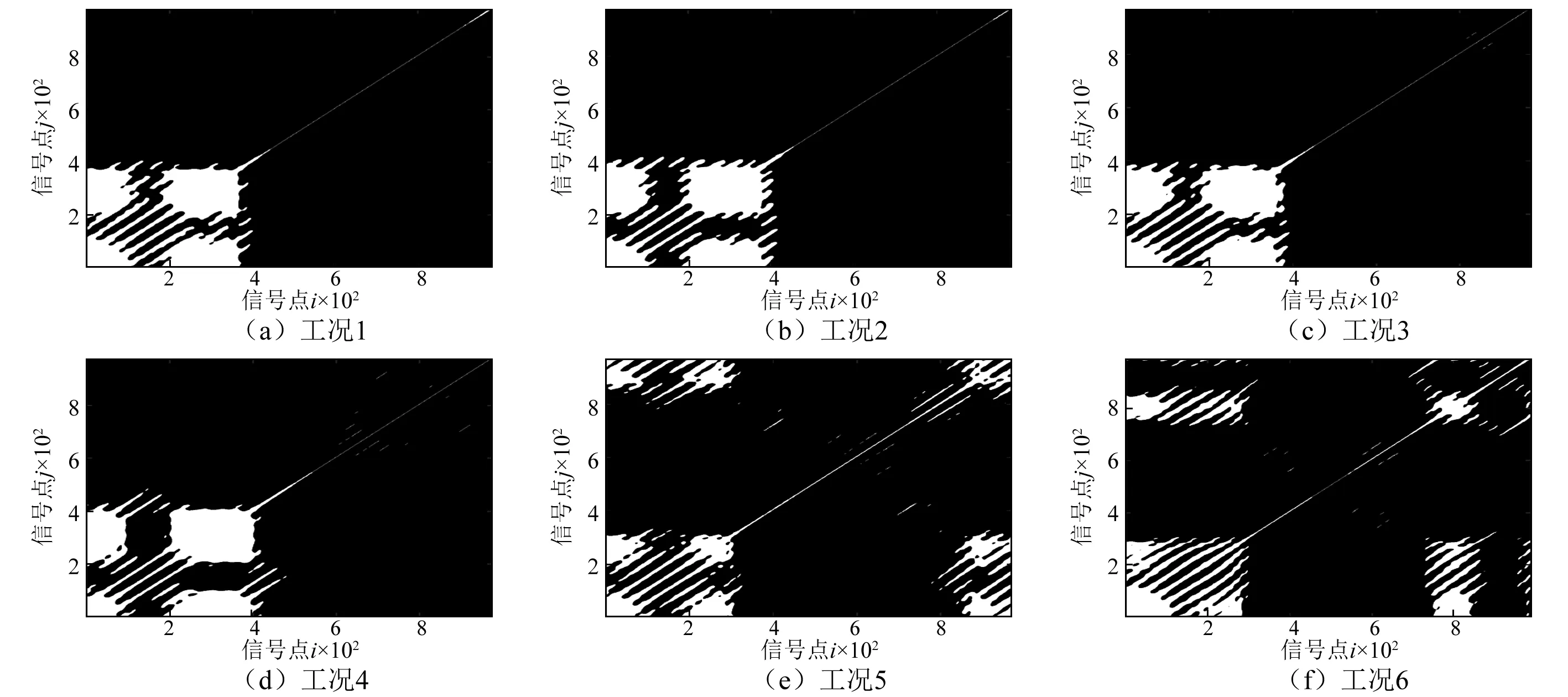
图3 路径5～8中6组信号的递归图Fig.3 Recursive plots of 6 groups of signals in path 5～8

3.3 递归量化分析

递归分析主要是利用总结归纳得到的递归图模式对一些简单的信号特征做出判别，而递归量化分析使用了量化分析手段，更适用于分析多散射多模态等复杂的Lamb波信号。递归量化指标是根据递归点在递归图上分布特征而计算得出的特征参数，根据式(5)～式(9)在递归图基础上得出的各种工况下各路信号的DET，ENTR，L，T1及TT值，如图4所示。

随着微损伤个数的增加，损伤信号增强，递归图上的递归点数减少，信号整体的递归性下降，因此出现了DET随损伤程度的增加而下降趋势(见图4(a))。随着微裂纹个数的增加，Lamb波信号的信息量增加，损伤信号更加明显，信号的不确定性减小，导致了ENTR的减小(见图4(b))。

随着微损伤个数的增加，接收的Lamb波信号的周期性越差，不同矢量之间的欧式距离会增大，相空间轨迹发散就越快，因此平均对角线L的长度越小(见图4(c))。获取的Lamb波信号的规律性降低，导致递归图的分散程度增加，从而造成递归图中垂直结构的平均长度减小，即TT的减小(见图4(d))。由于微损伤个数增多，相应的损伤信号也会会增强，增强信号经过相空间重构后，原本在1型邻域点集合内的重构向量会更靠近球边缘，而原本在球外的重构向量会进入到球中，导致系统的状态转换时间变大,即T1的增大(见图4(e))。由于试验板的损伤程度不仅与微损伤个数有关，而且还与损伤分布方向与位置有关系，因此，图4中RQA参数与损伤程度并不成完全的线性关系，但可用于表征试验板的损伤程度的变化趋势。

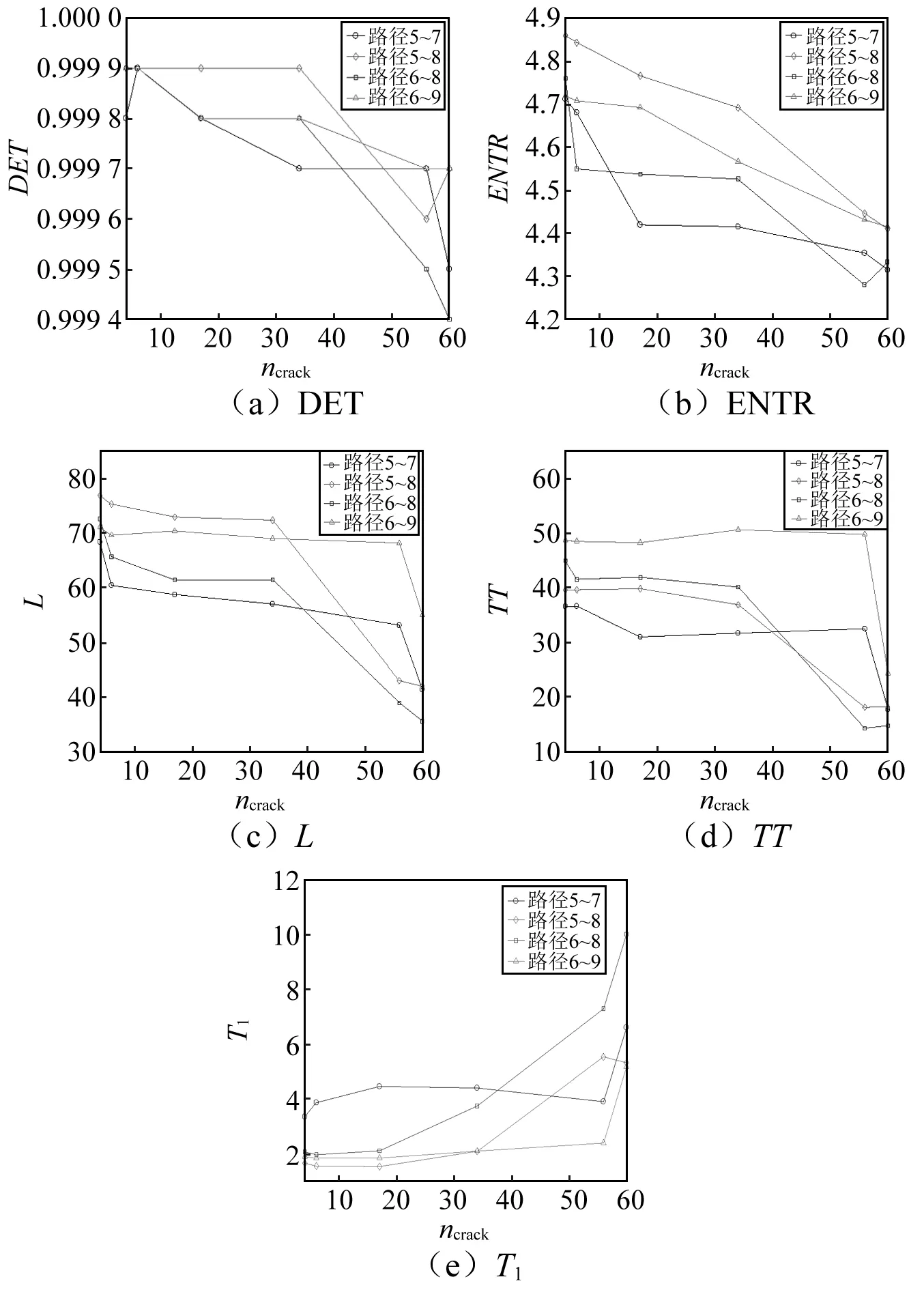
图4 RQA参数随损伤程度的变化趋势Fig.4 Trends of RQA parameters changes with the degree of defect

3.4 特征融合

从图4可知，不同的RQA特征参数对损伤程度的敏感度不同，鲁棒性也各不同。为了统一表示复合材料板的损伤损伤状态，有必要采用统一的融合指数对其损伤程度进行表征。由于表1中的工况1下的复合材料板近似可看作是无损状态，因此可将工1况下测得的RQA特征量作为基准，以损伤状态下的特征量与基准之间的偏差作为统一损伤指数，以表征试验板的损伤程度。将图4中的5个RQA表征参数进行归一化后，取其与工况1下的特征参数的欧式距离作为融合的特征值。设工况i与工况j下的RQA参数组成的特征向量分别为

Xi=[xi1,xi2,xi3,xi4,xi5],Xj=[xj1,xj2,xj3,xj4,xj5]

(10)

xi1,xi2,xi3,xi4,xi5分别为工况i下的Lamb波响应信号的DET，ENTR，L，TT，T1的RQA特征值。则Xi与Xj两者之间的欧式可表示为

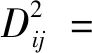
(11)

(12)

式中：α为无损与有损状态间的阈值，这里取0.052。

从图5可知，特征融合后的DI值与Larrosa等研究中的直达波包时域峰值，能量及功率谱密度峰值相比，其对基体微裂纹损伤的敏感程度明显较大，随着损伤个数的增加而成线性单调递增的趋势，更能对复合材料板的基体微裂纹损伤进行准确表征。但图5中各个路径上的DI-ncrack拟合直线的斜率各有不同，说明不同路径上的DI值对损伤程度的敏感度并不一样，越是靠近损伤区域的路径6～8上得到的DI敏感性越好。由于实际工程应用中损伤位置未知的情况下，路径的选择存在非确定性，因此，有必要将各个路径的DI值进行再次融合，得到试验板的最后的UDI。路径指数的融合方法如式(13)所示

(13)

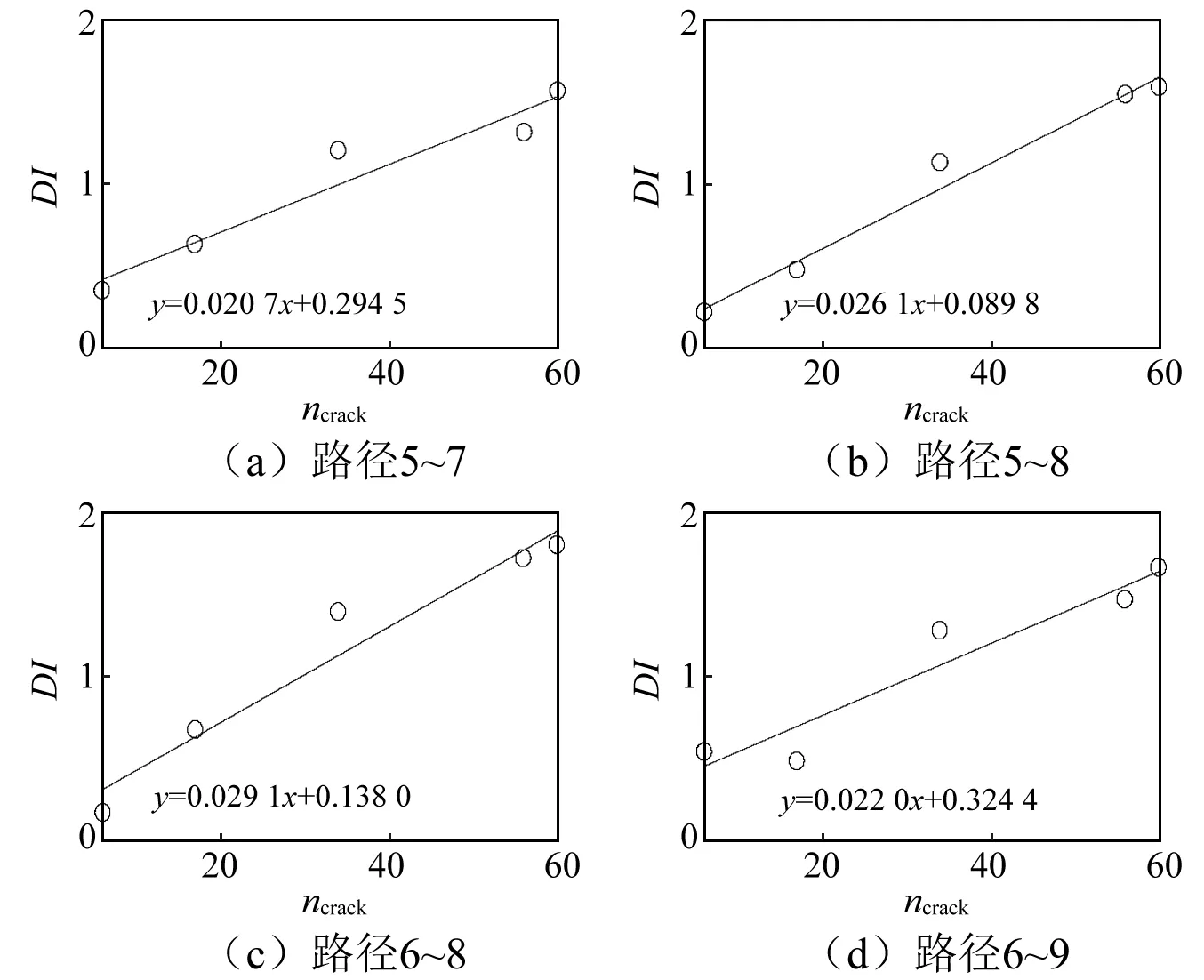
图5 DI值随微损伤个数的变化趋势图Fig.5 Trends of DI value changes with the number of micro-defects

式中：DIi=[DIi,5-7,DIi,5-8,DIi,6-8,DIi,6-9]，DIj=[DIj,5-7,DIj,5-8,DIj,6-8,DIj,6-9]分别为工况i与工况j下的各个路径上的DI值所构成的损伤指数向量；DIik与DIjk分别为工况i与工况j下的第k条路径中的得到的DI指数。在图5的DI值的基础上，采用式(13)得到的UDI值，如图6所示。

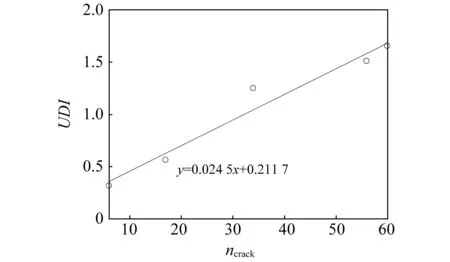
图6 FDI随微损伤个数的变化趋势图Fig.6 Trends of FDI changes with the number of micro defects

从图6可知，将多路径DI指数融合后，UDI随微损伤个数的增加表现出单调线性递增的趋势。UDI与损伤个数的变化之比为0.024 5，说明UDI值对复合材料中的基体微裂纹损伤程度具有较好的敏感性，能格准确表征试验板的损伤程度。

4 结 论

本文以Lamb波递归定量分析为基础，分析讨论了复合材料在不同疲劳循环次数下的基体微裂纹个数对应的损伤程度大小。为达到对复合材料板损伤进行统一描述，采用特征向量欧式距离将不同传感路径上的不同RQA指数进行了融合，提出了基体微裂纹损伤的UDI。分析结果表明，本文提出的UDI对复合材料基体微裂纹损伤具有较好的敏感性，与损伤程度成良好的线性关系，为复合材料的损伤检测提供了一个有效可行的方法与手段。本文旨在发展一种基于量化回归分析的Lamb波信号特征提取方法，建立信号特征与微裂纹损伤程度之间的映射关系，达到对复合材料板的基体微裂纹损伤进行定性定量检测的目的。