雨滴冲击荷载对斜拉桥拉索风雨激振影响的初步分析

李锦华，毛坤海，余维光，管海平，陈水生

(1.华东交通大学 土木建筑学院,南昌 330013；2.南昌铁路天河建设有限公司,南昌 330026)

风雨激振是指在特定风雨环境下，斜拉桥拉索发生的大幅振动，这非常容易造成斜拉索的疲劳破坏。Hikami等[1]对风雨激振现象进行了研究，并总结了许多关于风雨激振的基本特性；随后，大量研究如泉喷涌，主要为大量的现场实测[2]和风洞试验[3-4]探讨基本特性，然后通过力学分析建立理论方程进行分析。

风雨激振是由气体、液体和固体的三相耦合作用而产生，现象复杂，研究困难。目前主要的关注点有：Gu等[5]针对三维刚性节段模型进行风洞试验，拟合得到拉索气动力系数和水线气动力系数，并在水线运动方程中考虑了库伦阻尼力和黏滞阻尼力；张琪昌等[6]聚焦于风雨激振运动方程的求解方法，并运用混沌理论分析风雨激振的非线性特性，开拓了非线性方程的求解新思路；李暾等[7]讨论了连续拉索面内面外振动，在此基础上分析了多模态的耦合作用，并改进了库伦阻尼力的作用方式，认为其方向应该与水线的运动方向有关，使得水线运动方程更加完善；Wang等[8-9]的不同之处在于对水线运动方程的推导，他们运用滑移理论推导水线方程。总结之前的研究，主要在于水线运动方程的讨论及方程的求解，缺乏雨滴冲击对拉索振动影响的研究。考虑风雨激振的产生条件，雨滴冲击应该存在，但其影响则很难确定，因此其讨论显得非常必要。

雨滴冲击荷载作为外荷载而存在，若探讨它的作用，必须考虑风雨激振运动方程的形式。总的来说，风雨激振的运动方程有节段模型[10-11]和连续模型[12-13]两类。但本文的目的不是讨论运动方程，而是关注雨滴的冲击作用。为分析方便，采用节段模型进行分析。关于准运动水线单自由度节段模型，主要问题集中于对相对风速和相对风攻角进行处理。Wang等[14-15]忽略了相对风攻角式中分母项的水线项，并对相对风攻角在原点进行泰勒展开，对相对风速未做处理；Wilde等[16]的讨论选择忽略相对风攻角分母中水线项和相对风速中水线项，并在风攻角处进行泰勒展开；何向东等[17]则忽略相对风攻角和相对风速中所有的水线项。在这里所有的简化过程，最后的目的都是将相对风攻角和相对风速中包含的水线项及拉索振动项显式化，方便求解；然而这样处理却又导致了另外一个问题，使原本简洁的运动方程变得非常繁杂；为此相对风速和相对风攻角的处理方式就变得举足轻重。

由此，本文针对准运动水线单自由度节段拉索进行了雨荷载冲击的初步分析，并将分析过程分成三个部分进行讨论，分别为运动方程推导、处理方法比较及参数分析。由于雨滴冲击对拉索的作用，拉索运动方程将会有所不同，这部分将对这点进行详细讨论；尽管每位学者处理方法不同，但差别大小却不知道，故在第二部分将会对这个问题仔细分析；下面先讨论拉索运动方程。

1 考虑雨滴冲击荷载的拉索运动方程推导

传统在分析拉索风雨激振的时候，大多数学者往往将视角集中在水线形成后，拉索与水线耦合作用导致拉索的大幅振动，并分别对水线运动方程及拉索运动方程进行讨论；然而关于水线的形成条件及雨滴对拉索冲击力的影响则基本没有分析。基于此，本节的视角放在在整个风雨激振过程雨滴不断冲击作用，水线的形成条件需要大量实验取得统计结论，本文不做过多讨论。现实中，雨滴不断地撞击拉索，然后在拉索表面形成水线，并且这一过程与风速，雨滴质量及拉索表面材料等因素有关。于是就存在这样的两种可能：①雨滴均能黏附于拉索表面运动形成水线；②在特殊情况下雨滴均很难在拉索表面形成水线。为了考虑各种可能存在的情况，下面将分别基于这两种状态建立受雨滴冲击荷载作用的拉索运动方程。

1.1 无水线形成拉索运动方程

在降雨环境中，考虑拉索表面可能在特定强风速下难以形成水线。因此，在这一小节中，将讨论拉索表面不会形成水线，但有雨滴冲击时，拉索的运动微分方程。拉索实际振动情况非常复杂，在自然状态下很难精确地通过数学方程来表达。为此，进行基本假设：①不考虑拉索的面外振动，仅对面内振动分析；②节段拉索端部假定为铰接形式；③在计算微分方程时考虑拉索的静力构形作为计算初始条件；④由于拉索表面难以形成水线，因此认为雨滴与拉索之间的碰撞为完全弹性碰撞；⑤雨滴质量与拉索质量相比很小，可以忽略不计。

单位长度质量为mc，直径为的拉索Dc，其空间布置如图1所示。无水线拉索横截面模型如图2所示。斜拉索的大幅振动，主要是风和雨共同作用造成的。因此，在分析过程中，对风荷载及雨滴冲击荷载分别考虑。首先考虑风荷载的影响，当来流风速为U0，风向角为β，拉索倾角为α时，由于拉索只在动平面内振动，此时按照平行四边形法则将U0分解到与拉索动平面正交的平面内(后面称为正交平面)，在该平面内风速大小用U表示，风速与水平方向的夹角(风攻角)用γ表示，即

(1)

(2)

进一步考虑由于拉索本身振动对实际情况的影响。建立正交平面内风速与拉索振动速度矢量运算图(见图2)，可以得到相对风速Urel和相对风攻角φrel的表达式

(3)

(4)

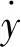
图1 拉索节段模型Fig.1 Segment model of a cable

图2 无水线拉索横截面模型Fig.2 Cross section model of no rivulets

Fa为竖向作用在拉索上的气动力，即在拉索上的气动升力和气动阻力在竖向的合力。说明：拉索在风雨共同激励时，尽管表面没有形成水线，但却处在降雨环境中，如果运动方程中的气动力系数采用无雨环境的风振气动力系数似乎不容易接受。因此，对于雨滴难以形成水线时考虑雨滴冲击荷载作用下的拉索风雨激励振动，运动方程采用降雨环境下的拉索气动力系数。

(5)

(6)

(7)

式中：CL和CD分别为升力系数和阻力系数，其中系数Ai和Bi的取值：A0=-0.390 9，A1=0.250 7，A2=1.762 5，A3=1.008 1，B0=1.555 5，B1=-0.538 2，B2=-0.885，B3=0.083 1；ρa为空气密度；φefc为有效风攻角，由于没有形成水线，故φefc=φrel。

接下来分析雨滴冲击荷载。根据风驱雨的研究可知，在水平方向上雨滴的运动速度最终会与风速无限接近，由此在雨滴降落时间足够长时，可以认为水平方向上风速即为雨滴运动速度。然后将风速分解到动平面内，如图1所示；由于拉索质量与雨滴相比非常大，考虑雨滴与拉索的碰撞为完全弹性碰撞，则应用冲量定理可得单个雨滴的冲击力，如下所示

(8)

Frs=4mr(U0sinαsinβ)2/Dr=2πρrDr2(U0sinαsinβ)2/3

(9)

式中：τ为作用时间；取Dr/(2U0sinαsinβ)；mr为雨滴质量；Dr为雨滴的有效直径；ρr为雨滴密度。

通过考虑M-P雨滴谱将单个雨滴的冲击力转化成大量雨滴的冲击力[18]，表达式如下所示

Fr=αDcFrsU0sinαsinβΔt/Ar=
2N0πρrDc(U0sinαsinβ)3Δt/(3λ4)

(10)

式中：α为雨滴在空气中的占有率；α=πDr3N(Dr)/6；N(Dr)为M-P雨滴谱，其形式为N(Dr)=N0exp(-λDr)，其中N0=8 000；λ为斜率因子，λ=4.1I-0.21，I为降雨强度。

拉索运动方程的建立。根据达朗贝尔原理，可知拉索运动方程如下所示

(11)

将式(5)和式(10)代入式(11)，得拉索运动微分方程如下

CD(φefc)sinφrel]/(2mc)-2N0πρrDc(U0sinαsinβ)3/(3λ4mc)

(12)

1.2 考虑水线拉索运动方程

在降雨环境中，考虑拉索表面形成水线。因此，在这一小节中，将讨论有水线形成，且有雨滴冲击时拉索的运动方程。首先进行如下假设：①不考虑拉索的面外振动；②上水线的振动频率与拉索相同；③上水线的初始位置是风速的函数，且水线运动形式为谐振动；④水线的质量很小，可以忽略不计；⑤认为下水线对拉索振动无影响，只考虑上水线的影响；⑥不考虑轴向流的作用；⑦在计算微分方程时考虑拉索的静力构形作为计算初始条件；⑧节段拉索端部假定为铰接形式；⑨由于水线的存在，认为雨滴与拉索之间的碰撞为完全非弹性碰撞；⑩忽略水线对拉索的压力；忽略水线与拉索之间的相互作用力。

拉索空间布置如图1所示，有水线拉索横截面模型如图3所示。首先考虑风荷载的影响，此时按照平行四边形法则将U0分解到正交平面内，在正交平面内风速大小用U表示，风速与水平方向的夹角(即风攻角)用γ表示，即

(13)

(14)

式中：ε为上水线对来流驻点影响的修正系数，本文修正系数取0.4。

图3 有水线拉索横截面模型Fig.3 Cross section model of rivulets

进一步考虑相对风速和相对风攻角，建立矢量运算图(见图3)，可以得到相对风速Urel和相对风攻角Urel的表达式分别为

(15)

(16)

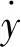
参考Wilde等假定水线的振动为谐振动，水线的振动幅值是风速的函数。本文假设水线运动满足该方程，即

(17)

式中：A为水线运动振幅；ω为水线振动频率(等于拉索固有频率)；Umax为当拉索产生最大振幅时的平均风速，采用试算法进行确定，系数a1和a2分别考虑为a1=0.448，a2=1.584 2。

上水线初始位置为平均风速的函数如下所示

(18)

则气动力如下所示

(19)

式中：φefc为有效风攻角，如下所示

φefc=φrel-θ-θi

(20)

下面分析雨滴冲击荷载。雨滴黏附于拉索表面运动，故考虑雨滴与拉索的碰撞为完全非弹性碰撞，根据图3，应用冲量定理可得单个雨滴的冲击力，如下所示

(21)

Fre=2mr(U0sinαsinβ)2/Dr=πρrDr2(U0sinαsinβ)2/3

(22)

式中：mr为雨滴质量；Dr为雨滴的有效直径；ρr为雨滴密度。

通过考虑M-P雨滴谱将单个雨滴的冲击力转化成大量雨滴的冲击力，表达式如下所示

Fr=αDcFrs/Ar=N0πρrDc(U0sinαsinβ)2/(3λ4)

(23)

式中：α为雨滴在空气中的占有率，α=πDr3N(Dr)/6，N(Dr)为M-P雨滴谱，其形式为N(Dr)=N0exp(-λDr)，其中N0=8 000，λ为斜率因子，λ=4.1I-0.21，I为降雨强度。

根据D′Alembert原理推导出拉索单自由度振动微分方程为

(24)

将式(19)和式 (23)代入式(25)，整理后可得拉索运动微分方程

(25)

通过比较式(10)和式(23)，发现在雨滴冲击荷载公式中并不包含拉索振动项，故可以明确这样一个问题，雨滴冲击荷载是可以独立出来的，与拉索的振动无关，因此在分析雨荷载的冲击时可以单独考虑；此外可以知道，两种情况下的雨滴冲击荷载是两倍关系，然而实际情况是介于这两者之间，于是针对冲击荷载引入冲击系数μ，如下所示

Fr=(1+μ)N0πρrDc(U0sinαsinβ)3/(3λ4)

(26)

式中：μ的取值范围为0～1，且当取值为1时应运用式 (12)进行计算。

则有冲击荷载的拉索风雨激振运动方程如下所示

(27)

2 风雨激振运动方程不同简化方式比较分析

通过前面的讨论，建立了有雨滴冲击荷载的拉索振动微分方程；而且可以知道雨滴冲击荷载是独立的，与拉索本身的振动无关，因此在分析方程其他问题时可以将雨滴冲击荷载暂时忽略。在准运动水线风雨激振方程中，水线与拉索的耦合导致运动方程非常复杂。为方便求解，许多学者针对该运动方程提出了不同的简化方法，而这些简化对最后结果的影响目前并没有被详细讨论。然而随着计算工具的不断发展，现在可以直接求解拉索风雨激振方程，不需要简化。故本节讨论的问题是，未施加冲击荷载时，简化方程与未简化方程求解拉索运动方程的差别。

以单位长度质量为10.2 kg，阻尼比为0.007，直径为0.14 m的节段拉索为例进行讨论。对拉索施加平均风速，得到在不同风速情况下拉索振动时程曲线。取固有频率为1 Hz的拉索，绘制时程曲线如图4～图7所示，其中图4为Wilde等模型1的简化形式，图5为Xu等的简化形式，图6为何向东等的简化形式，图7为未进行简化时拉索振动时程曲线，风速分别为9 m/s，11.6 m/s，15 m/s时拉索振动曲线。首先比较时程曲线，可以看到图4和图7比较接近，图5和图6差距较大，这说明Wilde等的简化方式所计算的结果更加接近未简化方程的数值解。其次绘制风速-振幅曲线，如图8所示，频率分别为1 Hz，2 Hz，3 Hz时拉索振动曲线。从总体上来看基本都符合风雨激振的基本特性，皆随风速先增大后减小，而Wilde等的简化方式中数值更加接近未简化的值。

图4 Wilde等模型1的拉索振动曲线Fig.4 The cable oscillation curve of wind induced vibration of Wilde,et al model 1

图6 何等的拉索振动曲线Fig.6 The cable oscillation curve of rain-wind-induced vibration of He,et al

图7 未简化的拉索振动曲线Fig.7 The cable oscillation curve of rain-wind-induced vibration of no simplification

3 风雨激振不同情况分析

通过比较简化与未简化之间的差别，可以知道简化方法非常重要，未处理好对结果影响非常大，甚至改变振动特点；此外，在简化过程会形成复杂的公式，容易疏忽，将公式弄错，这也会造成不小的问题。基于这个考虑，在可以求解的情况下，本文认为运用原始方程讨论更加合理。从两个方面进行讨论：①形成水线的条件下，施加冲击荷载与不施加冲击荷载时拉索振动的差别，同时对冲击系数μ及降雨强度进行讨论；②未形成水线的条件下，施加冲击荷载与不施加冲击荷载时拉索振动的差别，及不同降雨强度的影响。

讨论①：首先讨论能形成水线的情形；拉索属性同前，取冲击系数值为0.5，可以得到固有频率为1 Hz，2 Hz和3 Hz的拉索在不同风速时的振幅，分别绘制成拉索的风速-振幅曲线如图9所示。从图9可知，当风速为5～17 m/s时，施加冲击荷载的振幅曲线几乎与未施加冲击荷载的振幅曲线重合，这说明在这个风速范围内雨滴冲击荷载的影响很小几乎可以不考虑。

图8 不同频率拉索的风速-振幅曲线Fig.8 The curve of wind speed-amplitude of the cable with different frequency

图9 不同频率拉索的风速-振幅曲线Fig.9 The curve of wind speed-amplitude of the cable with different frequency

图10 冲击系数-振幅曲线Fig.10 Impact coefficient-amplitude curve

讨论②：针对无水线的讨论如下；拉索属性同前，取冲击系数值为0.5，可以得到拉索在不同风速时的振幅，绘制成风速-振幅曲线如图12所示。从图12可知，当风速为30～80 m/s时，施加冲击荷载的振幅曲线远大于未施加冲击荷载的振幅曲线，且随着风速的增大它们之间的差距越来越大，这说明在这个风速范围内雨滴冲击荷载的影响非常大，不能忽略。同讨论①，降雨强度振幅曲线如图13所示，从图13可知，随着降雨强度的增大，拉索振幅会减小，但是差距并不是很大；说明降雨强度会影响冲击力大小。

图11 降雨强度-振幅曲线Fig.11 Rainfall intensity-amplitude curve

图12 无水线的风速-振幅曲线Fig.12 Wind speed-amplitude curve of no rivulet

图13 降雨强度-振幅曲线Fig.13 Rainfall intensity-amplitude curve

在本小节从两个方面讨论了冲击荷载的作用，首先是低风速能形成水线的情况，通过分析发现，在低风速范围内雨滴冲击荷载的影响很小几乎可以不考虑；然后分析了在强风环境下的雨滴冲击作用，知道雨滴冲击荷载的影响非常大，且随着风速的增大它们之间的差距越来越大。由此得出结论，在低风速环境下雨滴冲击荷载可以忽略，在强风环境时，雨滴冲击荷载较大，不能忽略。

4 结 论

(1)传统对拉索施加雨滴冲击荷载的讨论还比较少，从风雨环境来说，风雨荷载肯定会同时存在，对风雨环境下拉索承受雨滴冲击荷载进行了讨论。由于拉索与雨滴之间的相互作用，在考虑雨滴冲击时，必须考虑拉索本身的振动对雨滴冲击力的影响，通过动量定理对其的分析，可以发现由于雨滴质量与拉索质量相比非常小，关于雨滴冲击力的计算，可以忽略拉索本身振动的影响，即雨滴冲击力可以作为单独的部分进行讨论。

(2)关于风雨激振准运动水线方程的求解问题一直以来都非常重要，许多学者对单自由度准运动水线进行了处理，本文比较了几种不同的处理办法对最后结果的影响，Wilde等简化处理比较接近未简化的结果；但是在简化的过程中很明显会使方程变得更加复杂，在可以求解方程的情况下，显然采用原方程将会更加简洁明了。

(3)关于冲击力对拉索的影响有多大，对于这个问题分别从低风速能形成水线和高风速不能形成水线两个方面进行了讨论，结果表明在低风速环境下雨滴冲击荷载的影响很小可以忽略，而在强风环境时冲击荷载则非常大，随风速的增大而增大。