含初应力周期性局域共振Mindlin板的衰减域特性研究

刘心男，刘 妍，纪颖波

(北方工业大学 土木工程学院，北京 100144)

周期性结构具有独特的衰减域特性，频率位于衰减域范围内的弹性波/声波无法在周期性结构中传播，从而使得周期性结构在振动控制、工程隔震和隔声降噪等领域具有重要的潜在应用价值[1-2]。

由于周期性结构的组成材料之间材料参数差异较大，在其生产和使用期间，初应力广泛存在[3-4]。早在1982年Anderson[5]在研究航空领域周期性网架结构动力特性时，便注意到外部静力荷载产生的初应力对周期性网架特征频率的影响，但当时周期性结构的衰减域特性尚未被发现，初应力对周期性结构动力特性的影响问题并未引起学者的重视。之后，随着周期性结构研究和工程应用的发展，外部荷载作用下周期性结构衰减域特性问题受到越来越多的关注。Qian等[6]采用传递矩阵法研究了初应力下周期性压电陶瓷/聚乙烯层状结构中剪切波传播问题，发现随着外部压力增加，剪切波波速逐渐减小。魏唯一等[7]对周期性压电/压磁层状结构中剪切波衰减域特性进行了研究，理论计算结果表明存在一个外部荷载临界值，当初应力小于临界值时可忽略初应力对衰减域特性的影响。Feng等[8-9]对外部压力作用下周期性钢/树脂杆件进行了试验研究，指出外部压力通过改变树脂基体的泊松比进而改变了周期性钢/树脂杆件的衰减域特性。Liu等[10]将弱形式求积元法引入周期性结构衰减分析中，研究了初应力作用下周期性二组元地基板的衰减域特性。

根据产生机理的不同，衰减域可分为由材料和几何周期性主导的布拉格散射型衰减域和由振子振动局域化主导的局域共振型衰减域[11]。现有的含初应力周期性结构研究中以布拉格散射型周期性结构为主，其衰减域的中心频率对应波长与周期性单元尺寸相当，故衰减域频率较高，主要应用于隔离高频振动。局域共振型衰减域可实现“小尺寸控制大波长”，有望应用于隔离低频振动。然而，初应力作用下周期性局域共振衰减域特性一直未能得到系统研究。本文将弱形式求积元法拓展至含初应力周期性局域共振Mindlin板衰减域特性研究中，系统分析初应力和几何参数对衰减域的影响，并分析有限周期局域共振Mindlin板的动力响应。本研究可为含初应力的周期性局域共振板应用于低频隔振提供理论基础。

1 控制方程及计算方法

周期性局域共振板由散射体、包裹层和基体组成，如图1所示。根据周期性结构理论，计算无限周期性结构衰减域时，可取任意周期性单元进行动力特性分析。

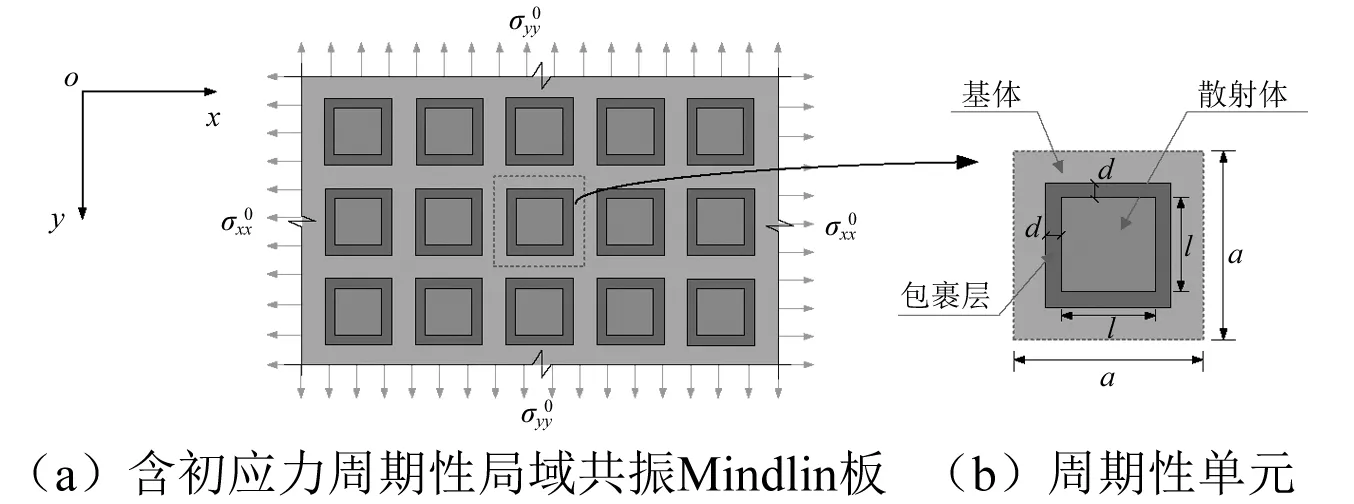
图1 含初应力周期性局域共振Mindlin板及周期性单元示意图Fig.1 Configuration of initially stressed periodic local resonant Mindlin plate and a typical unit cell

为应用弱形式求积元法，需先将周期性单元进行域分解。设板的横向位移为w，沿y和x轴的转角分别为ψx和ψy。任意子域e的应变能为

(1)

任意子域e的动能为

(2)

式中：ρ为材料密度。

任意子域e的外力势能为

(3)

式中：f为剪力;Mx和My分别为沿y和x轴的弯矩。

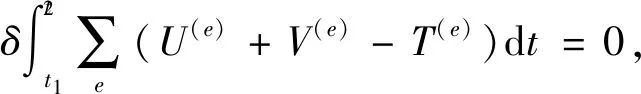
(4)

式中：M为质量矩阵；K为刚度矩阵；K0为几何刚度矩阵；d为节点位移矢量；F为节点荷载矢量。

设简谐波的圆频率为ω，波矢为k=(kx+iεx)ex+(ky+iεy)ey，其中，实部kx和ky分别为x和y方向上的相位因子，虚部εx和εy分别为x和y方向上的衰减系数。根据Bloch定理[13]，周期性边界条件满足

dr=e-εxaeikxadl,dt=e-εyaeikyadb

Fr=-e-εxaeikxaFl,Ft=-e-εyaeikyaFb

(5)

式中：位移和荷载矢量的下标l，b，r和t分别为周期性单元左边界、底边界、右边界和顶边界上的节点。

将式(5)代入式(4)得

(6)

对任意给定的波矢k，通过求解式(6)中矩阵特征值，可得相应的频率ω。根据周期性结构理论，当波矢取值遍历第一不可约布里渊区，即可获得该周期性局域共振Mindlin板中弯曲波的频散曲线。对任意给定的频率ω，并将相位因子取值限定在第一不可约布里渊区内，通过式(6)可求得衰减系数。

2 计算方法有效性验证

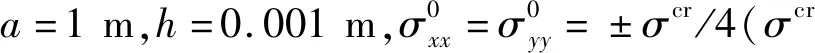
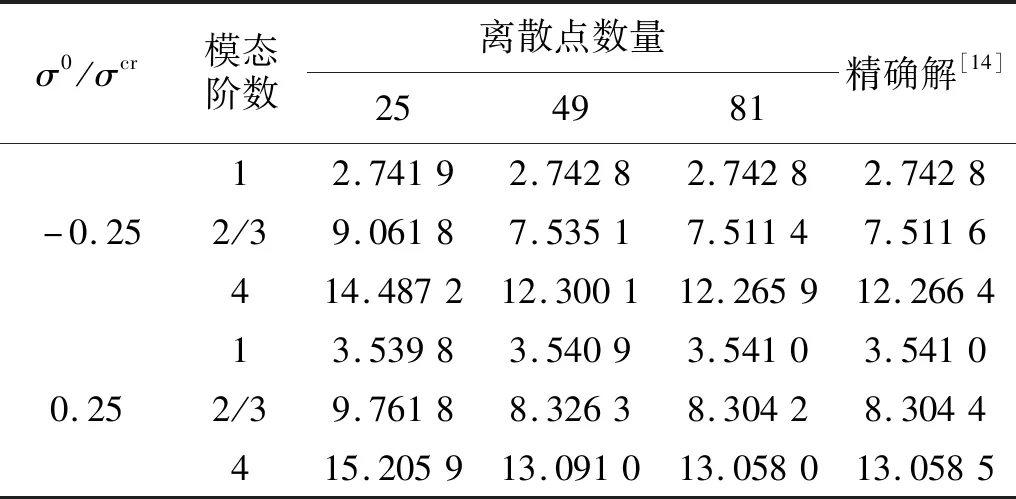
表1 初应力作用下四端简支均质板的前四阶特征频率Tab.1 The first four natural frequencies of SSSS homogeneous plate subjected to isotropic initial stress

3 参数分析

周期性局域共振Mindlin板中散射体为钢，包裹层为橡胶，基体为混凝土，材料参数见表2。取a=0.5 m，l=0.2 m，d=0.1 m，h=0.1 m，无初应力时周期性局域共振Mindlin板中弯曲波的频散曲线见图2。衰减域范围为4.8～7.4 Hz，对于该衰减域范围内的任意频率，在频散曲线上找不到与之相对应的波矢，这便是衰减域内的波无法在无限周期性结构中传播的原因。实际工程中周期性结构均由有限周期性单元组成，衰减域范围内的波将被有效地衰减。此外，衰减域范围内存在一条平直的频散曲线，后文将分析该平直带的产生机理。

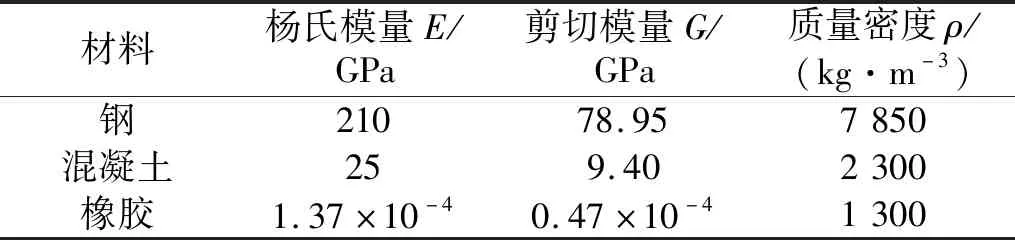
表2 材料参数Tab.2 Material properties

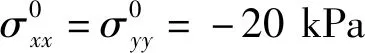
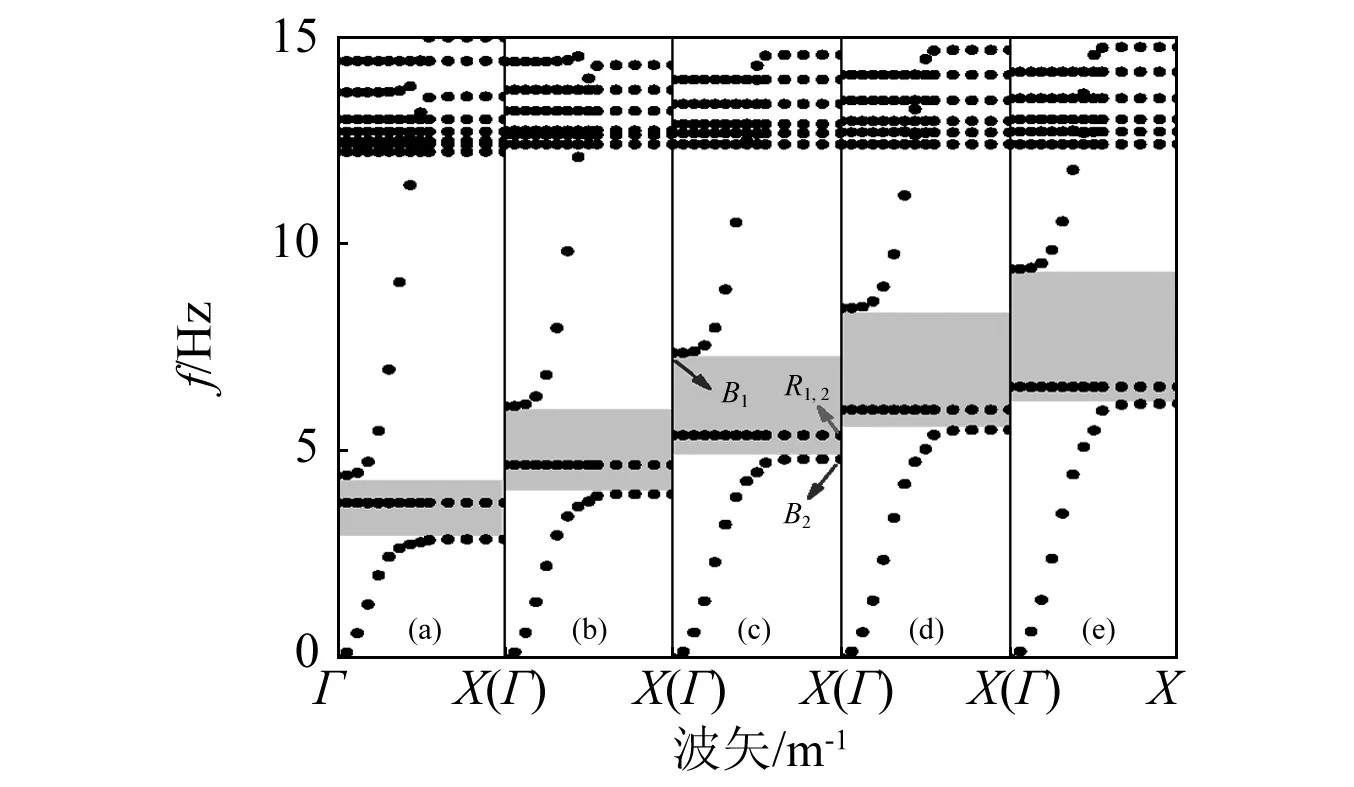
无初应力；图3 不同初应力作用下的衰减域Fig.3 Attenuation zones for various initial stresses

频率B1处，振动集中在散射体，基体没有发生位移，此时包裹的作用类似连接振子的弹簧。频率B2处，基体振幅最大，且与散射体振动反相。频率R1和R2处，基体保持静止，散射体绕其对称轴作刚体转动，该频率仅取决于散射体和包裹层的刚度及几何尺寸，而与波矢方向无关，故在频散曲线中表现为平直带。对于频率B1，R1，R2和B2，相较于基体和散射体，初应力对包裹层刚度的影响更为显著。随压/拉初应力增大，包裹层和周期性单元刚度降低/增加，从而导致了图3中衰减域随初应力的变化趋势。

图4 频率B1，B2，R1和R2处的模态Fig.4 Mode shapes at the frequencies B1,B2,R1 and R2

不同初应力作用下的衰减系数见图5。由于Fano干涉现象[15]，局域共振型衰减域的起始频率处衰减系数最大，然后迅速减小，直至衰减域终止频率处减小到0。此外，衰减系数随压初应力增大而减小，随拉初应力增大而增大。这意味着压初应力减弱了衰减域内波的衰减程度，与之相反，拉初应力增强了衰减域内波的衰减程度。

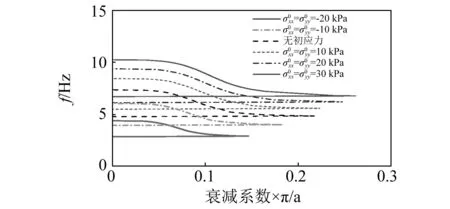
图5 不同初应力作用下的衰减系数Fig.5 Attenuation coefficients for various initial stresses

讨论几何参数对衰减域的影响时，当某几何参数改变时，保持其余几何参数不变。不同周期性单元边长下的衰减域，如图6所示。随周期性单元边长的增大，衰减域宽度迅速减小。当周期性单元边长足够大，该低频衰减域将会消失。此外，衰减域起始频率不随周期性单元边长的改变而改变，这是因为该起始频率仅取决于散射体和包裹层组成的“振子系统”的共振频率(见图4(a))，而不依赖于基体尺寸。不同包裹层厚度下的衰减域，如图7所示。随包裹层厚度的增加，衰减域向低频移动。这是因为包裹层越厚，散射体和包裹层组成的“振子系统”和整体周期性单元的刚度越小，衰减域的起始和终止频率越低。不同散射体边长下的衰减域，如图8所示。由于保持包裹层厚度不变，随散射体边长的增大，散射体和包裹层组成的“振子系统”的共振频率降低，衰减域起始频率降低。

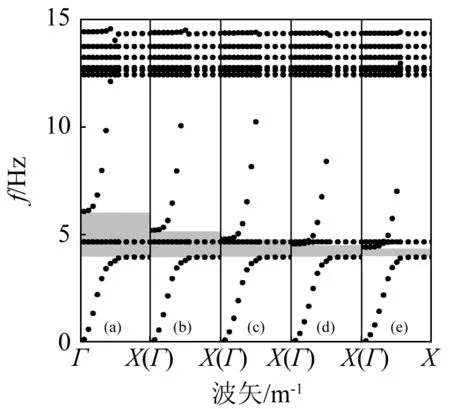
(a)a=0.5 m;(b)a=0.6 m;(c)a=0.7 m;(d)a=0.8 m;(e)a=0.9 m图6 不同周期性单元边长下的衰减域Fig.6 Attenuation zones for various periodic constants a

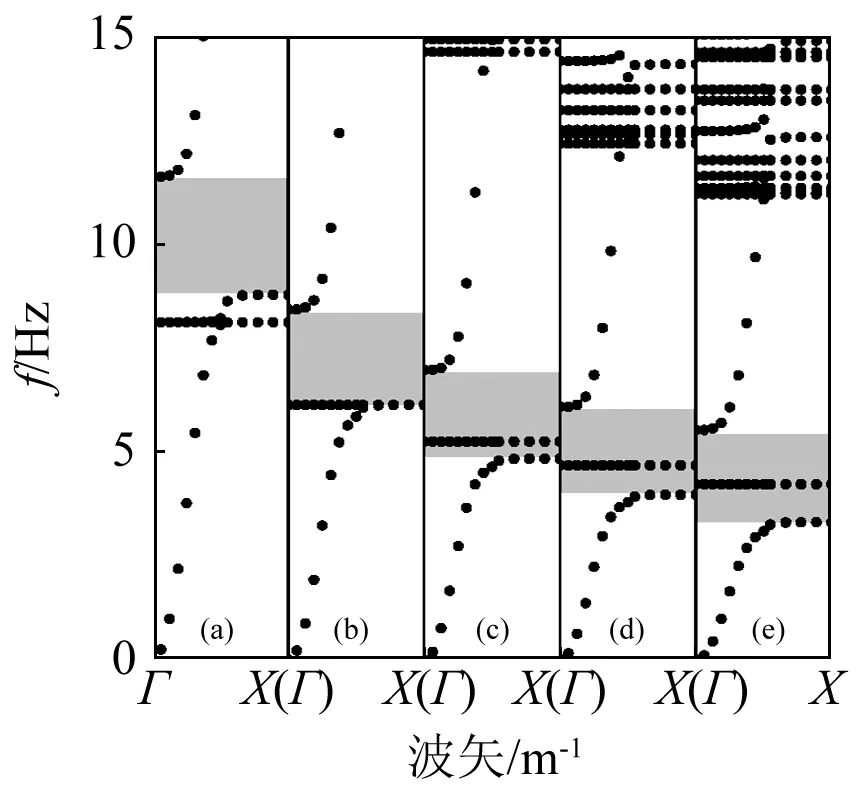
(a)d=0.025 m;(b)d=0.05 m;(c)d=0.075 m;(d)d=0.1 m;(e)d=0.125 m图7 不同包裹层厚度下的衰减域Fig.7 Attenuation zones for various thicknesses of the coating layer d

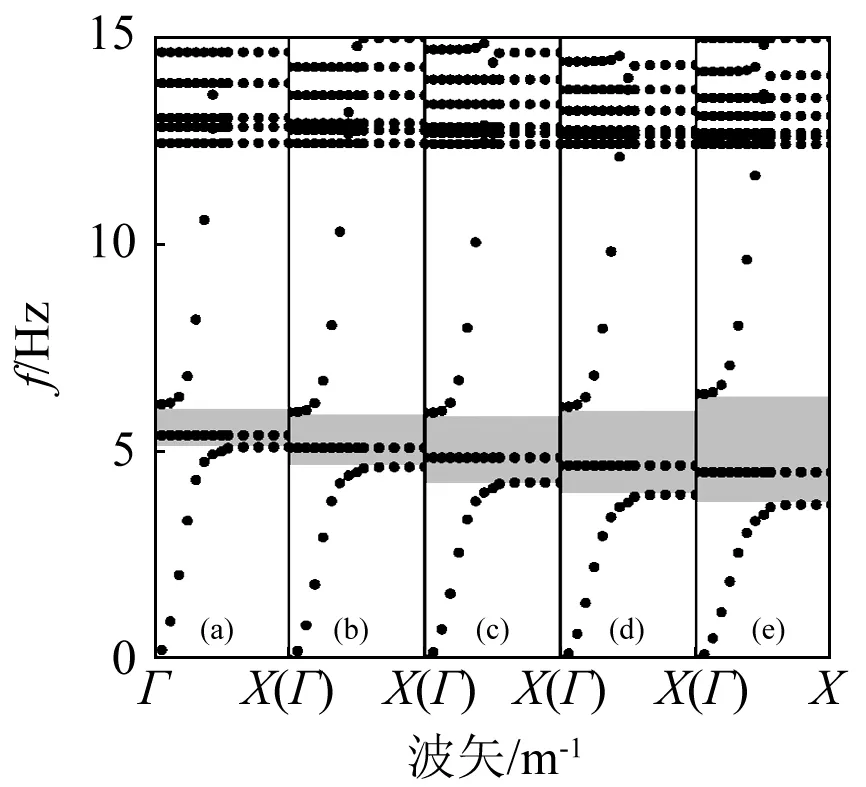
(a)l=0.125 m;(b)l=0.15 m;(c)l=0.175 m;(d)l=0.2 m;(e)l=0.225 m图8 不同散射体边长下的衰减域Fig.8 Attenuation zones for various side lengths of the inclusion l

4 动力响应分析

上述衰减域计算结果是假设周期性板在x和y方向上由无限周期性单元组成，而工程实际中周期性板为有限周期。本节考虑由x方向上5个周期性单元和y方向上无限周期性单元组成的有限周期性Mindlin板。y方向上取一个周期性单元，并施加周期性边界条件，dt=db和Ft=-Fb。对x方向上的一端施加单位位移激励，对另一端施加自由边界条件，计算其位移响应。

为量化有限周期性板中振动衰减程度，定义位移响应函数为20lg(w0/wi)，其中，wi和wo分别为x方向上输入端的位移激励幅值和输出端的位移响应幅值。负值的位移响应函数代表激励被有限周期性板有效衰减。取a=0.5 m，l=0.2 m，d=0.1 m，h=0.1 m，有限周期性板位移响应函数，如图9所示。由图9可知，无限周期性板的衰减域与有限周期性板中激励有效衰减频率范围吻合良好。此外，压初应力使有效衰减频率范围向低频移动，拉初应力使有效衰减频率范围向高频移动，验证了初应力对衰减域影响的分析结果。为进一步验证初应力对衰减系数影响的分析结果，取激励频率偏离衰减域起始频率0.1倍衰减域宽度，即f=fB1+0.1×(fB2-fB1)。有限周期性板中位移分布，如图10所示。对于衰减域内的激励，振动主要集中在前两个周期性单元，并随着振动在有限周期性板中沿x方向传播，其幅值逐渐减小。此外，含拉初应力、无初应力、含压初应力三种情况下激励的衰减程度逐渐减小，与图5中计算结果一致，验证了初应力对衰减系数影响的分析结果。

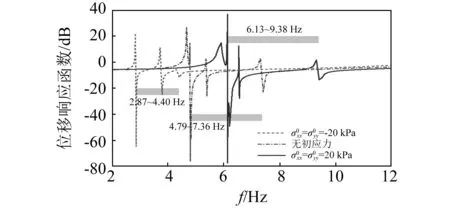
图9 位移响应函数Fig.9 Displacement response functions

图10 有限周期性Mindlin板中位移分布Fig.10 Distribution of transverse deflection in finite-unit-cell periodic Mindlin plate

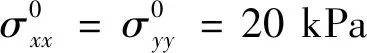
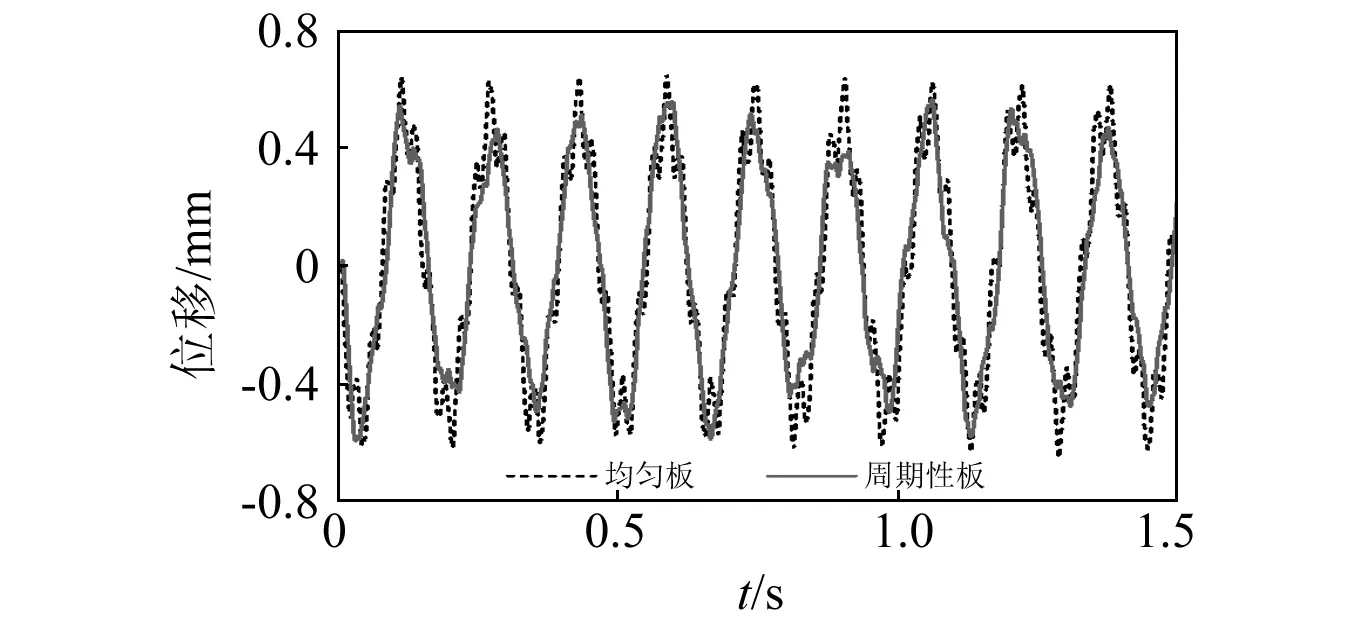
图11 无初应力时6.4 Hz激励作用下输出端的响应Fig.11 Dynamic responses of the output end under excitation of f=6.4 Hz without initial stress

图时6.4 Hz激励作用下输出端的响应Fig.12 Dynamic responses of the output end under excitation of

5 结 论

结合弱形式求积元法和周期性结构理论，本文提出了含初应力周期性局域共振Mindlin板衰减域及衰减系数计算方法，系统研究了初应力和几何参数对衰减域特性的影响，并与有限周期性局域共振Mindlin板的动力响应进行了对比验证。

研究结果表明，压初应力作用下衰减域的频率降低，衰减域内波的衰减程度降低；而拉初应力作用下衰减域的频率升高，衰减域内波的衰减程度增强。周期性局域共振Mindlin板的衰减域起始频率取决于散射体和包裹层组成的“振子系统”的共振频率。故随包裹层厚度和散射体尺寸的增大，衰减域起始频率降低。